
おはようございます!
昨日は【二項係数の漸化式】の証明に挑戦しました.3通りの方法で行ってみましたが,今朝はそのうちの1つをシェアさせていただきたいと思います.
さて,ここで「二項係数の漸化式」と呼んでいるのは,次の恒等式のことです:
nCkという表記は「異なるn個のものからk個を選ぶ方法の総数」を表します(☞注).nCk は, (1 + x)^n を二項展開したときの x^k の項の係数(二項係数)と一致するので同一視できます.
今回は次の "乗法公式” を用いて証明しましょう: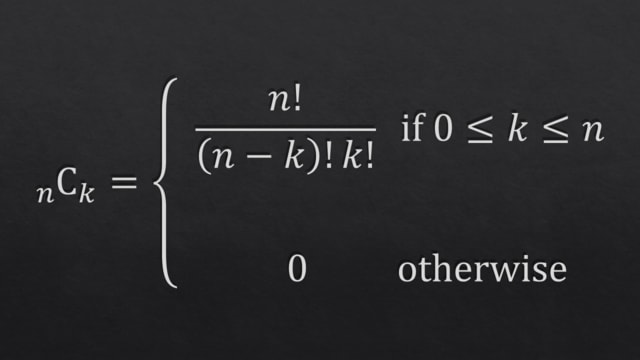
証明は次の通りとなります:
実は電車にガタゴト揺られながら証明していたのですが,夢中になりすぎていたあまり乗り過ごし,昨日は目的地までの終電を逃してしまいました(苦笑)
皆さま良い一日を.
注.S を濃度が n (< ∞) の集合とします.組合せ論では, S の部分集合のうち濃度が k であるものを「S の k-組合せ」と呼びます.S の k-組合せ全体から成る集合を P_k(S) (⊂ 冪集合 P(S)) と書くとき,この集合の濃度 |P_k(S)| を nCk と表記します.










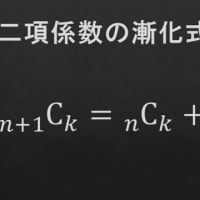




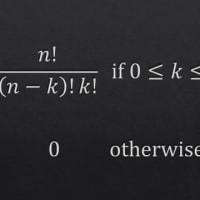


※コメント投稿者のブログIDはブログ作成者のみに通知されます