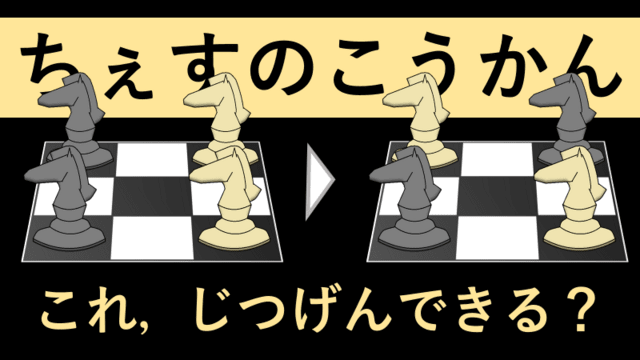
本日の数理パズルは,チェスの「ナイト(騎士)」が主役です.
【ルール 1】 ナイトというのは,将棋でいう「桂馬」のような動き方を四方に対して行うことができる駒です.

【ルール 2】 同じマスに複数の駒が存在することはできないものとします.

【問題】 上記のルール 1 および 2 を満たしながら,盤上の配置を次に示す (a) の状態から,(b) の状態に移動させることは可能でしょうか?

判りましたでしょうか...?
実はどんなに頑張っても,状態 (a) から状態 (b) に配置を変換することは決してできないのです.でも,どうしてでしょうか?
次のようにして不可能であることを,数学的に証明できます:
※今のところ,この動画のシリーズを視聴してくださる方のおよそ半数が英語話者なので,スライドのみ英語にて作成してみています.字幕(日本語・英語)を利用できます.
上手くお伝えできていると良いのですが...
動画内の証明で用いたような「頂点と辺から構成される構造」のことを数学では【グラフ】と呼びます(☞注).今回紹介した「チェス交換問題」(Chess swap problem)は,グラフの考え方を用いることで綺麗に解くことができる例の1つです.
グラフを用いた問題には直感的で面白いものがたくさんあるので,後の記事でもご紹介していければと思います.こうご期待!
注.数学では,(僕の知っている限り)「グラフ」という言葉を2つの全く異なる意味で用います.1つは,中学校の数学でも教わる関数のグラフです.関数 y = f(x) をプロットして得られる図形のことを指します.もう1つは,離散数学の分野でいうグラフです.頂点と辺からなる構造のことを指します(※この動画内で扱ったのはこちらです).
定義の仕方の流儀は色々ありますが,たとえば次のようにして両者を形式的に定義できます:
- 前者の「関数のグラフ」の定義
関数 f: X → Y に対して,Γ(f) := {(x, f(x)) | x ∈ X} のことを 【f のグラフ】という.
- 後者の「離散数学のグラフ」の定義 ※特に動画内で紹介した「無向グラフ」の定義
V を頂点の集合,また E :={{v, w} | v, w ∈ V} を辺の集合とする.このとき,組 (V, G) を【無向グラフ】という.
【出典】 今回紹介した問題は,次の教科書の第8章(Graph Algorithms)からの引用です.
Jones, N. C., & Pevzner, P. A. (2004). An Introduction to Bioinformatics Algorithms. MIT Press.
※図と類題は自作のものです.
















※コメント投稿者のブログIDはブログ作成者のみに通知されます