皆さんはふだん絵文字を使われますか?
近年 【Unicode絵文字】がますます充実し,さまざまな場面・環境で絵文字を使えるようになってきました.日本発祥の絵文字文化がいまや世界中でEmojiとして親しみ使われているというのは,なんだか面白いです.
※皆さんのお手元のブラウザでも今,👍(いいね)や🍎(リンゴ)といった絵文字を表示できていますでしょうか❓
さて,僕は果物の絵文字を使う機会が時々あるのですが,「へえ,こんな絵文字もあるのか!」と驚くことが多い一方で,「この果物もあればなあ...」と不足を感じてしまうこともあります.
そこで先日,Unicodeで用意されている果物の絵文字一覧を調べてみたのです.
想像はしていましたが,【Emoji化】されている果物の種類に大きく偏りがありました.(そしてこれは少し意外だったのですが)未だ日本で日常的に食べられている種に限られているようでした.
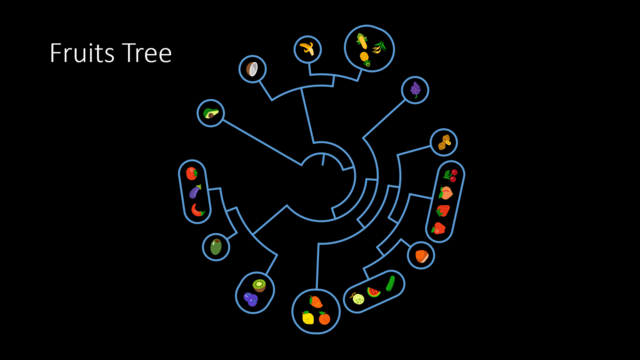
また戯れに “実” の部分を食用とする植物のEmojiを見つけられる限り集め,目レベルで系統樹を描いてみたところ,次のような『フルーツ・ツリー』が得られました(☞注):
※僕のアイコンに用いている画像です.
すべての種が【被子植物】と呼ばれるグループに属しています.思っていたよりもEmojiの種類が豊富だったので,大雑把ながらも被子植物全体の系統樹の形状をちゃんと見てとれます!
果物として人類に利用されている種は,そもそも被子植物の系統の中で非常に偏って分布しています.そのため,食用の植物だけをサンプルとして被子植物全体の系統を見てとることは本質的に困難なことではあります.しかし,「Emoji化されている種がいない」という理由によって描けていない「進化の枝」が多いのもなお事実です.
例えば次のような果物のEmojiがあると,もう少し賑やかな樹になって楽しそうです:ポポー(モクレン目)やドラゴンフルーツ(ナデシコ目),アケビ(キンポウゲ目),ザクロ・フェイジョア(フトモモ目),マンゴスチン・パッションフルーツ(キントラノオ目),ドリアン(アオイ目).
どうやらユニコード協会(The Unicode Consortium)のウェブサイト https://home.unicode.org/ で,一般のユーザーからも新しい絵文字の提案を募っているようです...!! 果物の絵文字が系統的にもっと多様になると良いな~😁
注.生物たちの進化の系譜(すなわち系統)を描いた図を【系統樹】といいます.過去どのように生物たちが進化してきたのか,という過程を人類は直接観察することができないため,どんな系統樹が「真の系譜」なのか正確には判りません.そのため,科学者によって推定される系統樹は結局のところ,いずれも仮説に過ぎません.
被子植物の系統に関する仮説は色々ありますが,上記の図を描くにあたってはDNA配列に基づいて推定されたAPG IVという仮説を用いました:
The Angiosperm Phylogeny Group. (2016). An update of the Angiosperm Phylogeny Group classification for the orders and families of flowering plants: APG IV. Botanical Journal of the Linnean Society, 181, 1–20. https://doi.org/10.1111/boj.12385
また系統樹を描くにあたっては,iTOL v6.1.2 (https://itol.embl.de/) というツールを用いました:
Letunic, I., & Bork, P. (2021). Interactive Tree Of Life (iTOL) v5: an online tool for phylogenetic tree display and annotation. Nucleic Acids Research, gkab301. https://doi.org/10.1093/nar/gkab301