知恵袋 https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q12226893717 より↓
【問1】図3(a)において
(a).コレクタ(バイアス)電流Icと、コレクタ、エミッタ間(バイアス)電圧VCEを求めよ!
但し、VBE=0.6V、IC≒IEとする
(b).スイッチSオン時の電圧増幅度|Av|を求めよ!
(c).スイッチSオフ時の電圧増幅度|Avf|を求めよ!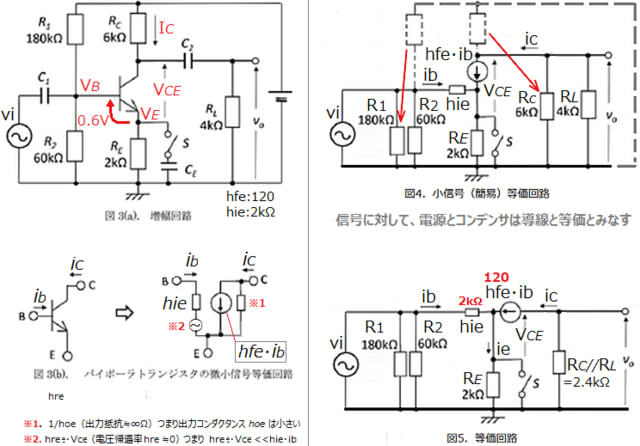
(※1、※2:hパラメーターの導出、YouTube動画)
答え:
(a).直流のIc=1.2mA , VCE=2.4V
(b).スイッチSオン時の|Av|=144
(c).スイッチSオフ時の|Avf|≒1.2
解説:
▶バイアス(直流)の考察
(a).図3(a)より、ベース(直流バイアス)電圧VBは
VB={R1/(R1+R2)}・Vcc={60k/(180k+60k)}×12V=3V
題意によりVBE=0.6Vなのでエミッタ(バイアス)電圧VE=VB-VBE=3ー0.6=2.4V
ゆえにエミッタ(バイアス)電流IE=VE/RE=2.4/2k=1.2mA
題意によりIE≒Icなので
∴ コレクタ(バイアス)電流Ic≒IE=1.2mA …(答え)
∴ コレクタ、エミッタ間(バイアス)電圧VCE=VccーVE-(Rc×Ic)≒12ー2.4-7.2=2.4V …(答え)
▶信号(交流)の考察
先ず、小信号(簡易)等価回路の考え方の基本:
電圧源は内部抵抗=0Ωなので信号波形への影響はないので電源は等価的に(ほぼ導線と同じ)とみなせる。
加えて、コンデンサのインピーダンスはkΩ単位の各抵抗に比べて充分に小さく、コンデンサのインピーダンスが回路に与える影響は小さくなる様な値を採用する事で(コンデンサは)ほぼ導線と同じとみなせる様になる。
つまり、コンデンサと直流電源は小信号(簡易)等価回路において「導線」に置き換えて回路図を描き直す。
(b).スイッチオン時:
小信号(簡易)等価回路の考え方:
(電圧源は内部抵抗=0Ωなので信号波形への影響はないので電源は等価的に導線と同じみなせる。加えて使用周波数の中間帯域に対するコンデンサのインピーダンス)はkΩ単位の各抵抗に比べて充分に小さくなる様な容量のものを採択する事で回路に与える影響は小さく無視できるもとして)
題意によりC1,C2,CE両端は短絡とみなせる。とされているので小信号(簡易)等価回路は図5の様になります。図5より
Vi=hie・ib=2k・ib
Vo=-{(Rc・RL)/(Rc+RL)}・hfe・ib
=-{(6k・4k)/(6k+4k)}・120・ib
=-288k・ib
∴ 電圧増幅度 |V(A)|=|Vo| / |vi| =288k・ib/2k・ib=144 …(答え)
(c).スイッチオフ時:図5より
Vi=hie・ib+RE・IE
=hie・ib+RE・(ib+hfe・ib)
=hie・ib+RE・(1+hfe)・ib
={hie+RE・(1+hfe)}・ib
≒RE・hfe・ib (等式なら={2k+2k・(1+120)}・ib=244k・ib)
=2k・120・ib
=240k・ib
(∵ 1<<hfe, hie<<RE・hfe)
Vo=-{(Rc・RL)/(Rc+RL)}・hfe・ib
=-{(6k・4k)/(6k+4k)}・120・ib
=-288k・ib
∴ 電圧増幅度 |V(Af)|=|Vo| / |vi| ≒288k・ib/240k・ib=1.2 …(答え)
等式なら≒288k/244k≒1.18≒1.2









