知恵袋 https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q11294321926
▶別解
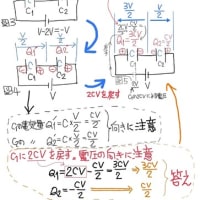
C1の電荷を空っぽにして計算し易くする為に、
C1の2CV[クーロン]を、一旦、等価電圧(2CV/C1=2V)へ置き換える(図2)
この時、C1,C2は(暫定的に)空っぽの状態 スイッチを閉じると電源は等価的にV−2V=−V (つまり逆向きの電圧V)になる。図4
図4の等価電圧VによりC1,C2に溜まる電荷量Q=CV/2 (図5)
等価電圧Vを元の2つの電圧に復元する(図6)
図6の等価電圧2V[V]を、C1へ戻す(図7)
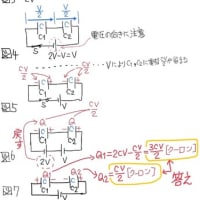
図7より
∴C1の電荷量Q1=2CV−CV/2=3CV/2 [クーロン] …(答え)
∴C2の電荷量Q2=CV/2 [クーロン] …(答え)

▶別解2
≫一旦、2CVを無視して考えたのですが
≫この考え方はなぜダメなのでしょうか?
↑
ダメではありませんよ、⭕です。 但し、必ず最後に2CVはC1の所へ戻してください。 あと、肝要なのは、C1の2CVを無視する代わりに、C1の電圧=2CV/C1=2Vを(この回路の場合は)電源=Vより引き算する必要があります。
なので結果的に(って云うか等価的に) 電源の電圧=V−2V=−V つまり電源の等価電圧は、逆方向のV(つまり−V)として考える必要があります。
要するに C1の電荷=2CVを、一旦、無視する代わりに、こう云う等価電源への変換が必要であり、最後に2CVの電荷をC1へ戻す。(←この考え方が肝要なのです)
▶別解(計算)
(下図:等価回路) C1の2CVを一旦、取り除きます。(でも、必ず、最後には戻してください)
C1,C2は空っぽの状態と考え(図2)、その合成容量はC/2なので(等価電源=−Vなので)各コンデンサの電圧は−V/2です。
だから各コンデンサに蓄えられる電気量(電荷量)は(公式よりQ=CVだから)図4より
C1の電気量Q1=C×(−V/2)=−CV/2
C2の電気量Q2=C×(−V/2)=−CV/2
(この時の電圧の向きを意識してください)
これのC1に(2CV)を(電圧の向きを考慮しながら)戻すと
C1の電気量Q1=2CV−CV/2=3CV/2
C2の電荷量Q2=−CV/2
ここで各コンデンサの電気量を大きさだけに着目すると電圧の方向は関係なく大きさ(絶対値)として
C1の電気量Q1=2CV−CV/2=3CV/2 …(答え)
C2の電荷量Q2=CV/2 …(答え)
(図5)



















※コメント投稿者のブログIDはブログ作成者のみに通知されます