コンデンサつなぎ替え

▶知恵袋:https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1330703652

▶コンデンサつなぎ替え

(1).

(a)、題意よりコンデンサは充電完了しているのでC1,C2に電流は流れずC1,C2は接続されていない状態と同じなのでX,YZの電位はE1,E2,R1,R2,R3のみで計算できX,Y,Zの電位Vx,Vy,Vzを考察すると（分圧の法則より）

Vx=6.0×(20+30)/(10+20+30)=5.0v

Vy=6.0×30/(10+20+30)=3.0v

Vz=1.5v

∴XY間の電位差Vxy=Vx−Vy=5.0−3.0=2.0v　…(答え)

∴YZ間の電位差=Vy−Vz=3.0−1.5=1.5v　…(答え)

この時、XZ間の電位差Vxz=2.0+1.5=3.5v　…①

 

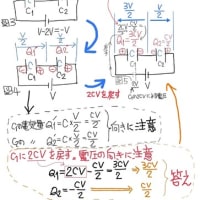
(b)、コンデンサに溜まる電気量は公式よりQ=CVなので

C1に溜まる電気量Q1’=C1Vxy=2.5×2.0=5.0μC　…(答え)

C2に溜まる電気量Q2’=C2Vyz=5.0×1.5=7.5μC　…(答え)

つまり

①式はQ1’/C1+Q2’/C2=5.0/2.5+7.5/5.0=3.5v　…②

と云う事です。

 

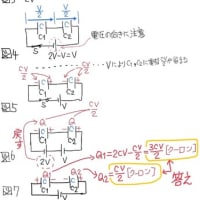
(c)、

C1,C2のP側の電気量の合計=−5.0+7.5=2.5μC　…(答え)

 

(2).

(a)、S1開き、S2閉じ十分時間経過するとC1,C2に電流は流れずC1,C2は接続されていない状態と同じなので節点Pにおいてキルヒホッフの第1法則より

I2+I3+I4=0　…(答え)

が成立し、Pの電位Vpはミルマンの定理より

Vp={6.0/(10+20)+1.5/10}×1/{1/(10+20)+1/30+1/10}

=(6.0/30+4.5/30)×1/(1/30+1/30+3/30)

=(10.5/30)×(30/5)

=10.5/5

=21/10

=2.1v

この電位2.1vを共通としてキルヒホッフの第2法則より

2.1=6.0−(10+20)I2　→∴I2=(6.0−2.1)/30=0.13A　…(答え)

2.1=−30I3　→∴I3=−2.1/30=−0.07A　…(答え)

2.1=1.5−10I4　→∴I4=(1.5−2.1)/10=−0.06A　…(答え)

 

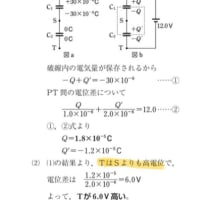
(b)、XZ間の電位差Vxz=Vx’−Vz’として

Xの電位Vx’=Vp+20I2=2.1+20×0.13=2.1+2.6=4.7v

又はVx’=6.0−10I2=6.0−10×0.13=6.0−1.3=4.7v

Zの電位Vz’=1.5v

∴XZ間の電位差Vxz’=4.7−1.5=3.2v　…(答え)

つまりVxz’=(C1の電圧)+(C2の電圧)=3.2v

でもあると云う事です。

 

(c)、

▶別解

XZ間の電位差Vxzは、始めの(1).(a)項の時はVxz=3.5vあったものが(2).(b)項の時はVxz’=3.2vに低下しているのでC1,C2より電荷Q’が流出して電圧が0.3v低下したと云う事なので流出したQ’とキルヒホッフの第2法則より

3.5−3.2=Q’/C1+Q’/C2=Q’/2.5+Q’/5.0=3Q’/5.0

流出したQ’を求めると

Q’=0.3×5.0/3=0.5μC

この0.5μCがC1,C2から流出してVxz’=3.2vになったので

キルヒホッフの第2法則より

3.2=Q1/C1+Q2/C2　…(答え)

=(Q1’−Q’)/C1+(Q2’−Q’)/C2

=(5.0−0.5)/2.5+(7.5−0.5)/5.0 

=4.5/2.5+7.0/5.0

∴Q1=4.5μC　…(答え)

∴Q2=7.0μC　…(答え)

 

▶解答：…未…