なんとか、何かしら日記サイトに登録することがかないました。
どうしていいかわからず、いろんなサイトにメールアドレス登録したはいいものの、結局月額○○円だったり、なんかよくわからなかったり(これが一番)……いろんな方面に自分のメールアドレスばら撒いただけで終わりました。
なんとかありつけたこの場所で駄文をだらだらしていこうと思います。その時書きたいものについて書くので、話題が偏ったり、「え?なにそれ?」みたいなものが多くなったり、文量がかなり増えたり少なくなったりしそうです。本当すみません、ご了承くださいませ。
では、今日の書きたいことから。
この前Twitterで1964年第6回IMOソビエト大会の問題を見ました(数学オリンピックです)。
「17人が互いに(どの人も他の全員と)手紙で文通をしている。その手紙では、3つの異なった話題だけが議論されている。どの2人の文通相手についても、いつも手紙の話題は同じ1つのことである。すると、ある3人を適当に選べば、この3人は同一の話題について文通していることを
証明せよ。」
文通、時代ですよね。1964年はもう60年弱も昔の話……東京オリンピックの年……
何か感慨深いものが湧いてくるかなと思って書いてみましたが別になんもなかったです。駄文。
17人が文通してますとなって「何の話題について話しているんだろう?」って考える人は感受性豊かだなぁって心底思います。それくらい心が豊かになりたい。僕は2秒で「話題A,B,C」です。
問題は、「17人のうちのとある3人で、その間の3か所の文通は全て同じ内容であるような人たちがいますよ」ということを示しなさい!と言っているのですね。
どう考えていくのがいいのかなってなった時に、まずは具体的に実験してみよう!というのは、数学の問題を解く上では大事です。なんなら数学じゃなくても、実験でどうなるのか確かめてみる事は重要なことなんじゃないですか?プログラミングは実行してみてそれが命令として適切か、はたまたエラーを起こすものなのかが分かるものと思います。知らないのでこれ以上は深入りしません。
17人から1人抜いてきて、①さんとしましょう。①さんは他の16人と何かしら文通しています。話題Aについて話している相手を考えてみましょう……しかし、話題A,B,Cと言いましたが、①さんはこの3種類全部を話しているとは限らないんですよね。もしかしたらAのことは話してないかもしれないし、逆に全員とAでしか話していないかもしれない。「Aについて話している相手の人数が0〜16人いずれかがわからない」。0〜16で全部試すのか!?具体的に考えてみようとしたところで、ここが最初の考えにくいポイントなのかなと思います。
ここで、一工夫をいれてみました。
A,B,Cの話題で16人と話すのですから、
A+B+C=16
ですよね(雑)こんな適当な立式勝手にしちゃダメですよ!A,B,Cは数字じゃないんですから!!
Aが小さければB,Cはある程度大きく、Aが大きければB,Cはある程度小さくなるという傾向にあります。なぜなら3つの和が16で固定されているので。話される数は0〜16ですが、一番話される話題は少なくとも4,5,6?ぐらいは話されそうですよね。
数学的には、話題A,B,Cに「話されている数が少なくない順にA,B,Cとする」など、数的関係を導入します。すると、
A≧B≧C
の不等式が出来上がり、
16=A+B+C≦A+A+A=3A
A≧16/3>5
すなわちA≧6(上記の通り立式が雑)
と、一番話されている話題の数が6以上だと計算できます。
この、「最低6人と話されている話題A」について考えるとなると、やりやすくなります。「まず①さんが他の6人とAについて話しているとして…」という実験ができますからね。
では、①さんが話題Aを話している6人について考えてみましょう。この6人で文通を行う場合、6C2=15(ペア)が考えられます。6C2が何のことかわからない人は、6人を②〜⑦とでも置いて、2人組のペアを全部書き出してみましょう。
(2,○) [○=3〜7の5パターン]
(3,○) [○=4〜7の4パターン]
(4,○) [○=5〜7の3パターン]
(5,○) [○=6,7の2パターン]
(6,7)
の1+2+3+4+5=15ペアです。書き出すにしても、同じものがダブらないように数える工夫が必要です。上ではペアを(△,○)と表記する際、必ず△<○となるように注意しています。△>○のペアがあると、ダブってしまいます(例えば(6,4)などは3段目の(4,6)と同じ)。
15ペアのうち、1ペアでも話題Aについて話していれば、題意は満たされます。なぜなら、①さんとそのペアの3人の間では話題Aのみが共有されていますから。
では、考えるべきは「15ペアすべてがAを話していない」ケースです。6人からなる15ペアが残りの2つの話題B,Cについて話している時を考えましょう。
またこの6人の中から具体的に②さんを抜いてきます。②さんは他の5人とB,Cの話題をしていますね。また実験です。話題Bについて話している相手を考えてみましょう……同じく、Bを話している相手は0〜5人で変動します。さっきのAの時ほどしんどくはないですね。0〜16で動かすより、0〜5のほうが気持ちが楽です。0〜5くらい、全部試してみることは十分可能です。
Bの話題0人の時
Bの話題1人の時
………
やる人は頑張ってください!
僕はここでも、先と同じように「②さんが話している話題で、少なくない方をB',もう一方をC'」と設定し直し、
5=B'+C'≦B'+B'=2B'
B'≧5/2>2
すなわちB'≧3
から、②さんが少なくとも3人とお話しているB'を追いかけたいと思います。
この3人で文通を行う場合、3C2=3(ペア)が考えられます。3C2が何のことかわからない人は、頑張って3人でできるペアを全部書き出してください。多分3ペアしかないです。
この3ペアのうち、1ペアでもB'の話をしていれば、題意は満たされます。なぜなら、②さんとそのペアの3人の間では、話題Aのみが共有されていますから。
では、考えるべきは「3ペアがすべてB'を話していないケース」です。3ペアがすべてC'について話している場合を……気づかれましたか…。
まずある人について、1番少なくない数話されている話題について考える。それは必ず6人以上と共有されているので、その中から6人を選んで考える。(中略)そして、その6人の中から1人を選んで、その人について1番少なくない数話されている話題について考える。それは必ず3人以上と共有されているので、その中から3人を選んで考える。(省略)
こんな流れですね。個人的には、話されている話題の数について大小関係の導入が、具体的に考えていく上でとっても重要だったと思える点です。整数問題とかでも大小関係の導入はよくありますが、こんなところにも生きてしまったんですねぇと感嘆の声です。
では、本日の文章を締め括ります。ありがとうございました。最後に、発音アクセントのお勉強です。
かなう(カナ\ウ)
ばら撒く(バラマ\ク)
偏る(カタヨ\ル)
2人(フタリ\)
不等式(フト\ーシキ)
出来上がる(デキアガルー)
行う(オコナウー)
置く(オクー)
数える(カゾエ\ル)
気づく(キヅ\ク)
選ぶ(エラ\ブ)













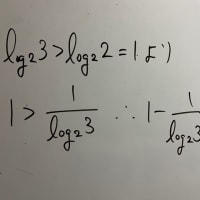
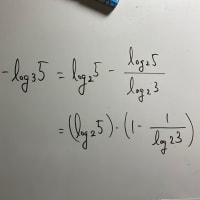
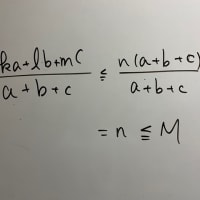
※コメント投稿者のブログIDはブログ作成者のみに通知されます