宇宙際タイヒミュラー理論についての覚え書き(2)

目次
はじめに
表1. [KF01]と[IUT2ABC05]-[IUT2ABC07] 間での用語や説明との対応
表2. [KF01]に出てくる数式（と数式扱いの文）の本記事での参照時の記号
表3.本記事での説明と関連する [KF01]の図（表1を参照）
1. 多輻的 (multiradial) アルゴリズム
2. 既存の数学と IUT 理論
2.1 数論幾何学と IUT 理論
2.2 IUT 理論における局所と大域
2.3 モデル理論とIUT理論
2.4 類体論とIUT理論
3. q-標対象 (q pilot object) とΘ標対象 (Θ pilot object)

はじめに^

用語、参照文献の記号は「宇宙際タイヒミュラー理論についての覚え書き(1)」と共通。
本ブログの関連記事を参照する際の記号を決めておく。
[IUT2ABC01]:ABC予想は確かに証明されていると信じられる理由
[IUT2ABC02]:ABC予想は確かに証明されていると信じられる理由（２）
[IUT2ABC03]:読書ノート：ＡＢＣ予想入門（黒川 信重/小山 信也【著】）
[IUT2ABC04]:読書日記：黒川信重，小島寛之の「21世紀の新しい数学」
[IUT2ABC05]:読書ノート:「宇宙と宇宙をつなぐ数学 IUT理論の衝撃」
[IUT2ABC06]:宇宙際タイヒミュラー理論についての覚え書き(1)（前記事）
[IUT2ABC07]:宇宙際タイヒミュラー理論についての覚え書き(2)（本記事）

書籍[KF01]（↑「宇宙と宇宙…」）に言及する際の便宜上の事を記しておく。

表1. [KF01]と[IUT2ABC05]-[IUT2ABC07] 間での用語や説明との対応^
[KF01] での用語 ↔ [IUT2ABC05]-[IUT2ABC07] での用語や説明
「舞台」(1) ↔ 圏
「舞台」(2) ↔ ホッジ劇場
「入れ子宇宙」(1)↔ 「x∈x」であるかのような仮想的集合
「入れ子宇宙」(2)↔ 対数テータ格子
「対称性」(1)↔ 群、群の作用
「対称性」(2)↔ エタール的対象
「モノ」↔ フロベニウス的対象
「対称性による復元」↔ 単遠アーベル幾何での復元
「対称性通信」↔ 単遠アーベル的輸送
「ピースをはめる」 ↔ 多輻的アルゴリズム（による計算）
「計算の伝達」＋「精密な同期」 ↔ 多輻的アルゴリズム（による計算）

表2. [KF01]に出てくる数式（と数式扱いの文）の本記事での参照時の記号^
(a) degΘ "=" degq (p.198)
(a)'（図5-7 の中の式) degΘ "=" degq (p.198)
(b) degΘ ≤ degq + c (p.200)
(b)' 同上 (p.269)
(c) q (p.270)
(d) Nlog(q) ≒log(q) (p.271)
(e) Nlog(q)
(f) log(q)/(N-1) < c (p.272)<br />(g) （図8-1 の中の式) q_A ≅ (q_B)^N (p.273)
(h) (q_B)^N ≅ q_A (p.275)
(i) (q_B)^N ≅ (q_A)^N (p.275)
(j) (q_A)^N と q_A は「ほぼ等しい」 (p.276)
(h)'（図8-2 の中の式) (q_B)^N ≅ q_A (p.277)
(i)'（図8-2 の中の式) (q_B)^N ≅ (q_A)^N (p.277)
(k) Nlog(q_A) ≒log(q_A) (p.281)
(l) Nlog(q_A)
(b)" degΘ ≤ degq + c (p.282)
(m) Ndegq (p.283)
(n) degq (p.283)

表3.本記事での説明と関連する [KF01]の図（表1を参照）^
図3-2 タイヒミュラー理論のイメージ (p.121)
図5-3 IUT的なジグソーパズル (p.184)
図5-4 映画の役を演じている現実世界の女優 (左) と映画の中の女優 (右) (p.190)
図5-5 入れ子になった「舞台」 (p.193)
図5-6 異なる舞台のピースを「はめる」 (p.195)
図5-7 異なるサイズの「かけ算」というピースをはめる (p.199)
図6-4 対称性による復元 (p.213)
図6-7 対称性通信の原理 (p.218)
図8-1 異なる数学の舞台のピースをはめる (p.273)
図8-2 入れ子舞台と対称性通信 (p.277)
図8-3 IUT理論がやっていること。出典… (p.289)

疑問:[KF01]p.280 ll.8-9 「点付き楕円曲線」は「一点抜き楕円曲線」の誤記では？
∵[HY02]（「続・宇宙際 teichmüller理論入門」）p.3 §1 の下記 X を指すのでは？
「X は E からその原点を取り除くことで得られる F 上の ((1, 1) 型) 双曲的曲線」

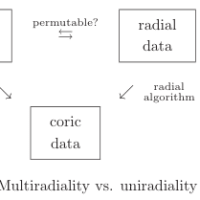
1. 多輻的 (multiradial) アルゴリズム^

[IUT2ABC05]では[YG01]での説明を引用。ここでは他の文献を参照し、図や説明を補足する 。
単解構造を共有する複数の異なる正則構造（が属する圏／宇宙）の間で共有可能な出力が
得られる（i.e. テータリンクと両立する）アルゴリズムは、次の (a),(b)２種類がある。
(a) コア的 (coric) アルゴリズム: そもそも、計算過程に単解構造の要素しか出てこない。
(b) 多輻的アルゴリズム: 正則構造の要素を使うが、結果は正則構造の選択に依存しない。
上記２つは、異なる宇宙で同時並行的に well-defined であるアルゴリズムとも言える。
cf.
(c) 単輻的 (uniradial) アルゴリズムの結果は、正則構造が異なる圏／宇宙と共有不可能。
これらのアルゴリズム (a)-(c) の参考文献での説明で、下記の用語 (A), (B) も使われる。

(A) 輻的データ (radial data) : 大半の文脈で「正則構造に属するデータ」の意味になる。
(B) コア的データ (coric data): 大半の文脈で「単解構造に属するデータ」の意味になる。

e.g. [HY01]p.25では、下記のように (a)-(c) が説明されている。
(a) コア的データにのみ依存するとき, アルゴリズム Ψ は コア的アルゴリズム
(b) 多輻的アルゴリズムとは, “コア的データの同一視/共有”と両立する形で
“同時実行可能” なアルゴリズム
(c) 単輻的アルゴリズムとは, (“多” 数の上部 “輻” 的データに同時に適用できない)
各々“単”一の特定の“輻”的データのもとでのみ意味を持つ。

[MS03]p.52では、(b) と (c) の違いを Fig3.1 で図示している。[MS03]p.55 Fig3.2 では、
[IUT2ABC06]でも引用した「実数体２つの直積に複素数の正則構造を入れた場合」における
正則構造に属する演算を単輻的アルゴリズムの例として挙げている。


一般に群作用の軌道 (orbit) は、（定義から明らかに）その作用に対して不変であることに注意。
∴（複数の正則構造に共有される）単解構造の自己同型群を、正則構造に属する輻的データに
作用させて軌道を求めるアルゴリズムは、多輻的（下図: [MS03]p.56 Fig.3.3）。


[HY01]p.26の図も、[MS03]pp.52-56 での説明と同じ例を示している。


上図は [HY01]p.26 単輻的アルゴリズムの例 ([MS03]p.55 Fig3.2 相当)


上図は [HY01]p.26 多輻的アルゴリズムの例 ([MS03]p.56 Fig3.3 相当)

「輻」の字は、自転車の車輪などにあるスポークの意味(cf. [FI02]p.12、[MS03]p.33)で、
車輪全体が単解構造を共有する複数の異なる正則構造、個々の正則構造が一本のスポークの
イメージからの命名。[MS02]p.15の図 (Fig2.2) は、このイメージを意識している。



[IUT2ABC05] で言及した{厳密／フォーマル}な圏論的定義では、まず前述の２種類のデータ
(A), (B) それぞれの圏を所与として、２つの圏の間の関手としてアルゴリズムを見たとき、
「充満 (full)」であれば、多輻的、そうでなければ単輻的（[MS03]pp.50-51 にも同じ説明）。
[MS03]p.31 で「充満性 (fullness)」は「複数の輻的データの集りからの並列転送の存在」に
相当すると注意されている。

2. 既存の数学と IUT 理論^

本節の内容は、主に[FI01]と[FI02]を参考にした。なお、フェセンコは、ここでは述べて
いない一元体 F_1 関連の数学との関係などにも言及している。

2.1 数論幾何学と IUT 理論^

幾何学的な手法で整数論を研究するのが数論幾何学とすれば、当然、IUT 理論⊂数論幾何学。
しかし、WikiPedia での数論幾何学の説明は、執筆者が＊うっかり＊^^; スキーム論を前提に
してしまっている。IUT理論はスキーム論の枠組に収まらない。∴IUT理論⊄数論幾何学
ということになる。^^;少なくとも「IUT 理論は数論幾何学における大変革」とは言えよう。
https://ja.wikipedia.org/wiki/数論幾何学
「数論の問題を解くために代数幾何の道具を用い、初等的でない定義を使う。スキーム論の
出現後、数論幾何は整数環 Z のスペクトル上の有限型のアレクサンドル・グロタンディークの
スキームの研究として合理的に定義できよう」

スキーム論は可換環論の幾何学的な言い換えという見方もできる。可換環論は線型代数を
含むから？か、群そのものより群の表現の方が「相性が良い」らしい。類体論をガロア群が
非可換な場合に拡張する研究（非可換類体論）の定式化（ラングランズ予想）は、ガロア群
自体ではなく、ガロア群の表現／ガロア表現を主に考察するという発想の転換により成功
したと、黒川信重が著書「絶対数学の世界」で述べている（p.121とp.145）。

一方、IUT 理論の基礎である遠アーベル幾何学では、「純群論的な復元アルゴリズム」の
構成が鍵になる。IUT理論への応用が可能なのは、「復元アルゴリズムが乗法モノイドへの
群作用にのみ依存し、基礎体の加法には依存しない」から。
ところで、加法を保つ写像⊃線型写像⊃（群の）表現（の値域）。
i.e. 表現論は一つの宇宙の中に閉じてしか意味付けできない（単輻的な）ので、少なくとも
宇宙間通信（多輻的アルゴリズム）には使えない。∴IUT 理論では従来の数論幾何学の中ほど
には表現論の「神通力」が発揮されない（「F_1 上の表現論」が出現すれば話は別になるかも）。
https://ivanfesenko.org/wp-content/uploads//Q/C1/q6m.pdf p.20
"Unlike the Langlands correspondences which rather involve the use of
linear objects, one has to use the full arithmetic fundamental groups
in anabelian geometry and IUT."

なお、スキーム論で「素イデアルは＊厳密な意味で＊ある「幾何的な空間（位相空間）」の
点と見なせる」ようになる前から、代数的整数の構造と解析学や幾何学の対象の間に様々な
類似性があるという認識は、かなり早い時期から、されていたようだ。
https://ja.wikipedia.org/wiki/大域体
「数体とリーマン面の類似という考え方は、19世紀のリヒャルト・デーデキント
(Richard Dedekind) やハインリッヒ・ウェーバー (Heinrich M. Weber) まで遡る」
数学セミナー別冊「モジュライの楽しみ」pp.113-120 「リーマン面（上野健爾）」p.119
「基本群と不分岐被覆の関係はヒルベルトが類体論を構想する際のモデルになった」
# e.g、拡大体での素イデアル P が基礎体の素イデアル p を含むとき「P は p の上にある」
# と言われるのは、この関係と「被覆空間」概念との類似性のため、素イデアルの「分岐」は
# 解析接続で生ずる複素関数の「分岐」との類似性からの命名。
「素点」の名称は、「（リーマン面の）代数関数体」と「数体（ここでは有理数体とする）」
に対して、各々 (1), (2) のように定義した V_P(f) と V_p(q) （両者に共通の性質を抽象化して
「付値」という概念が定義される）における点 P と素数 p の対応に由来。
(1) リーマン面上の代数関数 f に対し、「点 P を原点とする局所座標 z での表示」に
応じて、g を g(z)≠0 である関数とし、次のように定めた V_P(f)。
f(z)=g(z)×z^m → V_P(f) = m ; f(z) = g(z)×z^(-m) → V_P(f) = -m ; それ以外はV_P(f) = 0
(2) 有理数の既約分数表示 q=a/b と素数 p について、r, s を p で割れない整数として、
次のように定めた V_p(q)。
a = r×p^m → V_p(q) = m ; b = s×p^m → V_p(q) = -m ; それ以外はV_p(q) = 0

IUT理論は、古典タイヒミュラー理論や多様体の変形理論との類似性でも、数論幾何学の
中では異色の存在という印象があるが、数論の初期から注目されていた方面の幾何学との
類似性を厳密に定式化したという見方もできる。∵こうした側面は、望月の業績の特徴。
典型的な事例の一つは、望月の初期の代表的業績である「p進遠アーベル幾何の確立」。

遠アーベル幾何学の創案者のグロタンディークが「遠アーベル的な現象」は大域体に固有と
考えていたので、望月以前の遠アーベル幾何学の研究は、全て大域体に関するものだった。
ところが、望月は p進体という局所体の上で、それまでの遠アーベル幾何よりも完成度の
高い理論を構築した。望月が道標としたのは、「ケーベの一意化定理」というリーマン面に
関する定理が、＊局所体である複素数体における遠アーベル的な現象と解釈できる＊という、
望月が指摘するまで誰も気付かなかった事実。古典的な幾何学との類似性に着目することは、
以後も一貫した望月の研究方針の中核。望月が指導を担当する学生に要求する予備知識からも、
その事が伺える。

cf. 大半の数学者には、実数体や複素数体と p進体の間の違いの方に目が行きやすい事は、
例えば WikiPedia での局所体の説明から伺える。∴類似性を研究方針の中核に据えている
望月の発想は、望月の業績を十分に知らない数学者には「分かりにくい」のかも知れない。
https://ja.wikipedia.org/wiki/局所体
「実数体(複素数体)と p進体または1変数ベキ級数体とでは性質の異なる部分が多いので、
ここでは当初の定義通り、特に断らない限り局所体といった場合、実数体や複素数体は
含まれないとする」

2.2 IUT 理論における局所と大域^

[KF01]pp.283-286「局所と大域」とpp.286-290「精密な同期」の二節での話は、[KF01]の
説明中で最も分かりにくい。特に p.287 中ほどの「全部ではないが、それでも無限個の
素点を束ねて議論することを…」以下の説明は、筆者の理解との整合性がよくない。^^;

筆者の（大雑把な^^;）理解では、IUT理論においても「全ての素点で考える」という条件は、
満たされている。ただし、条件の満たし方が「従来のやり方からすれば、ちょっと常識はずれ」
（p.287最終行）だという説明ならば、違和感がない。つまり、筆者の認識は以下の (1)+(2)。
(1) 「従来のやり方」の典型、例えば「楕円曲線のゼータ関数でのオイラー積の定義」では、
「悪い素点／素数の項を、良い素点／素数の項と多少は違う形にする」程度で条件を満たす。
(2) IUT理論では、実質的意味があるのは悪い素点／素数関連部分だけで、良い素点／素数や
無限素点関連部は、「トリビアル」で「形式的」（オイラー積のイメージで言えば、定数 1
としておくような事）。

「悪い素点／素数」は、基礎体を固定した一つの（一点抜き）楕円曲線に対しては、有限個の
はず…なので、p.287中ほど「全部ではない」の後に「それでも無限個」と続けている箇所の
意図が、よく分からない（∵筆者の理解では「形式的には全部、実質的には有限個」なので）。
「宇宙が無限個必要であること」から、「（局所大域原理での）素点も無限個」だと述べた
という解釈も考えて見たが、無理があるように感じる。

なお、「局所類体論」がIUT 理論における（局所的な）Kummer 同型で「円分剛性」を保証する
役割を担っているという説明が、[HY01]p.10に出てくる。

最後になるが、「単輻的」を局所的、「コア的」を大域的に対応させると、前節の主題である
多輻的アルゴリズムという概念は、ある意味で局所大域原理に相当するようにも思われる事を
つけ加えておきたい。冒頭で言及した[KF01]での記述の意図も、この論点の提示かも知れない。

2.3 モデル理論とIUT理論^

加藤文元は IUT 4論文の公表前に、望月と「IUT 理論に真っ先に反応するのは、数学基礎論の
専門家かも知れない」と話したことがあるそうだ。この予想は的中した。[FI01] によれば、
"Model theorists were the first to react to IUT." ということで、model theorist とは
「モデル理論 (model theory)」の専門家のこと。そして、モデル理論⊂数学基礎論。

モデル理論とその周辺 坪井明人(筑波大学数理物質科学研究科)
「モデル理論は、数理論理学あるいは数学基礎論とよばれる分野のなかの一つである。
大ざっぱに言えば、数学的構造の一般論である。興味を持っている数学的構造を直接に
研究せず、その構造の間接的な性質に注目して議論をすることは、数学の研究上では
頻繁にあることだが、モデル理論ではそれが主要な方法論となる」

モデル理論は「見るからに「数学の基礎」や「論理学」の問題」だけでなく「一般的な
数学（e.g.「代数学」や「幾何学」）の問題」も研究対象」としている。つまり、問題を
＊モデル理論を道具として使って＊研究する。例えば、「モデル理論的な幾何学」ないし
「幾何学的モデル理論」と呼ばれる研究分野もある。この分野を紹介する「初歩的な例」
として、代数幾何の基本的な命題の一つ「ヒルベルトの零点定理」をモデル理論を応用
して証明して見せている教科書があったりする。「初歩的な例」なので、準備に必要な
モデル理論の概念は少なく、代数幾何の教科書にある普通の集合論的な証明と比較して、
少なくとも同等程度には簡潔。しかし、対象とする集合自体の性質を考察するのではなく、
「その集合を規定する公理に基づく理論が持つ論理学的な性質」を考察することで結論に
至るので「モデル理論的考察が威力を発揮する問題があり得る」事の説明にはなっている。

[FI01] は、モデル理論の観点から IUT が注目された理由として (1),(2) を挙げている。
(1) "Some of the reconstruction theorems may be understood in terms of a logical
interpretation. The concept of multiradiality may be understood in terms of
definability".
(2) "It is possible to imagine a certain model of theoretic mono-abelian geometry."
↑
(1) は「復元に関する定理が数理論理学用語での解釈が（興味深い可能性として）ありそう。
（例えば）多輻的であることは数理論理学用語での「定義可能性」として理解できそう。」と
いう話。(2) は単遠アーベル幾何を「（モデル理論用語での）理論」としての、「モデル」を
（興味深い可能性として）考えられそうだという話のようだ。

[FI02] p.24 に「モデル理論的な観点から見た IUT 理論」とでも題すべき内容の説明がある。
次のように「一般的なモデル理論での方法論」と対比させている。
(a) （幾何学への応用での）一般的なモデル理論での方法論では、（モデル理論の観点から）
２つの異なる理論（i.e. 前提とする公理群には違う部分がある）T と T' 間に「特定の形の
命題については共通に成立する」条件を見い出し、一方の理論（例えば T'）では証明困難な
特定の形の命題を、同じ形の命題が比較的容易に証明可能な理論 T を利用して証明する。
つまり、「異なるが共通の性質を持つモデル」が、理論（公理群）の違いにより形成される。
# 以下の例は、幾何学への応用される場合とは違い主に「理論的興味」から考えられたモデル。
# 例0: T =「ペアノの自然数論の公理系」、T' =「算術の超準モデル」（非可算集合のモデルもある！）
# より一般に、一階述語論理に基づく理論では、「レーヴェンハイム-スコーレムの定理」により、
#「無限集合の濃度」は規定されない。しかも、「ほとんどの数学理論は一階述語論理で記述可能」。
# ということで、例えば、一階述語論理で記述可能な範囲の実数論には「可算モデル」が存在し得る。
# 一階述語論理では「ある性質の「全ての」無限列」は扱わないので、対角線論法からの矛盾はない。
# 例1: T = （↓普通の）実数論の公理系、T' = 「超準解析」の公理系（無限小や無限大も数扱い！）
# 例2: T = ZFC 集合論前提の実数論の公理系、T' = 「ソロヴェイモデル（関数は全て可測）」
(b) IUT 理論での異なる宇宙にある対象に関する理論は、前提とする公理群は＊全く同じ＊。
つまり、T = T' だが、宇宙間での対応関係によって、宇宙ごとに「異なるモデル」になる。
# i.e. IUT 理論での「モデルとして異なる」は「数論的図形として形が違う／歪みがある」の言い換え。
「異なる宇宙（＝異なるモデル）でも共通に成立する命題」を利用する点は (a) と共通だが、
狙いが異なり、一つの宇宙（＝一つのモデル）の中では証明困難な命題を証明する。例えば、
下図（IUT 4論文中の第３論文の図 I.8）での -deg(q) の計算手順が宇宙間で共通（i.e.
「多輻的」）であることに言及している。


2.4 類体論とIUT理論^

まず類体論の概要説明は、下記（日本語 の）WikiPedia エントリ参照。
https://ja.wikipedia.org/wiki/類体論

宇宙際タイヒミュラー理論の日本語 WikiPedia での説明は、イヴァン・フェセンコが講演用
資料 (i),(ii) で「IU幾何を遠アーベル幾何から派生した新たな類体論に位置付けている」と
している。実は (i),(ii) では、そもそも遠アーベル幾何自体を類体論の発展形の一つだと
していて（ここまで上記の類体論の WikiPedia 説明と同じ）IUT 理論は、遠アーベル幾何
から派生した理論として、やはり類体論の一種という説明になっている。
(i) https://ivanfesenko.org/wp-content/uploads/2021/11/232.pdf
(ii) https://ivanfesenko.org/wp-content/uploads/2021/11/hat.pdf
# 先に 2.2 で述べた「「局所類体論」が IUT 理論の証明で使われる」事とは全く別の話。

上記２文書で「類体論」として一括りにされている理論のうち、もともとの「類体論」と
「高次（元）類体論」は、定式化や主要な命題の雰囲気が比較的似た印象だが、その他の
理論は、筆者の主観では、元々の類体論とは＊かなり見かけが違う＊印象。列挙された
「類体論」全ての共通点としては、「ある種の「体」の「拡大」と、その「ガロア群」の
関係を扱っている」事くらいしか、筆者には指摘できない。^^;

ラングランズ予想（上記２文書では「Langlands Correspondence|LC|ラングランズ対応」と
表記され、前記 WikiPedia では「ラングランズ・プログラム」と表記されている）。LC
という＊フェセンコの文書にある短い略語＊を以下で使用する。
LC を「非可換類体論」の定式化だとする文献が多い印象（例えば、黒川信重や加藤和也の
一般向け解説書）はあるし、Wikipedia にもそうある。
しかし、遠アーベル幾何は、ガロア群自体と作用する「体」との関係を扱うという点が
元々の類体論と共通なので、表現を介した関係を扱う LC 的「非可換類体論」とは別の、
遠アーベル幾何的「非可換類体論」があるということで、ひとまず納得はできる。

フェセンコは、IUT 理論に単体の遠アーベル幾何にはない＊元々の類体論との共通点＊が
いくつかあると述べている。筆者にとって比較的分かりやすかったのは「曲線の等分点」
という特殊値に着目する点が共通だという論点。i.e.
(1) 元々の類体論では「「ガロア群が可換」な拡大体は1 の巾根 i.e. 単位円の等分点を
基礎体に添加して得られる」という命題が、理論形成に際して重要な役割を果した。
(2) IUT 理論では、素数 l に対し（一点抜き）楕円曲線の「l 等分点」をテータリンクの
両端で値を共有可能にする「多輻的アルゴリズム」の構成に際し、「体」の加法構造を
復元するために使用する（i.e. 次節で言及する Θ標対象 の構成に使用される）。

3. q-標対象 (q pilot object) とΘ標対象 (Θ pilot object)^

IUT 理論の主定理 3.11 は、表題の両対象の次数を「対数体積」で評価する「系 3.12」で使用
される「多輻的アルゴリズム」の存在を主張する。
なお、[KF01]に出てくる少数の数式で使われる文字 q と Θ は、これらの対象を指す。
英語での用語中の pilot は、水先案内の意味で、日本語での用語中の「標」は目印の意味。

[HY01] p.44 は、これらの対象の主定理 3.11 や系 3.12 での役割を略述、[HY02]p.87 で、
より本格的な説明の準備のために説明し直しているのだが、[HY01] での略述の時点で筆者を
含む素人にとっては見なれない数論幾何の用語「数論的直線束」が出てくる。^^; 調べると、
（考察対象の（１点抜き）楕円曲線の）代数幾何的な「直線束」とエルミート計量の対という
定義が↓（英語にした "arithmetic line bundle" については）見つかったが…
https://www.tsuyama-ct.ac.jp/matsuda/AlgeGeo/algebraic_geometry_2013.pdf p.20
q-標対象 (q pilot object) や Θ標対象 (Θ pilot object) との関係は、
この定義を見ても、分かりやすくなってくれない。^^; もともと主定理を述べる直前に
定義される用語…ということで、厳密な定義には多大な準備が必要な概念らしい。
どうも＊圏論的に定式化された遠アーベル幾何の諸定理＊が基礎になっているようだ。

なお「数論的直線束の q パラメータ」というフレーズ全体での定義を、筆者は見つけて
いない。「考察対象の（１点抜き）楕円曲線に対して、「テイト曲線 (Tate curve) 」を
対応させて、その（ q という文字を慣例的に使う）テイト曲線のパラメータのこと？」
と推測した（∵ p 進数で、複素数係数でのフーリエ展開時のパラメタ q=exp(2πir) に
相当するものを考察するのが「テイト曲線」の理論らしいので）。しかし、その推測から
先に進めたり、推測を裏付けたりする資料が見つからないので、この方向の調査は保留し、
以下では [FI02] p.10 の説明を参考にした。

[FI02] p.10 での、＊○標対象という用語を表に出さない＊イメージ的な概念説明を見た
限り、「数論的直線束」は「q を生成元とする加群」、q は「悪い素点」に対して決まる
パラメータと思っておけるようだ。Θ 標対象は、この路線のイメージだと、以下のように
なりそうだ。
「l を 5以上の素数として、q' を qの2l乗根とする。また、l' = l^* = (l-1)/2 と書く。
T= {1≤m≤l'|(q')^(m^2)} という集合の各元について（「テータ関数の特殊値」とする
事により）テータリンクの両端で値が共通の意味を持つようにしたもの」が、Θ 標対象。
q 標対象もテータリンクの両端で値が共通の意味を持つように定義されているのだろう。
なお、l が「5以上の素数」とされるのは、l元体 F_l の乗法群（0 以外の要素全て: (F_l)-{0} ）の
T への作用が、「テータリンクの両端で値に共通の意味を持たせる（多輻的アルゴリズムを
構成する）」際に重要な役割を持つため。なお、上で「F_l の乗法群の作用」と書いているが、
厳密には／最終的には、符号の違いは無視した（{±1} による「商群」の）作用が使われる。
（∵[HY01]p.70 の「“LabCusp_K の対称性” に登場する重要な群」の説明と対応する話）。

なお、IUT 理論の文献は、「HTML での特殊文字の範囲」では書きにくい記号が多いし、
このブログのサーバーは LaTeX での記法をサポートしていないようなので、参照した文献
とは違う文字や記法を使った。そのための分かりにくさ（および、筆者の参照文献の誤読に
よる誤りなど）については、御容赦のほどを。