
微惑星と言っても現在の小惑星より大きく成長して直径500㎞を超えて集まったら、放射性同位体の崩壊熱で溶けて、コア、マントル、地殻に分化して原始惑星に成った後、岩石惑星に成長する原始惑星もあれば衝突で隕石クラスに分解される原始惑星もある。
と隕石の研究から分かって来た?26アルミニウムや60鉄などの半減期の短い放射性同位体はどこから供給されるのかは不明。業界では常識なので論文にいちいち書いてない可能性大。gyoukaideha以下、機械翻訳。
微惑星の磁場履歴の解明:熱進化とダイナモ生成のための洗練された多用途モデル
抽象的な
微惑星の熱と磁気の履歴は、地球の構成要素の形成と進化に関する独自の洞察を提供します。これらの履歴は、測定された特性を微惑星の挙動に変換する数値モデルを使用して、隕石から収集できます。この論文では、新しい1D微惑星の熱進化とダイナモ生成モデルを紹介します。この磁場生成モデルは、マントル対流と非共晶核の凝固の両方を含む、分化したマントル微惑星の最初のモデルです。より詳細な粘性モデルと、内部加熱と一致する停滞した蓋対流のパラメータ化を含めることで、マントル熱輸送の基本的な側面を改善しました。また、放射性加熱も追加しました。
60鉄金属の Fe-FeS コアで。さらに、熱と組成の浮力フラックスの組み合わせと最新の磁場スケーリング法則を実装して、コアの凝固が完了するまでの微惑星の熱進化中の磁場強度を予測します。半径 500 km の微惑星の例を実行して、モデル変更の結果を示します。これらの影響には、以前の研究と比較して、コアの熱成層の侵食がより速くなり、マントル対流の期間が長くなることが含まれます。コアの凝固による追加の浮力はダイナモの強度にわずかな影響しか与えませんが、初期のコアの硫黄含有量によっては、マントル対流が終了したときにダイナモが停止するのを防ぐことができます。私たちのモデルは、個々のパラメーターがダイナモ生成に与える影響を調査し、特定の隕石の親天体の特性を制限するために使用できます。これらの更新を組み合わせると、このモデルはこれまでで最も信頼性が高く完全な微惑星の磁場履歴を予測できるため、隕石の特性から微惑星の挙動を解読するための貴重なツールになります。
キーワード: 微惑星 磁場 熱履歴 隕石 内部
{ハイライト}
私たちのモデルは、微惑星の完全な磁場生成履歴を予測できます。
内向きの非共晶コア凝固によるダイナモ生成をモデル化できます。
微惑星マントルの対流と粘性に関する記述を改良しました。
1導入
岩石天体における磁場生成は、分化の程度や核とマントルの対流の活発さなど、天体内部の状態に依存します。微惑星は小さな岩石天体で、太陽系形成後数百万年(Ma)に集積し、地球型惑星の構成要素を形成しました。微惑星の中には現在も小惑星として存在し、隕石は地球に到達した微惑星の破片です。隕石に記録された磁化は、微惑星の進化や原始惑星系円盤のプロセスに関する重要な洞察を提供します。微惑星の熱進化と磁場生成モデルは、これらの天体と、これらの磁場を生成した太陽系星雲のプロセスの観点からこれらの残留磁化を解釈する上で非常に重要です。
ダイナモ作用によって磁場を発生させるためには、岩石体は部分的に溶融した金属核をもち、それが活発に運動している必要がある。核の流れは、熱対流または組成対流、あるいはその両方の組み合わせ、あるいは機械的な力によって駆動される。しかし、後者は微惑星には関係ないと考えられている(Dodds et al.,2021熱対流は温度による密度差によって駆動され、コア・マントル境界(CMB)を横切る熱流束が超断熱であることを必要とする。組成対流は、コアの凝固によって生じる化学的に誘導された密度差によって駆動される。例えば、現在、地球の磁場は、浮力のある非相溶性の軽い元素が凝固中の内核から液体の外核に分割され、それが上昇して液体の外核の対流を駆動することによって駆動されている(Braginsky、1963; ガビンズ、1977; ニモ、2007)。微惑星の内部磁場の過去の記録から、この天体は熱磁場の要件を満たしていたことがわかる(例えば、Wang et al.、2017)および/または構成的(例えば、Maurel et al.、2021)ダイナモ発電の歴史のある時点で。
太陽系の内側と外側から来たコンドライト隕石とアコンドライト隕石の古地磁気残留磁化は測定されている(例えばCarporzen et al.、2011; クルネデら、2015; 王ら、2017; ワイスら、2017これらの測定のいくつかは、バルク岩石に関連しています(例えば、Carporzen et al.、2011)、一方、コンドリュール中のダストオリビンなどの個々の相を測定するもの(例:Tarduno et al.、2012; フーら、2014)または金属を多く含む隕石中の雲状領域(例えば、ニコルスら、2021; モーレルら、2021)これらの測定と数値モデルを組み合わせることで、差別化された(例えばFu et al.、2012)および部分的に分化した小体(例えば、Elkins-Tanton et al.、2011; ブライソンら、2019b)によって生成された磁場。古地磁気残留磁化の年代が特定できれば、数値モデルを使用して、特定された時期に磁場を生成する母天体のサイズと特性の範囲を予測できます(例:Bryson et al.、2019b残留磁化の年代を特定できない場合は、数値モデルを使用して磁化が獲得された年代を推定することができます(例:Tarduno et al.、2012; ブライソンら、2015; ニコルズら、2021)。
いくつかの隕石は、CAI形成後4~5 Maまで原始惑星系円盤全体を貫いていた星雲場からの磁化を記録していると解釈されている(Wang et al.、2017)星雲領域は原始惑星系円盤からの恒星集積に影響を与えた(Wardle、2007; ワイスら、2021)であり、ディスク構造に影響を与えた可能性がある(Hu et al.、2019星雲領域の古地磁気記録は、ディスクの寿命を理解するのに役立ちます(Wang et al.、2017; ボルリナら、2022)、ディスク磁場の構造と強度(Cournede et al.,2015; ボルリナら、2021; ブライソンら、2023)、ディスク内の固体の動き(Bryson et al.,2020a、b)、および恒星の集積率(Weiss et al.,2021)個々のコンドリュール間の古地磁気方向はランダムに配向している(Fu et al.,2014、2020; ボルリナら、2021)は、これらのコンドリュール残留磁化が集積前であり、したがって微惑星集積前に星雲場の記録を獲得したに違いないという証拠を提供することができる。対照的に、古代のバルク古地磁気残留磁化は、これらの残留磁化がダイナモによって与えられたのか、それとも星雲場によって与えられたのかを判断するのに役立つ微惑星ダイナモ生成モデルを必要とする(例えば、Cournede et al.、2015; モーレルとガッタチェッカ、2024)。
微惑星におけるダイナモ生成については、これまでにもいくつかのモデルが提案されている(エルキンス・タントンら、2011; ステレンボルグとクロウリー、2012; ブライソンら、2019a; ドッズら、2021)。各モデルの反復には、パラメータ化されたマントル対流(SterenborgとCrowley、2012)、多段階集積(Bryson et al.,2019a)、漸進的な集積(Dodds et al.,2021)、またはコアの温度成層(Dodds et al.、2021これらのモデルは、ダイナモを生成できる微惑星のサイズの範囲を予測している(例えば、
>340 km ブライソンら、2019a)とダイナモの時期と期間(CAI形成後4~30 Ma、サイズに応じて5~25 Ma、Dodds et al.、2021さらに、これらのモデルは、CVコンドライト、Hコンドライト、アングリットなどの隕石母天体の特性を制限するためにも使用されてきた(Bryson et al .、2019a; ドッズら、2021)。コアの凝固と組成対流によるダイナモ生成に純粋に焦点を当てた他の数値モデルも開発されている。これらのモデルは、コアにおけるエントロピー散逸を固定するか(Nimmo、2009)またはIVA鉄隕石に焦点を当てるとマントルは存在しない(Scheinberg et al.、2016; ニューフェルドら、2019ここでは、微惑星の熱進化とダイナモ生成の改良モデルを紹介します。このモデルは、微惑星のダイナモ生成の制御を理解し、隕石の母天体の特性を復元するために使用できます。
これまでの各モデルでは新しい挙動が追加されてきましたが、マントルの熱輸送のいくつかの基本的な側面はモデル間で変更されておらず、ここで再検討されています。磁場生成には、コアの急速な冷却(超放射CMB熱流束)またはコアの固化が必要であり、そのためには熱をコアからマントルに移動させる必要があります。したがって、磁場生成のタイミングはマントルの冷却と本質的に関連しています。以前のモデルとは異なり、私たちが選択したマントル対流のスケーリング則は、内部加熱と表面および基底熱流束を持つ物体に適しており、2D数値シミュレーション(Deschamps and Vilella、2021; Thiriet et al.,2019)。マントル対流は粘性に大きく依存するため、以前のモデルから粘性法則を改良しました。私たちが選択したマントル対流のスケーリング則は、粘性パラメータの変化にも一貫して反応するため、ダイナモ生成に対する粘性の影響を十分に調査できます。さらに、マントル対流の停止の基準により、マントルが完全に伝導性になったときのCMB熱流束とマントル温度プロファイルの滑らかで物理的に現実的な動作が保証されます。コアでは、放射性核種による加熱も考慮しました。
60鉄
これにより、初期段階では核温度とマントルへの熱流束が上昇する可能性があります。
マントル対流と可変粘性に加えて、非共晶核凝固も考慮します。微惑星核凝固からのダイナモ生成のモデル化は困難です。なぜなら、安定または不安定な鉄デンドライトの成長、鉄の雪(Scheinberg et al.、2016);あるいはCMBからの固体鉄の粘性剥離(Neufeld et al.,2019凝固機構の不確実性のため、いくつかのモデルではマントル対流の終焉までの初期熱ダイナモのみを研究した(Sterenborg and Crowley、2012; ドッズら、2021)または、共晶凝固が組成ダイナモを駆動できないにもかかわらず、共晶凝固に要する時間を組成ダイナモがいつ生成されるかの代理として使用した(Bryson et al.、2019a)また、Bryson et al. (2019a)は、熱ダイナモと組成ダイナモで異なる磁場スケーリング則を使用しており、コアの流れを同時に駆動する両方のメカニズムを考慮に入れることができませんでした。非共晶コア凝固を考慮したモデルは、マントルされていない微惑星に焦点を当てています(Scheinberg et al.、2016; ニューフェルドら、2019)あるいは天体の初期の熱史におけるマントル対流を無視している(ニコルズら、2021ここでは、非共晶コア凝固による磁場生成のモデルを開発しました。このモデルでは、コア凝固中の磁場生成に対する熱浮力と組成浮力の相対的な寄与も考慮されています。
本論文では、第2章で改良された 1D 球対称熱進化モデルについて説明します。第3章では、実行例の結果を示し、モデル変更の影響について説明します。第 4章、第 5 章、第 6 章では、それぞれ集積と分化、マントルの溶融、コアの凝固に関する仮定の正当性を説明します。第7章では、モデルの将来的な応用とさらなる改良の余地について説明し、第8章で結論を述べます。
2熱進化モデル
2.1概要
微惑星の熱進化の重要な段階を図1に示す。集積後、微惑星は放射性崩壊により加熱される。
26Al (𝑡1/2=0.717Ma、ノイマン他、2012)十分に早い時期に集積が起こった場合(1.5~2.5 Ma以内、Neumann et al.、2012; モネローら、2023)では、微惑星は十分に高い温度に達して融解し、分化して核とマントルを形成します。
分化の過程で26Alマントルに分配され、放射性60鉄 (𝑡1/2=2.62Ma、ルエダス、2017)がコアに分配される。これら 2 つの同位体はそれぞれマントルとコアを加熱し、マントルは対流に対して不安定になる。微惑星はサイズが小さいため断熱勾配が小さいため、コア対流の基準や CMB 全体の熱流の方向を決定する際にコア断熱を無視する。マントルがコアよりも高温になると(たとえば、内部加熱が強く、表面熱流束が低いため)、コアは上からマントルによって加熱され、浅い深さで熱成層化される(Dodds ら、2021マントルがコアよりも冷たくなると、コアも冷え始める。CMBの熱流束は、FCMBSが正であれば、コア対流が始まります。磁気レイノルズ数、𝑅𝑒mが臨界値を超えると、この対流はダイナモの開始につながる可能性がある。マントルが冷えると粘性が高くなり、マントル対流は停止し、マントル内の熱は伝導によって輸送される。最初は、マントル対流の停止は減少する。
FCMBS亜臨界状態につながる可能性がある 𝑅𝑒mそしてダイナモの停止。その後、マントル伝導の過程で、
FCMBS十分に増加すると、𝑅𝑒m再び超臨界状態になり、ダイナモが再起動します。コアが液相線以下に冷却されると、コアの凝固が始まります。これにより、軽元素(炭素、硫黄など)が放出されるため、コアダイナモの浮力源が追加され、ダイナモ発電の2回目の周期(または1回目/2回目の周期の延長)が発生する可能性があります。コアが完全に凝固すると、ダイナモ発電はできなくなります。
次のセクションでは、1D 球対称モデルについて詳しく説明します。まずマントル粘性モデルから始め、次に熱進化の各段階を説明し、最後に磁場生成と数値実装について説明します。モデルの仮定については、セクション4、5、6で説明します。

図1:微惑星の熱進化の段階を示す図。青(核)と紫(マントル)のラベルは、ステレンボルグとクロウリーのモデルと比較して、私たちのモデルで採用された重要な改良点を強調しています(2012); ブライソンら(2019a)およびDodds et al. (2021これまでのモデルでは、マントル対流の終了後、コアの凝固(ステージ 7)による磁場生成のみを考慮していました。しかし、私たちのモデルでは、コアの凝固前に磁場が 2 回発生する可能性を考慮しています。磁気レイノルズ数が臨界値を超えると、ステージ 4、6、7 で磁場生成が発生する可能性があります。初期のコアの硫黄含有量が低い場合、マントル対流が停止する前にコアが凝固し始め、ダイナモ生成が一時停止しない可能性があります(ステージ 5)。
2.2マントル粘性
マントル粘性は、マントル温度と溶融率の変動により、微惑星の熱進化中に何桁も変化し、マントルの冷却に大きな影響を与えます。マントル粘性は、対流中およびマントル対流から伝導への移行中のマントル境界層の厚さを制御し、CMB 熱流束とダイナモ生成に影響します。このモデルでは、温度によるレオロジー挙動の変化を捉えるために 4 つの粘性則を定義し、粘性則と対流パラメータ化が自己整合的であり、粘性パラメータの不確実性を反映するように完全に調整できることを保証します。
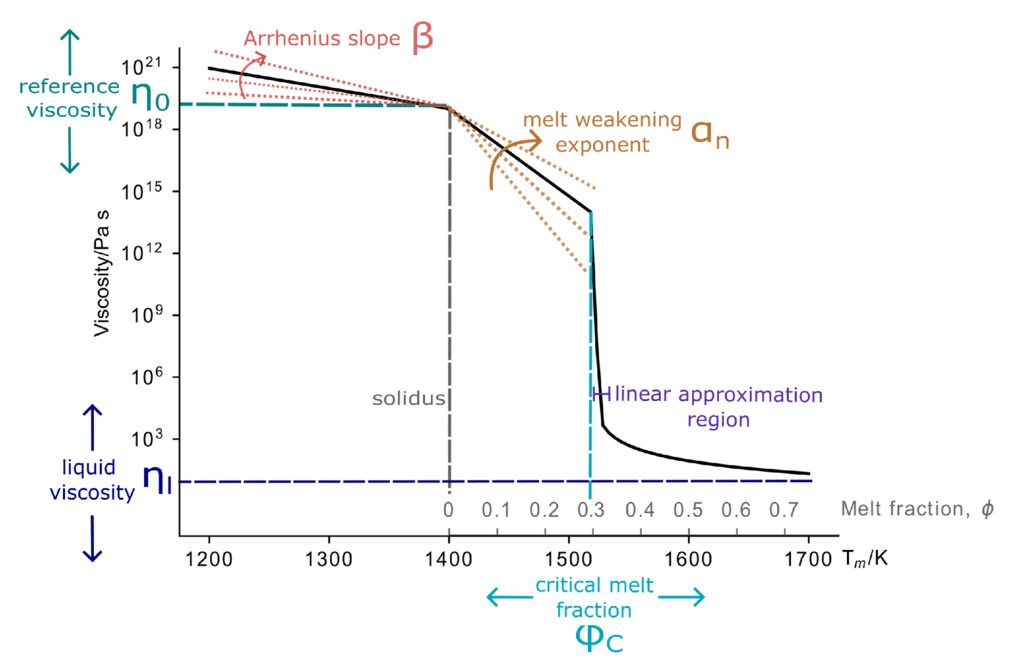
図2 :マントル粘性の温度変化(黒実線)
𝜂0 =10^19Pas、𝜙c =0.3、𝛽 = 0.0225K^−1 𝛼n =30、 そして𝜂𝑙 = 10 Pas。各パラメータの変化による影響は、色付きの矢印と線で示されています。水平軸の灰色の上部の目盛りは、マントルの固相線温度がそれぞれ 1400 K、液相線温度が 1800 K の場合の固相線以上の温度での等価溶融分率を示しています。
マントル粘性の温度依存性は、5つの制御変数(図2 )によって区分的に定義される:臨界溶融率、
𝜙c、アレニウスの傾き、𝛽、溶融弱化指数、𝛼n、固相線における基準粘度、𝜂0、液体の粘度、𝜂𝑙:

ここ𝑇m、sそして𝑇m、l
それぞれマントルの固相線温度と液相線温度である。𝑇𝜙𝑐は気温はΦcそして𝜂c=𝜂(𝑇𝜙𝑐)粘度は𝜙c
は式1bで計算されます。溶融率、
𝜙
線形液相線近似を仮定して計算されます。
𝜙=𝑇−𝑇m,s/𝑇m,l−𝑇m,sマントルの組成は指定せず、同じ珪酸塩固相線を仮定する。
𝑇m,s=1400 K、液相線、𝑇m,l=1800 K、Bryson et al. の値(2019a)およびDodds et al. (2021)(第5.1節参照)。マントルの固相線と液相線は圧力に依存しない定数である。これは微惑星マントルの圧力変化が小さいためである(<50MPa)。
固相線以下では、粘度はアレニウス温度依存性を持つ(式1a)。この依存性は、基準温度におけるフランク・カメネツキー近似を使用してモデル化される。
𝑇ref、および基準粘度、𝜂0、E/𝑅𝑇≈E(𝑇−𝑇ref)/𝑅g𝑇ref^2 = 𝛽(𝑇−𝑇m,s)、 どこ
Eは活性化エネルギーは
𝑅g = 8.31JK^−1mol^−1
は気体定数であり、マントル固相線が基準温度とされる(Frank-Kamenetskii、1969)固相線より上で、臨界融解率より下では、この運動学的アレニウス依存性は、さらに融解弱化依存性を持つ。
αn𝜙=𝛼n𝑇−𝑇m,s/𝑇m,l−𝑇m,s (式1b)。粘度は急激に低下し、
𝜙c溶融物が残りの固体相を囲み、物質が分解するためである。
𝜙c粘性はクリーガー・ドハティ関係式(ファロウギとフーバー、2015; スターツら、2022)(式1d)は、溶融分率が1に近づくにつれて液体粘度が一定になる傾向がある。
式1cは、dlog10𝜂/d𝑇 = Δ𝜂/w 粘度の急激な低下における数値安定性を確保するため
𝜙c。wは、この近似によってカバーされる領域の幅であり、近似領域を最小限に抑えながら数値安定性を確保するために 5 K に設定されています。
Δ𝜂 = log10(𝜂(𝑇𝜙𝑐+w))−log10(𝜂(𝑇𝜙𝑐))粘度の対数差は𝜙c、式1bで決定され、粘度は𝑇𝜙𝑐+w 式1dによって決定される。
アレニウス温度依存性(式1a)は粘性温度スケールを決定する。
Δ𝑇/∱rh 対流を制御する対流領域全体の温度差の割合を決定する(ミショーとノイフェルド、2022; ダヴァイユとジョパール、1993)

この定義では、𝑇m 対流領域(マントル)の温度であり、
Δ𝑇 内部と境界面(マントルの場合)の温度差である。
Δ𝑇=𝑇m−𝑇𝑠)。
Brysonらの3ピースモデルと比較すると、2019a)このモデルは数値安定性を近似した領域が1桁狭いため、
w、そしてクリーガー・ドハティの関係を粘度に適用する。
𝜙c定数値を想定するのではなく、タンDodds らが採用した近似値(2021)は、固相線での傾きの変化を捉え、粘性率の勾配が急である。
𝜙c
物理的に意味のあるパラメータを使用して調整できます。
2.3蓄積
私たちのモデルは、特定の時間に200 Kでケイ酸塩とFe-FeSの未分化混合物が瞬間的に集積することから始まる。
tacc、CAI形成後。微惑星表面の熱流束の範囲は十分に小さいため、平衡表面温度への影響は無視できるため、シミュレーション全体を通じて微惑星表面温度は平衡温度200 Kに固定されています(<10 K; ドッズら、2021)植物胚中心では、∂𝑇/∂𝑟𝑟=0 = 0シミュレーション全体を通して。
2.4差別化前
集積後、微惑星は26Alそして60鉄の放射性崩壊により熱くなり、熱はまず伝導によって体内を運ばれる。

どこ𝜌密度はC𝑝比熱容量は𝑇温度は𝑟半径は𝑡時間であり、kは熱伝導率です。下付き文字chは未分化コンドライト物質の値を表します。未分化微惑星はケイ酸塩マントルと同じ熱特性を持つと仮定されます(例:Elkins-Tanton et al.、2011; ブライソンら、2019a)は、密度を除いて、微惑星の嵩密度を使用する。微惑星の分化前の圧縮と焼結は無視され、一貫して一定の熱拡散率が使用される。なぜなら、これらのプロセスは、微惑星が最初に200 Kから700 Kに加熱されるときにのみ微惑星に影響を与えるからである(Yomogida and Matsui、1984)であり、全体的な熱の進化に最小限の影響しか与えません。
𝐻単位質量あたりの放射加熱力である

どこ𝐻i、0同位体の単位質量あたりの加熱力である
ICAI設立当時、fi最も一般的な安定同位体に対する放射性同位体の豊富さの比率である。
Xiは、集積物質中の元素存在比(重量%)であり、𝑡1/2,iは放射性同位体の半減期である。各パラメータに選択された値は表1にまとめられている。微惑星が加熱されるにつれて金属とケイ酸塩が融解することは、修正された比熱容量(Merk et al.,2002; ドッズら、2021(金属とケイ酸塩の混合物)
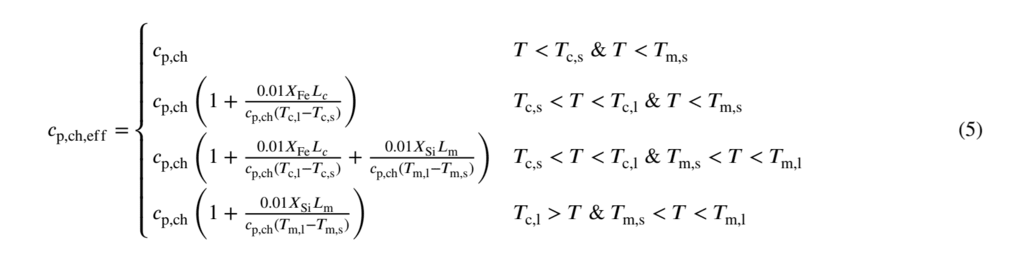
ここX鉄そしてXsiは、付着物質中のFe-FeSおよびケイ酸塩の割合(重量%)である。
LcそしてLm Fe-FeSとケイ酸塩の融解潜熱である。
𝑇c、lそして𝑇m、l Fe-FeSとケイ酸塩の液体であり、𝑇c、sそして𝑇m、s
Fe-FeSとケイ酸塩の固相線である。Fe-FeSとケイ酸塩の溶融分率は、両方とも線形液相線近似を使用して計算される。Fe-FeS系の硫黄含有量は、入力パラメータとして設定される。共晶Fe-FeS組成の微惑星の場合、微惑星の温度がFe-FeS固相線に達すると、すべてのFe-FeSが溶融するまで温度は固定される。このシナリオでは、Fe-FeS溶融分率の時間変化は、
𝜙鉄は、式3の左側の項を次のように置き換えることによって計算されます。
𝜌chX鉄L鉄∂𝜙鉄/∂𝑡どこ𝜌chX鉄
未分化物質中の Fe-FeS の密度です。
固体の停滞蓋対流(セクション2.5.2)は、分化の前に、天体が加熱されるにつれて始まる可能性がある。この対流モードでは、停滞蓋は、厚さ10nmの微惑星の表面にある導電性の不動境界層である。
𝛿0(式7)そして蓋の下の内部は対流する(図3)。微惑星内の圧力変化は断熱温度勾配を無視できるほど小さいため、内部は等温であると仮定される。内部温度は、𝑇iに従って進化する

どこFlid = −Kchd𝑇/d𝑟|𝑟=𝑅−𝛿0、Vi内部の容積であり、Alid停滞した蓋の底の表面積である(ソロマトフ、1995)。 停滞した蓋は、内部と蓋の放射性元素の量が等しいと仮定すると、式3に従って熱を輸送し続け、微惑星が加熱されるにつれて厚さが減少する。 微惑星が対流している間に共晶Fe-FeSの溶融が起こる場合、式6の左辺は次のように置き換えられる。
𝜌chX鉄L鉄∂𝜙鉄/∂𝑡固体の停滞したlidの対流は、𝛿0微惑星の半径の99%未満である。𝑅。
ケイ酸塩溶融分画が𝜙臨界溶融率に達すると、𝜙c、ケイ酸塩の粘度が急激に低下し、レインアウトによって分化が進行します。レインアウトでは、より密度の高い溶融Fe-FeSが、ストークス沈降によって密度の低い低粘度のケイ酸塩に沈降します。このプロセスは迅速です(10^4ミリメートルサイズの液滴の場合(S5を参照)であり、瞬間的に近似することができる。
𝜙=𝜙cこの過程の時間スケールの不確実性のため、この温度は無視される(セクション4およびセクションS5を参照)。内部圧力勾配が小さいため、物体はほぼ等温であり、単純化のため、微惑星全体が同時に分化すると仮定する。我々のモデルでは、分化前にすべてのFe-FeSが完全に溶融し、核は最初は液体であると仮定する。この仮定を満たすためには、Fe-FeSの初期核硫黄含有量の液相線温度は、
𝜙cこれにより、初期のコア硫黄含有量の範囲が制限されます(セクション4.3.1を参照)。
分化の時点で、物体は瞬時にFe-FeS核を形成し、その半径は物体の半分であると想定される。
𝑟𝑐=𝑅/2、その上にケイ酸塩マントルが重なる(図3)。核とマントルは臨界溶融率の温度で等温であり、
𝑇𝜙c鉄はすべて核に分配され、アルミニウムはすべてマントルに留まると仮定する。これにより、
26Alマントルと60鉄初期状態と比較したコアの硫黄含有量。初期コアの硫黄含有量は、XS、0
は入力パラメータによって設定され、未分化微惑星中の Fe-FeS の硫黄含有量と同じです。
2.5分化後
2.5.1クラスト
地殻の存在は、固定表面温度境界条件に簡略化されています。表面ノードのみが、微分化できるほど高温になりません。したがって、多孔質レゴリスの厚さはこのモデルの解像度を下回るため、無視されています(セクション4.2)。
2.5.2マントル
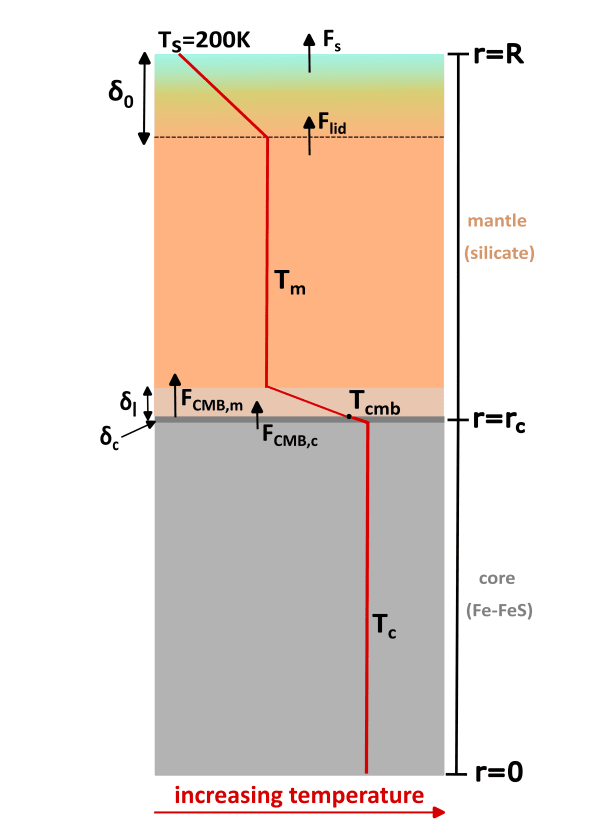
図3 :対流するケイ酸塩マントルと対流するFe-FeSコアのモデル設定を示す概略図。コアとマントルは結合した2つの貯留層です。地殻は固定された表面温度で近似されます。
𝑇𝑠 = 200 K. 赤い線は微惑星の温度プロファイルで、温度は右に行くほど高くなります。この図では、マントルは停滞した蓋の領域で対流しています。内部は等温で、CMBには伝導境界層があります。
𝛿𝑙、そして表面、𝛿0黒い破線は停滞したlidの底部を示しています。核にはCMBに熱境界層があり、
𝛿𝑐マントルとコアが伝導性である場合、代わりに各層全体に温度勾配が存在する。CMB熱流束のバランス(FCMBS、m = FCMBS、c)はCMB温度を計算するために使用される𝑇CMBS
記号の意味はセクション2.5.2と2.5.3に記載されています。
マントルは伝導または停滞蓋対流によって熱を輸送する。停滞蓋対流では、マントルは等温の対流内部を持ち、表面の下に伝導境界層(「停滞蓋」)があり、CMBの上にもう1つあると想定される(図3)。我々が採用したパラメータ化では、停滞蓋の厚さには蓋の底部の薄い可動境界層が含まれる(セクションS1.2.2を参照)。停滞蓋の厚さについては経験的に決定された式を仮定する。
𝛿0、内部加熱、上部境界と下部境界での熱流束、温度依存粘性、および自由滑り境界条件(DeschampsとVilella、2021)


図4 :コア上部の不安定層の対流混合によるコア熱成層の侵食の概略図。赤い線は温度プロファイルを示し、温度は右に向かって上昇します。赤い破線は対流に対して不安定なコアの部分を示します。図の上部は、マントル内のCMB境界層の上にある対流マントルの基部です。
𝛿𝑙、そして核内のCMB境界層、𝛿c
時間は左から右へ進む(a–c)。破線はマントルとコアのCMB境界層を示す。コアのCMB境界層(下の破線)は、コアが対流しているときにのみ存在する。コアの熱成層は、マントルの冷却(マントルの温度プロファイルをコアのそれに対して左にシフトさせる)または加熱によって侵食される。
60鉄コア内(マントルに対してコアの温度プロファイルを右にシフトさせる)。すべての記号はセクション2.5.3で定義されています。
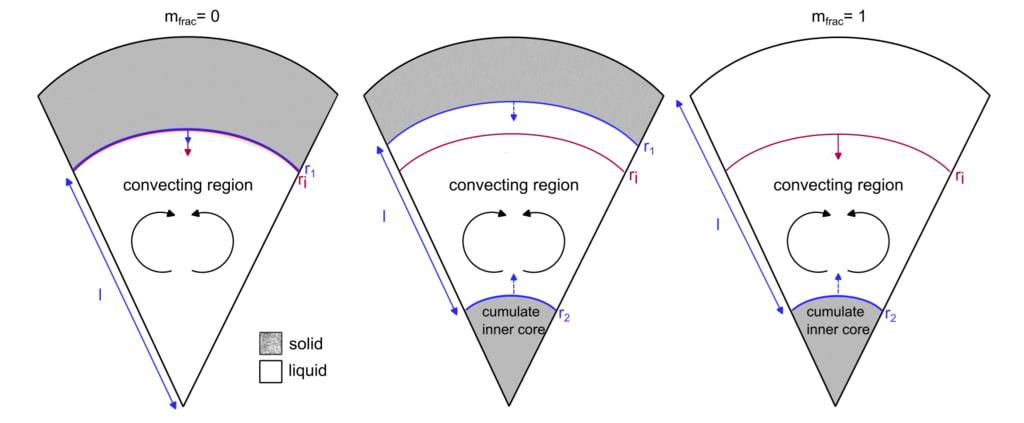
図5 :コア凝固の形状を示す概略図。凝固材料の量は次のようにパラメータ化されます。
𝑟i(マゼンタの線)対流の長さスケールは次のように表される。
𝑙=𝑟1−𝑟2
微惑星核の固化のメカニズムの不確実性を考慮するために、2つの端成分形状を考察する(図の中央のシナリオは中間の形状も示している)。1つの端成分では、mfrac = 0では、コアの安定した固体部分はCMBから内側に向かって成長します。もう一方の端成分では、mfrac =1の場合、固まった鉄はすべて再溶融せずに落下し、集積した内核を形成します。
mfrac = 0では、対流の長さスケールはコアが固まるにつれて最もゆっくりと減少し、mfrac =1 の場合、対流の長さスケールは最も速く減少します。微惑星コアの固化のメカニズムが不確実であるため、各シナリオで対流がどのように駆動されるかを規定せず、長さスケールの変化のみに焦点を当てます。両方のエンドメンバーで、固化領域の固体分率は 100% であると仮定します。詳細と議論については、セクション2.5.4と6.1を参照してください。
7見通し
私たちのモデルには、以前のモデルでは無視されたり単純化されたりしていたいくつかの物理的および化学的特徴が含まれています。たとえば、私たちの微惑星熱進化モデルは、マントル対流も含むマントル微惑星の非共晶核凝固をモデル化した初めてのモデルです。統一された浮力フラックスを計算することで、同じスケーリング則を使用することができます。
𝑅𝑒m熱の進化を通して磁場の強さと熱対流の同時発生を可能にする。さらに、
60鉄コアの熱構造に、対流の段階的な停止と境界層の厚さをモデル化するために、マントル対流のパラメータ化を調整することも選択しました。これは、表面冷却と内部加熱を伴うシステムに適用できます。マントル粘性関数に物理的に現実的な値を実装し、粘性関数に追加の部分を追加して、温度の関数として粘性挙動の全範囲を捉えるようにしました。マントル粘性の変化に反応するように、停滞蓋スケーリング則も実装しました。これにより、将来の研究では、特定のサイズと組成の微惑星に最も適した粘性パラメータを選択できるようになります。モデルの他のパラメータは完全に調整可能であり、特定のパラメータの影響に関する将来の研究や、隕石の古地磁気記録の解釈を可能にするために特定の隕石母天体に適用することができます。別の研究では、マントル粘性、原始的粘性、および原始的粘性係数を体系的に変化させます。
60鉄/56鉄、初期の核硫黄含有量、微惑星のサイズなど、これらのパラメータがダイナモ生成に与える影響についてより深く理解し、隕石の古地磁気記録に対する私たちのモデルの意味を理解するために、研究が進められている(Sanderson et al.、2024)。
部分的な分化と地殻形成を組み込むことで、モデルに若干の改善を加えることができます。また、2 つの重要な改良点があります。まず、微惑星の分化のメカニズムと初期の核の硫黄含有量を調和させる必要があります。微惑星の核が最初は硫黄含有量の低い状態で形成されるか、または後に硫黄を失うか、そしてこれらの要因が核の固化とダイナモ生成の開始にどのような影響を与えるかについては、さらに研究する必要があります。次に、マントルに包まれた微惑星の核の内側への固化の考えられるメカニズムと、これがダイナモ生成に与える影響について、さらに詳しく調査する必要があります。
8結論
微惑星は太陽系形成後の最初の数百万年間に形成され、その多くが地球型惑星に集積しました。熱進化およびダイナモ生成モデルは、これらの微惑星の内部構造と熱履歴に関する洞察を提供します。ただし、以前のモデルはダイナモ生成の初期または後期のいずれかに焦点を当てていたため、完全な磁場履歴を予測する能力が制限されていました。私たちのモデルは、マントル対流の記述と非共晶コアの凝固のパラメータ化に焦点を当て、微惑星の熱進化とダイナモ生成に関する統一された、より汎用性の高いモデルを提供します。具体的な機能強化は次のとおりです。
• 放射性加熱による60鉄コアの中に。
• マントル対流のパラメータ化と自己整合し、マントル粘性の影響を調査するために調整できるマントル粘性モデル。
• 境界熱流束と内部加熱と一致する停滞蓋と CMB 境界層のパラメータ化。
• 停滞蓋とCMB境界層の厚さの合計がマントルの厚さよりも大きい場合の対流の停止。
• 磁場生成を促進するための統一された熱および組成浮力フラックスを備えた非共晶コア凝固のパラメータ化モデル。
• ダイナモ生成の期間における磁場強度の計算。
私たちのモデルに実装されたこれらの変更の主な結果は、半径 500 km の微惑星に対して生成された磁気履歴の例によって実証されています。以前のモデルと比較すると、次のことがわかります。
• 核熱成層はより急速に侵食されます。
• マントル対流とダイナモ発生の最初の時代がより長く続きます。
• コアの固化により双極子場の強度はわずかに増加しますが、マントル対流の停止後に追加の浮力源を提供することで、ダイナモの持続時間に対するより強力な制御が行われます。
• ダイナモ生成の第二期は、コアの固化によって引き起こされるものではありません。
私たちのモデルは、組成ダイナモと熱ダイナモの両方の磁場強度を持つ微惑星の完全な磁場生成履歴を予測できます。したがって、このモデルは、微惑星のダイナモ生成の一般的な制御を理解し、隕石の母天体の古地磁気記録からその特性に関する制約を回復するための強力なツールとして機能する可能性があります。
と隕石の研究から分かって来た?26アルミニウムや60鉄などの半減期の短い放射性同位体はどこから供給されるのかは不明。業界では常識なので論文にいちいち書いてない可能性大。gyoukaideha以下、機械翻訳。
微惑星の磁場履歴の解明:熱進化とダイナモ生成のための洗練された多用途モデル
抽象的な
微惑星の熱と磁気の履歴は、地球の構成要素の形成と進化に関する独自の洞察を提供します。これらの履歴は、測定された特性を微惑星の挙動に変換する数値モデルを使用して、隕石から収集できます。この論文では、新しい1D微惑星の熱進化とダイナモ生成モデルを紹介します。この磁場生成モデルは、マントル対流と非共晶核の凝固の両方を含む、分化したマントル微惑星の最初のモデルです。より詳細な粘性モデルと、内部加熱と一致する停滞した蓋対流のパラメータ化を含めることで、マントル熱輸送の基本的な側面を改善しました。また、放射性加熱も追加しました。
60鉄金属の Fe-FeS コアで。さらに、熱と組成の浮力フラックスの組み合わせと最新の磁場スケーリング法則を実装して、コアの凝固が完了するまでの微惑星の熱進化中の磁場強度を予測します。半径 500 km の微惑星の例を実行して、モデル変更の結果を示します。これらの影響には、以前の研究と比較して、コアの熱成層の侵食がより速くなり、マントル対流の期間が長くなることが含まれます。コアの凝固による追加の浮力はダイナモの強度にわずかな影響しか与えませんが、初期のコアの硫黄含有量によっては、マントル対流が終了したときにダイナモが停止するのを防ぐことができます。私たちのモデルは、個々のパラメーターがダイナモ生成に与える影響を調査し、特定の隕石の親天体の特性を制限するために使用できます。これらの更新を組み合わせると、このモデルはこれまでで最も信頼性が高く完全な微惑星の磁場履歴を予測できるため、隕石の特性から微惑星の挙動を解読するための貴重なツールになります。
キーワード: 微惑星 磁場 熱履歴 隕石 内部
{ハイライト}
私たちのモデルは、微惑星の完全な磁場生成履歴を予測できます。
内向きの非共晶コア凝固によるダイナモ生成をモデル化できます。
微惑星マントルの対流と粘性に関する記述を改良しました。
1導入
岩石天体における磁場生成は、分化の程度や核とマントルの対流の活発さなど、天体内部の状態に依存します。微惑星は小さな岩石天体で、太陽系形成後数百万年(Ma)に集積し、地球型惑星の構成要素を形成しました。微惑星の中には現在も小惑星として存在し、隕石は地球に到達した微惑星の破片です。隕石に記録された磁化は、微惑星の進化や原始惑星系円盤のプロセスに関する重要な洞察を提供します。微惑星の熱進化と磁場生成モデルは、これらの天体と、これらの磁場を生成した太陽系星雲のプロセスの観点からこれらの残留磁化を解釈する上で非常に重要です。
ダイナモ作用によって磁場を発生させるためには、岩石体は部分的に溶融した金属核をもち、それが活発に運動している必要がある。核の流れは、熱対流または組成対流、あるいはその両方の組み合わせ、あるいは機械的な力によって駆動される。しかし、後者は微惑星には関係ないと考えられている(Dodds et al.,2021熱対流は温度による密度差によって駆動され、コア・マントル境界(CMB)を横切る熱流束が超断熱であることを必要とする。組成対流は、コアの凝固によって生じる化学的に誘導された密度差によって駆動される。例えば、現在、地球の磁場は、浮力のある非相溶性の軽い元素が凝固中の内核から液体の外核に分割され、それが上昇して液体の外核の対流を駆動することによって駆動されている(Braginsky、1963; ガビンズ、1977; ニモ、2007)。微惑星の内部磁場の過去の記録から、この天体は熱磁場の要件を満たしていたことがわかる(例えば、Wang et al.、2017)および/または構成的(例えば、Maurel et al.、2021)ダイナモ発電の歴史のある時点で。
太陽系の内側と外側から来たコンドライト隕石とアコンドライト隕石の古地磁気残留磁化は測定されている(例えばCarporzen et al.、2011; クルネデら、2015; 王ら、2017; ワイスら、2017これらの測定のいくつかは、バルク岩石に関連しています(例えば、Carporzen et al.、2011)、一方、コンドリュール中のダストオリビンなどの個々の相を測定するもの(例:Tarduno et al.、2012; フーら、2014)または金属を多く含む隕石中の雲状領域(例えば、ニコルスら、2021; モーレルら、2021)これらの測定と数値モデルを組み合わせることで、差別化された(例えばFu et al.、2012)および部分的に分化した小体(例えば、Elkins-Tanton et al.、2011; ブライソンら、2019b)によって生成された磁場。古地磁気残留磁化の年代が特定できれば、数値モデルを使用して、特定された時期に磁場を生成する母天体のサイズと特性の範囲を予測できます(例:Bryson et al.、2019b残留磁化の年代を特定できない場合は、数値モデルを使用して磁化が獲得された年代を推定することができます(例:Tarduno et al.、2012; ブライソンら、2015; ニコルズら、2021)。
いくつかの隕石は、CAI形成後4~5 Maまで原始惑星系円盤全体を貫いていた星雲場からの磁化を記録していると解釈されている(Wang et al.、2017)星雲領域は原始惑星系円盤からの恒星集積に影響を与えた(Wardle、2007; ワイスら、2021)であり、ディスク構造に影響を与えた可能性がある(Hu et al.、2019星雲領域の古地磁気記録は、ディスクの寿命を理解するのに役立ちます(Wang et al.、2017; ボルリナら、2022)、ディスク磁場の構造と強度(Cournede et al.,2015; ボルリナら、2021; ブライソンら、2023)、ディスク内の固体の動き(Bryson et al.,2020a、b)、および恒星の集積率(Weiss et al.,2021)個々のコンドリュール間の古地磁気方向はランダムに配向している(Fu et al.,2014、2020; ボルリナら、2021)は、これらのコンドリュール残留磁化が集積前であり、したがって微惑星集積前に星雲場の記録を獲得したに違いないという証拠を提供することができる。対照的に、古代のバルク古地磁気残留磁化は、これらの残留磁化がダイナモによって与えられたのか、それとも星雲場によって与えられたのかを判断するのに役立つ微惑星ダイナモ生成モデルを必要とする(例えば、Cournede et al.、2015; モーレルとガッタチェッカ、2024)。
微惑星におけるダイナモ生成については、これまでにもいくつかのモデルが提案されている(エルキンス・タントンら、2011; ステレンボルグとクロウリー、2012; ブライソンら、2019a; ドッズら、2021)。各モデルの反復には、パラメータ化されたマントル対流(SterenborgとCrowley、2012)、多段階集積(Bryson et al.,2019a)、漸進的な集積(Dodds et al.,2021)、またはコアの温度成層(Dodds et al.、2021これらのモデルは、ダイナモを生成できる微惑星のサイズの範囲を予測している(例えば、
>340 km ブライソンら、2019a)とダイナモの時期と期間(CAI形成後4~30 Ma、サイズに応じて5~25 Ma、Dodds et al.、2021さらに、これらのモデルは、CVコンドライト、Hコンドライト、アングリットなどの隕石母天体の特性を制限するためにも使用されてきた(Bryson et al .、2019a; ドッズら、2021)。コアの凝固と組成対流によるダイナモ生成に純粋に焦点を当てた他の数値モデルも開発されている。これらのモデルは、コアにおけるエントロピー散逸を固定するか(Nimmo、2009)またはIVA鉄隕石に焦点を当てるとマントルは存在しない(Scheinberg et al.、2016; ニューフェルドら、2019ここでは、微惑星の熱進化とダイナモ生成の改良モデルを紹介します。このモデルは、微惑星のダイナモ生成の制御を理解し、隕石の母天体の特性を復元するために使用できます。
これまでの各モデルでは新しい挙動が追加されてきましたが、マントルの熱輸送のいくつかの基本的な側面はモデル間で変更されておらず、ここで再検討されています。磁場生成には、コアの急速な冷却(超放射CMB熱流束)またはコアの固化が必要であり、そのためには熱をコアからマントルに移動させる必要があります。したがって、磁場生成のタイミングはマントルの冷却と本質的に関連しています。以前のモデルとは異なり、私たちが選択したマントル対流のスケーリング則は、内部加熱と表面および基底熱流束を持つ物体に適しており、2D数値シミュレーション(Deschamps and Vilella、2021; Thiriet et al.,2019)。マントル対流は粘性に大きく依存するため、以前のモデルから粘性法則を改良しました。私たちが選択したマントル対流のスケーリング則は、粘性パラメータの変化にも一貫して反応するため、ダイナモ生成に対する粘性の影響を十分に調査できます。さらに、マントル対流の停止の基準により、マントルが完全に伝導性になったときのCMB熱流束とマントル温度プロファイルの滑らかで物理的に現実的な動作が保証されます。コアでは、放射性核種による加熱も考慮しました。
60鉄
これにより、初期段階では核温度とマントルへの熱流束が上昇する可能性があります。
マントル対流と可変粘性に加えて、非共晶核凝固も考慮します。微惑星核凝固からのダイナモ生成のモデル化は困難です。なぜなら、安定または不安定な鉄デンドライトの成長、鉄の雪(Scheinberg et al.、2016);あるいはCMBからの固体鉄の粘性剥離(Neufeld et al.,2019凝固機構の不確実性のため、いくつかのモデルではマントル対流の終焉までの初期熱ダイナモのみを研究した(Sterenborg and Crowley、2012; ドッズら、2021)または、共晶凝固が組成ダイナモを駆動できないにもかかわらず、共晶凝固に要する時間を組成ダイナモがいつ生成されるかの代理として使用した(Bryson et al.、2019a)また、Bryson et al. (2019a)は、熱ダイナモと組成ダイナモで異なる磁場スケーリング則を使用しており、コアの流れを同時に駆動する両方のメカニズムを考慮に入れることができませんでした。非共晶コア凝固を考慮したモデルは、マントルされていない微惑星に焦点を当てています(Scheinberg et al.、2016; ニューフェルドら、2019)あるいは天体の初期の熱史におけるマントル対流を無視している(ニコルズら、2021ここでは、非共晶コア凝固による磁場生成のモデルを開発しました。このモデルでは、コア凝固中の磁場生成に対する熱浮力と組成浮力の相対的な寄与も考慮されています。
本論文では、第2章で改良された 1D 球対称熱進化モデルについて説明します。第3章では、実行例の結果を示し、モデル変更の影響について説明します。第 4章、第 5 章、第 6 章では、それぞれ集積と分化、マントルの溶融、コアの凝固に関する仮定の正当性を説明します。第7章では、モデルの将来的な応用とさらなる改良の余地について説明し、第8章で結論を述べます。
2熱進化モデル
2.1概要
微惑星の熱進化の重要な段階を図1に示す。集積後、微惑星は放射性崩壊により加熱される。
26Al (𝑡1/2=0.717Ma、ノイマン他、2012)十分に早い時期に集積が起こった場合(1.5~2.5 Ma以内、Neumann et al.、2012; モネローら、2023)では、微惑星は十分に高い温度に達して融解し、分化して核とマントルを形成します。
分化の過程で26Alマントルに分配され、放射性60鉄 (𝑡1/2=2.62Ma、ルエダス、2017)がコアに分配される。これら 2 つの同位体はそれぞれマントルとコアを加熱し、マントルは対流に対して不安定になる。微惑星はサイズが小さいため断熱勾配が小さいため、コア対流の基準や CMB 全体の熱流の方向を決定する際にコア断熱を無視する。マントルがコアよりも高温になると(たとえば、内部加熱が強く、表面熱流束が低いため)、コアは上からマントルによって加熱され、浅い深さで熱成層化される(Dodds ら、2021マントルがコアよりも冷たくなると、コアも冷え始める。CMBの熱流束は、FCMBSが正であれば、コア対流が始まります。磁気レイノルズ数、𝑅𝑒mが臨界値を超えると、この対流はダイナモの開始につながる可能性がある。マントルが冷えると粘性が高くなり、マントル対流は停止し、マントル内の熱は伝導によって輸送される。最初は、マントル対流の停止は減少する。
FCMBS亜臨界状態につながる可能性がある 𝑅𝑒mそしてダイナモの停止。その後、マントル伝導の過程で、
FCMBS十分に増加すると、𝑅𝑒m再び超臨界状態になり、ダイナモが再起動します。コアが液相線以下に冷却されると、コアの凝固が始まります。これにより、軽元素(炭素、硫黄など)が放出されるため、コアダイナモの浮力源が追加され、ダイナモ発電の2回目の周期(または1回目/2回目の周期の延長)が発生する可能性があります。コアが完全に凝固すると、ダイナモ発電はできなくなります。
次のセクションでは、1D 球対称モデルについて詳しく説明します。まずマントル粘性モデルから始め、次に熱進化の各段階を説明し、最後に磁場生成と数値実装について説明します。モデルの仮定については、セクション4、5、6で説明します。

図1:微惑星の熱進化の段階を示す図。青(核)と紫(マントル)のラベルは、ステレンボルグとクロウリーのモデルと比較して、私たちのモデルで採用された重要な改良点を強調しています(2012); ブライソンら(2019a)およびDodds et al. (2021これまでのモデルでは、マントル対流の終了後、コアの凝固(ステージ 7)による磁場生成のみを考慮していました。しかし、私たちのモデルでは、コアの凝固前に磁場が 2 回発生する可能性を考慮しています。磁気レイノルズ数が臨界値を超えると、ステージ 4、6、7 で磁場生成が発生する可能性があります。初期のコアの硫黄含有量が低い場合、マントル対流が停止する前にコアが凝固し始め、ダイナモ生成が一時停止しない可能性があります(ステージ 5)。
2.2マントル粘性
マントル粘性は、マントル温度と溶融率の変動により、微惑星の熱進化中に何桁も変化し、マントルの冷却に大きな影響を与えます。マントル粘性は、対流中およびマントル対流から伝導への移行中のマントル境界層の厚さを制御し、CMB 熱流束とダイナモ生成に影響します。このモデルでは、温度によるレオロジー挙動の変化を捉えるために 4 つの粘性則を定義し、粘性則と対流パラメータ化が自己整合的であり、粘性パラメータの不確実性を反映するように完全に調整できることを保証します。

図2 :マントル粘性の温度変化(黒実線)
𝜂0 =10^19Pas、𝜙c =0.3、𝛽 = 0.0225K^−1 𝛼n =30、 そして𝜂𝑙 = 10 Pas。各パラメータの変化による影響は、色付きの矢印と線で示されています。水平軸の灰色の上部の目盛りは、マントルの固相線温度がそれぞれ 1400 K、液相線温度が 1800 K の場合の固相線以上の温度での等価溶融分率を示しています。
マントル粘性の温度依存性は、5つの制御変数(図2 )によって区分的に定義される:臨界溶融率、
𝜙c、アレニウスの傾き、𝛽、溶融弱化指数、𝛼n、固相線における基準粘度、𝜂0、液体の粘度、𝜂𝑙:

ここ𝑇m、sそして𝑇m、l
それぞれマントルの固相線温度と液相線温度である。𝑇𝜙𝑐は気温はΦcそして𝜂c=𝜂(𝑇𝜙𝑐)粘度は𝜙c
は式1bで計算されます。溶融率、
𝜙
線形液相線近似を仮定して計算されます。
𝜙=𝑇−𝑇m,s/𝑇m,l−𝑇m,sマントルの組成は指定せず、同じ珪酸塩固相線を仮定する。
𝑇m,s=1400 K、液相線、𝑇m,l=1800 K、Bryson et al. の値(2019a)およびDodds et al. (2021)(第5.1節参照)。マントルの固相線と液相線は圧力に依存しない定数である。これは微惑星マントルの圧力変化が小さいためである(<50MPa)。
固相線以下では、粘度はアレニウス温度依存性を持つ(式1a)。この依存性は、基準温度におけるフランク・カメネツキー近似を使用してモデル化される。
𝑇ref、および基準粘度、𝜂0、E/𝑅𝑇≈E(𝑇−𝑇ref)/𝑅g𝑇ref^2 = 𝛽(𝑇−𝑇m,s)、 どこ
Eは活性化エネルギーは
𝑅g = 8.31JK^−1mol^−1
は気体定数であり、マントル固相線が基準温度とされる(Frank-Kamenetskii、1969)固相線より上で、臨界融解率より下では、この運動学的アレニウス依存性は、さらに融解弱化依存性を持つ。
αn𝜙=𝛼n𝑇−𝑇m,s/𝑇m,l−𝑇m,s (式1b)。粘度は急激に低下し、
𝜙c溶融物が残りの固体相を囲み、物質が分解するためである。
𝜙c粘性はクリーガー・ドハティ関係式(ファロウギとフーバー、2015; スターツら、2022)(式1d)は、溶融分率が1に近づくにつれて液体粘度が一定になる傾向がある。
式1cは、dlog10𝜂/d𝑇 = Δ𝜂/w 粘度の急激な低下における数値安定性を確保するため
𝜙c。wは、この近似によってカバーされる領域の幅であり、近似領域を最小限に抑えながら数値安定性を確保するために 5 K に設定されています。
Δ𝜂 = log10(𝜂(𝑇𝜙𝑐+w))−log10(𝜂(𝑇𝜙𝑐))粘度の対数差は𝜙c、式1bで決定され、粘度は𝑇𝜙𝑐+w 式1dによって決定される。
アレニウス温度依存性(式1a)は粘性温度スケールを決定する。
Δ𝑇/∱rh 対流を制御する対流領域全体の温度差の割合を決定する(ミショーとノイフェルド、2022; ダヴァイユとジョパール、1993)

この定義では、𝑇m 対流領域(マントル)の温度であり、
Δ𝑇 内部と境界面(マントルの場合)の温度差である。
Δ𝑇=𝑇m−𝑇𝑠)。
Brysonらの3ピースモデルと比較すると、2019a)このモデルは数値安定性を近似した領域が1桁狭いため、
w、そしてクリーガー・ドハティの関係を粘度に適用する。
𝜙c定数値を想定するのではなく、タンDodds らが採用した近似値(2021)は、固相線での傾きの変化を捉え、粘性率の勾配が急である。
𝜙c
物理的に意味のあるパラメータを使用して調整できます。
2.3蓄積
私たちのモデルは、特定の時間に200 Kでケイ酸塩とFe-FeSの未分化混合物が瞬間的に集積することから始まる。
tacc、CAI形成後。微惑星表面の熱流束の範囲は十分に小さいため、平衡表面温度への影響は無視できるため、シミュレーション全体を通じて微惑星表面温度は平衡温度200 Kに固定されています(<10 K; ドッズら、2021)植物胚中心では、∂𝑇/∂𝑟𝑟=0 = 0シミュレーション全体を通して。
2.4差別化前
集積後、微惑星は26Alそして60鉄の放射性崩壊により熱くなり、熱はまず伝導によって体内を運ばれる。

どこ𝜌密度はC𝑝比熱容量は𝑇温度は𝑟半径は𝑡時間であり、kは熱伝導率です。下付き文字chは未分化コンドライト物質の値を表します。未分化微惑星はケイ酸塩マントルと同じ熱特性を持つと仮定されます(例:Elkins-Tanton et al.、2011; ブライソンら、2019a)は、密度を除いて、微惑星の嵩密度を使用する。微惑星の分化前の圧縮と焼結は無視され、一貫して一定の熱拡散率が使用される。なぜなら、これらのプロセスは、微惑星が最初に200 Kから700 Kに加熱されるときにのみ微惑星に影響を与えるからである(Yomogida and Matsui、1984)であり、全体的な熱の進化に最小限の影響しか与えません。
𝐻単位質量あたりの放射加熱力である

どこ𝐻i、0同位体の単位質量あたりの加熱力である
ICAI設立当時、fi最も一般的な安定同位体に対する放射性同位体の豊富さの比率である。
Xiは、集積物質中の元素存在比(重量%)であり、𝑡1/2,iは放射性同位体の半減期である。各パラメータに選択された値は表1にまとめられている。微惑星が加熱されるにつれて金属とケイ酸塩が融解することは、修正された比熱容量(Merk et al.,2002; ドッズら、2021(金属とケイ酸塩の混合物)
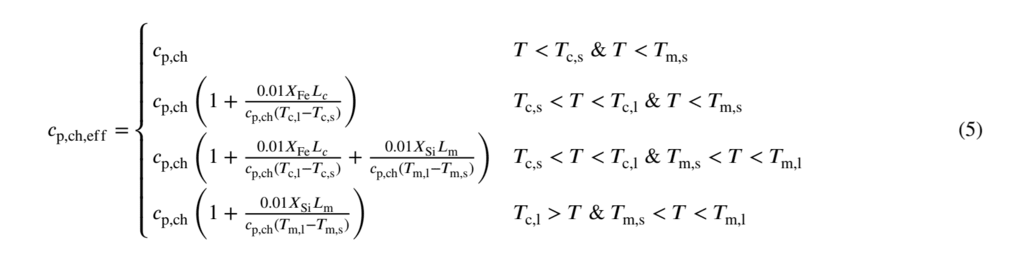
ここX鉄そしてXsiは、付着物質中のFe-FeSおよびケイ酸塩の割合(重量%)である。
LcそしてLm Fe-FeSとケイ酸塩の融解潜熱である。
𝑇c、lそして𝑇m、l Fe-FeSとケイ酸塩の液体であり、𝑇c、sそして𝑇m、s
Fe-FeSとケイ酸塩の固相線である。Fe-FeSとケイ酸塩の溶融分率は、両方とも線形液相線近似を使用して計算される。Fe-FeS系の硫黄含有量は、入力パラメータとして設定される。共晶Fe-FeS組成の微惑星の場合、微惑星の温度がFe-FeS固相線に達すると、すべてのFe-FeSが溶融するまで温度は固定される。このシナリオでは、Fe-FeS溶融分率の時間変化は、
𝜙鉄は、式3の左側の項を次のように置き換えることによって計算されます。
𝜌chX鉄L鉄∂𝜙鉄/∂𝑡どこ𝜌chX鉄
未分化物質中の Fe-FeS の密度です。
固体の停滞蓋対流(セクション2.5.2)は、分化の前に、天体が加熱されるにつれて始まる可能性がある。この対流モードでは、停滞蓋は、厚さ10nmの微惑星の表面にある導電性の不動境界層である。
𝛿0(式7)そして蓋の下の内部は対流する(図3)。微惑星内の圧力変化は断熱温度勾配を無視できるほど小さいため、内部は等温であると仮定される。内部温度は、𝑇iに従って進化する

どこFlid = −Kchd𝑇/d𝑟|𝑟=𝑅−𝛿0、Vi内部の容積であり、Alid停滞した蓋の底の表面積である(ソロマトフ、1995)。 停滞した蓋は、内部と蓋の放射性元素の量が等しいと仮定すると、式3に従って熱を輸送し続け、微惑星が加熱されるにつれて厚さが減少する。 微惑星が対流している間に共晶Fe-FeSの溶融が起こる場合、式6の左辺は次のように置き換えられる。
𝜌chX鉄L鉄∂𝜙鉄/∂𝑡固体の停滞したlidの対流は、𝛿0微惑星の半径の99%未満である。𝑅。
ケイ酸塩溶融分画が𝜙臨界溶融率に達すると、𝜙c、ケイ酸塩の粘度が急激に低下し、レインアウトによって分化が進行します。レインアウトでは、より密度の高い溶融Fe-FeSが、ストークス沈降によって密度の低い低粘度のケイ酸塩に沈降します。このプロセスは迅速です(10^4ミリメートルサイズの液滴の場合(S5を参照)であり、瞬間的に近似することができる。
𝜙=𝜙cこの過程の時間スケールの不確実性のため、この温度は無視される(セクション4およびセクションS5を参照)。内部圧力勾配が小さいため、物体はほぼ等温であり、単純化のため、微惑星全体が同時に分化すると仮定する。我々のモデルでは、分化前にすべてのFe-FeSが完全に溶融し、核は最初は液体であると仮定する。この仮定を満たすためには、Fe-FeSの初期核硫黄含有量の液相線温度は、
𝜙cこれにより、初期のコア硫黄含有量の範囲が制限されます(セクション4.3.1を参照)。
分化の時点で、物体は瞬時にFe-FeS核を形成し、その半径は物体の半分であると想定される。
𝑟𝑐=𝑅/2、その上にケイ酸塩マントルが重なる(図3)。核とマントルは臨界溶融率の温度で等温であり、
𝑇𝜙c鉄はすべて核に分配され、アルミニウムはすべてマントルに留まると仮定する。これにより、
26Alマントルと60鉄初期状態と比較したコアの硫黄含有量。初期コアの硫黄含有量は、XS、0
は入力パラメータによって設定され、未分化微惑星中の Fe-FeS の硫黄含有量と同じです。
2.5分化後
2.5.1クラスト
地殻の存在は、固定表面温度境界条件に簡略化されています。表面ノードのみが、微分化できるほど高温になりません。したがって、多孔質レゴリスの厚さはこのモデルの解像度を下回るため、無視されています(セクション4.2)。
2.5.2マントル

図3 :対流するケイ酸塩マントルと対流するFe-FeSコアのモデル設定を示す概略図。コアとマントルは結合した2つの貯留層です。地殻は固定された表面温度で近似されます。
𝑇𝑠 = 200 K. 赤い線は微惑星の温度プロファイルで、温度は右に行くほど高くなります。この図では、マントルは停滞した蓋の領域で対流しています。内部は等温で、CMBには伝導境界層があります。
𝛿𝑙、そして表面、𝛿0黒い破線は停滞したlidの底部を示しています。核にはCMBに熱境界層があり、
𝛿𝑐マントルとコアが伝導性である場合、代わりに各層全体に温度勾配が存在する。CMB熱流束のバランス(FCMBS、m = FCMBS、c)はCMB温度を計算するために使用される𝑇CMBS
記号の意味はセクション2.5.2と2.5.3に記載されています。
マントルは伝導または停滞蓋対流によって熱を輸送する。停滞蓋対流では、マントルは等温の対流内部を持ち、表面の下に伝導境界層(「停滞蓋」)があり、CMBの上にもう1つあると想定される(図3)。我々が採用したパラメータ化では、停滞蓋の厚さには蓋の底部の薄い可動境界層が含まれる(セクションS1.2.2を参照)。停滞蓋の厚さについては経験的に決定された式を仮定する。
𝛿0、内部加熱、上部境界と下部境界での熱流束、温度依存粘性、および自由滑り境界条件(DeschampsとVilella、2021)


図4 :コア上部の不安定層の対流混合によるコア熱成層の侵食の概略図。赤い線は温度プロファイルを示し、温度は右に向かって上昇します。赤い破線は対流に対して不安定なコアの部分を示します。図の上部は、マントル内のCMB境界層の上にある対流マントルの基部です。
𝛿𝑙、そして核内のCMB境界層、𝛿c
時間は左から右へ進む(a–c)。破線はマントルとコアのCMB境界層を示す。コアのCMB境界層(下の破線)は、コアが対流しているときにのみ存在する。コアの熱成層は、マントルの冷却(マントルの温度プロファイルをコアのそれに対して左にシフトさせる)または加熱によって侵食される。
60鉄コア内(マントルに対してコアの温度プロファイルを右にシフトさせる)。すべての記号はセクション2.5.3で定義されています。

図5 :コア凝固の形状を示す概略図。凝固材料の量は次のようにパラメータ化されます。
𝑟i(マゼンタの線)対流の長さスケールは次のように表される。
𝑙=𝑟1−𝑟2
微惑星核の固化のメカニズムの不確実性を考慮するために、2つの端成分形状を考察する(図の中央のシナリオは中間の形状も示している)。1つの端成分では、mfrac = 0では、コアの安定した固体部分はCMBから内側に向かって成長します。もう一方の端成分では、mfrac =1の場合、固まった鉄はすべて再溶融せずに落下し、集積した内核を形成します。
mfrac = 0では、対流の長さスケールはコアが固まるにつれて最もゆっくりと減少し、mfrac =1 の場合、対流の長さスケールは最も速く減少します。微惑星コアの固化のメカニズムが不確実であるため、各シナリオで対流がどのように駆動されるかを規定せず、長さスケールの変化のみに焦点を当てます。両方のエンドメンバーで、固化領域の固体分率は 100% であると仮定します。詳細と議論については、セクション2.5.4と6.1を参照してください。
7見通し
私たちのモデルには、以前のモデルでは無視されたり単純化されたりしていたいくつかの物理的および化学的特徴が含まれています。たとえば、私たちの微惑星熱進化モデルは、マントル対流も含むマントル微惑星の非共晶核凝固をモデル化した初めてのモデルです。統一された浮力フラックスを計算することで、同じスケーリング則を使用することができます。
𝑅𝑒m熱の進化を通して磁場の強さと熱対流の同時発生を可能にする。さらに、
60鉄コアの熱構造に、対流の段階的な停止と境界層の厚さをモデル化するために、マントル対流のパラメータ化を調整することも選択しました。これは、表面冷却と内部加熱を伴うシステムに適用できます。マントル粘性関数に物理的に現実的な値を実装し、粘性関数に追加の部分を追加して、温度の関数として粘性挙動の全範囲を捉えるようにしました。マントル粘性の変化に反応するように、停滞蓋スケーリング則も実装しました。これにより、将来の研究では、特定のサイズと組成の微惑星に最も適した粘性パラメータを選択できるようになります。モデルの他のパラメータは完全に調整可能であり、特定のパラメータの影響に関する将来の研究や、隕石の古地磁気記録の解釈を可能にするために特定の隕石母天体に適用することができます。別の研究では、マントル粘性、原始的粘性、および原始的粘性係数を体系的に変化させます。
60鉄/56鉄、初期の核硫黄含有量、微惑星のサイズなど、これらのパラメータがダイナモ生成に与える影響についてより深く理解し、隕石の古地磁気記録に対する私たちのモデルの意味を理解するために、研究が進められている(Sanderson et al.、2024)。
部分的な分化と地殻形成を組み込むことで、モデルに若干の改善を加えることができます。また、2 つの重要な改良点があります。まず、微惑星の分化のメカニズムと初期の核の硫黄含有量を調和させる必要があります。微惑星の核が最初は硫黄含有量の低い状態で形成されるか、または後に硫黄を失うか、そしてこれらの要因が核の固化とダイナモ生成の開始にどのような影響を与えるかについては、さらに研究する必要があります。次に、マントルに包まれた微惑星の核の内側への固化の考えられるメカニズムと、これがダイナモ生成に与える影響について、さらに詳しく調査する必要があります。
8結論
微惑星は太陽系形成後の最初の数百万年間に形成され、その多くが地球型惑星に集積しました。熱進化およびダイナモ生成モデルは、これらの微惑星の内部構造と熱履歴に関する洞察を提供します。ただし、以前のモデルはダイナモ生成の初期または後期のいずれかに焦点を当てていたため、完全な磁場履歴を予測する能力が制限されていました。私たちのモデルは、マントル対流の記述と非共晶コアの凝固のパラメータ化に焦点を当て、微惑星の熱進化とダイナモ生成に関する統一された、より汎用性の高いモデルを提供します。具体的な機能強化は次のとおりです。
• 放射性加熱による60鉄コアの中に。
• マントル対流のパラメータ化と自己整合し、マントル粘性の影響を調査するために調整できるマントル粘性モデル。
• 境界熱流束と内部加熱と一致する停滞蓋と CMB 境界層のパラメータ化。
• 停滞蓋とCMB境界層の厚さの合計がマントルの厚さよりも大きい場合の対流の停止。
• 磁場生成を促進するための統一された熱および組成浮力フラックスを備えた非共晶コア凝固のパラメータ化モデル。
• ダイナモ生成の期間における磁場強度の計算。
私たちのモデルに実装されたこれらの変更の主な結果は、半径 500 km の微惑星に対して生成された磁気履歴の例によって実証されています。以前のモデルと比較すると、次のことがわかります。
• 核熱成層はより急速に侵食されます。
• マントル対流とダイナモ発生の最初の時代がより長く続きます。
• コアの固化により双極子場の強度はわずかに増加しますが、マントル対流の停止後に追加の浮力源を提供することで、ダイナモの持続時間に対するより強力な制御が行われます。
• ダイナモ生成の第二期は、コアの固化によって引き起こされるものではありません。
私たちのモデルは、組成ダイナモと熱ダイナモの両方の磁場強度を持つ微惑星の完全な磁場生成履歴を予測できます。したがって、このモデルは、微惑星のダイナモ生成の一般的な制御を理解し、隕石の母天体の古地磁気記録からその特性に関する制約を回復するための強力なツールとして機能する可能性があります。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます