太陽系外惑星系のエネルギー最適化：そっくりの双子から暴走成長への移行

ガス惑星の胎児は連惑星から始まって暴走成長する説です。以下、機械翻訳。
太陽系外惑星系のエネルギー最適化：そっくりの双子から暴走成長への移行
（2020年2月25日に提出）
観測された太陽系外惑星のサンプルに見られる傾向に動機付けられて、この論文は惑星系を形成するための潮汐平衡状態を決定します---角運動量、一定の総質量、および固定軌道間隔の保存を条件とします。低質量の制限では、次数mの質量を持つ超地球クラスの惑星に有効p〜10 M⊕、以前の研究では、エネルギーの最適化がほぼ等しい質量の惑星になり、円軌道が平面に限定されることが示されました。現在の治療は、惑星体の自己重力を含めることにより、以前の結果を一般化します。総質量mが十分に大きいシステムの場合T惑星では、最適化されたエネルギー状態は、ほぼ等しい質量の惑星の場合から、1つの惑星がほとんどの物質を含む構成に切り替わります。この遷移は、約mの臨界質量しきい値で発生しますT≥ メートルC〜40 M⊕（値は、惑星軌道の半長軸、星の質量、およびその他のシステムプロパティに依存します）。これらのエネルギー最適化の考慮事項は、連星から惑星系、太陽系の巨大惑星を周回する衛星の集まりまで、広範囲の質量スケールに適用されます。
キーワード：惑星系—惑星と衛星：動的進化と安定性
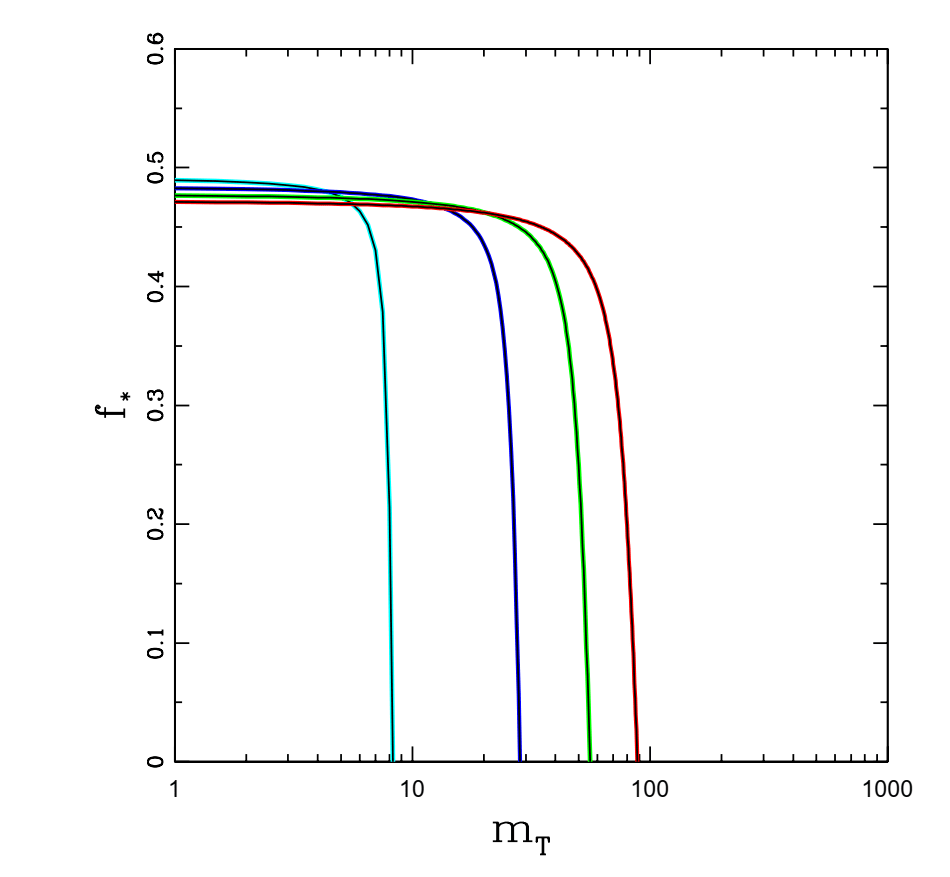
図1.惑星ペアの総質量mTの関数としての（内惑星の）質量分率fの最適化された値（in　M⊕の単位）。 明確にするために、恒星質量M ∗ = 1M、半長軸a2 = 0.1 AU、および惑星半径Rp
= 3R⊕。 4つの曲線は、軌道間隔パラメーターの異なる値Λ= 1.25（シアン）、1.5（青）、1.75（緑）、2.0（赤）、図の左から右へ。 総質量mTとして増加します。f〜1/2からf→0への比較的急激な遷移に注意してください。


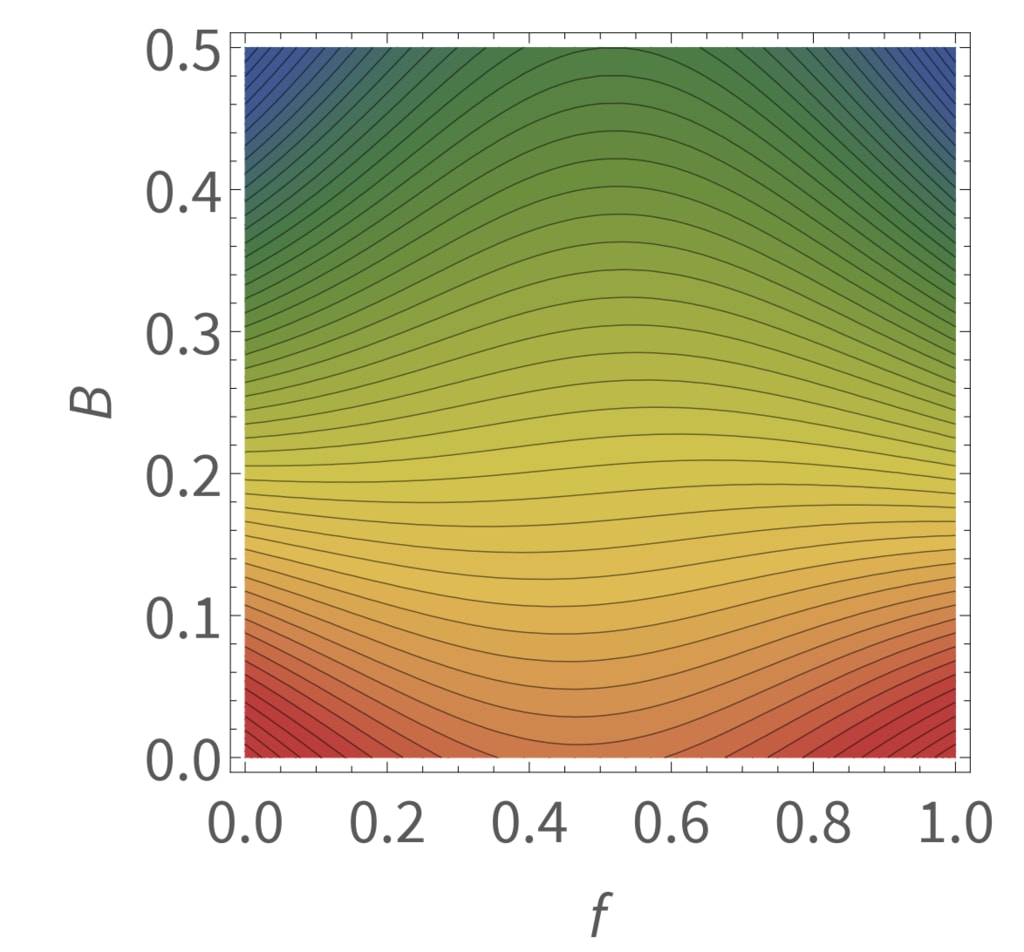
図2.質量分率fと指定する無次元パラメーターBの関数としてエネルギーを示す等高線図
惑星の自己重力の相対的な重要性。 軌道間隔パラメーターΛ=2。定数の等高線は
Bの値が小さい場合、エネルギーは上に凹になり、f〜1/2に近い最適値になります。 対照的に、輪郭は凹面です
Bが大きくなると、f〜0およびf〜1が優先されます。


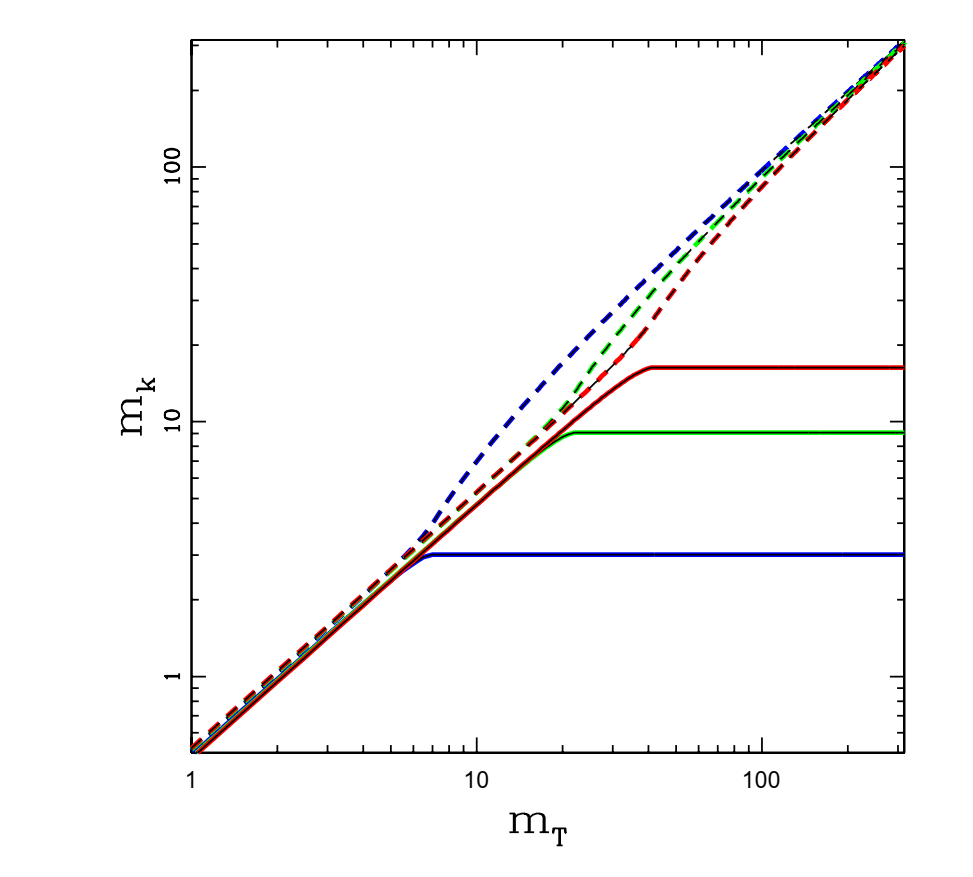
図3.総質量mTの関数としての、惑星ペアの2つのメンバーの質量mk。
時間とともに増加します。 すべての質量はM⊕で与えられます。 実線の曲線は、内側の（より小さい）惑星の質量を示していますが、
破線の曲線は、外側の（より大きな）惑星の質量を示しています。 の3つの値の結果を示します軌道間隔パラメーターΛ= 1.25（青、左）、1.5（緑、中央）、および1.75（赤、右）。


図4.太陽系外惑星系で見つかった惑星対の観測されたサンプルの質量分率fの分布
Np> 3メンバー。 青いヒストグラムは、総質量mT =の低質量惑星のペアの正規化された分布を示しています
m1 + m2 <40M⊕。 赤いヒストグラムは、mT = m1 + m2>40M⊕の高質量惑星の対応する分布を示しています。
エラーバーは√を表しますNエラー。 2つの分布は明らかに異なります。


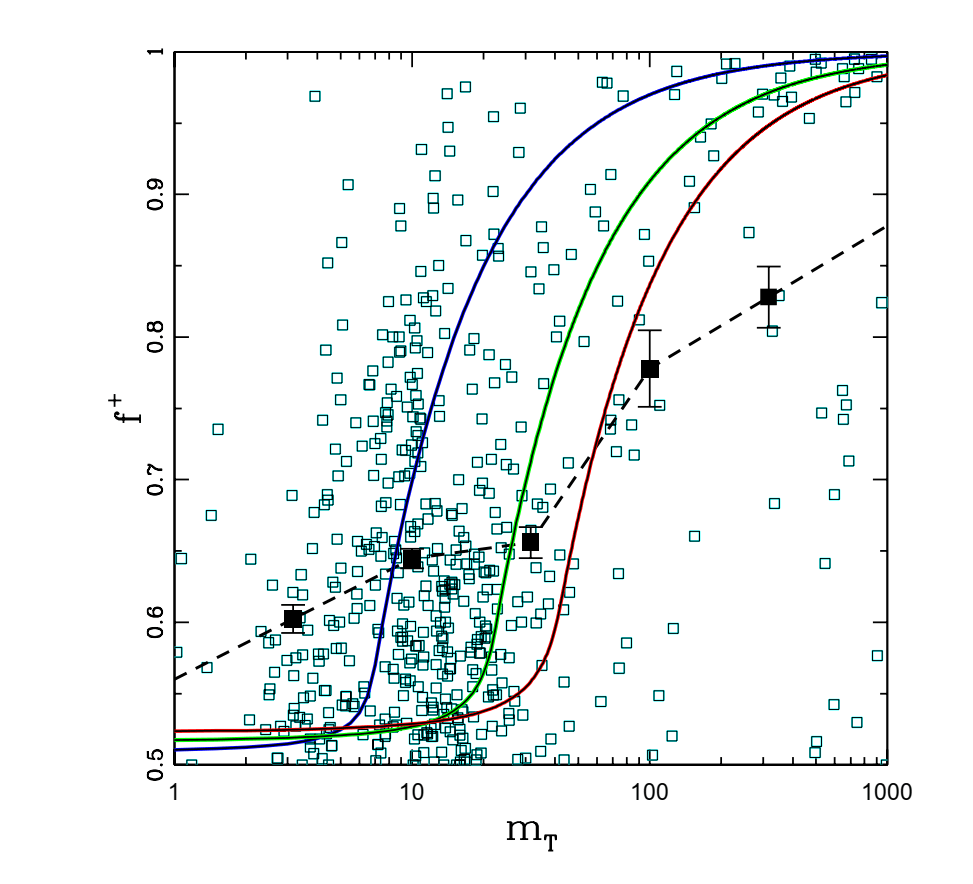
図5.質量分率f　惑星ペアの総質量mTの関数としての最大惑星の+。 代替質量分率f
+はfであると定義されます　+ = fは、内側の惑星の質量が大きく、f+ = 1 − f外側の惑星が重い場合。 の
開いたシアンの四角は、観測サンプル内のすべての惑星ペアの質量分率を示しています。 固体の黒い四角
エラーバーには、同じデータのビン分割されたバージョンが表示されます。 ビン分割されたデータポイントを結ぶ破線は、
低質量および高質量。 実線の曲線は、理論的に予想される質量分率f+、進化シナリオに基づいて
前のセクションの3つの値の軌道間隔パラメーターΛ= 1.25（左、青）、1.5（中、緑）、および1.75（右、赤）。 データには大きなばらつきがありますが、質量分率f
+は、全惑星質量mTの増加関数です。特にmT>〜40M⊕については、この論文の予想とほぼ一致しています。