彗星と惑星状天体形成

素人にも分かりやすいように図入りの開設を期待したのですが数式優先でした。www.DeepL.com/Translator（無料版）で翻訳しました。
彗星と惑星状天体形成
この章では、惑星状天体や彗星の形成過程について概説する。ガスとダストの相互作用がどのように媒介されるかを説明する。
次に、様々な惑星状天体形成のモデルに入り込み、これらの
その結果、どのように惑星状物質が形成され、どのような構造をとるのかを説明する。その際、惑星状天体形成の2つのパラダイムに焦点を当て、比較する。
すなわち、過剰な粒子密度の重力崩壊（これは様々なメカニズムによって生じうる）と、粒子の成長による惑星状体の形成である。
また、衝突や重力による凝集を経て、粒子が成長してプラネテシマル（惑星状天体）になる。
最後に、これらのモデルによる予測を、Rosetta, New Horizonsミッションによって得られたデータ、および遠方のKuiper衛星の観測によって得られたデータと比較する。
遠方のカイパーベルト天体の観測で得られたデータと比較する。
1. はじめに
サブミクロンの小粒から惑星状物質の形成は、約10-12桁のスケールアップと多数の物理過程を内包している。
また、粒子と粒子の付着からディスクガスと固体粒子の角運動量交換に至るまで、多くの物理過程が存在する。一方
これらの物理過程が具体的にどのように作用するかについては、多くの未解決の問題がある。
近年、いくつかの重要な問題に対する解決に大きな進展が見られる。
1.サブミクロンサイズの粒がどのように成長し、これまで観察されてきたmm-cmサイズの固体（ペブルと呼ばれる。
より完全な定義については2.5を参照）、どのように成長するのか？
2. 2. 小石はどのようにして成長を続け、kmサイズの惑星状物質を形成するのか？
3. 3. 惑星状物質がどのような性質を持つのか？
3.できあがった小惑星はどのような性質を持っているのか、また、太陽系小惑星の観測結果と比較すると
彗星やカイパーベルト天体などの太陽系小惑星の観測結果と比較する。
カイパーベルト天体(KBO)などの太陽系小天体観測と比較してどうなのか？
理論的な面でも、多くの新しい知見が得られています。
が得られている。特に、解析技術と数値シミュレーションの強力な組み合わせにより
特に、解析的手法と数値シミュレーションの強力な組み合わせによって
多くの不安定性（例：Youdin and Goodman 2005; Youdin 2005）とメカニズム（例：Cuzzi et al.2008; Hopkins 2016) が明らかにされている。
重力崩壊して惑星状物質となるのに十分な密度の領域に小さな粒を集中させることができる機構（例：Cuzzi et al.
を発見した。
これらの技術は、現在および将来の観測キャンペーンで検証可能な予測に直結しています。
また、この分野では、観測データも豊富である。
観測データも豊富である。小惑星への多くのミッション（例：OSIRIS-REX,Rosetta、New Horizons）、太陽系小天体へのミッション（e.g,Stern et al. 2021) や、太陽系外縁部のような小天体集団の大規模サーベイなど
太陽系外縁部探査（OSSOS）のような小天体集団の大規模調査も行われ、太陽系惑星の物理的特性について多くの新しいデータが到着している。
太陽系微惑星の物理的特性について、多くの新しいデータが届いています（例,Kavelaars et al. 2021; Fraser et al. 2021)。さらに
次世代光学・赤外線・電波望遠鏡の登場。
アタカマ大型ミリ波サブミリ波干渉計(ALMA)や超大型電波望遠鏡(VLBI)
(ALMA)や超大型望遠鏡(VLT)などの次世代光学・赤外線・電波望遠鏡の登場により、近傍星周辺の惑星形成円盤におけるガスと小粒子のダイナミクスに対する我々の理解は革命的なものとなっている
(ALMA Partnership et al. 2015; Isella et al. 2016; Huangら 2018）。
最後に、実験室での実験が非常に実り多いものであった
異なる組成の固体粒子が衝突したときにどのように相互作用するかを正確に調べる上で、実験室実験は非常に有益であり、したがって
観測的研究、理論的・数値的研究の両方を強力に補完するものです（Blum and Wurm 2008）。さらに
また、異なる仮説のメカニズムで形成されたプラネテシーマの物理的性質も実験室で研究されている（Blum 2018）。
実験室で研究されており（Blum 2018）、太陽系の最も原始的な天体の物性と比較することが可能である。
との比較が可能である。


実際、理論、観測、実験室での研究を組み合わせることで、惑星や彗星の形成に関する理解を深めることに成功しています。
惑星状天体や彗星の形成に関する理解を深めるのに、大きな成功を収めています。この章で
この章では、そのような研究をレビューし、どのように惑星状小惑星が生まれるかについての最新の理解を詳しく述べる。我々のアプローチは
教育的なアプローチであるため、惑星状天体形成の物理学に焦点を当てることになる。
惑星状天体形成の物理そのものに焦点を当てる。
観測や実験と関連づけながら解説する。
2. ダスト・グレインの成長
このセクションでは、原始惑星系円盤の中で小さな固体がどのように成長するかについて、現在の理解を詳しく説明する
(PPDs)において、どのように小さな固体が成長するかについて、現在の理解を詳しく述べる。ダストの成長に関するいくつかの議論は
第2章で、相川らによって議論されている。
を制限する過程について詳しく述べる。
しかし、ここではその詳細について説明し、mm-cmサイズを超える小さな粒の成長を制限するプロセスについて述べる。
3 章で説明する多くのメカニズムの舞台となる。
PPD中の固体の進化は、多くの影響を受けている。
しかし、それらは大きく分けて、1) 固体の組成、サイズ、形態の進化、2) 原始惑星系円盤内での輸送とダイナミクスの2つの領域に分けられる。この2つの分野は、互いに多くの影響を及ぼし合うため、一方を他方から切り離して扱うことはできないことを認識することが重要である。
この2つのカテゴリは多くの点で互いに影響し合っている。
粒子の構成、サイズ、形態はその空気力学的特性に影響を与え、空気力学的特性は粒子が原始惑星系でどのように輸送されるか
空力特性は、粒子が円盤内をどのように移動し、その過程で環境がどのように変化するかを決定する。
環境がどのように変化するかを決定する。環境は
その結果、衝突や組成がどのように変化するかが決定される。
衝突速度の設定（例えば、Birnstiel et al.2016参照）や凝結・昇華速度（例えば、Stammler et al.2019). 以下では、ダスト
がどのように輸送され、衝突によってどのように進化するかを説明し、それらの側面が互いにどのように影響するかを強調する。
これらの側面がどのように互いに影響し合っているかを強調する。
まず、小さな粒から粒子への進化を説明するために重要な量である
を説明するのに重要な量、すなわち粒子停止時間を紹介することから始めます。これは、以下のような時間スケールで定義されます。
粒子速度が抗力によってガス速度に順応する時間スケールと定義される。
と定義され、次のようになる。
tstop = m ∆v / Fdrag = a ρs/ ρgvth , (1)
ここで、m, a, ρs, ∆v, vth は粒子の質量、半径、物質密度、ガスとダストの速度差の絶対値、平均熱速度である。
は粒子の質量、半径、密度、ガスとダストの速度差の絶対値、ガスの平均熱速度である。
ガスの平均熱速度(ガス音速と係数
である。式(1)の右の等式は
は、抗力がEpstein領域 (Epstein 1924; Weidenschilling 1977) にあると仮定し、粒子径がガス分子の平均自由行程より小さく、かつ
さらに、ダスト粒子は球状で非フラクタルであるとする。多くの場合、停止時間はストークス数
数1
St = tstop - Ω, (2)
で表されることが多い。
で表される。このようにストークス数は無次元数であり
は粒子の空気力学的挙動を指定する無次元数である。ストークス数は
ストークス数は、「無次元粒子径」ともいえるし、「無次元粒子径
無次元粒子径 "と見なすことができ、また、無次元停止時間と呼ばれることもある。
St 1を持つ粒子は、気体の流れに対して、軌道上の粒子よりもはるかに速く結合するため、無次元停止時間
St 1の粒子は軌道時間スケールよりもはるかに速くガス流と結合し、St 1の粒子は結合するのに多くの軌道を必要とする。
粒子の系統的なドリフト運動を引き起こすのはこの抗力による結合であり(Whipple 1972; Nakagawaら1986)、乱流による粒子の影響を決定し(Voelkら1980; Ormel and Cuzzi 2007)、また、半径方向のガス流の強さを決定するのは、この抗力による結合である。
半径方向のガス流がどの程度強く粒子を引き寄せるかを設定し
(を設定する（Takeuchi and Lin 2002）。以下では、これらの力学的効果について
これらの力学的効果についてより詳しく説明する。
2.1. 鉛直方向の沈降
傾斜軌道上の粒子(ガスがない場合)
は垂直座標を原点とする基準面の上下に振動している。
鉛直座標が原点となる基準面（以下
これ以降、円盤の「中平面」と呼ぶことにする。このことは
このことは、中平面近傍の粒子の運動方程式からわかる。
中平面付近の粒子の運動方程式からわかる（Nakagawa et al,）
z¨ + z Ω^2 + z˙ / tstop = 0, 　　　　　　(3)
ここで、最初の2項は調和振動子を表す。
残りの項は、速度に依存する抗力項である。
このように、ガス円盤の存在によって、粒子が上下に移動すると
がガス中を上下に動くと減速する。
粒子の垂直運動は減衰した調和振動子とみなすことができる。
は減衰した調和振動子であるとみなすことができる。St 1の粒子は
の粒子はガス速度にすばやく適応し、この極限では粒子は振動せず、その速度はここではガス垂直速度にすばやく傾く
になる。このとき
このとき、重力の鉛直成分によって粒子は正中面へ加速され、粒子速度は高さ依存の重力と鉛直成分との間の
に近づき、高さ依存の重力加速度と速度依存の減速度の間で定常状態になる。数回の停止時間で
この平衡状態(z¨ = 0)に達するのは、数回の停止時間の後である。
の終端速度に達する。
vsett = -z Ω St (St 1の場合)となる。　　　　(4)
これは、羽根を落とすとすぐに等速になることに似ている。
の速度に達する。
このまま垂直方向の沈降が進むと、すべての粒子は土星の輪のようなカミソリのような薄い円盤状に中間面に集積することになる。しかし
しかし、現在のPPDの散乱光画像では、そうなっていない。
の散乱光画像が見事に描き出している（例：Avenhaus et al.2018）。
何らかのガス運動（バルクフローもあり得るが、おそらく垂直拡散性乱流）が働いていると考えられ
が作用し、粒子を垂直方向に混ぜ合わせることができると考えられている。
と考えられる。この場合、沈降が塵埃の濃度勾配をもたらすとバランスがとれ
この場合、沈降によって塵埃の濃度勾配が生じ、その結果、拡散流束が等しくなり、バランスが取れる。
拡散流束が発生し、沈降流束と等しくなるが、逆向きになる。
ρd vsett - D ρg ∂ρd/ρg/ ∂z = 0, 　　　　　　　　　　　(5)
ここで、拡散流束は、ダストがρdとρgによって混合されるときに、組成の勾配を平滑化するために作用する。
このとき、拡散フラックスは、ダストが乱流ガスと混合し、よく結合しているため、組成の勾配を滑らかにするように働く。
乱流ガスとよく結合している。上式の解は、定常的な
ダスト分布
ρd(z) = ρd(0) ρg(z)/ρg(0) exp(∫^z0∨sett/D dz^0). 　　　(6)
シュミット数Scは、ガスとダストの拡散率の比である2
. St 1 の粒子はすべてガスの乱流渦に十分に結合している。
の粒子はすべてガスの乱流渦と十分に結合しており、Schmidt数
は実質的に 1 となる。Youdin and Johansen (2007) が示した。
で近似できることを示した。
. ガスが等温静水圧解に従うとすると、スケール高さHを持つガウス曲線
の等温静水圧解に従うとすると、正中面付近では、与えられたサイズの粒子の垂直密度プロファイルもまた
ガウス曲線に従うが、そのスケールハイトは
Hp = H√ α / (α + St) 　　　　　　　　　　　　　　　(7)
ここで、αは乱流を定量化したものである。αの歴史
αの歴史や様々な定義は長くなるので、本章では割愛する。
本章の範囲ではありません。さらに、ここで使用するαは、いわゆる「乱流粘性は、いわゆる "乱流粘性 "とは区別される。
Shakura and Syunyaev (1973)のいわゆる "乱流粘性 "とは区別されるべきである。後者は半径方向と方位方向の速度擾乱の相関に依存し, 乱流磁気応力を含んでいる.
前者は純粋な無次元乱流拡散パラメータであり, 例えば, Johansen
and Klahr (2005)やFromang and Papaloizou (2006)などで定量化されているような純粋な無次元乱流拡散パラメータである。我々の目的では
乱流が等方的であると仮定して、乱流拡散パラメータを定義する。
等方性であると仮定し、乱流拡散をα = δv2 / c^2s,3
ここで，δv と cs は乱流速度と音速である．
である．
このため、中間面におけるダスト／ガス比は、ストークス数 St > αの粒子で、次のように向上する。
ρd(0) / ρg(0) = Σd / Σg √St/α　+ 1, 　　　　　　　　　(8)
ここで、Σd/Σg はダストとガスのカラム密度の比である。


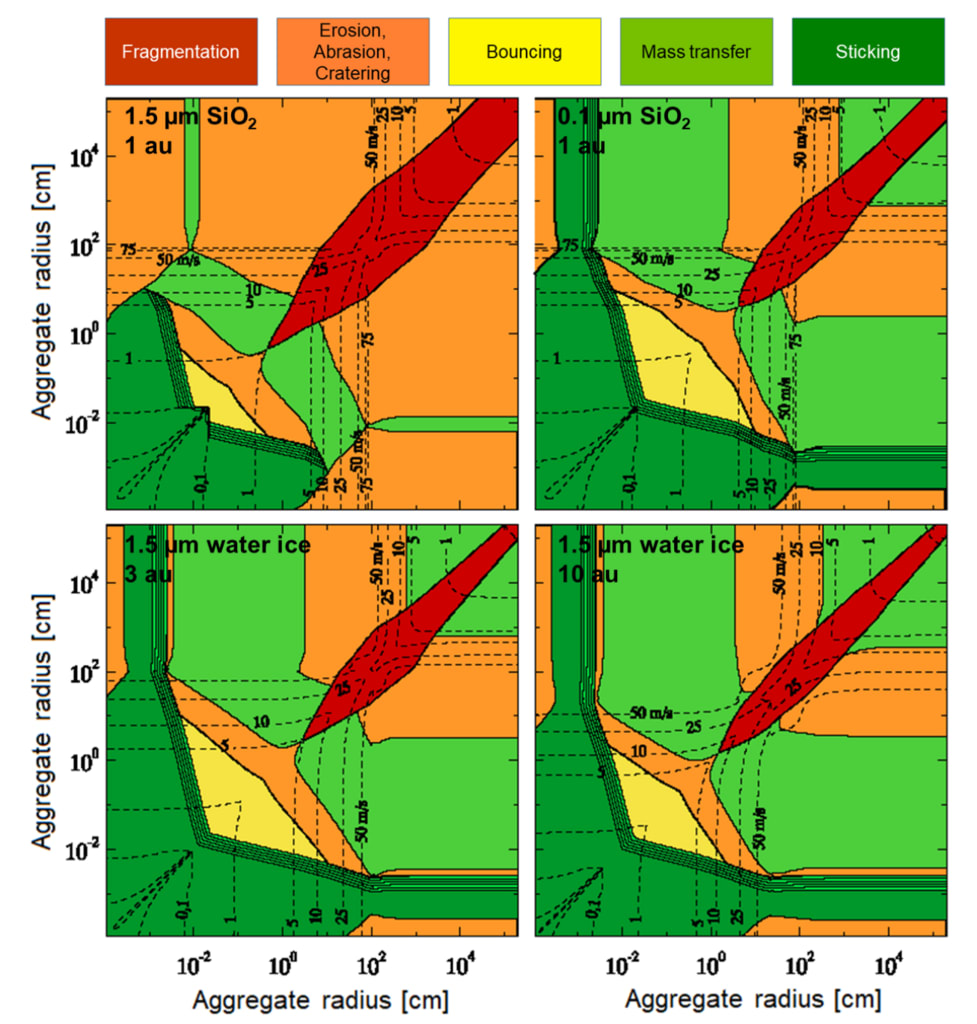
図1.- Kothe (2016)に倣った塵と氷の凝集体の衝突モデル。左上：SiO2 モノマーについて
1auで直径1.5μmのSiO2モノマー粒子、右上：1auで直径0.1μmのSiO2モノマー粒子、左下：3auで直径1.5μmの水氷モノマー粒子、右下：10auで直径1.5μmの水氷モノマー粒子に対応。
PPD の基礎となるモデルは、最小質量の太陽系星雲モデルである。画像提供：Stefan Kothe.


図2-フラクタル次元Df=2.0、1,024個のモノマー粒子からなるダスト凝集体のシミュレーション例。
粒径分布が非常に狭い1,024個のモノマー粒子からなる。


図3.- Birnstielら(2010)によるダストサイズ分布のシミュレーション結果
にならってシミュレーションしたもので、青の等高線で示す。灰色の矢印は
ドリフトと成長率を示す。成長限界は
を茶色/橙色（ドリフト限界）、紫色（フラグメンテーション限界）の線として表示した。
限界)の線として表示。灰色の線は対応する粒子のストークス
を示す。単分散成長/ドリフト軌道は黒の破線で表示。
で終了し、100kyr での位置を十字で示す。縦線は図4に示した粒径分布に対応する。図は Birnstiel et al.（2016）から引用した。


図4.図3のシミュレーションから3, 30, 100 auで測定したダストサイズ密度分布（対数質量あたりの表面密度）。
MRNサイズ分布の傾きと、トップヘビー指数(∝MRN)a^-2.5) を参考として示しています。図はBirnstiel et al.(2012).


図5.-ストリーミング不安定性の基本的なメカニズム。小さな塵の過密度（パネルA）は、抗力によってガスを内側に引き込む。
この内向きのガスの運動は、コリオリ力によって方位角方向に偏向される（パネルB）。過密の下流にすでに存在していた塵は
過密度の下流に存在する塵は、偏向したガスから抗力によって方位角方向の力を受け、下流の塵はより大きな半径で移動します。
その結果、下流のダストはより大きな半径に移動し（角運動量が増加したため）、元のダストの過剰密度に拍車をかけることになります。なお、この全体の
この全体のプロセスは、ダストの平均的な半径方向のドリフトに対応するフレームにあることに注意してください。(パネルC)。Squire and Hopkinsから変更(2020).

5. 結語
20年も前に、惑星系科学と天体物理学において、惑星縁辺の形成は最も大きな未解決問題の一つであった。しかし、この問題は依然として未解決であり、太陽系（および他の惑星）の形成を理解する上で最も重要である。
太陽系（および他の惑星系）の形成を理解する上で最も重要な問題であることは言うまでもありません。
この問題は未解決のままであり、太陽系（および他の惑星系）の形成を理解する上で最も重要な問題ですが、それ以来、多くの進展があったことは非常に喜ばしいことです。
それ以来、多くの進展があったことは、非常に心強いことです。
現在では、理論計算と実験によって、サブミクロン粒が小石サイズに成長する過程を詳細に理解することができ、さらに、小石がどのように形成されるかを説明する複数のモデルがあります。
小石がどのように次の段階に進み、惑星系を形成するのかを説明するモデルを複数持っています。
小石がどのように次の段階に進み、惑星状体を形成するのかを説明するモデルを複数用意しています。
もちろん、惑星系を包括的に理解するためには、解決しなければならない課題もあります。
の包括的な理解に向けて、どのようなメカニズムで
どのようなメカニズムで
どのようなメカニズムで形成されるのかを解明するためには、まだまだ課題があります。例えば、最大の論点は
例えば、最も大きな論点は、SIと重力凝集の両方に基づく理論モデルと観測結果の間にあるサイズ分布の不一致である。
例えば、最も大きな論点は、SIと重力凝固の両方に基づく理論モデルと観測値との間のサイズ分布の不一致である。他の重力崩壊メカニズム（例えば、SGI）はもっと良い一致を示すのだろうか？
のだろうか？それとも、少なくともSIシミュレーションにおける不一致は、より単純な何かの結果なのだろうか？
関連するパラメータをより広範囲に調査した結果なのか
それとも、少なくともSIシミュレーションでは、関連するパラメーターをより広範囲に調査したり、SI計算で数値的に制限されたスケールを下回るような、より単純な結果なのでしょうか？
しかし、このような未解決の問題があるにもかかわらず、以下のことが指摘されている。
重力崩壊のパラダイム、特にSIによる崩壊モデルが
特にSIによる崩壊モデルが正しいことを示唆している。
の一つである。ロゼッタ計画で得られた小惑星の熱的・構造的特性は、まさに小惑星の重力崩壊モデルを支持するものである。
惑星状天体形成の重力崩壊モデルを支持している。さらに、SIシミュレーションと観測の間でKBO連星系の性質が見事に一致していることは
SIが惑星系惑星の形成機構であることを強く支持している。
また、SIシミュレーションと観測結果の一致は、惑星状天体形成のメカニズムとしてSIを強く支持し、重力凝固モデルを強く否定しています。
さらに、数値モデルの改良と計算機資源の利用が容易になれば、この問題の理論的な側面は、今後ますます重要になると思われる。
この問題の理論的な側面は、今後数年で大きく進展すると思われる。
この問題の理論的側面は、今後数年のうちに大きな進歩を遂げるだろう。これらの進歩は
観測能力の向上により、さらに強化される。
例えば、OSSOSによる継続的な観測に加え
OSSOSによる継続的な観測に加え、ベラ・C・ルービン観測所によって検出された天体のデータベースが飛躍的に拡大されるでしょうし、JWST
JWSTは、太陽系の惑星形成の初期段階を探る新たな方法を提供します。
また、JWSTは太陽系内の惑星形成の初期段階を探る新たな方法を提供します。さらに、新しい
ルーシーやプシュケのような新しいミッションが建設中であるか、すでに
さらに、ルーシーやプシュケのような新しいミッションが、太陽系外縁部の探査のために建設中か、すでにその途上にあるのです。
最後に、数値モデルの改善、新しい観測施設の稼動、そして新たな惑星候補の発見により、太陽系はますます発展していくことでしょう。
新しい観測施設が稼働し、新しいミッションが誕生しています。
私たちは今、太陽系外縁部の黄金時代に生きているのです。
惑星系彗星探査の黄金時代です。このように、私たちは小天体研究の未来は、実に明るい。という楽観的な見方があるはずです。