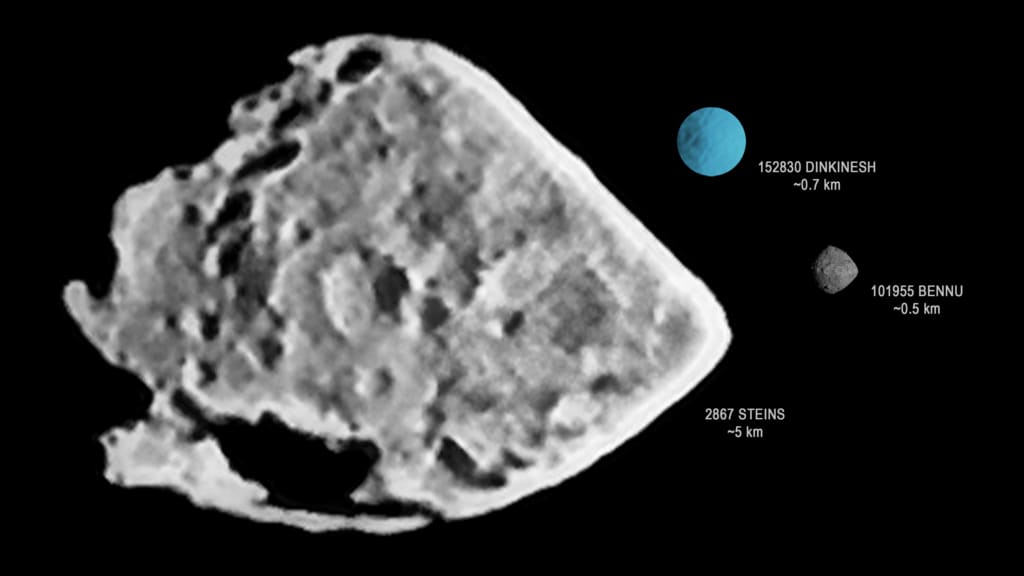
ルーシーミッションの探査目標ディンキネシュWISE観測で有効径760mアルベド0.27と出た。以下、機械翻訳。
WISE データを使用した (152830) ディンキネシュのサイズとアルベドの制約
概要
小さなメインベルト小惑星を探査すると、さまざまな過程を通じてその形成と進化についての洞察が得られます。
動的かつ衝突的なプロセス。 これらの小惑星は、潜在的に存在するものとサイズが重なっています。
地球近傍の危険な物体人口を調査し、これらの物体の大部分を供給します。 ルーシーのミッション
小さなメインベルト小惑星 (152830) ディンキネシュの研究の機会を提供します。 宇宙船
へのミッションの準備として、2023年11月1日にこの天体のフライバイを実行する予定です。
木星トロヤ群小惑星。 得られたディンキネシュの積層フレームに絞り測光を採用しました。
Wide-field-Infrared Survey Explorer によって測定され、12μm での検出に対して熱モデリングが実行されました。
直径とアルベド値を計算します。 この方法を通じて、ディンキネシュには効果的な効果があると判断しました。
球径0.76+0.11−0.21km、視覚的な幾何学的アルベドは 0.27+0.25−0.06
16回目は、84 パーセンタイル。 このアルベドは、典型的な石質 (S 型) 小惑星と一致します。
キーワード: WISE — NEOWISE — メインベルト小惑星 — IRSA
1。概要
私たちの太陽系は塵とガスの分子雲から形成され、太陽系星雲が平らになって円盤になり、
原始太陽が形成され、塵粒子が凝縮し始めた (Weidenschilling 1977)。 これらの粒子は最終的に微惑星を形成しました
降着による。 一部の微惑星は今日私たちが知っている惑星を形成しましたが、他の微惑星は成長が止まった可能性があります。
より小さいサイズ。 メインベルト小惑星の組成は、それらが原始惑星内のどこで形成されたかによって異なります。
円盤とそれらが初期の太陽系でどのように混合されたか (Morbidelli et al. 2009; DeMeo et al. 2015)。 混合してもよい
惑星の移動や流れの不安定性によって発生したものである(Carrera et al. 2015; Tsiganis et al.
2005)。 さらに、衝突カスケードにより小さな破片のシャワーが発生し、より迅速に移動する可能性があります。
非重力力(すなわち、Yarkovsky ドリフト; Bottke et al. 2005a,b; Gomes et al. 2005)。 これらの小さな断片
また、ベンヌ、リュウグウ、イトカワのような瓦礫の山に再付着する可能性もあります (e.g.、nakamura et al. 2023)。 小さなメインベルト
私たちが今日太陽系で観察している小惑星は、おそらくこれらのプロセスの組み合わせの結果であると考えられます(ボトケ)
他。 2015)。 小さなメインベルト小惑星を研究することで、その形成とその後の進化についての洞察を得ることができます。
メインベルトの小さな小惑星も、現在の地球近傍天体 (NEO) に栄養を与えているため、研究することが重要です。
人口の一部は地球に影響を与える可能性があり、その規模は地球規模と重なるため、
最大の NEO (Alvarez et al. 1980)。 しかし、観測効果により、メインベルトの小さな小惑星の研究は困難になっています。
なぜなら、それらはしばしば非常にかすかであったり、遠くにあったり、小さかったりするからです。 木星トロヤ群小惑星の探査に向かうNASAのルーシー
探査機は、2023年 11月 1日に小さなメインベルト小惑星 (152830) ディンキネシュの近くを飛行します。ルーシーのミッションは、
熱赤外分光計、高解像度パンクロマチックイメージャ、赤外イメージングを使用して観察を収集します。
分光計、およびカラーカメラ (Levison et al. 2021)。 これらの機器は小惑星の直径も提供します
解決された形状モデルとして。 Lucy は、視覚的な幾何学的アルベド、スピン状態、カラー マップ、および体積と密度の制約に関する情報も取得します。 ディンキネシュは、詳細なフライバイが可能な最小のメインベルト小惑星となる
データ。
ディンキネシュは、1999 年のリンカーン地球近傍小惑星計画 (LINEAR; Stokes et al. 2000) の調査によって発見されました。
十分に制約された軌道を提供するのに十分な量のマルチエポック観測があり、ディンキネシュを
適切な宇宙船フライバイターゲット。 ボーリンら。 (2023) は Keck を使用して分光観測を得ることができました。
ディンキネシュが S 型/Sq 型小惑星であり、アルベド範囲を使用していることを示したジェミニ南望遠鏡
Mainzerらから。 (2011a) および Mottola et al. による HV の絶対可視等級 = 17.62 ± 0.04 mag
(2023)、ボーリンら。 (2023) の関係に基づいて有効直径範囲 0.67 〜 0.96 km を計算
Deff = 1329p−1/2 V 10−HV /5 km (Fowler & Chillemi 1992)。 これらの結果は de Le'on らの結果とよく一致しています。
(2023)、HV = 17.48 ± 0.05 mag および 0.16 < GV < 0.23 mag を得て、有効球径を与えました。
範囲は 0.542 〜 1.309 km、Mottola et al. (2023) 誰が発見した G = 0.378 等の直径範囲を与える
2σで0.66 − 1.36 km。 モットラら。 (2023) ディンキネシュの光度曲線測光も取得し、回転角度を発見しました。
周期 P = 52.67 ± 0.04 時間、ゆっくりと回転する物体を示します。
この論文では、ディンキネシュのサイズと視覚的な幾何学的アルベドの独立した測定結果を報告します。
Wide-field Infrared Survey Explorer の 12μm スタック測光に基づく熱モデリングから導出
2010 年に撮影 (Wright et al. 2010; Mainzer et al. 2011b)。
2. 観察
Wide-field Infrared Survey Explorer (WISE; Wright et al. 2010) は、全天地図を作成した NASA のミッションです。
3.4、4.6、12、22 µm にわたる 4 つの波長 (それぞれ W1、W2、W3、W4 と表記)。 に発売されました
2009 年 12 月 14 日、その時点では 4 つのバンドすべてが利用可能でした。 WISEは完全極低温での主要任務を完了した
その主な科学的目的は小惑星を観察することではありませんでしたが、約 190,000 個の小惑星を検出することができました。
それらのうち、自動検出ソフトウェアを使用したもの (Mainzer et al. 2011b)。 全盛期が無事に完了した後、
ミッションの後、WISE 探査機は 2013 年末に再起動され、地球近傍物体広視野赤外線探査機に改名されました。
Survey Explorer (NEOWISE; Mainzer et al. 2014)。主な焦点は、
まだ動作していた 2 つの短波長チャネル、W1 と W2。 熱波長での観測により、
熱モデルを使用した小惑星の直径の決定、および熱モデルに加えて可視光データが利用可能かどうか
測定により、直径だけでなく可視アルベドも決定できます。
最初の完全極低温調査中に、WISE は位置をカバーする 19 の独立した暴露セットを取得しました。
ディンキネシュ産のもので、そのうち 17 個は良質でした。 表 1 は私たちの観察をまとめたものです。 小惑星は一般的に、
個々の露出では検出できないほど淡いですが、高品質のフレームを登録して追加しました
各露光時の小惑星の位置を測定し、シフトした画像を加算します。 露出
背景の星や銀河と一致する小惑星の予測位置も、事前に除外されました。
coadd、AllWISE ソース カタログ (Cutri 2014) の調査に基づいています。 月から 20°以内で撮影された露出
も除外されました。 残りの 17 枚の露出は、オプションの解像度を備えた画像加算を使用して結合されました。
Enhancement (ICORE; Masci & Fowler 2009; Masci 2013) アルゴリズム.1 4 つの WISE で生成された相互追加画像
帯域を図 1 に示します。物体は 12 µm で約 5 の信号対雑音比 (SNR) で検出されます。 探しました
NEOWISE W1 および W2 は完全極低温ミッション後に撮影されましたが、何も検出されませんでした。
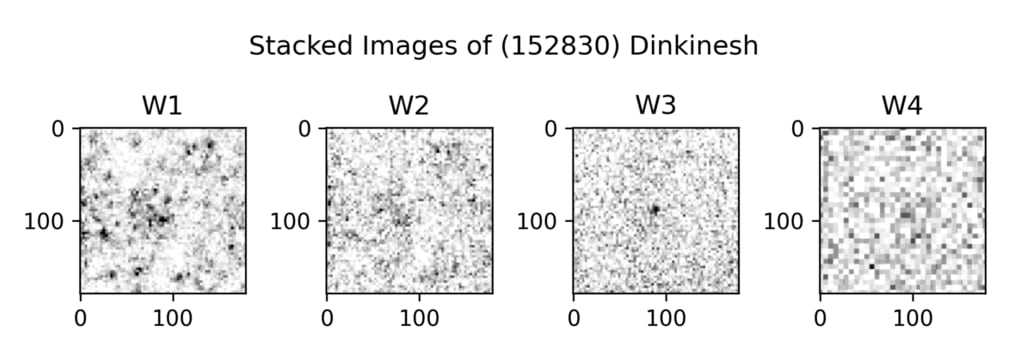
図 1. WISE バンド W1、W2、W3、および W4 におけるディンキネシュのスタック画像測光。
3. 方法
入れ子になった円形絞りのセットを使用して、ディンキネシュの同時追加画像に対して絞り測光を実行しました。
バンド W3 の半径は 11、12、14、18、22、26、33 秒角で、空のレベルを推定するための大きな環状領域があります。
信号。 W1 と W2 の画像は、星が汚れているため、測光を実行しませんでした。
銀河緯度が低い(ディンキネシュは観測時に銀河面から5°離れていた)。 物体は暗すぎて見えませんでした
これらのデータは、明るさの上限を設定するために使用できますが、スタックされた W4 フレームで顕著な検出が生成されます。
限界。
WISE のプロファイル フィット測光を使用して、絞り光源測光を確立された測光標準に合わせて校正しました。 280 個の明るく不飽和の小惑星 (SNR > 30.0 および W3 > 4.0) のスタックを作成しました。
マグニチュード) ICORE アルゴリズムを使用して。 次に、各オブジェクトの重ね合わせ画像の絞り測光を計算し、
それをそのオブジェクトのプロファイルフィット測光と比較しました。 無関係なソースにフラグを立てるアルゴリズムを採用しました
星、宇宙線、回折スパイク、光学アーチファクト、プロファイルフィット測光による不鮮明な画像など。
拒否基準には、dtanneal > 2000 秒、cc flags = 0、qi fat = 0、rchi2 < 5、および Moon sep > 20 が含まれていました。
。 どれでも
AllWISE による、フレーム内の小惑星の予測位置から 5 秒角以内、1 等級以内の検出
小惑星の信号は除外されました。 280 個のオブジェクトのそれぞれについて、プロファイル フィット間のオフセットを計算しました。
W3 等級と 7 つの積み重ねられた絞り等級すべて。 次に、各オフセットの平均を計算しました。
図 2 に示すように、成長曲線を得るために開口サイズを調整しました。私たちは、バックグラウンド ノイズを最小限に抑えるよう努めました。
また、量子化効果を誘発する過度に小さい開口サイズも避けます。 絞り値 3 を選択しました。
半径 14 秒角が最適なバランスです。 測光校正の不確かさの限界は、WISE (Cutri) の場合 0.03 等級です。
他。 2012).2 補正項を減らすのに十分な明るい小惑星を使用して、絞り補正を導き出しました。
不確実性 (0.23 ± 0.05 等、図 2) はディンキネシュの測光測定の不確かさよりもはるかに小さく、
〜±0.2等でした。 絞り補正項をディンキネシュの絞りの大きさに適用して、補正を戻しました。
校正されたプロファイルに W3 の大きさを当てはめます (表 1)。 絞り 2 と 3 (それぞれ 12 秒角と 14 秒角) をテストしました。
そして統計的不確実性の範囲内では結果は同じでした。
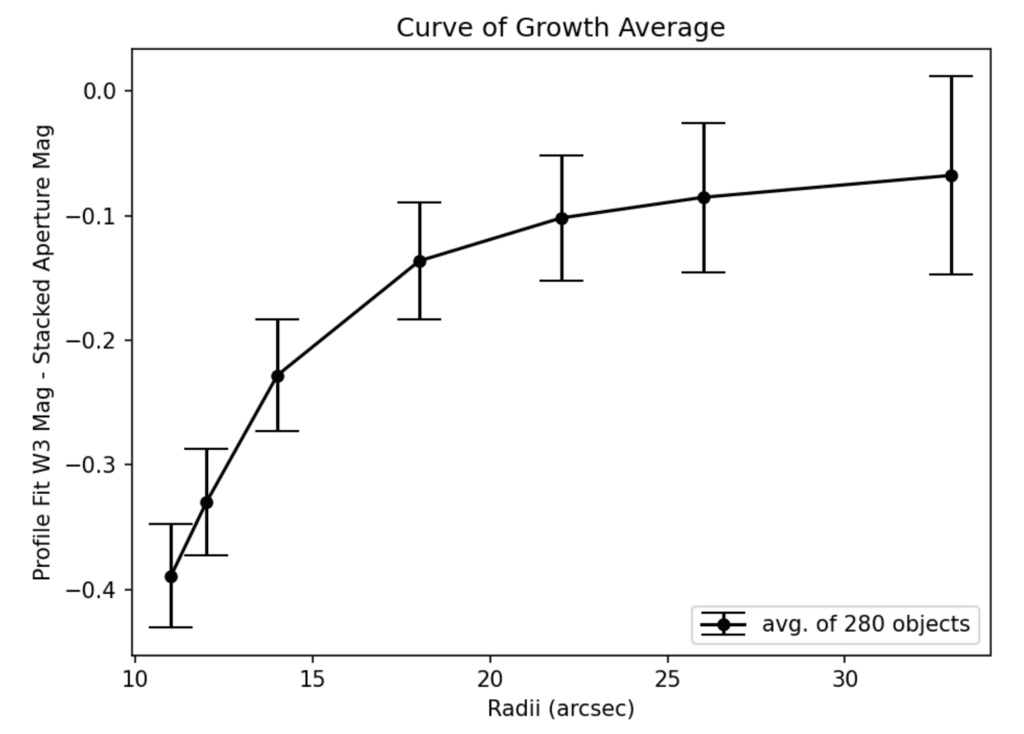
図 2. 280 個の明るい不飽和天体の平均プロファイル フィット マグニチュードから積み重ねられた開口部を差し引いた値を計算しました。
被写体ごとに測光します。 次に、280 個のオブジェクトのオフセットを平均して、バンド W3 の増加曲線を計算しました。 オフセット
絞り 2 のオフセットは -0.33 等、絞り 3 のオフセットは -0.23 等でした。
3.1. 熱モデリング
地球近傍小惑星熱モデル (NEATM) は、以前のバージョンを改良した単純な熱モデルです。
標準熱モデルや高速回転モデルなど (Harris 1998)。 標準的な熱モデルは、日射量と表面温度が瞬間的に変化する間、小惑星を非回転の球体として近似します。
平衡(Lebofsky et al. 1986)。 高速回転モデル (Lebofsky & Spencer 1989) は、温度が
は、小惑星の周囲の緯度に均一な帯状に分布しています。 以前の研究のため、私たちの研究では NEATM を使用しています。
(Mainzer et al. 2011a; Wright et al. 2018; Masiero et al. 2021) は、直径測定値が
NEATM を使用して NEOWISE から決定された値は、一般に 10% 以内の信頼性があり、計算効率が高いです。
NEATM は、小惑星の表面全体の温度分布をモデル化するために多くの仮定を立てます。 の
NEATM モデルは、小惑星が回転しておらず、夜側の温度が 0 K であると仮定しています。
NEATM の実装では、十分な数の三角形のファセットを配置して球を近似します。
フィボナッチ格子 3 このモデルには、複数の熱的に支配的なバンドが存在する場合に、熱慣性や表面粗さなどの追加の熱パラメータを考慮して変更できるビーム パラメータ η も組み込まれています。
ご利用いただけます。 Python ベイシンホッパーを使用して最適なソリューションを見つけます (Wales & Doye 1997; Virtanen et al. 2020)
パッケージ化して、Python 司会者によって実装されたモンテカルロ マルコフ連鎖アプローチを使用して不確実性を見つけます
パッケージ (Foreman-Mackey 他、2013)。
ディンキネシュに NEATM を適用して、その有効球径とアルベド値を取得します。 放射率を設定します
隕石の研究に基づいて値を 0.9 にしました (Bates et al. 2021; Ostrowski & Bryson 2020)。 HV=17.62±0.04を採用
mag は、Mottola らの測光測定に基づいています。 (2023年)。 同様に、G = 0.378 mag を採用しました。
モットラら。 (2023) しかし、0.08 から 0.38 等の全範囲にわたって G をテストしたところ、統計的には十分ではないことがわかりました。
直径は G にほとんど依存しないため、結果に大きな違いが生じます。
熱的に支配的な複数のバンドでの測定では、以下に基づいてビーム値 η を 1.00 ±0.1 と仮定しました。
マシエロら。 (2011年、2014年)。
4. 結果/考察
ディンキネシュの自転周期は 52.67 時間だったのに対し、私たちは 36.5 時間かけて観察しました (Mottola et al.
2023年)。 WISE による長時間の観測により、有効球径をより適切に制限することができます。
その全回転サイクルのほとんどを観察することによって。 熱モデルを通じて、ディンキネシュには次のような特徴があることが判明しました。
有効球径0.76+0.11−0.21 km、視覚的な幾何学的アルベドは 0.27+0.25 -0.06
不確実性を指定すると16 パーセンタイルと 84 パーセンタイルで。 図 3 は、熱モデルからの最適解を示しています。 アルベドは一貫しています
S 型小惑星の典型的な値の範囲と一致します (Mainzer et al. 2011c)。
また、Wright (2007) および Koren et al. に記載されている球面熱物理モデル (TPM) も使用しました。 (2015)から
ディンキネシュの直径を決定します。これより小さい推定値は 621+92−117メートル です。
。 ほとんどの直径が異なります
TPM と NEATM の間のずれは、ディンキネシュの異常に長い自転周期 (P = 52.67 時間) によって引き起こされます。
直径は 700 m 近くの典型的な天体の中央値よりも 1 桁長いです。 これはそれよりも小さいです
NEATM フィット サイズですが、不確実性の範囲内で一貫しています。 利用可能なデータが限られているため、NEATM を推奨します。
4.1. 潜在的な小惑星家族協会
小惑星ファミリーの関連付けは、軌道歳差運動速度や固有軌道要素を比較することによって行うことができます (平山)
1918年。 ミラニ&クネゼヴィッチ 1994年。 クネゼヴィッチら。 2002年)。 小惑星 (152830) ディンキネシュは正式には小惑星の一部ではありません
ただし、ディンキネシュの合成固有軌道要素 (Kneˇzevi´c & Milani 2003) は非常に近い値を示しています。
小惑星のものと一致します (8) 適切な長半径 (2.191 vs 2.201 天文単位)、適切な離心率 (0.1482 vs
0.1449)、近日点歳差運動の速度 g (32.810 vs 32.017 arcsec/年)、および昇交節歳差運動の速度 s (-35.502)
対 -35.511 秒角/年)、適切な傾斜でのみ逸脱します(1.600 対 5.574 °)。
これは、ディンキネシュとフローラ家の間に潜在的なつながりがあることを示唆しており、
傾斜は、家族形成の影響による初速度の結果、または季節的なヤルコフスキーによるものです。
傾斜角を持つオブジェクトに対して大きな面外成分を持つ効果 (Vokrouhlick´y & Farinella 1999)
軌道面に対して平行でも直交でもない(Bottke et al. 2002)。 このリンクはさらにサポートされています。
ディンキネシュとフローラのスペクトル分類間の一貫性。
5。結論
我々は、2010 年 3 月に WISE によって取得された複数の独立した露光を加算することにより、小さなメインベルト小惑星 (152830) ディンキネシュの 12 μm での測光を取得しました。我々は 2 つの熱モデル、NEATM と TPM を使用して、
直径と視覚的な幾何学的値。 これらの値は、予測された直径およびアルベドとよく一致しています。
Bolinらの範囲です。 (2023); デ・レオンら。 (2023)、Mottola et al. (2023年)。 a/bの軸比より 〜1.43
(Mottola et al. 2023) による光度曲線の振幅から導出された、球相当サイズ 0.76+0.11−0.21km
私たちの測定が完全にサンプリングされていると仮定すると、軸サイズ 2a = 0.96 km および 2b = 2c = 0.67 km に相当します。
ディンキネシュの半回転。 WISE データから、視覚的な幾何学的アルベドは 0.27+0.25 −0.06であることが判明しました。
つまり典型的な S 型小惑星と一致します。 ルーシーのディンキネシュ飛行から得られるデータは、私たちに提供します。
非常に小さなメインベルト小惑星を詳細に観察します。 そうすることで、来歴をより深く理解できるようになります。
そのようなオブジェクトの。
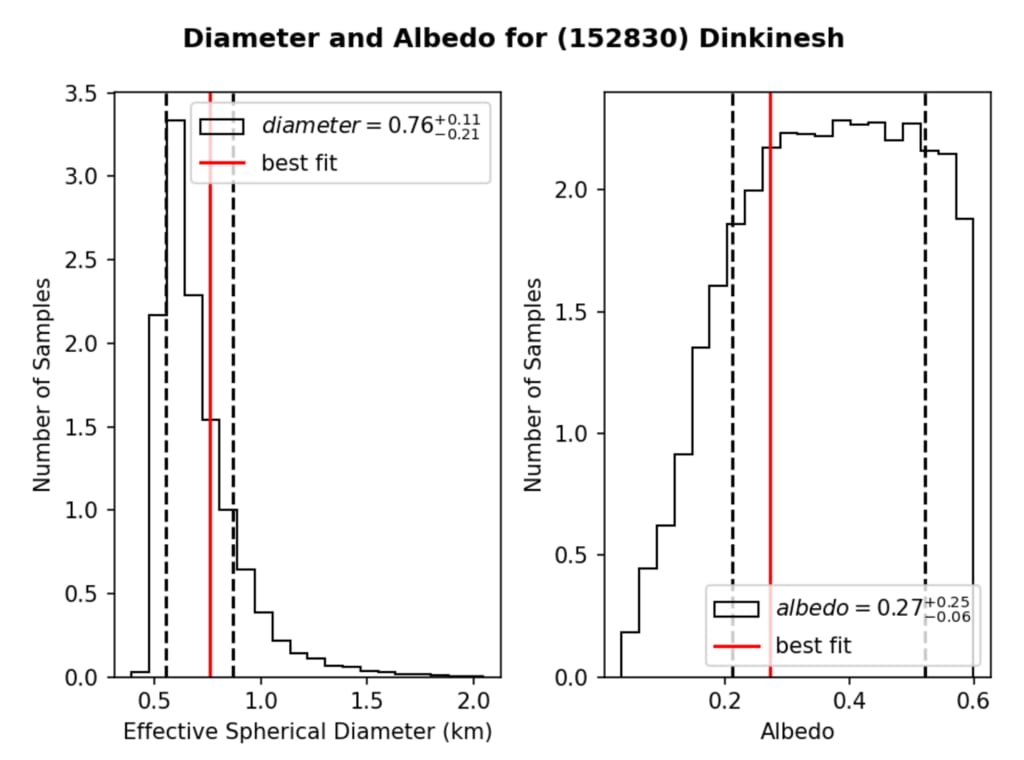
図 3. ディンキネシュの有効球径 (左) と視覚的な幾何学的アルベド (右) を決定しました。 の
ヒストグラムは、モンテカルロ マルコフ連鎖試行からの確率分布関数を表します。 赤い線が表すのは、
両方のパラメーターの確率分布を調査するためのモンテカルロ マルコフ連鎖試行からの最良の適合。 二つ
破線は 16 パーセンタイルと 84 パーセンタイルを表します。
WISE データを使用した (152830) ディンキネシュのサイズとアルベドの制約
概要
小さなメインベルト小惑星を探査すると、さまざまな過程を通じてその形成と進化についての洞察が得られます。
動的かつ衝突的なプロセス。 これらの小惑星は、潜在的に存在するものとサイズが重なっています。
地球近傍の危険な物体人口を調査し、これらの物体の大部分を供給します。 ルーシーのミッション
小さなメインベルト小惑星 (152830) ディンキネシュの研究の機会を提供します。 宇宙船
へのミッションの準備として、2023年11月1日にこの天体のフライバイを実行する予定です。
木星トロヤ群小惑星。 得られたディンキネシュの積層フレームに絞り測光を採用しました。
Wide-field-Infrared Survey Explorer によって測定され、12μm での検出に対して熱モデリングが実行されました。
直径とアルベド値を計算します。 この方法を通じて、ディンキネシュには効果的な効果があると判断しました。
球径0.76+0.11−0.21km、視覚的な幾何学的アルベドは 0.27+0.25−0.06
16回目は、84 パーセンタイル。 このアルベドは、典型的な石質 (S 型) 小惑星と一致します。
キーワード: WISE — NEOWISE — メインベルト小惑星 — IRSA
1。概要
私たちの太陽系は塵とガスの分子雲から形成され、太陽系星雲が平らになって円盤になり、
原始太陽が形成され、塵粒子が凝縮し始めた (Weidenschilling 1977)。 これらの粒子は最終的に微惑星を形成しました
降着による。 一部の微惑星は今日私たちが知っている惑星を形成しましたが、他の微惑星は成長が止まった可能性があります。
より小さいサイズ。 メインベルト小惑星の組成は、それらが原始惑星内のどこで形成されたかによって異なります。
円盤とそれらが初期の太陽系でどのように混合されたか (Morbidelli et al. 2009; DeMeo et al. 2015)。 混合してもよい
惑星の移動や流れの不安定性によって発生したものである(Carrera et al. 2015; Tsiganis et al.
2005)。 さらに、衝突カスケードにより小さな破片のシャワーが発生し、より迅速に移動する可能性があります。
非重力力(すなわち、Yarkovsky ドリフト; Bottke et al. 2005a,b; Gomes et al. 2005)。 これらの小さな断片
また、ベンヌ、リュウグウ、イトカワのような瓦礫の山に再付着する可能性もあります (e.g.、nakamura et al. 2023)。 小さなメインベルト
私たちが今日太陽系で観察している小惑星は、おそらくこれらのプロセスの組み合わせの結果であると考えられます(ボトケ)
他。 2015)。 小さなメインベルト小惑星を研究することで、その形成とその後の進化についての洞察を得ることができます。
メインベルトの小さな小惑星も、現在の地球近傍天体 (NEO) に栄養を与えているため、研究することが重要です。
人口の一部は地球に影響を与える可能性があり、その規模は地球規模と重なるため、
最大の NEO (Alvarez et al. 1980)。 しかし、観測効果により、メインベルトの小さな小惑星の研究は困難になっています。
なぜなら、それらはしばしば非常にかすかであったり、遠くにあったり、小さかったりするからです。 木星トロヤ群小惑星の探査に向かうNASAのルーシー
探査機は、2023年 11月 1日に小さなメインベルト小惑星 (152830) ディンキネシュの近くを飛行します。ルーシーのミッションは、
熱赤外分光計、高解像度パンクロマチックイメージャ、赤外イメージングを使用して観察を収集します。
分光計、およびカラーカメラ (Levison et al. 2021)。 これらの機器は小惑星の直径も提供します
解決された形状モデルとして。 Lucy は、視覚的な幾何学的アルベド、スピン状態、カラー マップ、および体積と密度の制約に関する情報も取得します。 ディンキネシュは、詳細なフライバイが可能な最小のメインベルト小惑星となる
データ。
ディンキネシュは、1999 年のリンカーン地球近傍小惑星計画 (LINEAR; Stokes et al. 2000) の調査によって発見されました。
十分に制約された軌道を提供するのに十分な量のマルチエポック観測があり、ディンキネシュを
適切な宇宙船フライバイターゲット。 ボーリンら。 (2023) は Keck を使用して分光観測を得ることができました。
ディンキネシュが S 型/Sq 型小惑星であり、アルベド範囲を使用していることを示したジェミニ南望遠鏡
Mainzerらから。 (2011a) および Mottola et al. による HV の絶対可視等級 = 17.62 ± 0.04 mag
(2023)、ボーリンら。 (2023) の関係に基づいて有効直径範囲 0.67 〜 0.96 km を計算
Deff = 1329p−1/2 V 10−HV /5 km (Fowler & Chillemi 1992)。 これらの結果は de Le'on らの結果とよく一致しています。
(2023)、HV = 17.48 ± 0.05 mag および 0.16 < GV < 0.23 mag を得て、有効球径を与えました。
範囲は 0.542 〜 1.309 km、Mottola et al. (2023) 誰が発見した G = 0.378 等の直径範囲を与える
2σで0.66 − 1.36 km。 モットラら。 (2023) ディンキネシュの光度曲線測光も取得し、回転角度を発見しました。
周期 P = 52.67 ± 0.04 時間、ゆっくりと回転する物体を示します。
この論文では、ディンキネシュのサイズと視覚的な幾何学的アルベドの独立した測定結果を報告します。
Wide-field Infrared Survey Explorer の 12μm スタック測光に基づく熱モデリングから導出
2010 年に撮影 (Wright et al. 2010; Mainzer et al. 2011b)。
2. 観察
Wide-field Infrared Survey Explorer (WISE; Wright et al. 2010) は、全天地図を作成した NASA のミッションです。
3.4、4.6、12、22 µm にわたる 4 つの波長 (それぞれ W1、W2、W3、W4 と表記)。 に発売されました
2009 年 12 月 14 日、その時点では 4 つのバンドすべてが利用可能でした。 WISEは完全極低温での主要任務を完了した
その主な科学的目的は小惑星を観察することではありませんでしたが、約 190,000 個の小惑星を検出することができました。
それらのうち、自動検出ソフトウェアを使用したもの (Mainzer et al. 2011b)。 全盛期が無事に完了した後、
ミッションの後、WISE 探査機は 2013 年末に再起動され、地球近傍物体広視野赤外線探査機に改名されました。
Survey Explorer (NEOWISE; Mainzer et al. 2014)。主な焦点は、
まだ動作していた 2 つの短波長チャネル、W1 と W2。 熱波長での観測により、
熱モデルを使用した小惑星の直径の決定、および熱モデルに加えて可視光データが利用可能かどうか
測定により、直径だけでなく可視アルベドも決定できます。
最初の完全極低温調査中に、WISE は位置をカバーする 19 の独立した暴露セットを取得しました。
ディンキネシュ産のもので、そのうち 17 個は良質でした。 表 1 は私たちの観察をまとめたものです。 小惑星は一般的に、
個々の露出では検出できないほど淡いですが、高品質のフレームを登録して追加しました
各露光時の小惑星の位置を測定し、シフトした画像を加算します。 露出
背景の星や銀河と一致する小惑星の予測位置も、事前に除外されました。
coadd、AllWISE ソース カタログ (Cutri 2014) の調査に基づいています。 月から 20°以内で撮影された露出
も除外されました。 残りの 17 枚の露出は、オプションの解像度を備えた画像加算を使用して結合されました。
Enhancement (ICORE; Masci & Fowler 2009; Masci 2013) アルゴリズム.1 4 つの WISE で生成された相互追加画像
帯域を図 1 に示します。物体は 12 µm で約 5 の信号対雑音比 (SNR) で検出されます。 探しました
NEOWISE W1 および W2 は完全極低温ミッション後に撮影されましたが、何も検出されませんでした。

図 1. WISE バンド W1、W2、W3、および W4 におけるディンキネシュのスタック画像測光。
3. 方法
入れ子になった円形絞りのセットを使用して、ディンキネシュの同時追加画像に対して絞り測光を実行しました。
バンド W3 の半径は 11、12、14、18、22、26、33 秒角で、空のレベルを推定するための大きな環状領域があります。
信号。 W1 と W2 の画像は、星が汚れているため、測光を実行しませんでした。
銀河緯度が低い(ディンキネシュは観測時に銀河面から5°離れていた)。 物体は暗すぎて見えませんでした
これらのデータは、明るさの上限を設定するために使用できますが、スタックされた W4 フレームで顕著な検出が生成されます。
限界。
WISE のプロファイル フィット測光を使用して、絞り光源測光を確立された測光標準に合わせて校正しました。 280 個の明るく不飽和の小惑星 (SNR > 30.0 および W3 > 4.0) のスタックを作成しました。
マグニチュード) ICORE アルゴリズムを使用して。 次に、各オブジェクトの重ね合わせ画像の絞り測光を計算し、
それをそのオブジェクトのプロファイルフィット測光と比較しました。 無関係なソースにフラグを立てるアルゴリズムを採用しました
星、宇宙線、回折スパイク、光学アーチファクト、プロファイルフィット測光による不鮮明な画像など。
拒否基準には、dtanneal > 2000 秒、cc flags = 0、qi fat = 0、rchi2 < 5、および Moon sep > 20 が含まれていました。
。 どれでも
AllWISE による、フレーム内の小惑星の予測位置から 5 秒角以内、1 等級以内の検出
小惑星の信号は除外されました。 280 個のオブジェクトのそれぞれについて、プロファイル フィット間のオフセットを計算しました。
W3 等級と 7 つの積み重ねられた絞り等級すべて。 次に、各オフセットの平均を計算しました。
図 2 に示すように、成長曲線を得るために開口サイズを調整しました。私たちは、バックグラウンド ノイズを最小限に抑えるよう努めました。
また、量子化効果を誘発する過度に小さい開口サイズも避けます。 絞り値 3 を選択しました。
半径 14 秒角が最適なバランスです。 測光校正の不確かさの限界は、WISE (Cutri) の場合 0.03 等級です。
他。 2012).2 補正項を減らすのに十分な明るい小惑星を使用して、絞り補正を導き出しました。
不確実性 (0.23 ± 0.05 等、図 2) はディンキネシュの測光測定の不確かさよりもはるかに小さく、
〜±0.2等でした。 絞り補正項をディンキネシュの絞りの大きさに適用して、補正を戻しました。
校正されたプロファイルに W3 の大きさを当てはめます (表 1)。 絞り 2 と 3 (それぞれ 12 秒角と 14 秒角) をテストしました。
そして統計的不確実性の範囲内では結果は同じでした。

図 2. 280 個の明るい不飽和天体の平均プロファイル フィット マグニチュードから積み重ねられた開口部を差し引いた値を計算しました。
被写体ごとに測光します。 次に、280 個のオブジェクトのオフセットを平均して、バンド W3 の増加曲線を計算しました。 オフセット
絞り 2 のオフセットは -0.33 等、絞り 3 のオフセットは -0.23 等でした。
3.1. 熱モデリング
地球近傍小惑星熱モデル (NEATM) は、以前のバージョンを改良した単純な熱モデルです。
標準熱モデルや高速回転モデルなど (Harris 1998)。 標準的な熱モデルは、日射量と表面温度が瞬間的に変化する間、小惑星を非回転の球体として近似します。
平衡(Lebofsky et al. 1986)。 高速回転モデル (Lebofsky & Spencer 1989) は、温度が
は、小惑星の周囲の緯度に均一な帯状に分布しています。 以前の研究のため、私たちの研究では NEATM を使用しています。
(Mainzer et al. 2011a; Wright et al. 2018; Masiero et al. 2021) は、直径測定値が
NEATM を使用して NEOWISE から決定された値は、一般に 10% 以内の信頼性があり、計算効率が高いです。
NEATM は、小惑星の表面全体の温度分布をモデル化するために多くの仮定を立てます。 の
NEATM モデルは、小惑星が回転しておらず、夜側の温度が 0 K であると仮定しています。
NEATM の実装では、十分な数の三角形のファセットを配置して球を近似します。
フィボナッチ格子 3 このモデルには、複数の熱的に支配的なバンドが存在する場合に、熱慣性や表面粗さなどの追加の熱パラメータを考慮して変更できるビーム パラメータ η も組み込まれています。
ご利用いただけます。 Python ベイシンホッパーを使用して最適なソリューションを見つけます (Wales & Doye 1997; Virtanen et al. 2020)
パッケージ化して、Python 司会者によって実装されたモンテカルロ マルコフ連鎖アプローチを使用して不確実性を見つけます
パッケージ (Foreman-Mackey 他、2013)。
ディンキネシュに NEATM を適用して、その有効球径とアルベド値を取得します。 放射率を設定します
隕石の研究に基づいて値を 0.9 にしました (Bates et al. 2021; Ostrowski & Bryson 2020)。 HV=17.62±0.04を採用
mag は、Mottola らの測光測定に基づいています。 (2023年)。 同様に、G = 0.378 mag を採用しました。
モットラら。 (2023) しかし、0.08 から 0.38 等の全範囲にわたって G をテストしたところ、統計的には十分ではないことがわかりました。
直径は G にほとんど依存しないため、結果に大きな違いが生じます。
熱的に支配的な複数のバンドでの測定では、以下に基づいてビーム値 η を 1.00 ±0.1 と仮定しました。
マシエロら。 (2011年、2014年)。
4. 結果/考察
ディンキネシュの自転周期は 52.67 時間だったのに対し、私たちは 36.5 時間かけて観察しました (Mottola et al.
2023年)。 WISE による長時間の観測により、有効球径をより適切に制限することができます。
その全回転サイクルのほとんどを観察することによって。 熱モデルを通じて、ディンキネシュには次のような特徴があることが判明しました。
有効球径0.76+0.11−0.21 km、視覚的な幾何学的アルベドは 0.27+0.25 -0.06
不確実性を指定すると16 パーセンタイルと 84 パーセンタイルで。 図 3 は、熱モデルからの最適解を示しています。 アルベドは一貫しています
S 型小惑星の典型的な値の範囲と一致します (Mainzer et al. 2011c)。
また、Wright (2007) および Koren et al. に記載されている球面熱物理モデル (TPM) も使用しました。 (2015)から
ディンキネシュの直径を決定します。これより小さい推定値は 621+92−117メートル です。
。 ほとんどの直径が異なります
TPM と NEATM の間のずれは、ディンキネシュの異常に長い自転周期 (P = 52.67 時間) によって引き起こされます。
直径は 700 m 近くの典型的な天体の中央値よりも 1 桁長いです。 これはそれよりも小さいです
NEATM フィット サイズですが、不確実性の範囲内で一貫しています。 利用可能なデータが限られているため、NEATM を推奨します。
4.1. 潜在的な小惑星家族協会
小惑星ファミリーの関連付けは、軌道歳差運動速度や固有軌道要素を比較することによって行うことができます (平山)
1918年。 ミラニ&クネゼヴィッチ 1994年。 クネゼヴィッチら。 2002年)。 小惑星 (152830) ディンキネシュは正式には小惑星の一部ではありません
ただし、ディンキネシュの合成固有軌道要素 (Kneˇzevi´c & Milani 2003) は非常に近い値を示しています。
小惑星のものと一致します (8) 適切な長半径 (2.191 vs 2.201 天文単位)、適切な離心率 (0.1482 vs
0.1449)、近日点歳差運動の速度 g (32.810 vs 32.017 arcsec/年)、および昇交節歳差運動の速度 s (-35.502)
対 -35.511 秒角/年)、適切な傾斜でのみ逸脱します(1.600 対 5.574 °)。
これは、ディンキネシュとフローラ家の間に潜在的なつながりがあることを示唆しており、
傾斜は、家族形成の影響による初速度の結果、または季節的なヤルコフスキーによるものです。
傾斜角を持つオブジェクトに対して大きな面外成分を持つ効果 (Vokrouhlick´y & Farinella 1999)
軌道面に対して平行でも直交でもない(Bottke et al. 2002)。 このリンクはさらにサポートされています。
ディンキネシュとフローラのスペクトル分類間の一貫性。
5。結論
我々は、2010 年 3 月に WISE によって取得された複数の独立した露光を加算することにより、小さなメインベルト小惑星 (152830) ディンキネシュの 12 μm での測光を取得しました。我々は 2 つの熱モデル、NEATM と TPM を使用して、
直径と視覚的な幾何学的値。 これらの値は、予測された直径およびアルベドとよく一致しています。
Bolinらの範囲です。 (2023); デ・レオンら。 (2023)、Mottola et al. (2023年)。 a/bの軸比より 〜1.43
(Mottola et al. 2023) による光度曲線の振幅から導出された、球相当サイズ 0.76+0.11−0.21km
私たちの測定が完全にサンプリングされていると仮定すると、軸サイズ 2a = 0.96 km および 2b = 2c = 0.67 km に相当します。
ディンキネシュの半回転。 WISE データから、視覚的な幾何学的アルベドは 0.27+0.25 −0.06であることが判明しました。
つまり典型的な S 型小惑星と一致します。 ルーシーのディンキネシュ飛行から得られるデータは、私たちに提供します。
非常に小さなメインベルト小惑星を詳細に観察します。 そうすることで、来歴をより深く理解できるようになります。
そのようなオブジェクトの。

図 3. ディンキネシュの有効球径 (左) と視覚的な幾何学的アルベド (右) を決定しました。 の
ヒストグラムは、モンテカルロ マルコフ連鎖試行からの確率分布関数を表します。 赤い線が表すのは、
両方のパラメーターの確率分布を調査するためのモンテカルロ マルコフ連鎖試行からの最良の適合。 二つ
破線は 16 パーセンタイルと 84 パーセンタイルを表します。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます