地球の自転エネルギーが月の公転に移動するだけでなく海水の移動で消費される。海流の駆動力として使われる。以下、機械翻訳。
地球と月の距離の共鳴潮汐進化
概要
地球と月のシステムでの潮汐相互作用により、地球のスピンが遅くなり、月が漂流します。この不況
現在、月は非常に正確に測定されていますが、50年以上前に、単純な潮汐モデルが外挿されていることがわかりました。
過去にさかのぼると、地質年代学的および地球化学的証拠とははるかに相容れない月の時代につながります。順番に
この問題を回避するために、海洋の潮汐散逸を考慮に入れて、より精巧なモデルが提案されています。しかし、これらは
モデルは、推定月齢と現在の月の後退の両方に同時に適合しませんでした。ここでは、物理的なものを提示します
これらの2つの制約を調整し、潮汐履歴の一意のソリューションを生成するモデル。このソリューションは、利用可能なものによく適合します
地球-月系の歴史のための地質学的プロキシと周期層序学の方法を統合します。結果として生じる進化
海洋散逸における共鳴の複数の交差を含み、これは、
月周回軌道距離、地球の1日の長さ、および地球の傾斜角。
キーワード。地球–月–惑星と衛星:動的進化と安定性–惑星と衛星:海
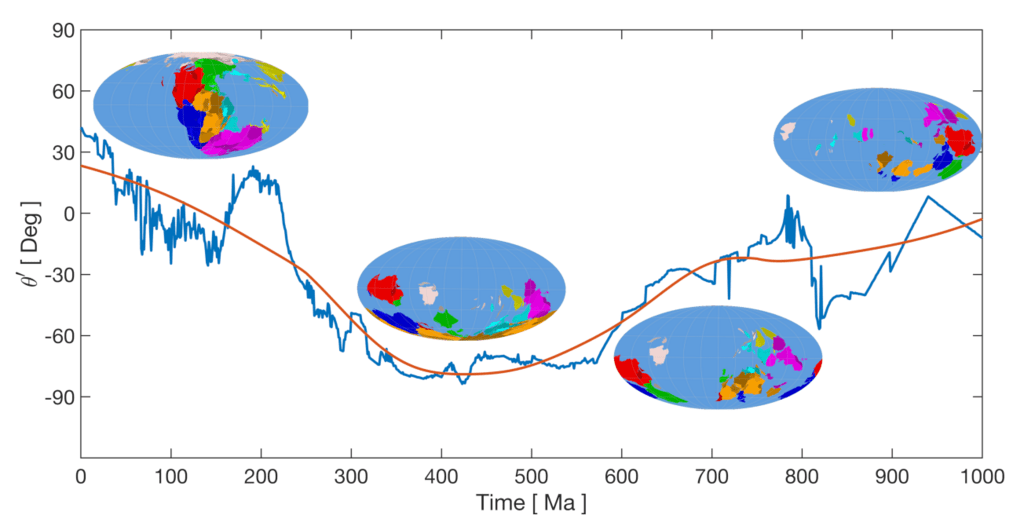
図1.過去10億年にわたる地表「古重心」の緯度の時間的進化プレートテクトニクス再構築は、Merdith et al。(2021)から採用され、
複数にわたる最初の運動学的に連続的な構造運動モデル
超大陸サイクル。 展開は、200Myrのウィンドウで移動多項式回帰フィルターを使用して赤で平滑化されます。 私たちの有効なモデルでは、この曲線は、半球形の大陸キャップの中心の進化をマッピングします。
中生代では赤道、古生代ではほぼ極性になります。
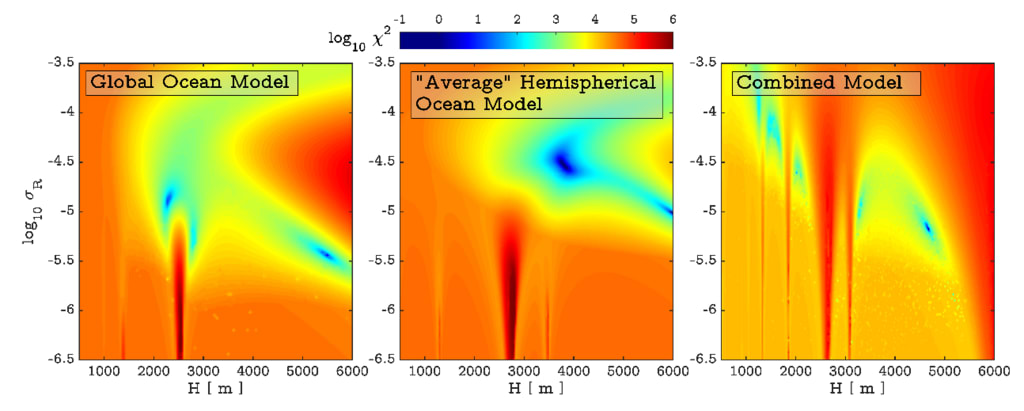
図2.χ^2の不適合面
研究された3つの幾何学的モデルについて。 地球と月のシステムの過去の動的進化は、
2つのフリーモデルパラメータHとσRの表示範囲。 不適合は、現在測定されている月の景気後退率を使用して確立されます。
LLR、および月齢(付録C)。 3つのモデルは、地史上、海洋シェルの形状が異なります。
他の2つよりも物理的なリアリズムを備えた複合モデル。 この分析の数値結果は(表C.1)に要約されています。 The
不適合の最小値のそれぞれに関連する動的進化は、図3の月の準主軸の観点からプロットされています。
図5、および図6の傾斜角と歳差運動の頻度。
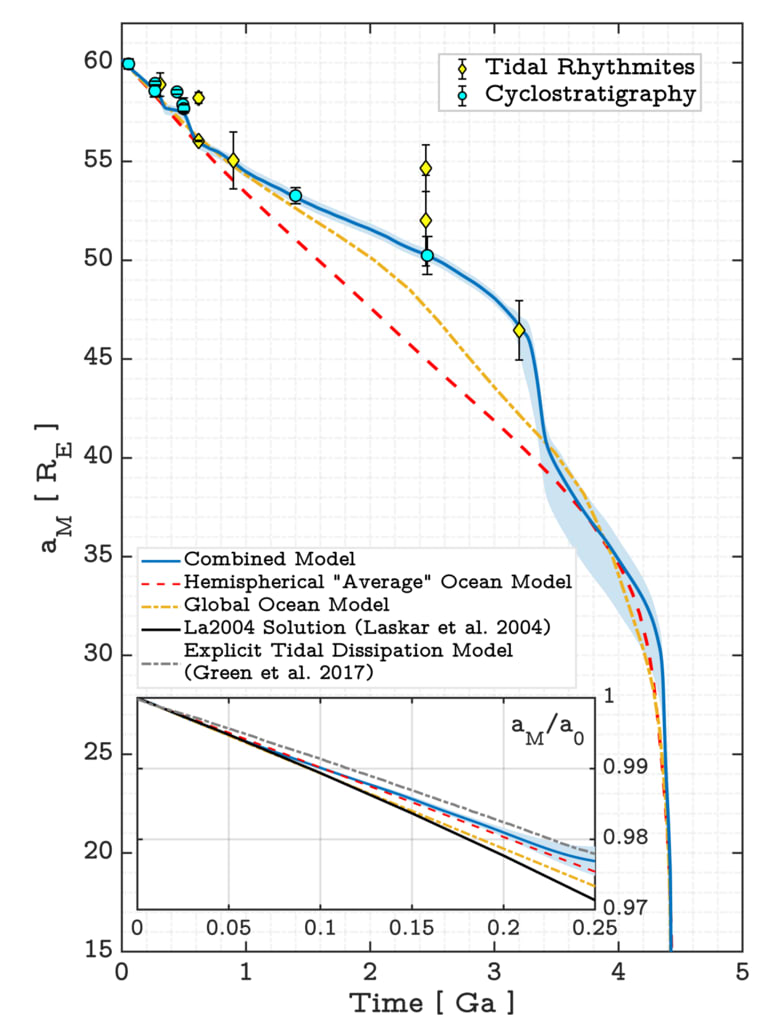
図3.月の準主軸の経時変化。 地球の月の分離aMは、
図2で説明されているように、自由パラメーター(H、σR)の最適値
と本文で。 進化曲線の上にプロットされているのは、周期層序学と潮汐層データからのaMの地質学的推論です(表D.1とD.2)。 影付きのエンベロープは2σ-不確かさに対応します
結合されたモデルの適合パラメータ(付録C)。 の中に
狭いウィンドウで、進化の最新の250 Myrsをズームし、古地理的再構成を使用した明示的な数値潮汐モデリングに対応する進化と比較します(Greenetal。
2017)、および数値解法La2004(Laskar
etal。 2004)。
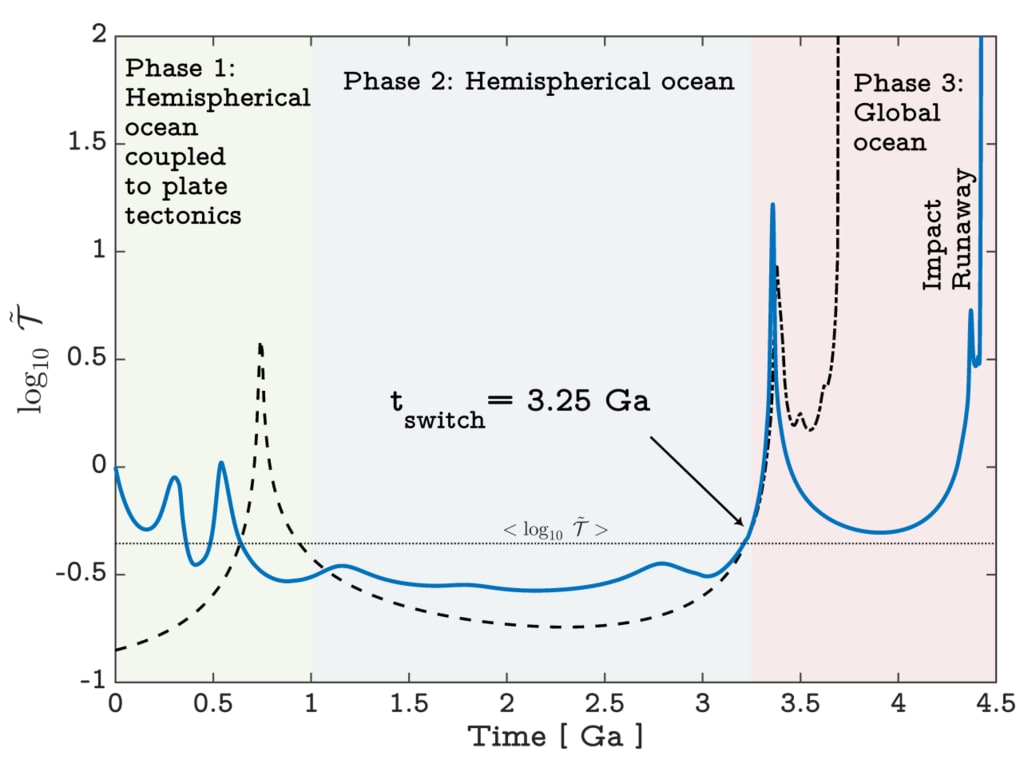
図4.潮汐トルクの履歴。半日周の対数
地球の潮汐トルク(現在の値で正規化:T〜 = T / T(t =
0))は時間の関数としてプロットされます。実線の曲線は
3つのフェーズを含む結合モデルのトルク:最初の
フェーズでは、半球形の海洋が地球の表面を移動し、図1の大陸の重心が進化します。
1 Gaを超える連続プレートテクトニクスモデル。フェーズ2では、
不連続性のモデリングを回避するために、半球形の海洋を1Gaの構成にします。これを超える減衰された潮汐トルクは注目に値します
位相は、固定された海洋位置によるものではなく、スペクトルの非共鳴バックグラウンドを占める潮汐応答によるものです。
この間隔に関連する潮汐周波数。 tswitchを超えて、
グローバル海洋構成のモデルのフェーズ3。破線と
一点鎖線の曲線は、指定された間隔で無視されるグローバルおよび半球形の海洋トルクにそれぞれ対応します
選択的結合モデルによる。
5.地質学研究の新しいターゲット
この記事では、最初の半解析的物理モデルを構築しました
これは、地球と月の進化における最も正確な制約、つまり現在の潮汐散逸率と月の年齢に適合します。
モデルを利用可能な地質データのいずれかに適合させることは意図的に避けています。驚くべき方法で、のユニークなソリューション
私たちの組み合わせたモデルは、大規模なセットにほぼ完全に一致します
それらの地質データ(図3および図5、6)。このソリューションは
地質学研究の新しいターゲットを提供します。それは明確に検証します
層序シーケンスから地球の歳差運動頻度を推定する周期層序アプローチ(Meyers&Malinverno 2018; Huangetal。2020;Sørensenetal。2020;Lantink
etal。 2021)(表D.1)。特に、周期層序学的評価
ジョッフルでの2459±1.3Maでの地球と月の距離の計算
縞状鉄鉱層(BIF)(Lantink et al。2021)は、(〜2450 Ma)Weeliの潮汐リズマイトを解読する同等の推定値と比較して、私たちのモデルと著しく一致しています。
オーストラリアのウーリBIF(Walker&Zahnle 1986; Williams2000)。
私たちのターゲットカーブは、おそらく今、ロバストを詳しく説明するために使用することができます
を導いたこれらの潮汐リズマイトの分析のための手順
時には異なる解釈に(Walker&Zahnle 1986;
ソネット&チャン1998;ウィリアムズ2000)(表D.2)。私達は手に入れました
を通じて得られた3.2GaでのaMの推定値との印象的な適合
Moodiesグループのリズマイトの分析(Eriksson&Simpson 2000; de Azarevich&Azarevich 2017)、しかし私たちは否定しません
この合意は偶然の一致である可能性があり、新しい分析
周期層序学的推定に関連するこれらのセクションのうち、
どういたしまして。大きな進展が見込まれます
近い将来、多くの周期層序の分析で
レコード。これを使用して、さらに多くの制約を加えることができます。
物理モデル。特に興味深いのは、図3の急な傾斜に対応する、共鳴状態(またはその周辺)で発生するシーケンスです。最後に、このモデルは地球と月の距離の一貫した履歴を提供するため、
月の形成シナリオの時間スケールを制約するために使用されます
(Cuk et al.´2016)。地質データ間のこの一貫性
そして、地球と月の進化の現在のシナリオも
これらの地質データの使用を促進し、特に
標準的な観測としての周期層序地質データ
太陽系の過去の歴史を回復するための窓。
地球と月の距離の共鳴潮汐進化
概要
地球と月のシステムでの潮汐相互作用により、地球のスピンが遅くなり、月が漂流します。この不況
現在、月は非常に正確に測定されていますが、50年以上前に、単純な潮汐モデルが外挿されていることがわかりました。
過去にさかのぼると、地質年代学的および地球化学的証拠とははるかに相容れない月の時代につながります。順番に
この問題を回避するために、海洋の潮汐散逸を考慮に入れて、より精巧なモデルが提案されています。しかし、これらは
モデルは、推定月齢と現在の月の後退の両方に同時に適合しませんでした。ここでは、物理的なものを提示します
これらの2つの制約を調整し、潮汐履歴の一意のソリューションを生成するモデル。このソリューションは、利用可能なものによく適合します
地球-月系の歴史のための地質学的プロキシと周期層序学の方法を統合します。結果として生じる進化
海洋散逸における共鳴の複数の交差を含み、これは、
月周回軌道距離、地球の1日の長さ、および地球の傾斜角。
キーワード。地球–月–惑星と衛星:動的進化と安定性–惑星と衛星:海
図1.過去10億年にわたる地表「古重心」の緯度の時間的進化プレートテクトニクス再構築は、Merdith et al。(2021)から採用され、
複数にわたる最初の運動学的に連続的な構造運動モデル
超大陸サイクル。 展開は、200Myrのウィンドウで移動多項式回帰フィルターを使用して赤で平滑化されます。 私たちの有効なモデルでは、この曲線は、半球形の大陸キャップの中心の進化をマッピングします。
中生代では赤道、古生代ではほぼ極性になります。

図2.χ^2の不適合面
研究された3つの幾何学的モデルについて。 地球と月のシステムの過去の動的進化は、
2つのフリーモデルパラメータHとσRの表示範囲。 不適合は、現在測定されている月の景気後退率を使用して確立されます。
LLR、および月齢(付録C)。 3つのモデルは、地史上、海洋シェルの形状が異なります。
他の2つよりも物理的なリアリズムを備えた複合モデル。 この分析の数値結果は(表C.1)に要約されています。 The
不適合の最小値のそれぞれに関連する動的進化は、図3の月の準主軸の観点からプロットされています。
図5、および図6の傾斜角と歳差運動の頻度。

図3.月の準主軸の経時変化。 地球の月の分離aMは、
図2で説明されているように、自由パラメーター(H、σR)の最適値
と本文で。 進化曲線の上にプロットされているのは、周期層序学と潮汐層データからのaMの地質学的推論です(表D.1とD.2)。 影付きのエンベロープは2σ-不確かさに対応します
結合されたモデルの適合パラメータ(付録C)。 の中に
狭いウィンドウで、進化の最新の250 Myrsをズームし、古地理的再構成を使用した明示的な数値潮汐モデリングに対応する進化と比較します(Greenetal。
2017)、および数値解法La2004(Laskar
etal。 2004)。

図4.潮汐トルクの履歴。半日周の対数
地球の潮汐トルク(現在の値で正規化:T〜 = T / T(t =
0))は時間の関数としてプロットされます。実線の曲線は
3つのフェーズを含む結合モデルのトルク:最初の
フェーズでは、半球形の海洋が地球の表面を移動し、図1の大陸の重心が進化します。
1 Gaを超える連続プレートテクトニクスモデル。フェーズ2では、
不連続性のモデリングを回避するために、半球形の海洋を1Gaの構成にします。これを超える減衰された潮汐トルクは注目に値します
位相は、固定された海洋位置によるものではなく、スペクトルの非共鳴バックグラウンドを占める潮汐応答によるものです。
この間隔に関連する潮汐周波数。 tswitchを超えて、
グローバル海洋構成のモデルのフェーズ3。破線と
一点鎖線の曲線は、指定された間隔で無視されるグローバルおよび半球形の海洋トルクにそれぞれ対応します
選択的結合モデルによる。
5.地質学研究の新しいターゲット
この記事では、最初の半解析的物理モデルを構築しました
これは、地球と月の進化における最も正確な制約、つまり現在の潮汐散逸率と月の年齢に適合します。
モデルを利用可能な地質データのいずれかに適合させることは意図的に避けています。驚くべき方法で、のユニークなソリューション
私たちの組み合わせたモデルは、大規模なセットにほぼ完全に一致します
それらの地質データ(図3および図5、6)。このソリューションは
地質学研究の新しいターゲットを提供します。それは明確に検証します
層序シーケンスから地球の歳差運動頻度を推定する周期層序アプローチ(Meyers&Malinverno 2018; Huangetal。2020;Sørensenetal。2020;Lantink
etal。 2021)(表D.1)。特に、周期層序学的評価
ジョッフルでの2459±1.3Maでの地球と月の距離の計算
縞状鉄鉱層(BIF)(Lantink et al。2021)は、(〜2450 Ma)Weeliの潮汐リズマイトを解読する同等の推定値と比較して、私たちのモデルと著しく一致しています。
オーストラリアのウーリBIF(Walker&Zahnle 1986; Williams2000)。
私たちのターゲットカーブは、おそらく今、ロバストを詳しく説明するために使用することができます
を導いたこれらの潮汐リズマイトの分析のための手順
時には異なる解釈に(Walker&Zahnle 1986;
ソネット&チャン1998;ウィリアムズ2000)(表D.2)。私達は手に入れました
を通じて得られた3.2GaでのaMの推定値との印象的な適合
Moodiesグループのリズマイトの分析(Eriksson&Simpson 2000; de Azarevich&Azarevich 2017)、しかし私たちは否定しません
この合意は偶然の一致である可能性があり、新しい分析
周期層序学的推定に関連するこれらのセクションのうち、
どういたしまして。大きな進展が見込まれます
近い将来、多くの周期層序の分析で
レコード。これを使用して、さらに多くの制約を加えることができます。
物理モデル。特に興味深いのは、図3の急な傾斜に対応する、共鳴状態(またはその周辺)で発生するシーケンスです。最後に、このモデルは地球と月の距離の一貫した履歴を提供するため、
月の形成シナリオの時間スケールを制約するために使用されます
(Cuk et al.´2016)。地質データ間のこの一貫性
そして、地球と月の進化の現在のシナリオも
これらの地質データの使用を促進し、特に
標準的な観測としての周期層序地質データ
太陽系の過去の歴史を回復するための窓。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます