
肉眼で見える彗星として有名になった紫金山アトラス彗星じゃ無い方のアトラス彗星が予想通り近日点通過せずに崩壊した、おかげで彗星核の大きさが生き残れる崩壊するを分けているようで、今後は近日点距離と彗星核の大きさが事前分かれば明るい彗星になるかどうか判断できるのではないか。大昔のサングレーサーの元になった彗星は残ってはいないけど、分裂した大彗星の残りが次々訪れそうです。以下、機械翻訳。
クロイツ彗星 C/2024 S1 (ATLAS) の消滅
2024年12月23日
抽象的な
クロイツ族のサングライジング彗星のほとんどは近日点の数日前に発見されるため、その物理的性質や崩壊を研究するための観測機会が著しく制限される。クロイツサングライジング彗星C/2024 S1(ATLAS)は、近日点距離0.008 auに到達する1か月前に発見され、地上および宇宙の望遠鏡の両方から物理的観測が可能になった。我々はノルディック光学望遠鏡を使用して0.9 auから0.4 auまでの観測結果を提示し、1)近日点前の0.7 auですでに核崩壊が進行していたこと、2)活動が距離によって予測できないほど変化したこと、3)核の半径が<600 m(赤色幾何反射率0.04と仮定)。また、STEREO-A探査機のコロナグラフ観測を使用して、太陽中心からの距離にあるC/2024 S1を研究します。
≲0.1 au。コマ散乱断面積は0.075 au付近でピークに達し、その後徐々に減衰し、〜20、0.02 auでの最後の観測に向かっている。近日点付近での減衰は、黒体温度から始まる難治性コマ粒子の昇華の結果であると解釈される。
〜1000 K で、オリビンの組成と一致しています。彗星は近日点通過後には検出されませんでした。近日点付近で核を破壊するプロセスが作用していると考え、彗星が太陽のロッシュ ローブに入る前であっても、回転不安定性と昇華損失がこの目的に向かって一緒に作用していると結論付けています。
彗星:一般 - 彗星:個別 (C/2024 S1)
† slugcomment: 2024年12月23日改訂
1 導入
彗星C/2024 S1(ATLAS)(以下S1)は、UT2024年9月27日にR.シヴァードによってATLAS調査望遠鏡(シヴァード、2024)。 S1彗星には長半径があった
a= 96.6 au、傾斜角i= 141.9°、離心率e= 0.99992。近日点距離は、q=0.0080auは1.73 R ⊙に相当し、ここでR⊙=6.96×10^8mは太陽の半径です。近日点が小さく、傾斜角が大きいことから、C/2024 S1はクロイツ太陽接近彗星群(マースデン、1967)この関連性は近日点の議論によって強化されている。
ω= 69.2°、昇交点の経度は、Ω= 347.1°であり、どちらもクロイツ彗星に似ています。クロイツ彗星は、おそらくオールトの雲から来た前駆天体の破片であり、以前の太陽への接近の結果として崩壊しました(Sekanina&Chodas(2007)、フェルナンデスら (2021))。クロイツ彗星の物理的寿命は、太陽に近づくと激しく加熱されることによって制限される。個々のクロイツ彗星の寿命の推定値は、〜10^3年(つまり、C/2024 S1の950年の軌道周期に匹敵する)であり、そのような天体の大多数が近日点を通過しないように見えるという観察と一致している(ナイトら、2010)現代のクロイツ彗星は連鎖的破砕の産物である可能性が高い(Sekanina & Chodas、2007)そして、元のクロイツ前駆核の崩壊からの経過時間は不明ですが、おそらく 10^3年よりはるかに長いと考えられます。
クロイツ彗星のほとんどは、太陽に非常に近いときに、軌道上の太陽コロナグラフ観測所(主にSOHOとSTEREO宇宙望遠鏡)によって得られたデータで発見されます。これらの太陽に焦点を当てた宇宙船は、非常に大きなピクセルを持ち、角度分解能が低いことに加えて、太陽コロナの背景の高くて変動する表面輝度によって感度が制限されます。地上データで暗い空を背景にS1が早期に発見されたのは、太陽から1auのときで、〜UT 2024 10月28日の近日点の1か月前に、地上の夜間望遠鏡でより高解像度で感度の高い観測を行う機会が得られました。太陽のまぶしさで地上から見えなくなった後も、STEREO Cor-2A宇宙コロナグラフを使用して観測を続けました。(SOHO宇宙船からの同時期のLASCOコロナグラフ観測は、執筆時点では「クイックルック」(未較正)形式でのみ公開されていました。未較正のLASCO画像を調べたところ、彗星は近日点付近で飽和していることが示されたため、本研究ではこれらのデータを使用しませんでした)。私たちの科学的目的は、太陽に接近する彗星の進化と崩壊を前例のない詳細さで調べることでした。
2 観察
NOTデータ:スペインのラスパルマ島、高度2.4kmにある直径2.56mのノルディック光学望遠鏡(NOT)を使用してS1を撮影しました。この能動光学望遠鏡は地平線から10°以内を観測できるため、比較的小さな太陽離角にある天体の薄明研究に非常に役立ちます。ALFOSC(アルハンブラ微弱天体分光器およびカメラ)イメージャーを使用しました。このイメージャーは、約6.5フィートの範囲で0.21″ピクセル-1の画像スケールを提供します。
×6.5フィートの視野。画像は広帯域ベッセルRフィルター(中心波長)を使用して撮影されました。
λc= 6500Å、FWHM = 1300Å)を測光監視の目的で設置した。近日点通過前の観測時間は、各セッションの開始時の高度制限と終了時の薄明開始によって、1晩あたり最大約20分に制限された。この期間に、60秒間の画像が6~8枚取得されたが、10月20日までに30秒間の画像が2枚に減少した。画像は非恒星速度(例:〜彗星の動きを追うために、10月3日の200″時-1分に撮影し、不良ピクセルから保護するために露出の間にディザリングを行った。10月19日のUTより前は、フィールドスターとオートガイダーを使用して望遠鏡の非恒星追跡を制御した。その日以降は、オートガイダー(空が明るくなるとうまく機能しなかった)を放棄し、非恒星速度でガイドなしの画像を取得しました。測光較正には、ランドルト標準星の画像と、Pan-STARRS測光カタログで観測されたフィールドスターの画像を使用しました。典型的なシーイングは、〜1″ FWHM から 5″ まで。解析では、最も悪いシーイング データを除外しました。フラット フィールドの露出は、NOT ドームの内側の照明パッチを使用して毎晩取得されました。NOT 観測の記録は、表1に示されています。
測光は、固定された線形(角度ではない)スケールの円形投影開口部内で行われた。変動するシーイングとコマの角度スケールを考慮して、彗星の距離に投影された半径5000 km、10,000 km、15,000 kmの開口部を測定することを選択した。
R5、R10そしてR15、それぞれです。スカイ減算は、測光環に比べて大きい同心円環内の中央信号から取得されました。彗星の尾は、いくつかのフィールド星の軌跡と同様に、スカイ環を横切っています。これらの信号がすべて、スカイ領域内の中央値を使用して効果的に除去されていることを確認しました。
図1にサンプルの合成画像を示します。初期の観測では、シーイングと空の明るさの変動による夜ごとの違い以外に、形態的または測光的変化の証拠はほとんど見られませんでした。図1の 10 月 6 日の画像は、放射圧スイープ彗星の典型的な形態を示す代表的なものです。UT 2024 の 10月 11日までに、尾の軸に沿った離散構造の存在から、崩壊の明確な証拠が明らかになりました。これは、図1の等輝度線の延長として見られ、図2のより詳細なビューで強調されており、少なくとも 4 つのコンポーネントが明らかになっています。これらの離散構造は UT 10 月 17 日までに消え、その時までに見かけの明るさは 100% 増加しました。
〜
1.5等級の明るさで、おそらく崩壊による新鮮な氷の露出に関連している。10月19日のUTの観測では、彗星は再び明るくなり、
R15= 9.2 で、10月 4日から 11日のプラトーレベルよりも約 5.5等級 (160 倍) 明るくなりました。この増光は部分的には塵の生成量の増加を反映しており、顕著な形態変化 (図1 ) を伴い、球形の頭部と細長い尾から、太陽 - 彗星線に垂直な「翼」を持つ、より鈍い太陽に面したコマへと変化しました。同様の翼のある形態は他の彗星 (特にサングライザー C/2012 S1 (ISON)) でも観測されており、原因は明らかではありませんが、近接した複数の発生源の相互作用に関連している可能性があります(Samarasinha ら、2015)。
彗星のスペクトルrH≲2 au は、核とコマの塵から散乱された太陽光による連続光と、ガスコマ内の分子からの共鳴蛍光発光の両方から構成されます。彗星分子の光破壊寿命は、rH2 C/2024 S1のような太陽近傍の彗星では非常に短い。さらに、彗星種(例えばCN、C 2、C 3)からのガス放出帯は、短い可視波長に集中している(Herzberg、1950)であり、主に B および V 広帯域フィルターを汚染します。ここでは、放射の大部分が彗星の塵から散乱した太陽光であると想定して、R フィルターの光度測定のみを分析します。
絶対等級は、彗星の等級を
rH=Δ= 1 au およびα= 0°。固定線状開口測光の場合、見かけの等級と次の式で関係する。

どこΦ(α)位相角に対応する位相関数である
α(正規化してΦ(0)=1)。NOT観測の位相角は比較的大きく(51°~65°:表1)、(測定されていない)位相関数を考慮する必要がある。便宜上、Schleicher 1による表を使用したが、結果はMarcus(1986幸運なことに、角度依存性が最も強く、不確実性が最も大きいのは
Φ(α)前方散乱ジオメトリに限定される(α≳120°)と感度α
NOTデータの範囲は控えめです。例えば、シュライヒャー曲線は、Φ(50°)= 0.38からΦ(90°)= 0.54。それでも、S1 の位相関数は測定されたものではなく仮定された量であることに留意し、2 倍の誤差が生じる可能性が十分にあると予想します。
図3は絶対等級ではないことを示しています。等級の変化は、彗星の場合に広く行われているように、太陽中心からの距離の単純なべき乗関数では表すことができません。代わりに、H最初は各開口部がフェードインし、〜10月3日(rH10月11日(0.725 au)まで減少したが、10月17日(0.544 au)までに減少に転じ、〜
10月19日までに3.5等級(0.476 au)まで明るさが上昇する。
Δ(5−10)=R5−R10、 そしてΔ(10−15)=R10−R15そしてΔ(5−15)=R5−R15
は、核からの距離の関数として測定されたコマ表面輝度の急峻さの大まかな尺度を提供し、値が小さいほど表面輝度プロファイルが急峻であることを示します。図3 は、10月17日と 19日に 3 つの差がすべて縮小していることを示しています。これは、核からの新鮮な物質の放出によって表面輝度プロファイルが急峻になっていることと一致しています。
彗星のRバンド絶対等級は散乱断面積と関係があり、Cによる

どこPR Rバンドの幾何アルベドであり、Hは絶対等級である。S1の幾何学的アルベドは測定されていないので、
pR= 0.04であり、他の彗星と同等である。
メートルR、Hおよび断面C表3にまとめました。
表3の大きく変化する断面積は、核ではなくコマ内の彗星塵による散乱を反映している。近日点前核の最も厳しい制限は、最小の断面積によって設定される。
C5= 17 km^2、UT 2024年10月11日に測定。等面積円の半径はrn=(C5/π)1/2〜2.3 km は、測光における塵の混入により、核の近日点前半径に強い上限を設定します。
近日点通過前の核半径にもっと厳しい制限を課すために、10月11日の破片測光を調べました(図2)。この日、彗星は少なくとも4つの別個の源をダストテールに埋め込んでいます。これらのうち最も東にある成分Aが主核で、他の源はガス放出力によって太陽から押しのけられた破片であると想定しています。成分Bが成分Aよりも明るいのは驚くことではありません。なぜなら、各成分の明るさはダストからの散乱によって支配されているからです。半径5ピクセル(1.1インチ)の絞りを使用すると、成分Aの見かけの等級は次のようになります。
m5= 19.0、絶対等級H5= 18.4。これらの数値の不確実性は、主に系統的誤差(例えば、小さな開口部や測定されていない位相関数によって引き起こされる)によって決まります。式2の断面積はC= 1.1 km^2、半径の円の面積に等しいrn= 600 m。厳密に言えば、コンポーネント A は明らかに非恒星であるため、これは依然として核の半径の上限です。
UT 2024 11月6日と10日に、近日点通過後に残っている可能性のあるS1の残骸を探すために、追加のNOT画像を取得しました。薄暮時に撮影された画像には、点光源の等級制限があり、彗星の兆候は見られません。
11月6日にmR>18.2、11月10日のmR>19.5。この日のエフェメリス精度(JPL Horizonsより)は1σ〜±12インチは、6.5フィートのALFOSC視野に比べて小さいため、指向性は問題にならないはずです。生き残った核のサイズを制限するために、C型小惑星位相関数を想定しました。これは、−2.5log10 (Φ(α))= この2つの日付で2.6等級と2.5等級(表1参照)α= 0°。近日点後の核の絶対等級の限界は
HR>17.2 およびHR>11月6日と10日のUTではそれぞれ18.1である。11月10日のより厳しい観測値を用いると、式2は散乱断面積の限界を与える。
C<1.4 km ^2(球半径に相当)
rn<核半径の限界は、近日点通過前の測光から決定された半径の限界と本質的に同じです。したがって、近日点通過後のデータから核が破壊されたと結論付けることはできませんが、核が検出されなかったことは、この可能性と一致しています。
STEREO COR-2Aデータ: NOTのデータに加えて、NASAの太陽観測衛星STEREO-A ( Howard et al. (2008)、Eyles et al. (2009))。我々は、外部から遮蔽されたLyotコロナグラフであるCOR-2Aカメラのデータを使用した。これは、〜2~15 R ⊙。COR-2Aカメラの画像スケールは14.7″ピクセル-1(つまり、各ピクセルは立体角を占める)です。〜ALFOSCデータよりも4700倍大きい)と有効波長〜7000Å、1000Å幅のバンドパス。Cor-2Aの画像は、強力で高度に構造化された可変的なコロナ背景の影響を受けています。コロナを抑制するために、まず10月27日から28日に撮影された114枚のCOR-2A画像から各ピクセルの最小輝度値を見つけ、この画像を個々の画像から減算しました。次に、6秒間積分したCOR-2A画像を通常5枚から6枚の画像の中央グループに結合し、より優れた信号対雑音比のデータを提供しました。画像の位置合わせは、フィールドの星とS1のJPL Horizonsエフェメリスを使用して行いました。また、測光較正のために、彗星データと同じ方法で処理されたフィールドの星の恒星位置合わせされた合成画像を使用しました。彗星は10月27日にCOR-2Aフィールドに入り、約24時間見え続けました。STEREO-A観測の記録を表2に示し、結合した画像を図4に示します。
宇宙望遠鏡から彗星までの距離は、〜STEREO-A観測が行われた1日間。そのため、固定角度半径5ピクセルと10ピクセル(74″と147″)の円形投影アパーチャを使用し、外半径50ピクセル(735″)の連続した環状部内で計算された中央信号からの背景減算を行った。5ピクセルと10ピクセルのアパーチャ半径は、彗星でそれぞれ48,000 kmと96,000 kmに相当する。これらのアパーチャからの等級を次のように呼ぶ。
R48そしてR96天空開口部の中央信号の使用により、彗星の尾からの光が適切に除去され、残留コロナ背景が適切に表現されていることを確認しました。
測光は5ピクセルと10ピクセルの開口部内の絶対等級を見つけるために補正されました。
H48そしてH96、それぞれ上記の通り(表4)。図5は、彗星が約rH= 0.075 au (16 R ⊙ )。その後、約2等級ずつ減光し、最後に検出されたのは
rH= 0.019 au (4.1 R ⊙ )、近日点の 0.008 au (1.7 R ⊙ ) のわずか 2.3 時間前です。
また、近日点通過後のCOR-2A画像合成も調べ、S1の残存物を探しました。UT2024年10月29日02時53分までに取得された画像(rH= 0.074 au または 16 R ⊙)は S1 の証拠を示さず、その後、彗星の天体位置はコロナグラフの視野外になりました。
3議論
NOTとSTEREO-Aの観測結果から、
1) 近日点通過前の絶対等級は10月3日から10月11日までの期間のNOTデータで大きく変化した(rH= 0.937 au から 0.460 au までの範囲で変化しましたが、単純なべき乗則型の依存性はなく、最初は暗くなり、その後突然明るくなりました。
2) 10月11日に撮影された破片(rH= 0.725 au; 図2 ) は、核が近日点よりずっと前に崩壊していたことを示しています。
3) 近日点前核半径はrn= 600 m (アルベド 0.04 と仮定)
4) STEREO-Aデータにおける絶対輝度のピークは10月27日で、
rH= 0.075 au (〜16 R ⊙)。その後、彗星は10月28日の最後の近日点通過前観測まで暗くなり、rH= 0.02 au (4.1 R ⊙ )。
5) 彗星は近日点通過後にはSTEREO A観測でも、より感度の高いNOT地上データでも検出されなかった(表1)。近日点通過後のNOTデータから、残存するコンパクト核の大きさに上限が示された。rn≤700 m(アルベド0.04と仮定)。
3.1物理的プロセス
C/2024 S1 の外観と測光の変化に影響を与える可能性のある物理プロセスについて簡単に考察します。
岩石の昇華:球状の等温黒体の平衡温度は、
TBB=278rH^−1/2は、図5の上軸に沿って示されています。S1彗星は、rH〜0.075 au (16 R ⊙ )、これはTBB〜1000 K です。小さな粒子 (黒体ピークの波長よりも半径が小さい粒子) は、放射率が低いため、さらに高い平衡温度まで上昇します。1000 K を超える温度は、露出した水氷が生き残るには高すぎますが、より耐火性の高い物質の昇華と一致します。例として、オリビンは彗星のコマに豊富に存在することが知られています(Zolensky ら、2024)であり、オリビンの昇華距離は0.07 au(〜15 R ⊙ ) (小林ら、2011)は、明るさのピークの位置と非常によく似ている。オリビンまたは同様の昇華潜熱を持つ他の物質のコマ粒子の昇華は、図5に見られるS1の近日点付近での減衰を説明する可能性が高い。太陽に接近する彗星は、一般的に、近日点付近で見かけの等級が最大になる。
〜10~14 R ⊙ (ナイトら、2010これは核の完全な溶解を表すと解釈されてきたが、コマ粒子の昇華は、追加の、そして確かに避けられない説明を提供する。
β流星体は、太陽から10~20 R ⊙ の距離にある黄道塵粒子の昇華によって発生します(Szalay et al.、2021)。
S1の核にはほんのわずかな部分しか存在しないことに注意することが重要です(≲全体の(コマが支配的な)散乱断面積の 0.1% です。したがって、彗星の近日点付近での減衰から核が破壊されたと結論付けることはできませんが、その可能性を否定することもできません。
伝導:熱伝導はS1の核の破壊には重要ではない。これを確認するには、経過時間に注目してください。
τ熱は距離を越えて伝導する d〜(κτ)^1/2、伝導前面の有効速度は、Vc=d/τは次のように与えられる。
Vc〜(κ/τ)^1/2。 ここ、κは熱拡散率であり、彗星に見られる多孔質物質の場合、値は
κ〜10^−9m^ 2 s^ -1。τ〜150日(1.3×10^7 3 auの水の昇華線を通過する時点と近日点の間の距離を計算すると、
d〜0.1 m、平均伝導前線速度はヴc〜8×10^−9ms^ -1。このように薄い表面層から氷が失われても、核全体の安定性や存続には何の影響も及ぼさない可能性がある。
氷の昇華: S1からの質量損失は、昇華による表面のアブレーションによって支配される。
rH≲1 auの場合、太陽に垂直に露出した完全に吸収する平坦な水氷表面からの平衡昇華率は、エネルギーバランスによって次のように表される。

どこL⊙= 4×10^26Wは太陽の光度、rHは太陽中心からの距離であり、H=2.8×10^6J kg -1は昇華潜熱である。例えば、距離が
rH= 1.0 au(表1参照)、式3はfs〜0.5×10^−3kg m -2 s -1。かさ密度は
ρ= 500 kg m^ -3 ( Groussinらによる彗星核の公称密度(2019) 、氷の表面が昇華によって後退する速度、
Vs=fs/ρ、 はどこL⊙= 4×10^26Wは太陽の光度、rHは太陽中心からの距離であり、H=2.8×10^6J kg^ -1は昇華潜熱である。例えば、距離が
rH= 1.0 au(表1参照)、式3はfs〜0.5×10^−3kg m^ -2 s^ -1。かさ密度はρ= 500 kg m^ -3 ( Groussinらによる彗星核の公称密度(2019) 、氷の表面が昇華によって後退する速度、Vs=fs/ρ、 はVs〜1×10^−6ms^−1、伝導前線の速度よりも約2桁速い。このため、S1の表面の氷からの昇華により、下から冷たい氷が継続的に露出することになる。
これをさらに詳しく調べるために、S1が太陽中心から遠距離から近日点まで移動する際の累積的な氷の損失を計算した。Vs〜1×10^−6ms^−1、伝導前線の速度よりも約2桁速い。このため、S1の表面の氷からの昇華により、下から冷たい氷が継続的に露出することになる。
これをさらに詳しく調べるために、S1が太陽中心から遠距離から近日点まで移動する際の累積的な氷の損失を計算した。

どこΔZ(rH)遠日点から遠距離に移動する際に失われる氷層の厚さですrH、t0遠日点における時間であり、t彗星が到達した時間です
rH我々は、rHそしてtケプラー方程式の数値解法と計算によってfs昇華平衡方程式から

どこAそしてϵ氷のボンドアルベドと赤外線放射率です。Aまたはϵは知られているが、その影響はfs無視できるほど小さいA≪1とϵ〜1. 私たちは仮定した
A= 0 かつϵ= 1. エネルギーバランス計算には幾何学的補正を含めました。γ(rH)= 1−(r⊙/rH)^2太陽の半球全体がS1から見えないという事実を説明するために、rH/R⊙小さい。(この幾何学的補正は周辺減光の影響を無視しており、rH/r⊙→1なので、概算値として考えなければならない。しかし、ΔZいずれにしても、彗星が太陽に接近する時間は非常に短いので、この値は小さい。シュテファン・ボルツマン定数はσ=5.67×10^−8W m^ -2 K^ -4 . 数量χは、核表面上の熱の空間分布を反映する無次元パラメータである。太陽-彗星線に垂直な平面の場合、
χ= 1 一方、昼側のみ加熱された球状核の場合、χ= 2であり、等温球の場合は、χ= 4. 彗星は主に太陽に面した熱い側から昇華することが知られているので、後者の制限は無視し、χ= 1 と 2。
式5は水氷の質量昇華フラックスについて反復的に解かれた。fs(rH)図6にプロットされた結果は、2つの照明ケースを示しています。青い実線は、
χ= 1。与えられた条件における最大可能温度と昇華速度を表す。rHは、S1の太陽直下の点の高温にほぼ相当する。破線の赤い曲線は、χ= 2。
曲線は類似しており、式3に基づく推定と一致している。図6は、遠日点から1 auまでの氷の累積損失がΔZ〜数メートル、近日点まで延長すると損失が近づく
ΔZ〜50 mから100 m。近日点に向かう途中での抑制されない昇華は、半径50 mから100 m未満の核を破壊する可能性があり、これは、一般的に小さいクロイツ彗星のほとんどの消滅のもっともらしい(ただし、唯一の原因ではない - 以下を参照)原因である(ナイトら、2010)の計算では
Δず明らかに理想化されていますが、近日点距離が小さいことによる熱の影響が大きいことを示しています。
回転不安定性:昇華する核からの異方的な質量損失は、回転を変えるトルクを及ぼします。十分な時間が与えられると、このトルクは回転を不安定な点まで加速させます。短周期彗星の最近の測定では、流出運動量は主に核の半径方向ですが、中央値の割合、
KT〜0.7%、核を回転させる(Jewitt、2021)。核を初期半径の球体とみなすと、rn、 密度ρ、角周波数で回転するωスピン角運動量は次のように表される。L=(2/5)Mnrn^2ω、 どこMn=4πρrn^3/3は核質量であり、

厚さの殻の質量ΔrはΔm=4πrn^2ρΔr、その直線運動量は、速度で放出されたときⅤthはΔmⅤth
そして、殻の放出による角運動量の変化はΔL=ΔmVthKTrn、 または

設定
ΔL=Lを表す式を与える
Δr、原子核の角運動量を大幅に変化させるために失われなければならない殻の厚さ、

評価する
Δr私たちは設定しました
rn= 600 m、近日点前測光法で許容される最大値。コマ膨張速度は
rH= 1 auとしてⅤth〜500 ms^ -1、これは300 Kの水分子の熱速度に等しい。S1の核の角周波数は不明だが、ほとんどの彗星核の自転周期は2倍以内である。
〜10時間(ω〜1.7×10^−4s^ -1 ) (ココタネコバら、2017)を代入すると、半径600mの核はわずか1層しか昇華する必要がないことがわかります。
Δr= 2.3 mの厚さで、回転を2倍に変化させます。図6は、太陽中心からの距離が2.3 mに達する累積昇華損失を示しています。
rH= 0.5 auから1.1 au(表面温度の空間分布に依存する)であり、
〜0.7 auの距離で、S1は初めて断片化した外観(図2)と劇的な明るさの急増(図3)を示しました。これは、核がこれらの近日点前距離で回転不安定性に達したことの証拠ではありませんが、核が構造的に凝集していないと仮定すると、この推論は確かにもっともらしいものです。
式8は、Δrスケールはrn^2そのため、核の半径が600メートルより小さければ、さらに薄い表面層の放出によるトルクが核を回転させるのに十分なものとなり、さらに大きな太陽中心距離でも崩壊が始まる可能性がある。ほとんどのクロイツ彗星は小さい(数個から〜50mの物体は近日点まで生存できない。式8に従うと、50mの物体は〜2cmの氷の損失は、ガス放出トルクによってその回転が実質的に変化するには十分である。図6は、小惑星帯の距離でも2cmの氷の損失が起こり得ることを示し、ほとんどの小さなクロイツ彗星が発見されるずっと前から崩壊が始まっている可能性があることを示唆している。急速な自転が主に
<100 m の物体(Warner et al.,2009)、回転崩壊に対する生存は有限の凝集強度の役割を反映している可能性がある。
一方、式8は、非常に大きなクロイツ彗星の核は、近日点に向かう途中で昇華する機会が限られているため、回転による崩壊に耐えられるはずであることを示している。
Δr= 50 mから100 m(近日点までの最大累積昇華損失、図6を参照)を式8に代入し、他のパラメータは上記と同じとすると、近日点に向かう途中で回転できる最大の核の半径は次のように表される。
rn= 2.8 kmから3.9 km。残念ながら、最大のクロイツ彗星核の大きさは観測的によく決定されていません。サングレーザーC/2011 W3(ラブジョイ)は近日点近くで崩壊したようです。その核の大きさは不確かですが、ほぼ確実に1 km未満でした(レイモンドら、2018ナイトら(2010)の表1には、近日点通過後の彗星C/1965 S1(池谷・関)の半径(これも非常に不確か)が4.3キロメートルと記載されている。大きなクロイツ彗星は、C/1965 S1 (セカニナ、1966)ですが、回転バーストによって破壊される可能性は低いです。
これらの考察は明らかに非常に粗雑である。核は球形ではない可能性があり、質量は表面殻から均一に失われる可能性は低く、
KT短周期彗星で測定された(Jewitt、2021) はS1 には当てはまらない可能性があり、構造的には弱いものの、回転による破裂に抵抗するのに十分な強度がある可能性がある。とはいえ、ガス放出トルクによるスピンアップは、この彗星や他の 1 キロメートル未満の太陽接近彗星の分裂のもっともらしい原因であり、核破壊への素早い道筋となる。核を分裂に向かわせるには表面が数メートル失われるだけでよいため、回転破壊は核破壊につながる最も効率的な経路である。
ロッシュ不安定性: 太陽の重力の核直径にわたる勾配は、ロッシュ距離内での混乱の潜在的な原因である。

どこΓは無次元定数であり、ρ⊙= 1300 kg m^-3は太陽の密度です。強度のない球体の場合、Γ〜2.4、そして
ρ= 500 kg m^-3式9はrR/R⊙〜3.3. これは近似値に過ぎない。なぜなら、原子核は強度がないか球状である可能性は低く、また式9では原子核の回転による不安定化の影響も無視しているからである。不安定距離はこれよりも大きいか小さいかのどちらかである。
rR/R⊙〜3.3 潮汐力の強さ、形状、回転によって変動します。しかし、近日点付近(rH/R⊙〜1.7)は、木星のロッシュ球に入ったときに分裂した彗星D / 1993 F2(シューメーカー-レヴィ9)の場合と同様に、S1の見かけ上の消滅に寄与した可能性が高い(Asphaug&Benz、1996)、そしてC/1965 S1(池谷・関)は、0.008 au近日点(セカニナ、1966)。
S1彗星は、発見されるほど明るかったという点で珍しい。
〜1 auであるのに対し、クロイツ彗星のほとんどは小さすぎる(半径数auから〜50 m (ナイトら、2010) ) であり、この距離では検出できないほど暗い。S1の早期検出は、その核が平均よりも大きいことを示唆しており、経験的な上限は
rn<600m。さらに大きなクロイツ彗星もいくつか知られている。例えば、C/2012 S1(ISON)の核は600m≤rn≤900 m (Lamy et al.,2014)とやや大きい。
そして最も有名なクロイツ彗星であるC/1965 S1(池谷・関)はおそらく
この彗星の核の大きさに関する信頼できる推定値は存在しないが、半径は>1 kmである。ほとんどのクロイツ彗星は近日点前か近日点近くで消滅し、C/2024 S1やC/2012 S1(ISON)も同様である(Keane et al.、2016回転とアブレーションによる破壊を生き延びるのに十分な大きさの太陽接近型天体だけが、太陽のロッシュ球に入ると、重力による破壊の最後の試練(式9)に直面する。
4まとめ
地上および宇宙望遠鏡によるクロイツ彗星C/2024 S1の光学観測では、
1. 近日点前核半径はrn<600 m (赤色幾何反射率 0.04、C 型位相関数を想定)。近日点前 0.7 au までに核の複数の成分への崩壊が進行していた。
2. 地上で行われた幾何学補正測光では、太陽中心からの距離に単純に依存せず、彗星は最初は〜0.9 au から 0.7 au にかけて 1 等級明るくなり、その後 0.45 au に向かって 3.5 等級明るくなり、非平衡質量損失を示しています。
3. STEREO-Aによる太陽近傍の測光によると、S1は0.075 au付近でピーク輝度に達し、放射温度は〜1000 K で、近日点に向かう途中で暗くなっていった。粒子の昇華がこの近日点付近での暗化を説明できるかもしれない。
4. ガス放出トルクによって引き起こされる回転不安定性は、この彗星や他のクロイツ彗星の太陽に接近する最も効率的な破壊メカニズムであり、次に昇華によるアブレーション損失が続く。近日点に向かう途中で回転破壊とアブレーションを生き延びた核破片は、太陽のロッシュ球に入ると破壊されたであろう。

図 1.— 3 日間の NOT 画像から得た C/2024 S1 の近日点通過前の外観。スケール バーと方向矢印は 6 つのパネルすべてに共通です。

図 2.— UT 2024
10 月 11 日、rH = 0.725 au における C/2024 S1 の近日点通過前の外観を示す NOT 画像。上部の画像は、60 秒積分の各 5 枚の画像の中央値からコンパイルされた生データを示しています。この画像のガウス平滑化バージョンが中央のパネルに表示され、差分画像が下部に表示されます。4 つの個別のオブジェクトにラベルが付けられています。スケール バーと基本方向がマークされています。
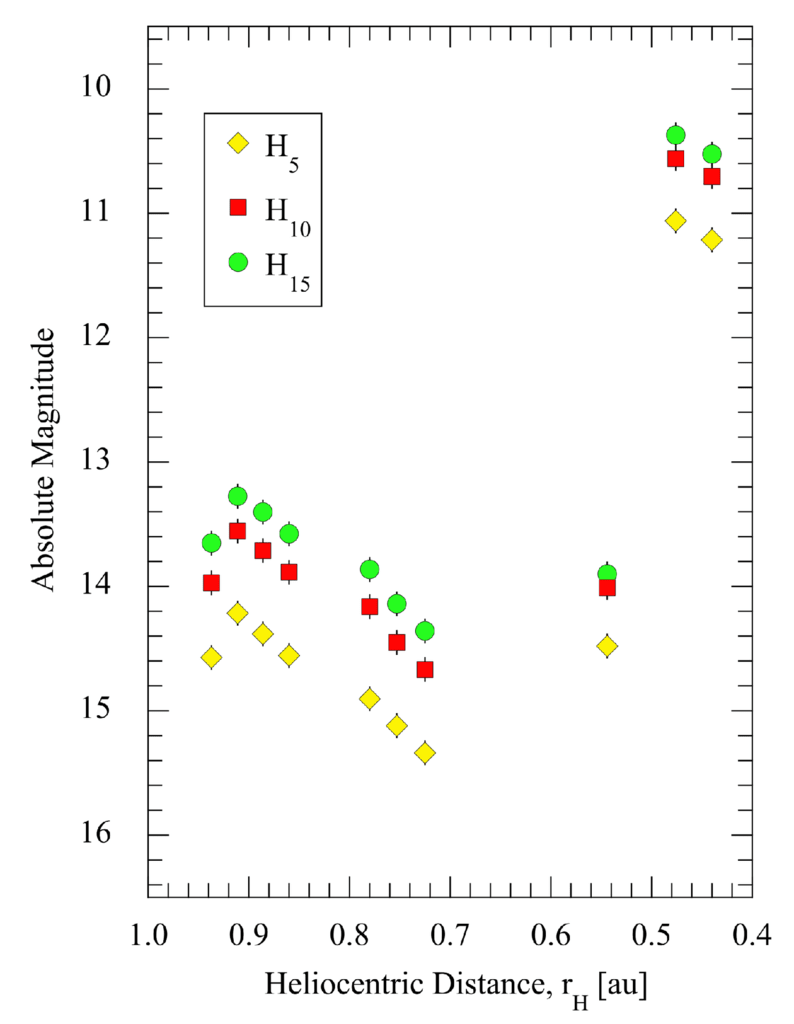
図 3.— 近日点通過前 NOT 観測の絶対等級と太陽中心距離の関係。固定投影半径 5,000 km (黄色のダイヤモンド)、10,000 km (赤い四角)、15,000 km (緑の円) の円形開口部内で測定。

図 4.— Cor-2A 合成画像。各パネルは上が北、左が東で、幅は約 1◦ (彗星の位置で 2.4×10^6 km) です。0.039 au および 0.047 au パネルの黄色の目盛りは、近日点通過後の彗星の予想される位置を示していますが、この距離では観測されていません。

図 5.— 太陽中心からの距離の関数としての COR-2A データからの測光値。
絶対等級は、半径 48,000 km (青いダイヤモンド) と 96,000 km (赤い円) の開口部内に表示されます。等温球状黒体温度は、上軸に沿ってマークされています。垂直の破線は近日点を示しています。

図 6.— 2 つの昇華モデルにおける、太陽中心からの距離が減少するにつれて増加する累積氷の融解 (青の実線) 太陽-彗星線に垂直に向いたスラブと、(赤の破線) 太陽に面した半球からのみ昇華する球状の氷表面。
C/2024 S1 の軌道と氷の密度 ρ = 500 kg m^−3 と仮定。
クロイツ彗星 C/2024 S1 (ATLAS) の消滅
2024年12月23日
抽象的な
クロイツ族のサングライジング彗星のほとんどは近日点の数日前に発見されるため、その物理的性質や崩壊を研究するための観測機会が著しく制限される。クロイツサングライジング彗星C/2024 S1(ATLAS)は、近日点距離0.008 auに到達する1か月前に発見され、地上および宇宙の望遠鏡の両方から物理的観測が可能になった。我々はノルディック光学望遠鏡を使用して0.9 auから0.4 auまでの観測結果を提示し、1)近日点前の0.7 auですでに核崩壊が進行していたこと、2)活動が距離によって予測できないほど変化したこと、3)核の半径が<600 m(赤色幾何反射率0.04と仮定)。また、STEREO-A探査機のコロナグラフ観測を使用して、太陽中心からの距離にあるC/2024 S1を研究します。
≲0.1 au。コマ散乱断面積は0.075 au付近でピークに達し、その後徐々に減衰し、〜20、0.02 auでの最後の観測に向かっている。近日点付近での減衰は、黒体温度から始まる難治性コマ粒子の昇華の結果であると解釈される。
〜1000 K で、オリビンの組成と一致しています。彗星は近日点通過後には検出されませんでした。近日点付近で核を破壊するプロセスが作用していると考え、彗星が太陽のロッシュ ローブに入る前であっても、回転不安定性と昇華損失がこの目的に向かって一緒に作用していると結論付けています。
彗星:一般 - 彗星:個別 (C/2024 S1)
† slugcomment: 2024年12月23日改訂
1 導入
彗星C/2024 S1(ATLAS)(以下S1)は、UT2024年9月27日にR.シヴァードによってATLAS調査望遠鏡(シヴァード、2024)。 S1彗星には長半径があった
a= 96.6 au、傾斜角i= 141.9°、離心率e= 0.99992。近日点距離は、q=0.0080auは1.73 R ⊙に相当し、ここでR⊙=6.96×10^8mは太陽の半径です。近日点が小さく、傾斜角が大きいことから、C/2024 S1はクロイツ太陽接近彗星群(マースデン、1967)この関連性は近日点の議論によって強化されている。
ω= 69.2°、昇交点の経度は、Ω= 347.1°であり、どちらもクロイツ彗星に似ています。クロイツ彗星は、おそらくオールトの雲から来た前駆天体の破片であり、以前の太陽への接近の結果として崩壊しました(Sekanina&Chodas(2007)、フェルナンデスら (2021))。クロイツ彗星の物理的寿命は、太陽に近づくと激しく加熱されることによって制限される。個々のクロイツ彗星の寿命の推定値は、〜10^3年(つまり、C/2024 S1の950年の軌道周期に匹敵する)であり、そのような天体の大多数が近日点を通過しないように見えるという観察と一致している(ナイトら、2010)現代のクロイツ彗星は連鎖的破砕の産物である可能性が高い(Sekanina & Chodas、2007)そして、元のクロイツ前駆核の崩壊からの経過時間は不明ですが、おそらく 10^3年よりはるかに長いと考えられます。
クロイツ彗星のほとんどは、太陽に非常に近いときに、軌道上の太陽コロナグラフ観測所(主にSOHOとSTEREO宇宙望遠鏡)によって得られたデータで発見されます。これらの太陽に焦点を当てた宇宙船は、非常に大きなピクセルを持ち、角度分解能が低いことに加えて、太陽コロナの背景の高くて変動する表面輝度によって感度が制限されます。地上データで暗い空を背景にS1が早期に発見されたのは、太陽から1auのときで、〜UT 2024 10月28日の近日点の1か月前に、地上の夜間望遠鏡でより高解像度で感度の高い観測を行う機会が得られました。太陽のまぶしさで地上から見えなくなった後も、STEREO Cor-2A宇宙コロナグラフを使用して観測を続けました。(SOHO宇宙船からの同時期のLASCOコロナグラフ観測は、執筆時点では「クイックルック」(未較正)形式でのみ公開されていました。未較正のLASCO画像を調べたところ、彗星は近日点付近で飽和していることが示されたため、本研究ではこれらのデータを使用しませんでした)。私たちの科学的目的は、太陽に接近する彗星の進化と崩壊を前例のない詳細さで調べることでした。
2 観察
NOTデータ:スペインのラスパルマ島、高度2.4kmにある直径2.56mのノルディック光学望遠鏡(NOT)を使用してS1を撮影しました。この能動光学望遠鏡は地平線から10°以内を観測できるため、比較的小さな太陽離角にある天体の薄明研究に非常に役立ちます。ALFOSC(アルハンブラ微弱天体分光器およびカメラ)イメージャーを使用しました。このイメージャーは、約6.5フィートの範囲で0.21″ピクセル-1の画像スケールを提供します。
×6.5フィートの視野。画像は広帯域ベッセルRフィルター(中心波長)を使用して撮影されました。
λc= 6500Å、FWHM = 1300Å)を測光監視の目的で設置した。近日点通過前の観測時間は、各セッションの開始時の高度制限と終了時の薄明開始によって、1晩あたり最大約20分に制限された。この期間に、60秒間の画像が6~8枚取得されたが、10月20日までに30秒間の画像が2枚に減少した。画像は非恒星速度(例:〜彗星の動きを追うために、10月3日の200″時-1分に撮影し、不良ピクセルから保護するために露出の間にディザリングを行った。10月19日のUTより前は、フィールドスターとオートガイダーを使用して望遠鏡の非恒星追跡を制御した。その日以降は、オートガイダー(空が明るくなるとうまく機能しなかった)を放棄し、非恒星速度でガイドなしの画像を取得しました。測光較正には、ランドルト標準星の画像と、Pan-STARRS測光カタログで観測されたフィールドスターの画像を使用しました。典型的なシーイングは、〜1″ FWHM から 5″ まで。解析では、最も悪いシーイング データを除外しました。フラット フィールドの露出は、NOT ドームの内側の照明パッチを使用して毎晩取得されました。NOT 観測の記録は、表1に示されています。
測光は、固定された線形(角度ではない)スケールの円形投影開口部内で行われた。変動するシーイングとコマの角度スケールを考慮して、彗星の距離に投影された半径5000 km、10,000 km、15,000 kmの開口部を測定することを選択した。
R5、R10そしてR15、それぞれです。スカイ減算は、測光環に比べて大きい同心円環内の中央信号から取得されました。彗星の尾は、いくつかのフィールド星の軌跡と同様に、スカイ環を横切っています。これらの信号がすべて、スカイ領域内の中央値を使用して効果的に除去されていることを確認しました。
図1にサンプルの合成画像を示します。初期の観測では、シーイングと空の明るさの変動による夜ごとの違い以外に、形態的または測光的変化の証拠はほとんど見られませんでした。図1の 10 月 6 日の画像は、放射圧スイープ彗星の典型的な形態を示す代表的なものです。UT 2024 の 10月 11日までに、尾の軸に沿った離散構造の存在から、崩壊の明確な証拠が明らかになりました。これは、図1の等輝度線の延長として見られ、図2のより詳細なビューで強調されており、少なくとも 4 つのコンポーネントが明らかになっています。これらの離散構造は UT 10 月 17 日までに消え、その時までに見かけの明るさは 100% 増加しました。
〜
1.5等級の明るさで、おそらく崩壊による新鮮な氷の露出に関連している。10月19日のUTの観測では、彗星は再び明るくなり、
R15= 9.2 で、10月 4日から 11日のプラトーレベルよりも約 5.5等級 (160 倍) 明るくなりました。この増光は部分的には塵の生成量の増加を反映しており、顕著な形態変化 (図1 ) を伴い、球形の頭部と細長い尾から、太陽 - 彗星線に垂直な「翼」を持つ、より鈍い太陽に面したコマへと変化しました。同様の翼のある形態は他の彗星 (特にサングライザー C/2012 S1 (ISON)) でも観測されており、原因は明らかではありませんが、近接した複数の発生源の相互作用に関連している可能性があります(Samarasinha ら、2015)。
彗星のスペクトルrH≲2 au は、核とコマの塵から散乱された太陽光による連続光と、ガスコマ内の分子からの共鳴蛍光発光の両方から構成されます。彗星分子の光破壊寿命は、rH2 C/2024 S1のような太陽近傍の彗星では非常に短い。さらに、彗星種(例えばCN、C 2、C 3)からのガス放出帯は、短い可視波長に集中している(Herzberg、1950)であり、主に B および V 広帯域フィルターを汚染します。ここでは、放射の大部分が彗星の塵から散乱した太陽光であると想定して、R フィルターの光度測定のみを分析します。
絶対等級は、彗星の等級を
rH=Δ= 1 au およびα= 0°。固定線状開口測光の場合、見かけの等級と次の式で関係する。

どこΦ(α)位相角に対応する位相関数である
α(正規化してΦ(0)=1)。NOT観測の位相角は比較的大きく(51°~65°:表1)、(測定されていない)位相関数を考慮する必要がある。便宜上、Schleicher 1による表を使用したが、結果はMarcus(1986幸運なことに、角度依存性が最も強く、不確実性が最も大きいのは
Φ(α)前方散乱ジオメトリに限定される(α≳120°)と感度α
NOTデータの範囲は控えめです。例えば、シュライヒャー曲線は、Φ(50°)= 0.38からΦ(90°)= 0.54。それでも、S1 の位相関数は測定されたものではなく仮定された量であることに留意し、2 倍の誤差が生じる可能性が十分にあると予想します。
図3は絶対等級ではないことを示しています。等級の変化は、彗星の場合に広く行われているように、太陽中心からの距離の単純なべき乗関数では表すことができません。代わりに、H最初は各開口部がフェードインし、〜10月3日(rH10月11日(0.725 au)まで減少したが、10月17日(0.544 au)までに減少に転じ、〜
10月19日までに3.5等級(0.476 au)まで明るさが上昇する。
Δ(5−10)=R5−R10、 そしてΔ(10−15)=R10−R15そしてΔ(5−15)=R5−R15
は、核からの距離の関数として測定されたコマ表面輝度の急峻さの大まかな尺度を提供し、値が小さいほど表面輝度プロファイルが急峻であることを示します。図3 は、10月17日と 19日に 3 つの差がすべて縮小していることを示しています。これは、核からの新鮮な物質の放出によって表面輝度プロファイルが急峻になっていることと一致しています。
彗星のRバンド絶対等級は散乱断面積と関係があり、Cによる

どこPR Rバンドの幾何アルベドであり、Hは絶対等級である。S1の幾何学的アルベドは測定されていないので、
pR= 0.04であり、他の彗星と同等である。
メートルR、Hおよび断面C表3にまとめました。
表3の大きく変化する断面積は、核ではなくコマ内の彗星塵による散乱を反映している。近日点前核の最も厳しい制限は、最小の断面積によって設定される。
C5= 17 km^2、UT 2024年10月11日に測定。等面積円の半径はrn=(C5/π)1/2〜2.3 km は、測光における塵の混入により、核の近日点前半径に強い上限を設定します。
近日点通過前の核半径にもっと厳しい制限を課すために、10月11日の破片測光を調べました(図2)。この日、彗星は少なくとも4つの別個の源をダストテールに埋め込んでいます。これらのうち最も東にある成分Aが主核で、他の源はガス放出力によって太陽から押しのけられた破片であると想定しています。成分Bが成分Aよりも明るいのは驚くことではありません。なぜなら、各成分の明るさはダストからの散乱によって支配されているからです。半径5ピクセル(1.1インチ)の絞りを使用すると、成分Aの見かけの等級は次のようになります。
m5= 19.0、絶対等級H5= 18.4。これらの数値の不確実性は、主に系統的誤差(例えば、小さな開口部や測定されていない位相関数によって引き起こされる)によって決まります。式2の断面積はC= 1.1 km^2、半径の円の面積に等しいrn= 600 m。厳密に言えば、コンポーネント A は明らかに非恒星であるため、これは依然として核の半径の上限です。
UT 2024 11月6日と10日に、近日点通過後に残っている可能性のあるS1の残骸を探すために、追加のNOT画像を取得しました。薄暮時に撮影された画像には、点光源の等級制限があり、彗星の兆候は見られません。
11月6日にmR>18.2、11月10日のmR>19.5。この日のエフェメリス精度(JPL Horizonsより)は1σ〜±12インチは、6.5フィートのALFOSC視野に比べて小さいため、指向性は問題にならないはずです。生き残った核のサイズを制限するために、C型小惑星位相関数を想定しました。これは、−2.5log10 (Φ(α))= この2つの日付で2.6等級と2.5等級(表1参照)α= 0°。近日点後の核の絶対等級の限界は
HR>17.2 およびHR>11月6日と10日のUTではそれぞれ18.1である。11月10日のより厳しい観測値を用いると、式2は散乱断面積の限界を与える。
C<1.4 km ^2(球半径に相当)
rn<核半径の限界は、近日点通過前の測光から決定された半径の限界と本質的に同じです。したがって、近日点通過後のデータから核が破壊されたと結論付けることはできませんが、核が検出されなかったことは、この可能性と一致しています。
STEREO COR-2Aデータ: NOTのデータに加えて、NASAの太陽観測衛星STEREO-A ( Howard et al. (2008)、Eyles et al. (2009))。我々は、外部から遮蔽されたLyotコロナグラフであるCOR-2Aカメラのデータを使用した。これは、〜2~15 R ⊙。COR-2Aカメラの画像スケールは14.7″ピクセル-1(つまり、各ピクセルは立体角を占める)です。〜ALFOSCデータよりも4700倍大きい)と有効波長〜7000Å、1000Å幅のバンドパス。Cor-2Aの画像は、強力で高度に構造化された可変的なコロナ背景の影響を受けています。コロナを抑制するために、まず10月27日から28日に撮影された114枚のCOR-2A画像から各ピクセルの最小輝度値を見つけ、この画像を個々の画像から減算しました。次に、6秒間積分したCOR-2A画像を通常5枚から6枚の画像の中央グループに結合し、より優れた信号対雑音比のデータを提供しました。画像の位置合わせは、フィールドの星とS1のJPL Horizonsエフェメリスを使用して行いました。また、測光較正のために、彗星データと同じ方法で処理されたフィールドの星の恒星位置合わせされた合成画像を使用しました。彗星は10月27日にCOR-2Aフィールドに入り、約24時間見え続けました。STEREO-A観測の記録を表2に示し、結合した画像を図4に示します。
宇宙望遠鏡から彗星までの距離は、〜STEREO-A観測が行われた1日間。そのため、固定角度半径5ピクセルと10ピクセル(74″と147″)の円形投影アパーチャを使用し、外半径50ピクセル(735″)の連続した環状部内で計算された中央信号からの背景減算を行った。5ピクセルと10ピクセルのアパーチャ半径は、彗星でそれぞれ48,000 kmと96,000 kmに相当する。これらのアパーチャからの等級を次のように呼ぶ。
R48そしてR96天空開口部の中央信号の使用により、彗星の尾からの光が適切に除去され、残留コロナ背景が適切に表現されていることを確認しました。
測光は5ピクセルと10ピクセルの開口部内の絶対等級を見つけるために補正されました。
H48そしてH96、それぞれ上記の通り(表4)。図5は、彗星が約rH= 0.075 au (16 R ⊙ )。その後、約2等級ずつ減光し、最後に検出されたのは
rH= 0.019 au (4.1 R ⊙ )、近日点の 0.008 au (1.7 R ⊙ ) のわずか 2.3 時間前です。
また、近日点通過後のCOR-2A画像合成も調べ、S1の残存物を探しました。UT2024年10月29日02時53分までに取得された画像(rH= 0.074 au または 16 R ⊙)は S1 の証拠を示さず、その後、彗星の天体位置はコロナグラフの視野外になりました。
3議論
NOTとSTEREO-Aの観測結果から、
1) 近日点通過前の絶対等級は10月3日から10月11日までの期間のNOTデータで大きく変化した(rH= 0.937 au から 0.460 au までの範囲で変化しましたが、単純なべき乗則型の依存性はなく、最初は暗くなり、その後突然明るくなりました。
2) 10月11日に撮影された破片(rH= 0.725 au; 図2 ) は、核が近日点よりずっと前に崩壊していたことを示しています。
3) 近日点前核半径はrn= 600 m (アルベド 0.04 と仮定)
4) STEREO-Aデータにおける絶対輝度のピークは10月27日で、
rH= 0.075 au (〜16 R ⊙)。その後、彗星は10月28日の最後の近日点通過前観測まで暗くなり、rH= 0.02 au (4.1 R ⊙ )。
5) 彗星は近日点通過後にはSTEREO A観測でも、より感度の高いNOT地上データでも検出されなかった(表1)。近日点通過後のNOTデータから、残存するコンパクト核の大きさに上限が示された。rn≤700 m(アルベド0.04と仮定)。
3.1物理的プロセス
C/2024 S1 の外観と測光の変化に影響を与える可能性のある物理プロセスについて簡単に考察します。
岩石の昇華:球状の等温黒体の平衡温度は、
TBB=278rH^−1/2は、図5の上軸に沿って示されています。S1彗星は、rH〜0.075 au (16 R ⊙ )、これはTBB〜1000 K です。小さな粒子 (黒体ピークの波長よりも半径が小さい粒子) は、放射率が低いため、さらに高い平衡温度まで上昇します。1000 K を超える温度は、露出した水氷が生き残るには高すぎますが、より耐火性の高い物質の昇華と一致します。例として、オリビンは彗星のコマに豊富に存在することが知られています(Zolensky ら、2024)であり、オリビンの昇華距離は0.07 au(〜15 R ⊙ ) (小林ら、2011)は、明るさのピークの位置と非常によく似ている。オリビンまたは同様の昇華潜熱を持つ他の物質のコマ粒子の昇華は、図5に見られるS1の近日点付近での減衰を説明する可能性が高い。太陽に接近する彗星は、一般的に、近日点付近で見かけの等級が最大になる。
〜10~14 R ⊙ (ナイトら、2010これは核の完全な溶解を表すと解釈されてきたが、コマ粒子の昇華は、追加の、そして確かに避けられない説明を提供する。
β流星体は、太陽から10~20 R ⊙ の距離にある黄道塵粒子の昇華によって発生します(Szalay et al.、2021)。
S1の核にはほんのわずかな部分しか存在しないことに注意することが重要です(≲全体の(コマが支配的な)散乱断面積の 0.1% です。したがって、彗星の近日点付近での減衰から核が破壊されたと結論付けることはできませんが、その可能性を否定することもできません。
伝導:熱伝導はS1の核の破壊には重要ではない。これを確認するには、経過時間に注目してください。
τ熱は距離を越えて伝導する d〜(κτ)^1/2、伝導前面の有効速度は、Vc=d/τは次のように与えられる。
Vc〜(κ/τ)^1/2。 ここ、κは熱拡散率であり、彗星に見られる多孔質物質の場合、値は
κ〜10^−9m^ 2 s^ -1。τ〜150日(1.3×10^7 3 auの水の昇華線を通過する時点と近日点の間の距離を計算すると、
d〜0.1 m、平均伝導前線速度はヴc〜8×10^−9ms^ -1。このように薄い表面層から氷が失われても、核全体の安定性や存続には何の影響も及ぼさない可能性がある。
氷の昇華: S1からの質量損失は、昇華による表面のアブレーションによって支配される。
rH≲1 auの場合、太陽に垂直に露出した完全に吸収する平坦な水氷表面からの平衡昇華率は、エネルギーバランスによって次のように表される。

どこL⊙= 4×10^26Wは太陽の光度、rHは太陽中心からの距離であり、H=2.8×10^6J kg -1は昇華潜熱である。例えば、距離が
rH= 1.0 au(表1参照)、式3はfs〜0.5×10^−3kg m -2 s -1。かさ密度は
ρ= 500 kg m^ -3 ( Groussinらによる彗星核の公称密度(2019) 、氷の表面が昇華によって後退する速度、
Vs=fs/ρ、 はどこL⊙= 4×10^26Wは太陽の光度、rHは太陽中心からの距離であり、H=2.8×10^6J kg^ -1は昇華潜熱である。例えば、距離が
rH= 1.0 au(表1参照)、式3はfs〜0.5×10^−3kg m^ -2 s^ -1。かさ密度はρ= 500 kg m^ -3 ( Groussinらによる彗星核の公称密度(2019) 、氷の表面が昇華によって後退する速度、Vs=fs/ρ、 はVs〜1×10^−6ms^−1、伝導前線の速度よりも約2桁速い。このため、S1の表面の氷からの昇華により、下から冷たい氷が継続的に露出することになる。
これをさらに詳しく調べるために、S1が太陽中心から遠距離から近日点まで移動する際の累積的な氷の損失を計算した。Vs〜1×10^−6ms^−1、伝導前線の速度よりも約2桁速い。このため、S1の表面の氷からの昇華により、下から冷たい氷が継続的に露出することになる。
これをさらに詳しく調べるために、S1が太陽中心から遠距離から近日点まで移動する際の累積的な氷の損失を計算した。

どこΔZ(rH)遠日点から遠距離に移動する際に失われる氷層の厚さですrH、t0遠日点における時間であり、t彗星が到達した時間です
rH我々は、rHそしてtケプラー方程式の数値解法と計算によってfs昇華平衡方程式から

どこAそしてϵ氷のボンドアルベドと赤外線放射率です。Aまたはϵは知られているが、その影響はfs無視できるほど小さいA≪1とϵ〜1. 私たちは仮定した
A= 0 かつϵ= 1. エネルギーバランス計算には幾何学的補正を含めました。γ(rH)= 1−(r⊙/rH)^2太陽の半球全体がS1から見えないという事実を説明するために、rH/R⊙小さい。(この幾何学的補正は周辺減光の影響を無視しており、rH/r⊙→1なので、概算値として考えなければならない。しかし、ΔZいずれにしても、彗星が太陽に接近する時間は非常に短いので、この値は小さい。シュテファン・ボルツマン定数はσ=5.67×10^−8W m^ -2 K^ -4 . 数量χは、核表面上の熱の空間分布を反映する無次元パラメータである。太陽-彗星線に垂直な平面の場合、
χ= 1 一方、昼側のみ加熱された球状核の場合、χ= 2であり、等温球の場合は、χ= 4. 彗星は主に太陽に面した熱い側から昇華することが知られているので、後者の制限は無視し、χ= 1 と 2。
式5は水氷の質量昇華フラックスについて反復的に解かれた。fs(rH)図6にプロットされた結果は、2つの照明ケースを示しています。青い実線は、
χ= 1。与えられた条件における最大可能温度と昇華速度を表す。rHは、S1の太陽直下の点の高温にほぼ相当する。破線の赤い曲線は、χ= 2。
曲線は類似しており、式3に基づく推定と一致している。図6は、遠日点から1 auまでの氷の累積損失がΔZ〜数メートル、近日点まで延長すると損失が近づく
ΔZ〜50 mから100 m。近日点に向かう途中での抑制されない昇華は、半径50 mから100 m未満の核を破壊する可能性があり、これは、一般的に小さいクロイツ彗星のほとんどの消滅のもっともらしい(ただし、唯一の原因ではない - 以下を参照)原因である(ナイトら、2010)の計算では
Δず明らかに理想化されていますが、近日点距離が小さいことによる熱の影響が大きいことを示しています。
回転不安定性:昇華する核からの異方的な質量損失は、回転を変えるトルクを及ぼします。十分な時間が与えられると、このトルクは回転を不安定な点まで加速させます。短周期彗星の最近の測定では、流出運動量は主に核の半径方向ですが、中央値の割合、
KT〜0.7%、核を回転させる(Jewitt、2021)。核を初期半径の球体とみなすと、rn、 密度ρ、角周波数で回転するωスピン角運動量は次のように表される。L=(2/5)Mnrn^2ω、 どこMn=4πρrn^3/3は核質量であり、

厚さの殻の質量ΔrはΔm=4πrn^2ρΔr、その直線運動量は、速度で放出されたときⅤthはΔmⅤth
そして、殻の放出による角運動量の変化はΔL=ΔmVthKTrn、 または

設定
ΔL=Lを表す式を与える
Δr、原子核の角運動量を大幅に変化させるために失われなければならない殻の厚さ、

評価する
Δr私たちは設定しました
rn= 600 m、近日点前測光法で許容される最大値。コマ膨張速度は
rH= 1 auとしてⅤth〜500 ms^ -1、これは300 Kの水分子の熱速度に等しい。S1の核の角周波数は不明だが、ほとんどの彗星核の自転周期は2倍以内である。
〜10時間(ω〜1.7×10^−4s^ -1 ) (ココタネコバら、2017)を代入すると、半径600mの核はわずか1層しか昇華する必要がないことがわかります。
Δr= 2.3 mの厚さで、回転を2倍に変化させます。図6は、太陽中心からの距離が2.3 mに達する累積昇華損失を示しています。
rH= 0.5 auから1.1 au(表面温度の空間分布に依存する)であり、
〜0.7 auの距離で、S1は初めて断片化した外観(図2)と劇的な明るさの急増(図3)を示しました。これは、核がこれらの近日点前距離で回転不安定性に達したことの証拠ではありませんが、核が構造的に凝集していないと仮定すると、この推論は確かにもっともらしいものです。
式8は、Δrスケールはrn^2そのため、核の半径が600メートルより小さければ、さらに薄い表面層の放出によるトルクが核を回転させるのに十分なものとなり、さらに大きな太陽中心距離でも崩壊が始まる可能性がある。ほとんどのクロイツ彗星は小さい(数個から〜50mの物体は近日点まで生存できない。式8に従うと、50mの物体は〜2cmの氷の損失は、ガス放出トルクによってその回転が実質的に変化するには十分である。図6は、小惑星帯の距離でも2cmの氷の損失が起こり得ることを示し、ほとんどの小さなクロイツ彗星が発見されるずっと前から崩壊が始まっている可能性があることを示唆している。急速な自転が主に
<100 m の物体(Warner et al.,2009)、回転崩壊に対する生存は有限の凝集強度の役割を反映している可能性がある。
一方、式8は、非常に大きなクロイツ彗星の核は、近日点に向かう途中で昇華する機会が限られているため、回転による崩壊に耐えられるはずであることを示している。
Δr= 50 mから100 m(近日点までの最大累積昇華損失、図6を参照)を式8に代入し、他のパラメータは上記と同じとすると、近日点に向かう途中で回転できる最大の核の半径は次のように表される。
rn= 2.8 kmから3.9 km。残念ながら、最大のクロイツ彗星核の大きさは観測的によく決定されていません。サングレーザーC/2011 W3(ラブジョイ)は近日点近くで崩壊したようです。その核の大きさは不確かですが、ほぼ確実に1 km未満でした(レイモンドら、2018ナイトら(2010)の表1には、近日点通過後の彗星C/1965 S1(池谷・関)の半径(これも非常に不確か)が4.3キロメートルと記載されている。大きなクロイツ彗星は、C/1965 S1 (セカニナ、1966)ですが、回転バーストによって破壊される可能性は低いです。
これらの考察は明らかに非常に粗雑である。核は球形ではない可能性があり、質量は表面殻から均一に失われる可能性は低く、
KT短周期彗星で測定された(Jewitt、2021) はS1 には当てはまらない可能性があり、構造的には弱いものの、回転による破裂に抵抗するのに十分な強度がある可能性がある。とはいえ、ガス放出トルクによるスピンアップは、この彗星や他の 1 キロメートル未満の太陽接近彗星の分裂のもっともらしい原因であり、核破壊への素早い道筋となる。核を分裂に向かわせるには表面が数メートル失われるだけでよいため、回転破壊は核破壊につながる最も効率的な経路である。
ロッシュ不安定性: 太陽の重力の核直径にわたる勾配は、ロッシュ距離内での混乱の潜在的な原因である。

どこΓは無次元定数であり、ρ⊙= 1300 kg m^-3は太陽の密度です。強度のない球体の場合、Γ〜2.4、そして
ρ= 500 kg m^-3式9はrR/R⊙〜3.3. これは近似値に過ぎない。なぜなら、原子核は強度がないか球状である可能性は低く、また式9では原子核の回転による不安定化の影響も無視しているからである。不安定距離はこれよりも大きいか小さいかのどちらかである。
rR/R⊙〜3.3 潮汐力の強さ、形状、回転によって変動します。しかし、近日点付近(rH/R⊙〜1.7)は、木星のロッシュ球に入ったときに分裂した彗星D / 1993 F2(シューメーカー-レヴィ9)の場合と同様に、S1の見かけ上の消滅に寄与した可能性が高い(Asphaug&Benz、1996)、そしてC/1965 S1(池谷・関)は、0.008 au近日点(セカニナ、1966)。
S1彗星は、発見されるほど明るかったという点で珍しい。
〜1 auであるのに対し、クロイツ彗星のほとんどは小さすぎる(半径数auから〜50 m (ナイトら、2010) ) であり、この距離では検出できないほど暗い。S1の早期検出は、その核が平均よりも大きいことを示唆しており、経験的な上限は
rn<600m。さらに大きなクロイツ彗星もいくつか知られている。例えば、C/2012 S1(ISON)の核は600m≤rn≤900 m (Lamy et al.,2014)とやや大きい。
そして最も有名なクロイツ彗星であるC/1965 S1(池谷・関)はおそらく
この彗星の核の大きさに関する信頼できる推定値は存在しないが、半径は>1 kmである。ほとんどのクロイツ彗星は近日点前か近日点近くで消滅し、C/2024 S1やC/2012 S1(ISON)も同様である(Keane et al.、2016回転とアブレーションによる破壊を生き延びるのに十分な大きさの太陽接近型天体だけが、太陽のロッシュ球に入ると、重力による破壊の最後の試練(式9)に直面する。
4まとめ
地上および宇宙望遠鏡によるクロイツ彗星C/2024 S1の光学観測では、
1. 近日点前核半径はrn<600 m (赤色幾何反射率 0.04、C 型位相関数を想定)。近日点前 0.7 au までに核の複数の成分への崩壊が進行していた。
2. 地上で行われた幾何学補正測光では、太陽中心からの距離に単純に依存せず、彗星は最初は〜0.9 au から 0.7 au にかけて 1 等級明るくなり、その後 0.45 au に向かって 3.5 等級明るくなり、非平衡質量損失を示しています。
3. STEREO-Aによる太陽近傍の測光によると、S1は0.075 au付近でピーク輝度に達し、放射温度は〜1000 K で、近日点に向かう途中で暗くなっていった。粒子の昇華がこの近日点付近での暗化を説明できるかもしれない。
4. ガス放出トルクによって引き起こされる回転不安定性は、この彗星や他のクロイツ彗星の太陽に接近する最も効率的な破壊メカニズムであり、次に昇華によるアブレーション損失が続く。近日点に向かう途中で回転破壊とアブレーションを生き延びた核破片は、太陽のロッシュ球に入ると破壊されたであろう。

図 1.— 3 日間の NOT 画像から得た C/2024 S1 の近日点通過前の外観。スケール バーと方向矢印は 6 つのパネルすべてに共通です。

図 2.— UT 2024
10 月 11 日、rH = 0.725 au における C/2024 S1 の近日点通過前の外観を示す NOT 画像。上部の画像は、60 秒積分の各 5 枚の画像の中央値からコンパイルされた生データを示しています。この画像のガウス平滑化バージョンが中央のパネルに表示され、差分画像が下部に表示されます。4 つの個別のオブジェクトにラベルが付けられています。スケール バーと基本方向がマークされています。

図 3.— 近日点通過前 NOT 観測の絶対等級と太陽中心距離の関係。固定投影半径 5,000 km (黄色のダイヤモンド)、10,000 km (赤い四角)、15,000 km (緑の円) の円形開口部内で測定。

図 4.— Cor-2A 合成画像。各パネルは上が北、左が東で、幅は約 1◦ (彗星の位置で 2.4×10^6 km) です。0.039 au および 0.047 au パネルの黄色の目盛りは、近日点通過後の彗星の予想される位置を示していますが、この距離では観測されていません。

図 5.— 太陽中心からの距離の関数としての COR-2A データからの測光値。
絶対等級は、半径 48,000 km (青いダイヤモンド) と 96,000 km (赤い円) の開口部内に表示されます。等温球状黒体温度は、上軸に沿ってマークされています。垂直の破線は近日点を示しています。

図 6.— 2 つの昇華モデルにおける、太陽中心からの距離が減少するにつれて増加する累積氷の融解 (青の実線) 太陽-彗星線に垂直に向いたスラブと、(赤の破線) 太陽に面した半球からのみ昇華する球状の氷表面。
C/2024 S1 の軌道と氷の密度 ρ = 500 kg m^−3 と仮定。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます