光度曲線とカイパーベルトの接触連星の流行の統計上のレビュー

この論文が正しければ光度曲線を分析すればカイパーベルト天体がアロコスみたいな接触連星なのか近接連星なのか判別出来るようです。以下、機械翻訳。
光度曲線とカイパーベルトの接触連星の流行の統計上のレビュー
要約
我々は、それらの光度曲線の統計上の特性を調査することによって、遠いカイパーベルトオブジェクト（KBOs）の人口について学ばれることができるものを調査します。 他の人たちが成功裏に個別の、大いに可変的な KBOs の特性を推論したのに対して、我々は KBOs の分数が低い振幅で同じく人口についての基本的なインフォメーションを提供することを示します。 それぞれの光度曲線が主に２つの要因の結果です：形とオリエンテーション。 我々は、平らになることでそしてなしで、接触連星と 楕円体 の形を考慮に入れます。 数学的なフレームワークを展開した後で、我々はそれを KBO ライトカーブデータの既存のグループに適用します。 主要な結論は次の通りです。（１）絶対等級Ｈを KBOs の大きさの委任状として使うとき、平均よりむしろ光度曲線の最大限（最低Ｈ）を使うことはいっそう正確である. （２）前の調査者がより小さい KBOs がより高い振幅の光度曲線を持つ傾向があることを指摘して、そしてこれをそれらが好調でより大きい KBOs よりシステマティックにいっそう不規則であるという証拠と解釈しました； 我々は大きさから独立している同一の大きさを持っている平らになった死体の住民が同じくこの結果を説明することができたことを示します。 （３）我々の分析の方法はカイパーベルトでの接触連星の割合の事前の査定が人工的に低いかもしれないことを示します。 （４）若干の KBOs の棒方向は数十年のタイムスケールのそれらの光度曲線の観察された変化から推定されることができます；しかしながら、我々はこれらの KBOs がその棒オリエンテーションが全体的に住民の代表者でない偏ったサンプルを構成することを示します。 （５）表面地形、 albedo パターン、濃くなっている手足と他の表面の敷地が個別の光度曲線に影響を与えることができるけれども、それらは全体的に統計に強い影響を与えません。 （６）太陽系外縁部 Origins 調査（OSSOS）調査からの測光学は前の結果と不適合です、そしてその統計上の不動産は容易な解釈を拒絶します。 我々は来たるヴェラ・Ｃ・ルービン観測所から同じく期待されたもののような未来の、ずっとより大きいデータセットの分析に対するこのアプローチの約束を論じます。
キーワード
カイパーベルト； 海王星以遠天体；測光学；自転の力学

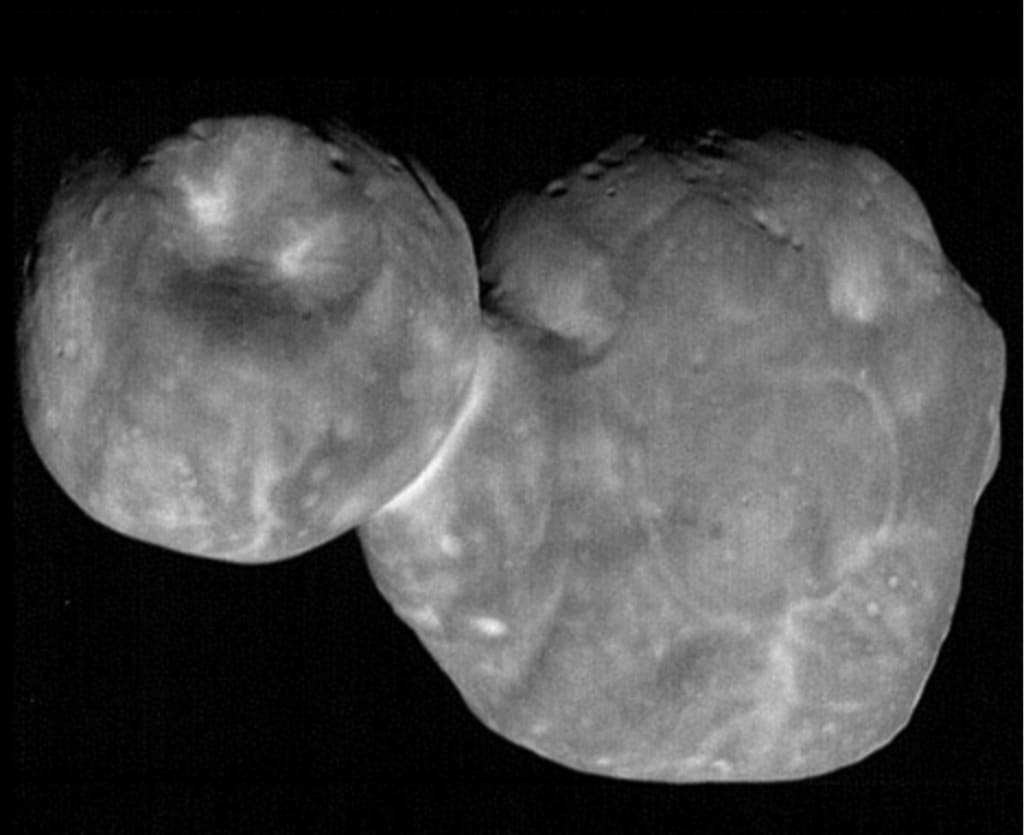
図１。 アロコス 、探査機ニューホライズンズ によって映し出されるように、冷たい古典的な接触連星のアロコス。 長い軸は約３６キロです（スペンサーおよびその他、２０２０；スターンおよびその他、２０１９）。


図2. 2つの理想的な形状のシミュレートされた回転光度曲線。
接触連星と楕円体。 接触している2つの等しい球からなる物体（a）は、深くて狭いことを示しています
明るさの最小値とより広い最大値。 2：1：1の楕円体（b）は、より正弦波の光度曲線を示しています
本来は。 各曲線は、極の異なる方向に対する360°の回転を含みます：ϕ = 0°
は回転極に沿ったビューに対応しますが、ϕ = 90°は極に垂直なビューの場合です。
点線は、ϕの15°ステップでの中間光度曲線を示しています。 挿入図は各形状を示しています
指定されたϕの値（に向かって回転）に対する最小輝度（θ= 90°）での空の外観
正しい）。 縦軸は光度の単位ですが、値は下向きに増加するため、明るさは
曲線で上向きに増加します。


図3.さまざまなローブサイズの接触連星の光度曲線モデルをそれらと比較します
同等の寸法の楕円体の。 挿入画像は、小さいローブが含まれるバイナリを示しています
大きい方の半径の40％から100％の間の半径を持っています。 （a）これらの回転光度曲線
モデルは、すべてϕ = 90°と仮定して、同等の楕円体のモデルと比較されます。 曲線が繰り返されます
180°ごとですが、両方の極値が見やすいように240°の回転を示しています。 （b）
極の向きに対するピークツーピーク光度曲線振幅Δmの依存性。 ラベル
右側は、接触の大きい球の半径に対する小さい球の半径を示しています
バイナリ。 パネルaのθ= 90°およびパネルbのϕ = 90°付近の平坦な領域は、小さいために発生します。
葉は完全に大きな葉の前または後ろにあります。


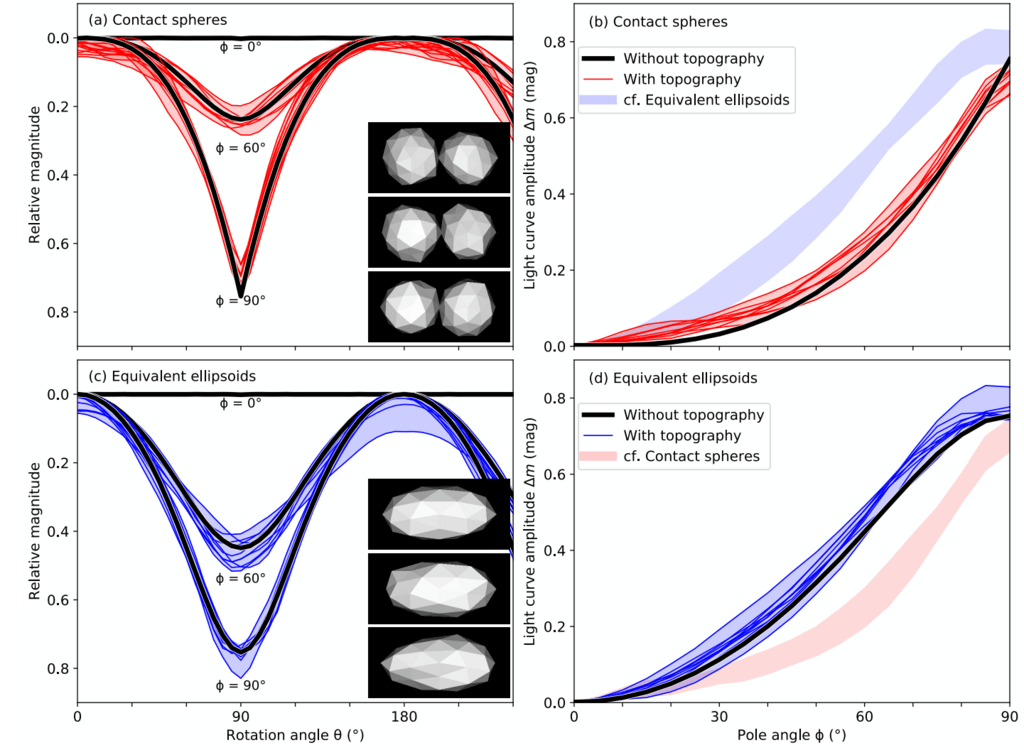
図4.不規則な形状の影響のシミュレーション。元の体型は球に触れていました
同じサイズ（パネルa、b）と2：1：1の楕円体（c、d）。左側のパネルは、極の回転光度曲線を示しています
0°、60°、および90°の角度ϕ;パターンは180°ごとに繰り返されますが、240°の回転を示しているため、
光度曲線のピークは簡単に調べることができます。右のパネルは、光度曲線の振幅Δm対ϕを示しています。挿入図
画像は各形状の3つの例を示しています。各パネルで、細い線は10個のランダムな結果を示しています
各形状モデルの実現、および光の陰影は、極値の間のゾーンを塗りつぶします。ヘビー
線は、元の歪みのない形状のモデリング結果を示しています（図3を参照）。パネルdの影付きゾーンは
パネルbで複製され、その逆も同様です。これにより、2セットのモデルを簡単に比較できます。ほとんどの場合、
形状の不規則性により、光度曲線が0.1等未満変化します。振幅Δmはほとんどの下で増加します
状況は異なりますが、特定の形状や向きでは減少する場合があります。


図5.球に触れる場合のアルベドパターンの効果のシミュレーション（パネルa、b）および2：1：1
楕円体（c、d）。 各ボディの表面は、ランダムに配置された三角形に分割されています
0.5〜1の割り当てられたアルベド値。左側のパネルは、極角ϕの回転光度曲線を示しています。
0°、60°、および90°; 右のパネルは、光度曲線の振幅Δm対ϕを示しています。 挿入画像は、次の3つの例を示しています。
各アルベドパターン。 各パネルの細い線は、各パターンの10個のランダムな実現の結果を示しています。
ライトシェーディングは、極値の間のゾーンを塗りつぶします。 太線はのモデリング結果を示しています
オリジナルの一定アルベドモデル（図3を参照）。 パネルdの影付きのゾーンは、パネルbに複製され、
逆に、2セットのモデルを簡単に比較できるようにします。 これらのアルベドパターンは増加する傾向があります
Δm、ただし一般的には<0.1等。


図6.周縁減光の影響のシミュレーション。 ボディの光度曲線モデルを比較します
表面は、Lommel-Seeligerの法則に従うものに対してLambertの法則に従います。 私たちのモデルはに基づいています
同じサイズの接触球（パネルa、b）と2：1：1の楕円体（c、d）。 左側のパネルは回転ライトを示しています
15°刻みの極角ϕの値の曲線。 右側のパネルは、光度曲線間の関係を示しています
振幅Δmおよびϕ。 パネルdの影付きのゾーンは、パネルbで複製され、その逆も同様です。
2セットのモデルを比較する方が簡単です。


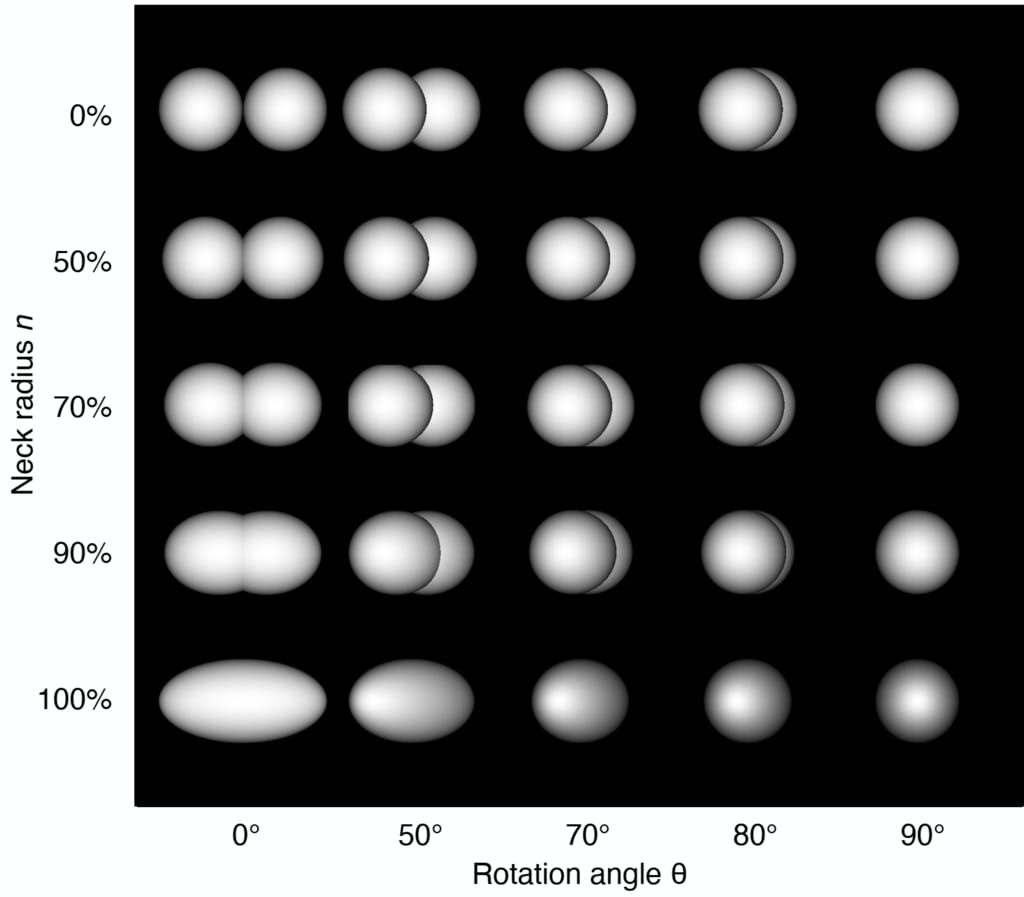
図7.首の役割を示すシミュレーション画像。 首の半径は左側で識別されます。ここで、0％
2つの接触する球を定義し、100％は楕円体を定義します。 視点は垂直です
回転軸（ϕ = 90°）。 回転角は下部に示されています。ここで、ショートに沿ったビューの場合、θ= 0°です。
軸および長軸に沿ったビューの場合はθ= 90°。 これらの図は、ネックの半径がどの程度あるかを示しています。
≤90％は、楕円体よりも球に触れることとの類似度が高くなります。


図8.光度曲線モデルの首の半径への依存性。 （a）極での回転光度曲線
ダッシュパターンで識別される、さまざまなネック半径の角度ϕ = 0°、50°、および90°。 影付きのゾーン
ϕの同じ値の曲線のセットを識別します。 （b）ϕの関数としての光度曲線の振幅。 はめ込み画像
首の半径が100％（楕円体）、90％、70％、50％、および0％（接触球）のモデルを示します。 ご了承ください
50％と70％の首の半径は、接触球の光度曲線に非常によく似た光度曲線を生成します。
楕円体のもの。


図9.光度曲線モデルの平坦化への依存性。 左側のパネルは、極の回転光度曲線を示しています
角度ϕ = 0°、60°、80°、および90°、および比率c / bの4つの値。 行のダッシュパターンは、
比。 挿入図は、側面から見た各サンプルボディの画像であり、最長と最短を示しています。
寸法。 影付きのゾーンは、同じ値のϕを使用して曲線のセットを識別し、マークされたものを示しています
極角の中間値の比率が減少するにつれて、振幅が減少します。 右のパネルは
Δmのϕへの依存性。 パネルdの影付きのゾーンは、パネルbで複製され、その逆も同様です。
2セットのモデルを比較する方が簡単です。 重なり合う領域は、平坦化された楕円体が
平坦化されていない接触連星と同様の動作をします。