潮汐 - 地震共鳴による周回する衛星のその親の惑星への急速な落下

惑星の自転速度が遅いと潮汐力で公転速度が遅くなって落ちてくる。衛星が惑星の変形させると共振して早く落ちてくる。以下、機械翻訳。
潮汐 - 地震共鳴による周回する衛星のその親の惑星への急速な落下
（2019年1月24日に提出された）
潮汐力は、惑星 - 衛星系の進化において重要な役割を果たしています。衛星の潮汐力はそれが周回している惑星の地震波を励起することができます。潮力 - 地震共振は、潮力周波数が惑星の自由振動周波数と一致するときに予想される。ここで我々は、衛星が惑星に接近しているとき、潮汐 - 地震共鳴が大きな振幅の地震波を引き起こすことができ、それが惑星の形状を変え、そして次に衛星に負のトルクをかけてそれを急速に落下させることができる地球に向かって。我々は、潮汐 - 地震共鳴が惑星の降着過程を加速することができる重要なメカニズムであるかもしれないと仮定する。他方で、潮汐 - 地震共鳴効果はまた、衛星の軌道変化の長期追跡によって惑星内部を調べるために使用することができる。
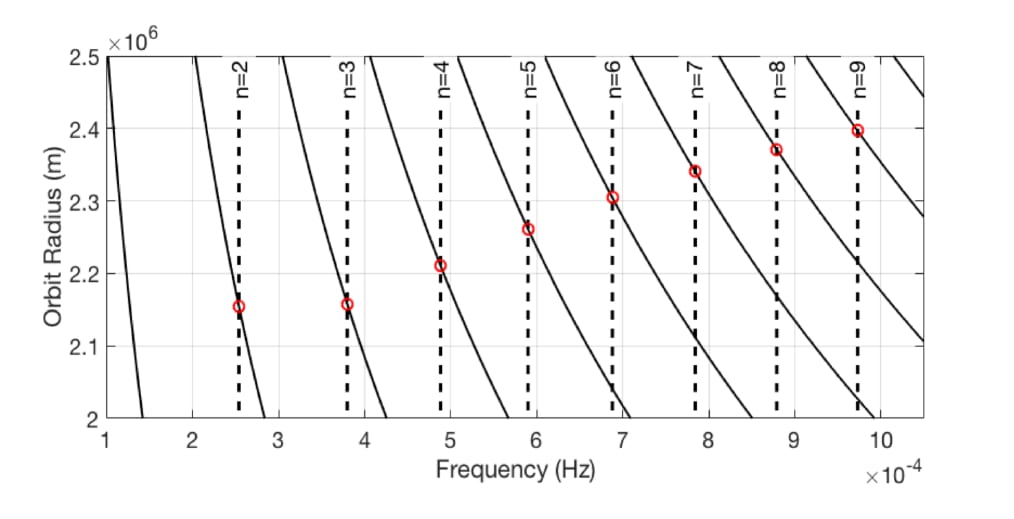
図1.モデル1の潮力と惑星基準モード周波数実線は潮力です
惑星の赤道上の場所で計算された周波数。垂直の破線は、回転楕円体の標準モードの惑星の自由振動周波数です（n = 2、3、4…）。震動共鳴
潮力の周波数が赤い円で惑星の自由振動周波数と交差するときに発生します。


図2.異なる軌道半径で異なるQ値に対して計算された衛星軌道崩壊率
モデル1用。横軸は月の軌道半径です。惑星の半径は
2×103メートル。我々はまた、正弦波共鳴に対して見られると予想される、励起された基準モードをラベル付けする。


図3.惑星の地形モデル（モデル2）。のプロットを誇張しました。
20倍で地形。色は惑星の平均半径に対する地形を示し、
サイズの単位はメートルです。太い赤線は赤道です。青い縦の太い線は
極を通る軸。


図4.軌道半径に対する軌道崩壊率の微分（a）モデル2の場合
地形（b）地形なしのモデル-1の場合。ここで、f @はノーマルモードの周波数です
。破線は軌道周波数がである軌道を示します（nとmは整数です）
破線の隣にラベルを付けます。