
天王星と海王星の経験的構造モデル
2022年1月3日に受領。 2022年2月23日改訂。 2022年3月3日受理
概要
天王星と海王星はまだよくわかっていません。彼らの重力場、自転周期、大気力学、
そして内部構造はよく決定されていません。この論文では、天王星と天王星の経験的構造モデルを提示します。
密度プロファイルがポリトロープで表される海王星。これらのモデルを使用することにより、
惑星重力場、我々は様々な仮定された回転のためのより高次の重力係数J6とJ8を予測します
周期、風の深さ、および低次高調波の不確実性。より速い回転および/または強風であることを示します
中央に集中した密度分布を優先します。 J6またはJ8の正確な決定が
10%以下の相対的な不確実性は、天王星と海王星の風の深さを制限する可能性があります。また、
ボイジャーの自転周期は、天王星と海王星の測定された形状と一致していません。次にデモンストレーションします
重力場のより正確な決定は、内部構造の可能な範囲を大幅に減らすことができます。
最後に、天王星と海王星の慣性モーメントを相対的なもので正確に測定することをお勧めします
〜1%と〜0.1%の不確実性は、それぞれ自転周期と風の深さを制約する可能性があります。
キーワード:惑星と衛星:個人:天王星;惑星と衛星:個人:海王星;惑星と
衛星:インテリア;惑星と衛星:構成

図1.天王星(青色)と海王星のさまざまな惑星モデルのJ6(左パネル)とJ8値(右パネル)の予測
(赤色)。 惑星モデルは、x軸に沿って省略名で収集されます(「U」:ウラヌス、「N」:ネプチューン、「cd」:corr dyn)。
点は平均値を示し、バーは標準偏差を示し、ボックスは完全な解の範囲を示します。
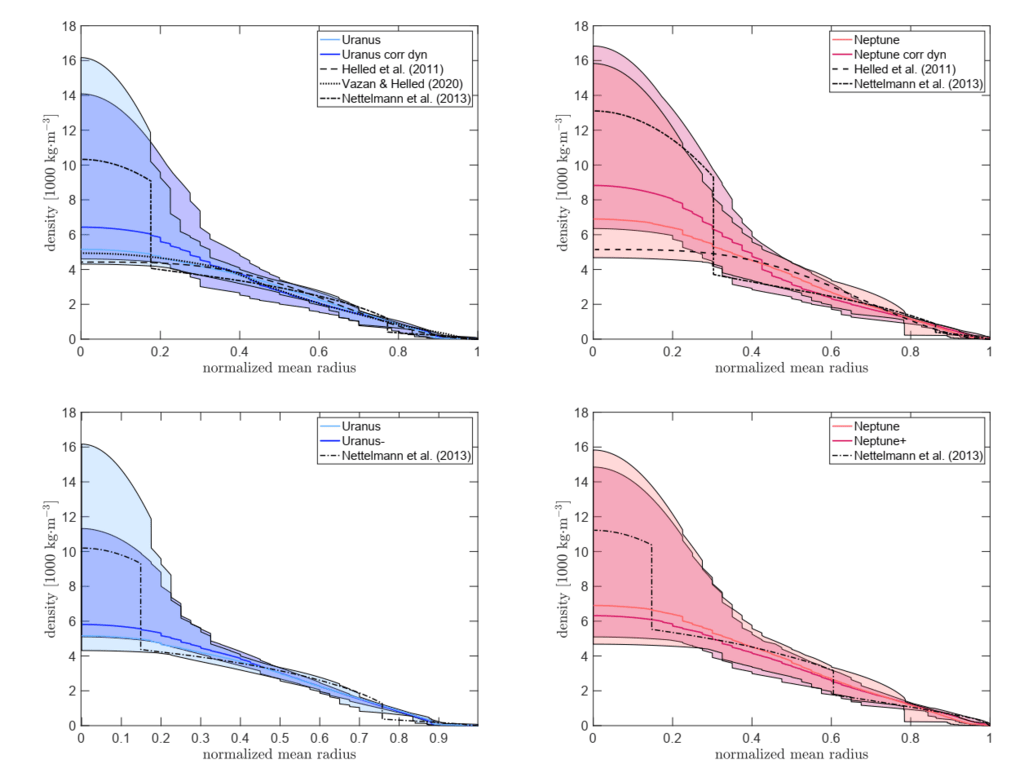
図2.想定される自転周期が異なる天王星(左の列)と海王星(右の列)の推定密度プロファイル
パネル)と風の深さ(上のパネル)。 実線の曲線はサンプルの中央値を表し、影付きの領域は
すべてのソリューションの96%。 上のパネルには、Helledらの天王星と海王星のソリューションが含まれています。 (2011)、Nettelmann etal。 (2013)
およびVazan&Helled(2020)(それぞれ、黒い一点鎖線、一点鎖線、および点線)。 下のパネルには、「天王星」と
Nettelmannらの「Neptune +」密度プロファイル。 (2013)(黒い一点鎖線の曲線)。
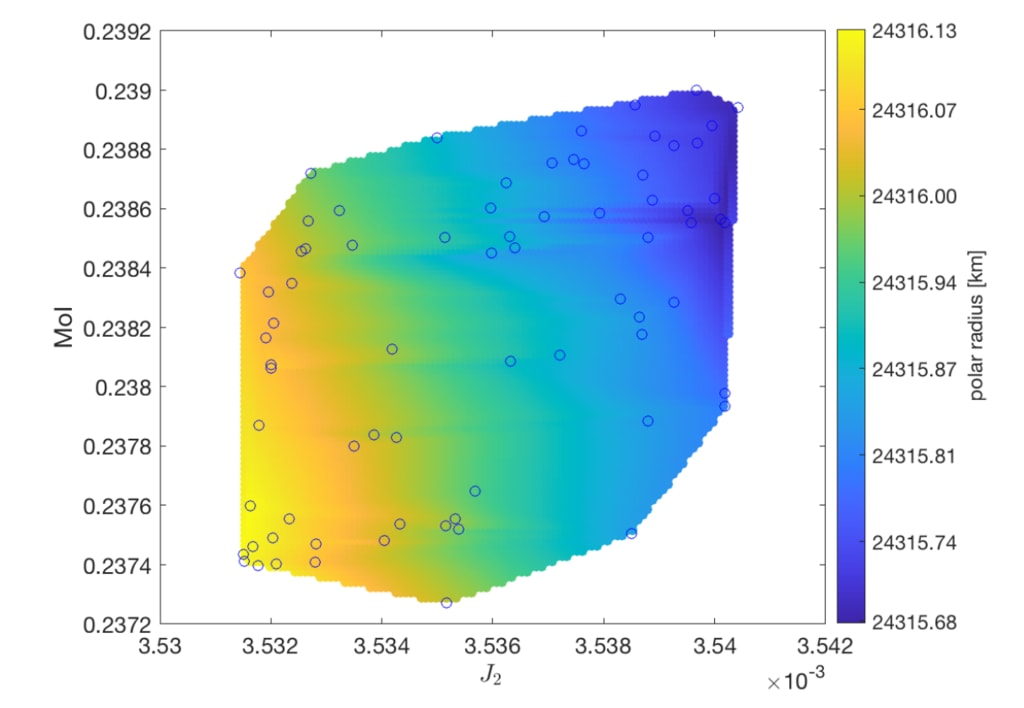
図3.海王星の極半径MoIと
J2。 青い円は良い解決策を示しています。 色はに対応しています
解の間で補間された推定極半径。

図4.極半径と想定されるものとの関係
天王星(ブルーダイヤモンド)と海王星の(均一な)自転周期
(赤い四角)。 破線は最適な曲線を示しています。 The
点線は推定極半径24,973km(天王星)を示しています
と24,341キロ(ネプチューン)。 PVoyに属する自転周期は
黄色の星で強調表示されます。 Helledらの結果。 (2010)
(剛体回転の場合)PHASに基づくものは緑色で表されます
五芒星。
図5.天王星(青色)と海王星(赤色)の推定MoI値。 惑星モデルは、
省略名のx軸(「U」:ウラヌス、「N」:ネプチューン、「cd」:
corr dyn)。 ドットは平均値を示し、標準偏差を示します
ボックスはソリューションの全範囲を示しています。 選択された惑星モデルの場合、黒い水平線はNettelmannのソリューションを表しています。
etal。 (2013)。
4まとめと結論
この作品では、天王星の経験的構造モデルを提示します
密度プロファイルが(up
3)ポリトロープ。これらのモデルを使用して、J6を予測します
とJ8の値と深風の影響を調査し、
推定されたJ6、J8、極半径、MoI、および密度分布の想定回転周期。次に、
J値、惑星の形、および
風の深さ。 J6とJ8を正確に決定することで、風の深さを制限できることを示します。私たち
また、海王星のJ2のより正確な測定値も示しています
J4は、可能なパラメータ空間を大幅に減らすことができます
ソリューションの。天王星の自転周期も示します
とネプチューンは推定値と最も一致しています
極半径。最後に、MoIを正確に測定することで、風の深さをどのように制限できるかを調査します。
天王星と海王星の自転周期。
私たちの主な結果は次のように要約できます。
(i)天王星と海王星のJ6とJ8の予測は、ダイナミクスに強く依存します。正確な測定
J6またはJ8の(数パーセントの相対的な不確実性を伴う)
天王星とネプチューンの風の深さを制限するために必要です。
(ii)天王星の深部内部の密度分布
海王星は自転周期に大きく依存します
ダイナミクスの影響を強く受けます。均一な回転を想定したモデルの場合、風補正を使用することが重要です
重力係数:J
統計2n = Jmeas 2n − Jdyn 2n。
(iii)J2およびJ4のより正確な測定により、さらに
密度分布を制限し、範囲を狭める
天王星のJ6、J8、MoIの予測解のネプチューン。
(iv)天王星と海王星の両方の正確な決定のために
MoIのは、異なるものを区別するために使用できます
自転周期と風の深さを制限します。ために
前者の場合、1%の相対精度が必要ですが、
後者の場合、0.1%の相対精度が必要です。
(v)天王星の一般的に使用される形状と
海王星は、広く使用されている自転周期PVoyとPHASに同意しません。したがって、私たちはその必要性を繰り返します
回転のロバストで独立した測定の
天王星と海王星の時代と形。
将来の作業では、推定された圧力と密度の関係を使用できます
提示された経験的構造モデルを用語で解釈する
構成の。これにより、可能性を探ることができます
天王星と海王星の組成、および識別
組成勾配とそれらの依存性を決定する
想定される自転周期と風の深さ。私たちは
将来の研究でこれに対処します。
最後に、天王星や海王星への専用の宇宙ミッションの必要性を強調します(例:Arridge et al.2014;
マスターズ他2014; Mousis etal。 2018; Hofstadter etal。 2019;
フレッチャー等。 2020)。そのような使命はすべきであると私たちは提案します
惑星の重力場を測定するように設計されている、
J2とJ4の不確実性を減らし、決定する
高階J6とJ8と惑星の形、そして
可能、惑星の自転周期、およびMoI。
2022年1月3日に受領。 2022年2月23日改訂。 2022年3月3日受理
概要
天王星と海王星はまだよくわかっていません。彼らの重力場、自転周期、大気力学、
そして内部構造はよく決定されていません。この論文では、天王星と天王星の経験的構造モデルを提示します。
密度プロファイルがポリトロープで表される海王星。これらのモデルを使用することにより、
惑星重力場、我々は様々な仮定された回転のためのより高次の重力係数J6とJ8を予測します
周期、風の深さ、および低次高調波の不確実性。より速い回転および/または強風であることを示します
中央に集中した密度分布を優先します。 J6またはJ8の正確な決定が
10%以下の相対的な不確実性は、天王星と海王星の風の深さを制限する可能性があります。また、
ボイジャーの自転周期は、天王星と海王星の測定された形状と一致していません。次にデモンストレーションします
重力場のより正確な決定は、内部構造の可能な範囲を大幅に減らすことができます。
最後に、天王星と海王星の慣性モーメントを相対的なもので正確に測定することをお勧めします
〜1%と〜0.1%の不確実性は、それぞれ自転周期と風の深さを制約する可能性があります。
キーワード:惑星と衛星:個人:天王星;惑星と衛星:個人:海王星;惑星と
衛星:インテリア;惑星と衛星:構成

図1.天王星(青色)と海王星のさまざまな惑星モデルのJ6(左パネル)とJ8値(右パネル)の予測
(赤色)。 惑星モデルは、x軸に沿って省略名で収集されます(「U」:ウラヌス、「N」:ネプチューン、「cd」:corr dyn)。
点は平均値を示し、バーは標準偏差を示し、ボックスは完全な解の範囲を示します。

図2.想定される自転周期が異なる天王星(左の列)と海王星(右の列)の推定密度プロファイル
パネル)と風の深さ(上のパネル)。 実線の曲線はサンプルの中央値を表し、影付きの領域は
すべてのソリューションの96%。 上のパネルには、Helledらの天王星と海王星のソリューションが含まれています。 (2011)、Nettelmann etal。 (2013)
およびVazan&Helled(2020)(それぞれ、黒い一点鎖線、一点鎖線、および点線)。 下のパネルには、「天王星」と
Nettelmannらの「Neptune +」密度プロファイル。 (2013)(黒い一点鎖線の曲線)。

図3.海王星の極半径MoIと
J2。 青い円は良い解決策を示しています。 色はに対応しています
解の間で補間された推定極半径。

図4.極半径と想定されるものとの関係
天王星(ブルーダイヤモンド)と海王星の(均一な)自転周期
(赤い四角)。 破線は最適な曲線を示しています。 The
点線は推定極半径24,973km(天王星)を示しています
と24,341キロ(ネプチューン)。 PVoyに属する自転周期は
黄色の星で強調表示されます。 Helledらの結果。 (2010)
(剛体回転の場合)PHASに基づくものは緑色で表されます
五芒星。
図5.天王星(青色)と海王星(赤色)の推定MoI値。 惑星モデルは、
省略名のx軸(「U」:ウラヌス、「N」:ネプチューン、「cd」:
corr dyn)。 ドットは平均値を示し、標準偏差を示します
ボックスはソリューションの全範囲を示しています。 選択された惑星モデルの場合、黒い水平線はNettelmannのソリューションを表しています。
etal。 (2013)。
4まとめと結論
この作品では、天王星の経験的構造モデルを提示します
密度プロファイルが(up
3)ポリトロープ。これらのモデルを使用して、J6を予測します
とJ8の値と深風の影響を調査し、
推定されたJ6、J8、極半径、MoI、および密度分布の想定回転周期。次に、
J値、惑星の形、および
風の深さ。 J6とJ8を正確に決定することで、風の深さを制限できることを示します。私たち
また、海王星のJ2のより正確な測定値も示しています
J4は、可能なパラメータ空間を大幅に減らすことができます
ソリューションの。天王星の自転周期も示します
とネプチューンは推定値と最も一致しています
極半径。最後に、MoIを正確に測定することで、風の深さをどのように制限できるかを調査します。
天王星と海王星の自転周期。
私たちの主な結果は次のように要約できます。
(i)天王星と海王星のJ6とJ8の予測は、ダイナミクスに強く依存します。正確な測定
J6またはJ8の(数パーセントの相対的な不確実性を伴う)
天王星とネプチューンの風の深さを制限するために必要です。
(ii)天王星の深部内部の密度分布
海王星は自転周期に大きく依存します
ダイナミクスの影響を強く受けます。均一な回転を想定したモデルの場合、風補正を使用することが重要です
重力係数:J
統計2n = Jmeas 2n − Jdyn 2n。
(iii)J2およびJ4のより正確な測定により、さらに
密度分布を制限し、範囲を狭める
天王星のJ6、J8、MoIの予測解のネプチューン。
(iv)天王星と海王星の両方の正確な決定のために
MoIのは、異なるものを区別するために使用できます
自転周期と風の深さを制限します。ために
前者の場合、1%の相対精度が必要ですが、
後者の場合、0.1%の相対精度が必要です。
(v)天王星の一般的に使用される形状と
海王星は、広く使用されている自転周期PVoyとPHASに同意しません。したがって、私たちはその必要性を繰り返します
回転のロバストで独立した測定の
天王星と海王星の時代と形。
将来の作業では、推定された圧力と密度の関係を使用できます
提示された経験的構造モデルを用語で解釈する
構成の。これにより、可能性を探ることができます
天王星と海王星の組成、および識別
組成勾配とそれらの依存性を決定する
想定される自転周期と風の深さ。私たちは
将来の研究でこれに対処します。
最後に、天王星や海王星への専用の宇宙ミッションの必要性を強調します(例:Arridge et al.2014;
マスターズ他2014; Mousis etal。 2018; Hofstadter etal。 2019;
フレッチャー等。 2020)。そのような使命はすべきであると私たちは提案します
惑星の重力場を測定するように設計されている、
J2とJ4の不確実性を減らし、決定する
高階J6とJ8と惑星の形、そして
可能、惑星の自転周期、およびMoI。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます