メトネ (S/2004 S 1)の現在の軌道

土星の小衛星メトネは15:14でミマスと平均運動共鳴の関係にあり軌道要素が長周期で変化している。以下、機械翻訳。
メトネ (S/2004 S 1)の現在の軌道
投稿日:2022年3月22日
探査機カッシーニは土星系で多くの近接小型衛星を発見し、そのうちのいくつかはミマスとの相互作用と惑星の扁平さのためにエキゾチックな軌道状態を示す。この作品は、現在ミマスとの15:14の平均運動共鳴に関与しているメトネに捧げられています。我々は、メトネの現在の軌道を、その軌道上の短期的、共鳴的、長期的重力摂動を分析および同定することによって、深い研究で与える。さらに、土星の非中心場を周回する近接小天体のアンサンブルの運動方程式の完全な数値積分を行います。軌道のスペクトル解析と力学マップにおけるそれらの解釈により、共鳴力学と長期力学の観点からメトネの軌道とダイナミクスを記述することができます。
我々は、メトネの現在の幾何学的軌道が、離心率における強制共鳴成分のためにミマスの軌道と整列しており、膨張した不穏な関数のいくつかの臨界角の同時振動をもたらすことを示す。したがって、共鳴に関連する4つの重要な議論の同時振動を説明する。
ミマス-メトネ共鳴のマッピングは、15:14 Mimas-Methone共鳴のドメインが、～ 0.015より低い離心率に位置し、194,660～194,730 kmの間隔で振動する半長径に位置する共回転共鳴に関連する規則的な運動によって支配されていることを示している。メトネは現在、このサイトの奥深くにあります。
キーワード天体力学・衛星のダイナミクス・土星系


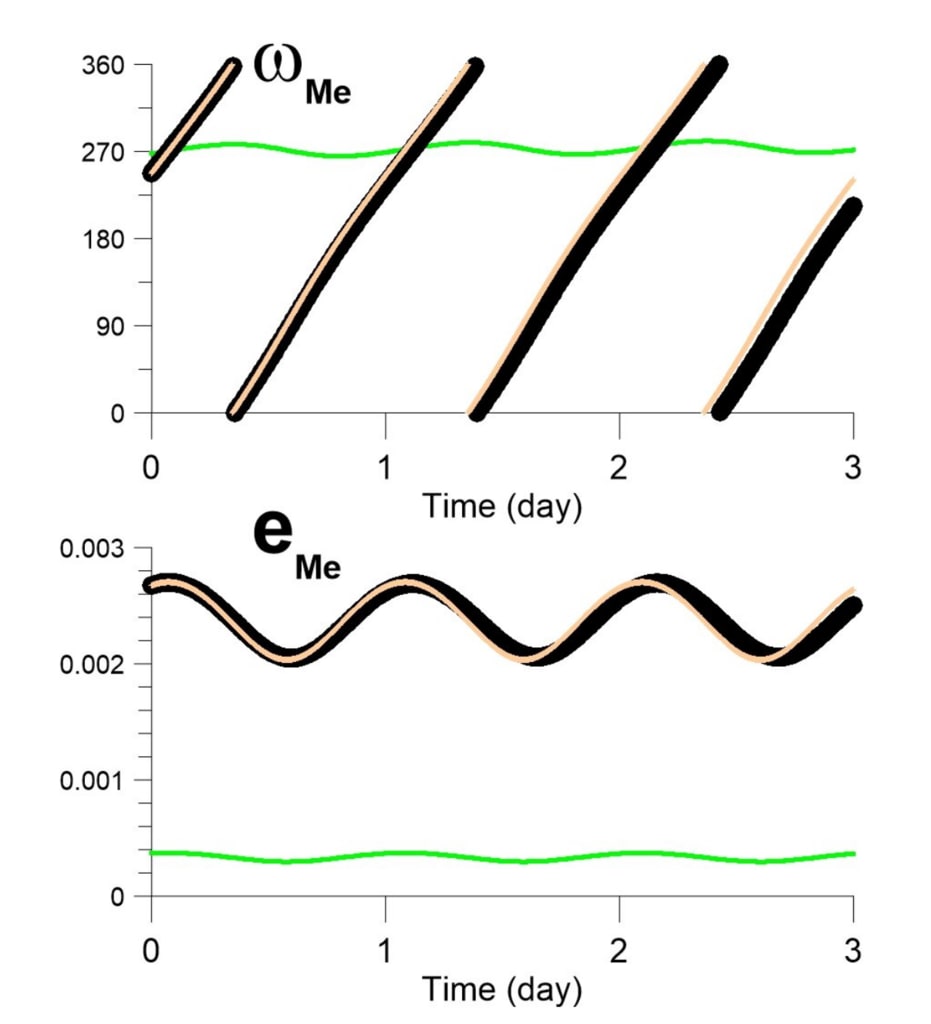
図1近地点引数（上）と軌道離心率（下）
メトネ。 黒の太字の線は、Methoneの接触する中心から取られたものです。
http://ssd.jpl.nasa.gov/horizons.cgi開始時刻は2016年1月1日です。データは
7分のタイムステップで3日間の期間で撮影。 ピンクの曲線は
数値スキームi）から生成され、J2摂動のみが取り入れられています
アカウント。 緑の曲線は、の幾何学的な近心（上）と離心率（下）です。
同じシミュレーションから計算されたMethone。



図2最初の列：Methoneに類似した衛星の振動する半主軸のスペクトル
セクション2）で説明されているMercuryパッケージ（数値スキームii）を使用して計算されます。 初期条件は付録1に示されています。半主軸の振幅はkmで示されています。 合計
統合とサンプリングの時間は、それぞれ1720年と0。06日です。 メインドメイン
論文全体で議論されているスペクトルの内、バルーンで示されています。 主なピーク
表1およびセクション3.1-3.3でも指定され、説明されています。 のさまざまなスケールに注意してください
準主軸のスペクトルのy軸。 2番目の列：振動する離心率のスペクトル（上）と傾斜（下）。



図3左の列と右の列は、それぞれ、数値スキームで計算された、Methoneに類似した衛星の接触および対応する幾何学的要素（表示）を示しています。
i）およびII）、それぞれセクション2で説明されています。 初期条件はから取得されています
2016年1月1日現在のHorizonsシステム。 付録1を参照してください。
接触および幾何学的離心率と準主軸のプロットのy軸。
水平方向の大きな矢印、垂直方向の矢印、および水平方向の小さな矢印については、
それぞれセクション3.1、3.2、3.3.2。



図4図3と同じで、異なる色を使用して4つの臨界角がプロットされています。
ψ1=α− $ M、ψ2= α− $ Me、ψ3=α+ $ Me − 2 $ M、ψ4=α+ $ M − 2 $ Me、ここで
α≡15λMe−14λM。 共振期間と長期期間を強調するために、最初の期間のみ
20,000日が表示されます。



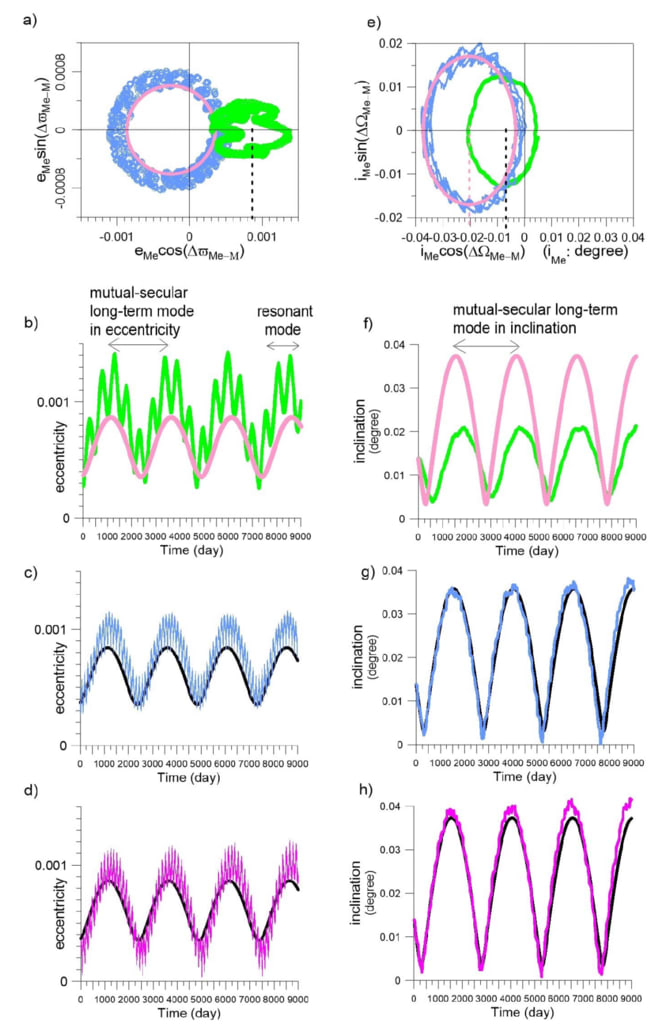
図5緑色の線：図3に示した数値シミュレーションから得られた幾何学的要素。
ピンクと黒の曲線：J2とJ4のオブレート土壷、およびMimasを含む古典的な世俗理論から得られました（セクション4.2を参照）。水色とマゼンタのライン：
最初の振動する準主軸がa0=であることを除いて、緑色の線と同じです。
194,775 km（青）およびa0 = 194,620 km（マゼンタ）。 （a）平面への投影（eMe cos（Δ$ Me-M）、eMe sin（Δ$ Me-M））。垂直の黒い破線は、
幾何学的離心率の強制値。 b）（a）に対応する離心率の時間変化。主な長期モードと共振モードは矢印で示されています。 （c、d）時間
離心率のバリエーション。 （e-h）軌道傾斜角（土星赤道）のプロット。左の列に示されているすべてのケースに対応します。 （e）では、軌道はに投影されます
平面（iMe cos（ΔΩMe-M）、iMe sin（ΔΩMe-M））、および垂直のピンクの破線は
非共振試験衛星の強制傾斜。



図6（a）類似衛星の周縁部の幾何学的経度の時間変化
異なるシミュレーションS1（緑と赤い線）、S2（マゼンタ）、およびS3（黒い点）。 破線と完全な垂直線は、
$iの循環の最初のサイクル。 δは、本文で説明されている約63.5日の差です。 （b）S1から取得した（a）で与えられた同じ変数の対応するフーリエスペクトル。 だけ
〜360.5419日を中心とする主要なピークの周りの短い間隔の詳細（強調表示点線で）表示されています。




図7プロットの上部に示されている個別の変数のスペクトルから構築されたMethoneの1100クローンの個々のパワースペクトル（IPS）。基準振幅は5％、
y軸は対数目盛で示されます。各初期状態の統合時間は
258.376年であり、データは0.09日ごとにサンプリングされています。数値モデル
シミュレーションには、J2、J4、ミマス、エンケラドゥス、テティス、ディオーネ、レアの摂動が含まれます
およびTitan（数値スキームi））、および初期条件はHorizonsから取得されています
2016年1月1日00:00の天体暦のシステム。の現在の構成
プロット内のメトンは、白抜きのひし形で示されています。基本周期の軌跡は垂直方向に分布し、さまざまな記号で識別されます：Pψ1：
15:14ミマス-メトン共回転共鳴。 PΔω、PΔΩ：相互に長期的なミマスメトーン摂動。 P4：2：　4：2ミマス-テティス共鳴の成分（中心
〜33,555.43日=91.87年。 S：短期間の摂動。 VLT：傾斜と離心率の非常に長期的な変動。 H1、H2、H3、H4と高調波の軌跡
異なる基本周波数間。の詳細な説明については、セクション5.1を参照してください。
高調波の正確な組み合わせ、および正確な振幅と周期については表1を参照してください。

6結論
最近発見された土星の小さな軌道の正確な特性
衛星は、惑星科学者の最初からの主要な目標です。
探査機カッシーニによって提供された最初の結果（例：Porco et al。2005、Spitale etal。 2006）。この作品では、私たちはの解釈の改善を提供します
メインを数値的に分析することによるメトネ（S / 2004 S1）その軌道上の重力成分は、主にミマスとの共鳴状態J2土星のフィールド。で与えられたMethoneの現在の軌道の両方を分析しました
HorizonsSystemのようなエフェメリスプラットフォームと数値シミュレーション明確な数値ツールを使用します。
15:14 Mimas-Methoneの平均運動共鳴は、臨界角ψ1≡15λMe−14λM− ωM、これはゼロの周りで解放されます
周期〜521.57日および大振幅〜68度。物理的に、秤動
ψ1の接続詞Mimas-Methoneは、次のような線の周りで発生することを意味します。
常にミマスの中心の方向に振動します。
いわゆる「共回転共振」の典型的な特性。
ψ1の秤動は、私たちが持っている要素のタイプとは無関係に発生します
平均経度から採用された、すなわち、幾何学的または振動的なもの
ミマスとメトネの経度、およびミマスの中心付近の経度、
J2による短期間の変動の影響を受けません。いつ
幾何学的軌道が考慮され、それはの振動時間変動が観察されます
他の3つの幾何学的重要な議論：ψ2=15λMe−14λM− ωMe、ψ3=
15λMe−14λM+ ωMe − 2ωMおよびψ4=15λMe−14λM+ ωM − 2ωMe。
この明らかな相反する共振構成は、角度の組み合わせの表現を次のように再調整することで説明できます。
周辺中心の経度の相対的な変動Δω Me−M = ω Me − ω M：
ψ2=ψ1− ∆ωMe−M、ψ3=ψ1+ ∆ωMe−M、ψ4= ψ1− 2∆ωMe−M。以来
幾何学的な∆ω Me-Mは、周期が約2408.21日で、ゼロ付近で振動します。
結果として生じるψ2、ψ3、およびψ4の時間変化は、2つの周波数、共振周波数と長周期周波数の合成です（明らかに、他のすべてのものを除く）高次および小規模の摂動）。
上記の結論は、共鳴的で世俗的な理論（例：Brouwer and Clemence 1966、Murray and Dermott 1999）これは、近接衛星の特定のケースでは、より一般的です
J2摂動を含むアプローチが必要です。カレガリと横山（2020）小型衛星Antheの軌道の長期変動の解釈に一般化された世俗理論を適用しました。ここでも同じことをします。
∆ωMe-Mの長期振動は、次の場合にのみ保証する必要があります。
Methoneの中心付近の幾何学的経度の長期的な時間変化
Methoneとミマスの場合は似ています。実際、これらの角度のスペクトル分析は、主要なコンポーネントは約360.54日を中心にしています。ミマスの軌道以来
Methoneは数千km離れており、このような対応は主要なコンポーネントは、J2の経年変化だけでは説明できません。
軌道の歳差運動の違いに責任があり、土星からの距離に大きく依存します。経度の循環周期
Methoneのような衛星の中心付近は、J2の摂動のみが原因で、約424.024日となります。この値と現在の値の差
1つは約63.5日であり、15：14によるものであることを数値で示しました。
共回転共振。したがって、共鳴摂動は基本的な役割を果たします　MethoneとMimasの軌道の整列の役割。
15:14Mimas-Methone平均運動のドメインをマッピングしました
位相空間での共鳴。一方向マッピングは、の値を提供します　初期の振動する半主軸の関数としての基本周波数
現在のメトネ軌道のすぐ近くにあります（図7）。最も適切なマッピングは、平面（a0、e0）で定義された動的マップです。
e0は、初期の振動離心率です（図8）。 ψ≡15λs−14λM− ωM、ここで、sはテスト衛星であり、最大間隔でゼロ付近で解放されます。
194,655≤a0≤194,735km　e0 ＜0.015の場合は、共回転ゾーンを区切る15:14Mimas-Methone平均運動共鳴に関連付けられています。
共回転ゾーンの境界は、典型的な非規則的な軌道によって特徴付けられます　共振の分離に関連する運動。この結果は、
以前のものとの良好な一致（例：El Moutamid et al.2014）。 Methoneのorビットは、Corotationの安定した領域の奥深くにあります。
共鳴、それが規則的であることを示しています。