小型カイパーベルト天体の類似物に対する太陽駆動ガス放出による形状進化

遠い天体でも太陽風と太陽光で氷を削ることが出来る？以下、機械翻訳。
小型カイパーベルト天体の類似物に対する太陽駆動ガス放出による形状進化の現象
（2019年12月18日に提出）
木星ファミリー彗星67P /チュリュモフ-ゲラシメンコへのロゼッタのミッションの重要な発見の1つは、大規模な形態における見かけの南北の二分法とともに、その独特な双葉の形状でした。これにより、核の起源、進化、年齢に関する科学的議論が再燃しました。この作業では、全体的な形状変化に対する太陽駆動活動の役割に関する一般的な数値調査を設定しました。私たちの目標は、太陽エネルギーによる質量損失の重要なパラメーターの影響を分離して研究し、できれば最終形状の分類を得ることです。スピン軸および軌道パラメーターのさまざまな初期条件に対して、太陽駆動CO氷昇華を説明する異なる軌道に伝播する5つの一般クラスの3次元（3D）オブジェクトを検討します。2 O ices）も提供されます。この研究で使用される理想化は、特定の特徴または観察の説明に焦点を当てた同様の研究で適用される、活性源の分布、組成、および/または化学的不均一性に関するアドホックな仮定を取り除くことを目的としています。私たちの数値実験は、太陽駆動のガス放出を伴う均一な核は、いかなる条件下でも、凸形状に凹状の形態を生成できることを示しています。一方、既存の凹面は、想定された活動のために平滑化/除去することはほとんどできません。要約すると、太陽の距離、離心率、スピン軸とその向きの間のカップリング、およびシャドウイングと自己発熱への影響が組み合わさって、数値シミュレーションなしでは推定できない形態変化を誘発します。
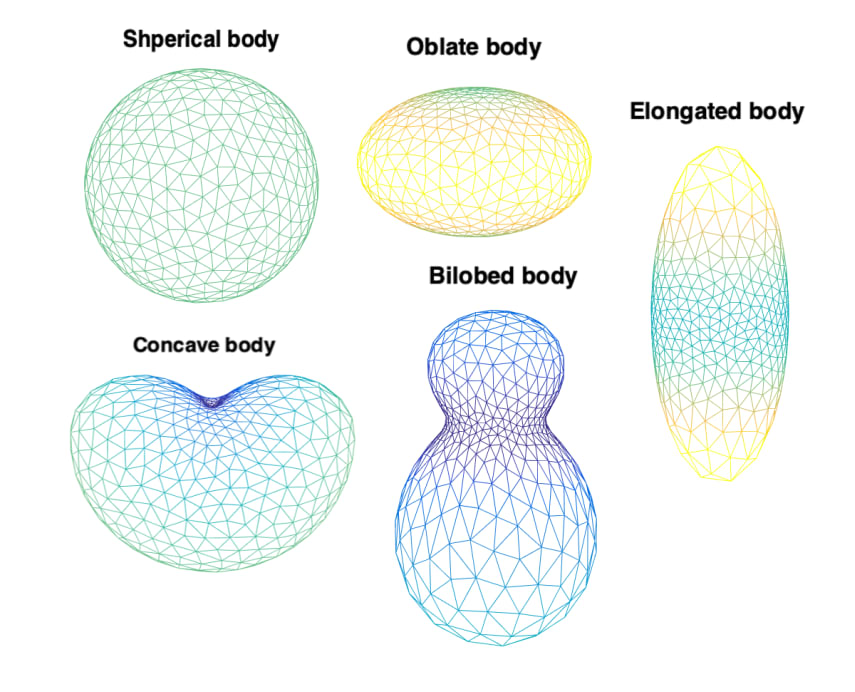
図1.数値シミュレーションで初期ボディとして使用される5つの形状モデル。 エッジの色は表面の高さを示します（身体中心距離、本文の詳細を参照）


図2. CO（黒）およびH2O（青）の質量損失率
太陽フラックスの関数としての昇華。 破線の縦線 ラベルに示されているように、いくつかの太陽中心距離での入射光束値の例として提供されています。 重要な機能
注目すべきは、昇華流束の急激な低下、これらの「膝」曲線。 これらの遷移は非常に異なる値で発生しますが水とCOの流入フラックス（または太陽中心距離）の
これらの曲線と軌道パラメータおよび身体の結合 テキストで説明されているように、方向状態は一般化できます。


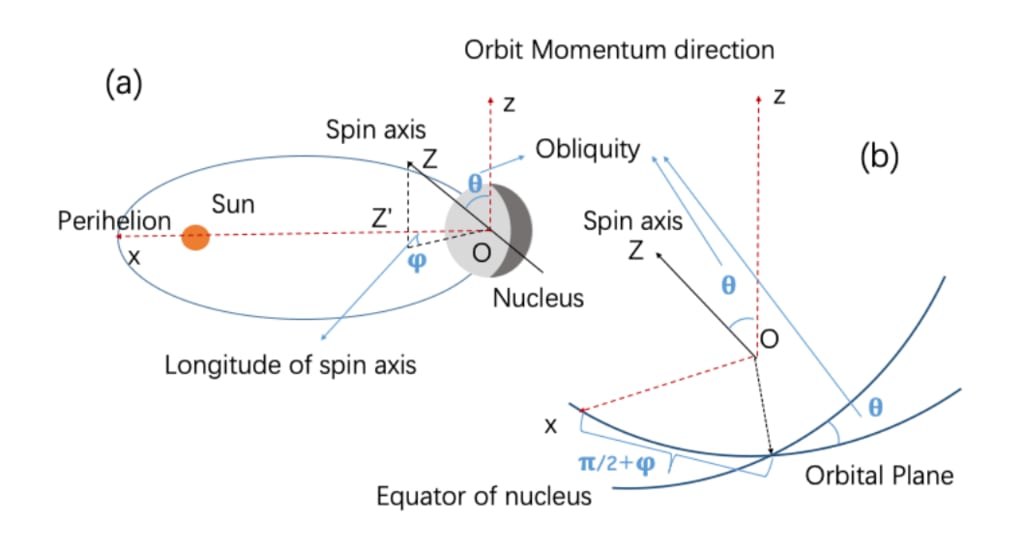
図3.経度ϕおよび核配向の傾斜θ
軌道フレーム。 Oz®とOx®はそれぞれ軌道の運動量方向と近日点を指し、OZ®は回転運動量です。
核の方向、およびスピン軸の方向 主要な回転オブジェクトを考慮します。 OZ®0の投影です
軌道平面上のOZ®、経度theはOZ®0と近日点方向Ox®は右手の法則に従い、斜めθは軌道角運動量と回転の間の角度です
角運動量。 図（a）は、これら2つの角度を示しています。遠日点の核、（b）軌道面と核の赤道、および最初の2つの間の関係を示します
軌道フレームからボディ固定フレームへの転送のオイラー角。


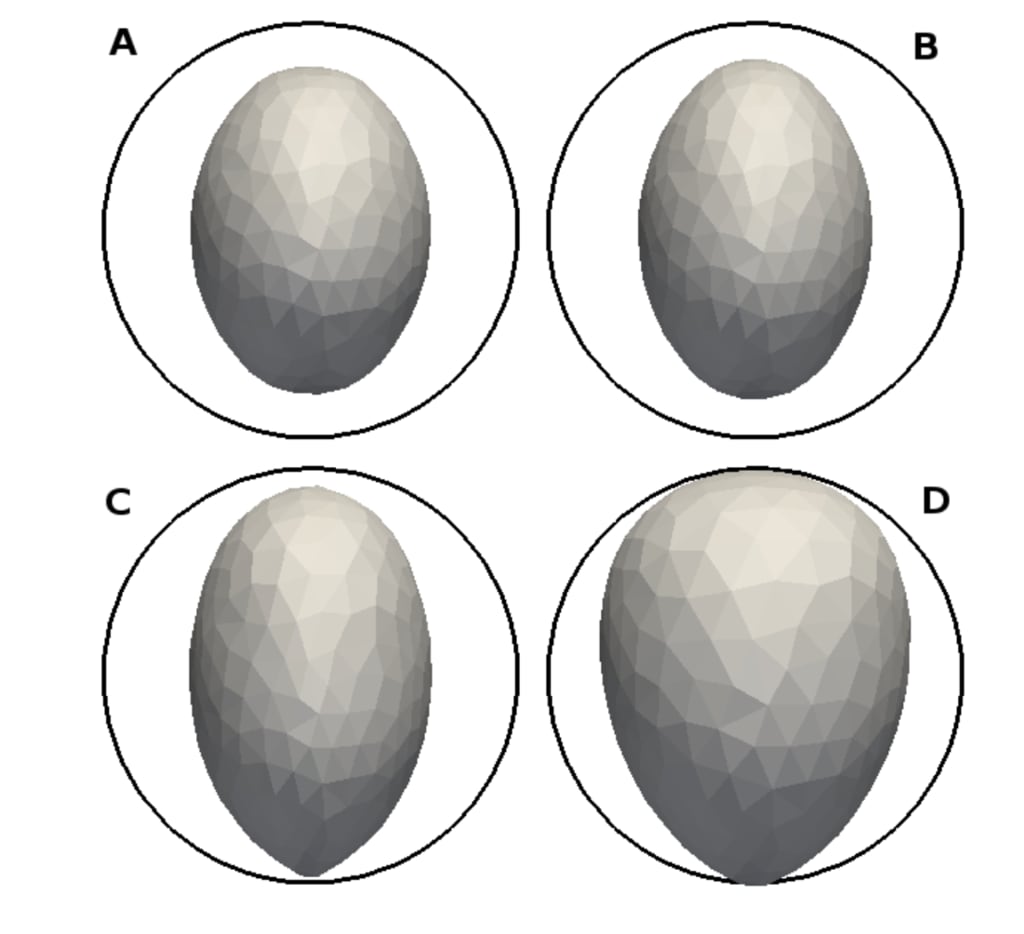
図4.形状変化のさまざまな依存性の例
偏心および半長軸の構成、の場合 細長い本体（長軸に沿った投影図に表示）。
夏の半球（南）は下にあります。 すべての場合 傾斜角、回転軸の経度、離心率は同じであり、
30◦に設定、45◦および0.2。 異なるパネルは異なるだけです。に沿って移動する効果を示す半長軸
図5の一定の偏心。パネルA）a = 25 au、B）a = 75 au、C）a = 175 auおよびD）a = 225 au 黒い円は
視覚的なデモンストレーション用の元のボディ（同じ投影）最終的な形状との違い（説明についてはテキストを参照）。


図7.傾斜（θ）と経度　スピン軸（ϕ）。 円は、元の（球体）ボディのサイズを示します。


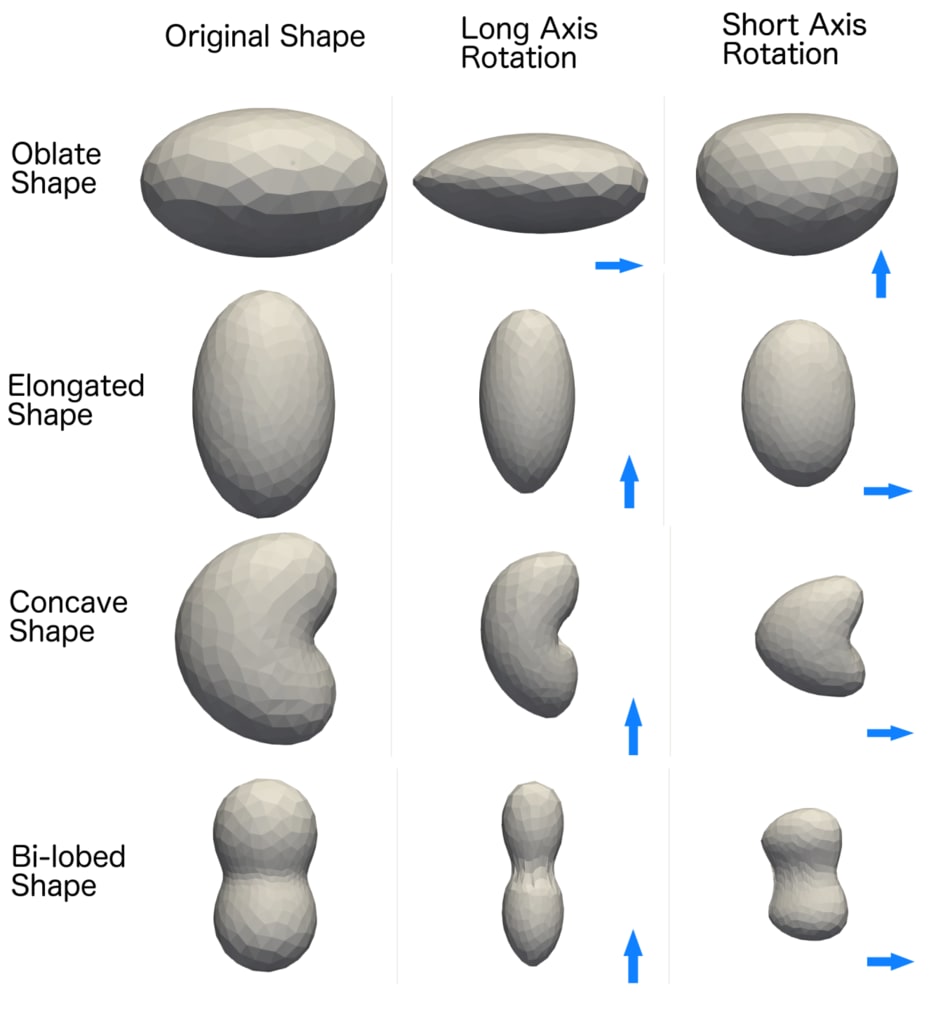
図8.異なるスピン軸構成を持つさまざまな元の形状の核形状の進化。 下部の青い矢印
各パネルの右隅は、南極から北極を指すスピン軸の方向を示しています。 最初の列
は元の形状を示し、2列目は長軸で回転する進化した形状を示し、3列目は形状を示します
短軸回転モードでの進化。 これらのシミュレーションでは、a = 200、e = 0.3、θ=30◦を設定します
、およびϕ = 0◦、したがって、夏半球　これらの体の南です。


図9.シャドウイングと自己発熱を説明する図
さまざまな凹構造の侵食プロセスに効果が働きます。 dとhは、底の寸法と高さです。
凹面、γはそれぞれの傾斜角　底面に関連するエッジ、βは頂点の角度
テキストで詳細に説明した照明コーン。 三　ここにケースが表示されます。グラフィックa）は、エッジが底に対して垂直で、γ= 90◦の穴、グラフィック
b）を記述するために使用できる凹構造を示しています　グラフィックc）はb）の浅いケースですが、クレーターの形状。