
カッシーニによる土星系衛星の観測を下敷きに天王星の衛星に地下海洋が有るか確かめるにはどしたらいいか考察してみたという感じですか。地表の目立つ特徴を目標に平均自転からのズレを検出したり、塩水の海洋が有れば磁気的に検出が可能ということです。以下、機械翻訳。
天王星の最大の衛星の秤動と黄道傾斜角
要約
太陽系で複数の海洋世界が発見され、2023~2032年の惑星科学および宇宙生物学10年計画で天王星が最優先目標に選ばれたことを受けて、天王星の5つの最大の衛星(ミランダ、アリエル、ウンブリエル、チタニア、オベロン)も地下海が存在する可能性があるため、新たな注目を集めています。私たちは、自転測定が天体の内部分化の確認や内部海の存在の検出にどのように役立つかを評価します。天王星の同期衛星の平坦な形状に対する時間的に変化する重力トルクにより、衛星は平均自転に対して秤動し、黄道傾斜角がゼロではない状態で歳差運動します。岩石の核を水圏で囲んだ固体または外側の氷の殻に分かれ、その下に液体の海があるさまざまな内部モデルについて、日周の秤動振幅と傾斜角を計算します。天王星の衛星が 2 層の固体であれば、オベロンの約 0.25 m からミランダの約 6 m までの秤動測定精度から、均質な内部空間が存在する可能性は排除されます。平均慣性モーメント (MOI) の独立した推定値と組み合わせることで、秤動測定を使用して海の存在を検出することもできますが、これに必要な測定精度は、秤動振幅の実際の値によって異なります。傾斜角を計算するには、まず永年摂動モデルを使用して、5 つの衛星すべての軌道歳差運動の系列を作成します。ミランダを除いて、衛星間の重力相互作用により、天王星の大型衛星の傾斜角は平均値の周りで比較的大きな周期的変動を示すことが示されています。アリエルの約 1 メートルからオベロンの約 400 メートルまでの傾斜角測定精度により、均質なケースを除外できることがわかっています。地球内部の海洋の存在により、傾斜角の共鳴増幅が可能になり、検出が容易になります。このような共鳴が発生しない場合、傾斜角は固体の場合とほとんど区別がつかなくなります。潮汐変形が小型から中型の天王星の衛星の自転に与える影響は限られていることが示されています。ティタニアとオベロンでは、秤動が最大 10% 減少し、傾斜角が最大 15% 増加しますが、ミランダではその影響は無視できます。
1. はじめに
ミランダ、アリエル、ウンブリエル、ティタニア、オベロンは、英語文学の登場人物にちなんで名付けられた天王星の 5 つの最大の衛星です。これらは小型または中型の氷衛星で、まだほとんど何もわかっていません。ウィリアム ハーシェル (ティタニアとオベロン、1787 年)、ウィリアム ラッセル (アリエルとウンブリエル、1851 年)、ジェラルド カイパー (ミランダ、1948 年) によって発見されましたが、1986 年にボイジャー 2 号が天王星をフライバイした際に、宇宙探査ミッションによって一度だけ訪問されました。
過去数十年間で、太陽系の外縁部、木星と土星の氷衛星の表面下で水が液体の状態で存在できることがわかっています (Nimmo と Pappalardo、2016 年)。ガリレオ計画は木星の衛星システムを広範囲に調査し、エウロパ、ガニメデ、カリスト付近で誘導磁場を発見し、地下海の存在を示唆しました (Khurana 他、1998 年、Kivelson 他、2002 年)。磁気誘導は、これらの海を検出するための複数の手法の 1 つにすぎません。エウロパとその「氷山」の場合のように、表面を観察すると刺激的なことがあります (Carr 他、1998 年)。最近のハッブル宇宙望遠鏡 (HST) によるガニメデのオーロラオーバルの低振幅振動の観測は、厚い氷の層の下に地下海が存在することを示しています (Saur 他、2015 年)。カッシーニ計画は、氷の衛星の地下海を検出するために使用される手法の範囲を拡大しました。小型のエンケラドゥスは異常に暖かい南極で異常な活動を示し、水蒸気と氷粒子の噴出は、地表の下に液体の水があり、その下にある岩石の核と接触している証拠であると解釈されています (Porco et al., 2006; Spencer et al., 2006, 2009; Postberg et al., 2011)。エンケラドゥスの形状、重力場、日周振動は、厚さ約 20 ~ 30 km の氷殻の下に地球規模の水の貯留層があることと一致しています (Park et al. (2024) およびそこに記載されている参考文献)。ディオネの重力と形状は、地球規模の水の海を覆う氷殻の観点からも説明できます (Beuthe et al., 2016; Zannoni et al., 2020)。観測されたタイタンの傾斜角は、完全に固体で硬いタイタンに予想される傾斜角の約 3 倍です (Baland 他 (2019) およびその中の参考文献)。衛星が経験した大きな日周潮汐変形も、タイタン内部に地球規模の海が存在することを証明しています (Iess 他、2012 年、Durante 他、2019 年、Goossens 他、2024 年)。一方、地球規模の海を覆う厚い氷の殻は、ホイヘンス探査機による電場測定を説明しています (B´eghin 他、2012 年)。海を持つ氷衛星のクラブに最近加わったのは、多数のクレーターがあるミマスかもしれません。その秤動は深部に液体層が存在することと一致する可能性があり(Tajeddine et al., 2014)、軌道の進化は地表から20〜30 kmの深さに非常に若い海が存在することを示唆している(Lainey)。ボイジャー、ガリレオ、カッシーニ・ホイヘンスはフラッグシップクラスのミッションでした。海王星、天王星、およびそれらの衛星は、野心的な探査ミッションをまだ待っています。天王星探査機(UOP)は、2023〜2033年の惑星科学および宇宙生物学10年調査(米国科学、工学、医学アカデミー、2023年)によって、次のフラッグシップクラスのミッションとして優先されています。とりわけ、このミッションは、4年間のツアー中に、5つの最大の衛星に関する重要な質問に取り組むことを目指します。それらの岩石と氷の質量比と内部構造は?どの衛星に内部海があるか?これらの質問への答えは、それらの形成と進化を制限するのにも役立ちます。
この論文では、将来のUOP宇宙船のペイロードの一部となる狭角カメラと広角カメラ(NACとWAC)で取得した画像からランドマーク追跡などの手法で推定できる、天王星最大の衛星の回転観測可能範囲(秤動と黄道傾斜)を定義することを目的としています。光学データは、宇宙船に搭載された無線科学実験の放射測定データと併用して、衛星の内部を推測することができます(Filice et al.、2024)。この研究では考慮されていませんが、磁気誘導も、天王星の最大の衛星内の地下海を調査するために提案されています(例:Cochrane et al.(2021)。
この論文は次のように構成されています。セクション 2 では、既存の文献に基づいて、各衛星の 3 層内部 (シェル、海洋、コア) の範囲を定義し、静水圧平衡にあると想定します。内部は質量と半径によって制約され、総平均慣性モーメント (MOI) と次数 2 の重力係数、および各層の密度、寸法、平坦度によって特徴付けられます。以前の研究では、海洋と氷殻の密度の違いの影響は調査されていませんでした。これが、水圏の厚さやグローバルな差異の観点から推定された MOI と重力係数の解釈にどのように影響するかについて簡単に説明します。セクション 3 では、衛星がカッシーニ状態に固定されていると想定して、セクション 2 で定義した 3 層内部の固体層 (シェルとコア) の日周振動の振幅と傾斜角を計算します。回転測定に必要な精度について議論し、これらの測定を内部特性や全体的差異の観点から解釈できるようにします。結論はセクション 4 で示し、私たちの秤動測定結果と Hemingway と Nimmo (2024) による最近の研究との類似点と相違点について議論します。
2. 衛星の内部と重力場
2.1. 質量、半径、平均密度
天王星の 5 つの最大の衛星の内部に関する主な観測上の制約は、質量と半径です (表 1 を参照)。地球ベースの天体測定、ボイジャー 2 号の観測、および Jacobson (2014) によるリング掩蔽から、それらの軌道と質量を決定しました。リム座標から 5 つの衛星の形状と半径の推定は、ボイジャー 2 号の時代にまで遡ります (Thomas、1988)。恒星掩蔽解析に基づくウンブリエルの平均半径の最新値は、Assafin et al. (2023) で報告されていますが、統計的には以前の推定値と変わりません。質量と半径から得られた密度と表面の観測結果を組み合わせると、衛星の構成と内部構造に関する最初の兆候が得られます。アリエル、ウンブリエル、チタニア、オベロンは中型の衛星で、密度が低いことから内部は主に水氷でできていることがわかります。一方、ミランダはエンケラドゥスやミマスのような小型衛星ですが、密度が低く、したがって岩石と氷の比率も低くなっています (Hussmann et al., 2006)。

表 1: 天王星の 5 つの大きな衛星の赤道半径と極半径 (a > b > c)、平均半径 R、重力パラメータ GM、平均密度 ¯ρ。Thomas (1988) および Jacobson (2014) による。
2.2. 慣性モーメントと重力場
正規化された平均慣性モーメント MOI = I/MR^2
は内部分化の指標であり、天王星の衛星についてはまだ決定されていません。約 0.3 から 0.4 の間で変化すると考えられます (たとえば、分化の観点から 2 つの端の要素であるガニメデとカリストではそれぞれ 0.31 と 0.36、(Schubert ら、2004))。

図 1: 天王星の衛星の非正規化重力係数 J2 と C22 を、静水圧平衡を仮定して式 (1) から計算した、正規化平均慣性モーメント I/MR^2 の関数として表したもの。点は、Chen ら (2014) の C/MR^2 (ここでは I/MR^2 の代理として採用) = 0.33 の値を示しています。灰色の破線は、ディオネの推定値 (Zannoni ら、2020) を示しています。静水圧平衡を仮定すると、重力場の係数 J2 と C22 の値は、I/MR^2 の任意の値に対して、ラダウの方程式と J2 と C22 の静水圧関係 (例: Van Hoolst ら (2008)) から取得できます。

ここで、qr = n^2R^3/GM は遠心加速度と重力加速度の比で、n は平均運動、R は平均半径、GM は重力パラメータです。注意:
Radau の式は、次数 2 の重力係数を、文献でよく見られる極慣性モーメント (C/MR^2 = I/MR^2 + 2J2/3) ではなく、正規化された平均慣性モーメント (I/MR^2) に関連付けます (例: Castillo-Rogez ら (2023) の式 7)。Van Hoolst ら (2008) の式 (47) の後の議論を参照してください)。図 1 は、5 つの衛星の J2 および C22 範囲を I/MR^2 の関数として示しています。ここでは、同じ仮説に基づく以前の推定値 (Chen et al., 2014; Castillo-Rogez et al.,2023) と一致する値を得ています。これらの計算は、主に桁数を特定することを目的としています。衛星の内部構造や、衛星が何層に分割されているかについての仮定は必要ありません。このようにして得られた桁数は、土星の衛星でアリエルやウンブリエルとほぼ同じ大きさのディオネの重力係数と一致しますが、ディオネは静水圧平衡を満たさないことが知られています (Zannoni et al., 2020)。ミランダとアリエルの楕円形 (a > b > c) は、Thomas (1988) によって推定されました。ボイジャー2号が衛星を部分的にカバーしたことを考えると、これらの形状が静水圧平衡仮説と一致するかどうかを確実に結論付けることは困難であり、おそらくa、b、cに関する形式的な不確実性が小さいことはいくぶん楽観的である。Castillo-Rogez et al. (2023)と同様に、a、b、cの個々の値は静水圧平衡に期待される値と一致することがわかった(図2を参照)。Castillo-Rogez et al. (2023)とは異なり、(b − c)/(a − c)の組み合わせ(ミランダとアリエルの場合はそれぞれ0.17 ± 0.17と0.06 ± 0.33)も、期待される静水圧値0.25と一致することがわかった。明確な反証が得られるまでは、以下に示すように、天王星の大型衛星の回転をモデル化する際に、これらの衛星が静水圧平衡にあると仮定するのが妥当である。

図 2: ミランダとアリエルの赤道半径と極半径 (a > b > c) を MOI (I/MR2) の関数として表したもの。Van Hoolst ら (2008) の式 (35) で定義され、式 (3) と平均半径 R = (a+b+c)/3 から計算され、静水圧平衡 (実線) を仮定しています。網掛け部分は Thomas (1988) による 1σ の推定値に対応しています。
2.3. 3 層内部
Hussmann ら (2006)、Bierson と Nimmo (2022)、Castillo-Rogez ら (2023) に従い、ここでは衛星がすべて岩石コアと外部水圏に分化していると仮定します。
水圏は、完全に氷 I マントルであるか、氷 I 殻と岩石核に接する液体の水の海に分かれています。 Hussmann ら (2006)、Bierson と Nimmo (2022)、Castillo-Rogez ら (2023) は、液体の海の可能性について異なる結論に達しています。 Hussmann ら (2006) と Bierson と Nimmo (2022) によると、水の海は少なくとも 100 km の厚さの氷殻の下にある Titania と Oberon でのみ可能です。 Castillo-Rogez ら (2023) は、厚い (> 200 km) 氷殻の下にある、Ariel と Umbriel では 30 km 未満の厚さの深海、Titania と Oberon では 50 km 未満の深海が残ると予測しています。ビアソンとニモ(2022)は、カスティーヨ・ロジェスら(2023)とは対照的に、他の衛星の海洋を維持するのに役立つ可能性のある潮汐加熱を無視するという保守的なアプローチを採用していることに留意すべきである。ミランダの衛星は非常に小さく、潮汐共鳴の外では、わずか数十億年で海洋が凍結するため、ミランダの地下海洋の可能性はすべて排除されている。この探索的研究では、2層または3層の密度と寸法について比較的保守的な範囲を検討し、これらのパラメータが自転に与える影響を説明することを目指している。その精神で、ミランダには液体の海洋が存在する可能性もあると考えている。氷と水の密度範囲は広く(700~1050 kg m−3、最も低い密度は多孔性が高いことを意味し、最も高い密度はアンモニアや塩などの不純物が存在することを意味する)、Castillo-Rogez ら(2023)がセクション 6.1 で水圏に使用した範囲に従います。これらの著者とは異なり、ここでは水と氷の間の可変密度コントラスト(ρo ≥ ρs)の影響を検討します。岩石の密度範囲は、Hussmann ら(2006)や Bierson と Nimmo(2022)と同様に、2400 kg m^−3(Castillo-Rogez ら(2023)の最小値)から 3500 kg m−3 までです。Castillo-Rogez らに従い、海の厚さは最大 50 km と見なします。 (2023)。
3層内部のセットを構築するには、まず海洋の厚さhoを2.5~50 kmに設定し、次に氷、水、岩石の密度と総半径および質量の制約から氷殻の厚さhsと岩石コアの半径Rc = R − hs − hoを導き出します。海洋の厚さは制限されている(ho ≤ 50 km)ように選択されているため、氷殻は5つの衛星すべてで比較的厚くなります(ミランダの場合はhs ≳ 30 km、その他の衛星の場合はhs ≳ 70 km、表2を参照)。3層内部のMOIは(例:Van Hoolst et al. 2008)で与えられ、

Ro = R − hs、平均海洋半径です。差別化された内部のセットのMOIと重力係数の範囲は、均質な物体の値よりも小さくなります。この研究では、圧力が物質の密度に与える影響を無視しているため、組成に関して完全に均質な物体は密度が均一で、MOI は 0.4 になります。

表 2: 本研究で回転観測量の計算に考慮した天王星衛星内部の 3 層の密度と寸法の範囲。総 MOI の範囲と次数 2 の重力係数 J2 と C22 も示し、同じ質量と半径の均質衛星の値と比較します。
私たちの 3 層内部範囲は基本的に Castillo-Rogez ら (2023) の 2 層内部範囲の保守的な拡張であるため、ここでは将来のミッションの観測量としての MOI と C22 に関するセクション 6.1 で開始された議論を続けます。C22 は宇宙ミッションで実施された電波科学実験の古典的な結果ですが、MOI は静水力学的仮定が適用される場合、ラダウ方程式を使用して C22 から導き出すことができます (セクション 2.2 を参照)。
Castillo-Rogez らの図 11 に示されている MOI と岩石コア密度および水圏の厚さの関係は、Castillo-Rogez らの図 12 で示されています。 (2023) は、岩石コアと水圏を持つ 2 層モデルに関するものです。これらの 2 層モデルは、質量分布の点で、殻と海洋の密度が等しい 3 層モデルと同一です。図 3 では、殻と海洋の密度差も含む 3 層内部の MOI と ρc および hs + ho の関係を示しています。氷と水の密度に対する制約が限られているため、MOI から内部を制約できる可能性は疑問です。Castillo-Rogez ら (2023) と同様に、ここでは将来の MOI 決定の精度を ±0.005 と見なしています。これは約 1.5% の誤差に相当し、エンケラドゥスやディオネなどの小さな氷衛星の重力場決定の実際の精度を考えると妥当と思われます (Iess ら、2012 年、Zannini ら、2020 年)。ここで、岩石密度と殻と海洋の密度の対比について考慮した保守的な範囲では、MOI の精度 ±0.005 は、ミランダの水圏の厚さの不確実性約 30 km に相当します (Castillo-Rogez ら (2023) で報告された 15 km に対して)。また、殻の密度が 50 kg/m3 よりも高い精度で決定されたとしても、海洋の密度は小さい ρs に対して本質的に制約を受けません。中型衛星の Ariel、Umbriel、Titania、Oberon の場合、MOI の精度 ±0.005 は、Castillo-Rogez ら (2023) ですでに示されているように、水圏の厚さの不確実性 50 km に相当します。ミランダの場合と同様に、ここで行っているように、より高い最大コア密度を考慮すると、特定の MOI に対して許容される水圏の厚さの範囲が広がる傾向があることに注意してください。内部パラメータ、つまり氷水/岩石比を決定できない場合、物体が均質であるか分化しているかを少なくとも決定することはできるでしょうか。これは、Castillo-Rogez ら (2023) が MOI の関数として C22 の図 12 で取り上げている問題です。まず、静水圧平衡を仮定すると、MOI 情報は C22 情報と完全に同等であることを指摘したいと思います。Castillo-Rogez ら (2023) の図 12 は、図 1 に示すように詳細な内部構造に依存しない Radau の関係を示しています。したがって、ここでは MOI に焦点を当てて議論します。MOI に必要な精度は、均質な対応値 0.40 に対するパラメータの実際の値に依存します。Miranda を除いて、すべての MOI 値は、岩石密度が低い場合でも 0.34 未満です。 MOI 値が低いほど、均質な物体と分化した物体を区別しやすくなります。値が 0.4 に近いほど、測定の精度が高くなるためです。たとえば、Oberon の MOI が 0.34 の場合、分化した内部と均質な内部を区別するには、0.06 以下の精度が必要です。Miranda の MOI が 0.29 の場合、0.11 未満の精度で十分です。C22 では、それぞれ 0.8 × 10−5 と 170 × 10−5 の精度になります。
2.4. 平坦化
静水圧平衡にある 3 層の同期衛星の回転をモデル化するには、その層の慣性モーメントを計算する必要があります。これは、表面の極 (α) および赤道 (β) の平坦化と、殻と海洋、海洋とコアの楕円体界面の平坦化に依存します。この論文の残りの部分では、下付き文字 s、o、c は、それぞれ表面、海洋半径、コア半径の平坦化を表します。同期衛星は、回転と静潮の両方によって平坦化されます。表面の極 (αs) および赤道 (βs) の平坦化は、次のように定義されます (Van Hoolst et al.、2008)
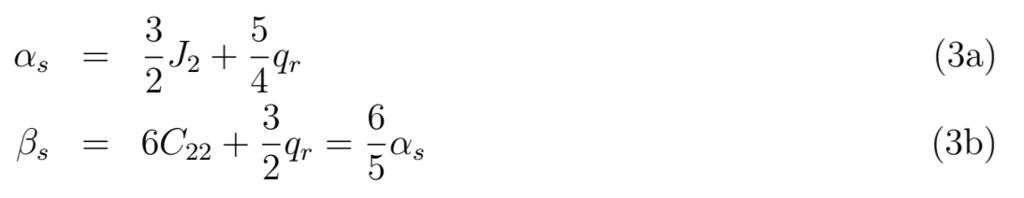
したがって、重力係数を通じて MOI と一義的に関連しています。極および/または赤道幾何学的平坦化を J2 および C22 重力係数よりも正確に測定できれば、ラダウ方程式を使用して MOI を導くために使用できます。海洋半径 Ro (αo、βo) およびコア半径 Rc (αc、βc) での平坦化は、クレローの微分方程式を積分することによって得られます。関係 β = 6α/5 は、どの深さでも有効です (詳細は Van Hoolst ら (2008) を参照)。
図 4 の右パネルは、ミランダの場合の極平坦化と深さの関係を示しています。端メンバー 3 層内部の密度プロファイルは左パネルに示されています。
中心から表面に向かって α が増加することがわかります。αs は MOI の減少とともに減少し、したがってシェル密度 ρs の減少とともに減少する傾向があります。シェルと海洋の密度のコントラストもシェルの平坦化に影響する可能性があります (特に MOI が大きい場合) が、考慮される最小および最大 MOI によって許容される範囲内に常に留まります。

図 3: 表 2 で定義される、3 層のミランダ、アリエル (ウンブリエルの代理)、チタニア (オベロンの代理) の岩石コア密度 ρc (左パネル) と水圏の厚さ hs + ho (右パネル) の関数としての MOI。この図は、Castillo-Rogez ら (2023) の図 11 に基づいています。線は、下から上に向かって、50 kg/m3 刻みで ρs = 700 kg/m^3 から 1050 kg/m^3 に対応しています (実線と破線の場合はそれぞれ ρo = ρs と ρo = 1050 kg/m3)。破線は、固定された海洋の厚さ ho = 50 km にも対応しており、密度のコントラストが MOI に及ぼす最大の影響を示しています。
2.5。潮汐ラブ数 k2
天王星の重力場は衛星の周期的な変形の原因であり、その結果、衛星の重力ポテンシャルの周期的な変動が潮汐ラブ数 k2 に比例します。k2 値が小さいということは、変形がほとんどないかなり硬い物体であることを示します。同期衛星の回転は潮汐変形に依存します。周期的な変形の膨らみがさまざまな層で発生する結合に影響を与えるためです。周期的な潮汐変形が大型衛星の回転に与える影響は非常に重要になる場合がありますが (秤動については Van Hoolst 他 (2013) を参照)、エンケラドゥスのような小型衛星では影響は小さくなります (Van Hoolst 他、2016 年、Baland 他、

図 4: ミランダの密度 (左) と極の平坦化 (右) を半径の関数として、最小 (青の実線: ρs = ρo = 700 kg/m^3、ρc = 3500 kg/m^3、ho = 50 km) および最大 (オレンジの実線:ρs = ρo = 1050 kg/m^3、ρc = 2400 kg/m^3、ho = 2.5 km) の MOI を持つ内部で示しています。破線の青とオレンジの線は、同様の内部に対応していますが、それぞれ ρo = 1050 kg/m^3 と ρs = 700 kg/m^3です。
2016)。したがって、ミランダでも小さく、中型の天王星の衛星ではやや大きくなると予想されます。弾性効果は第 3 章で秤動に及ぼす影響を定量化します。
2 層体について Hussmann ら (2006) が報告した値を含む k2 の範囲と、3 層モデルで得た結果を検討し、海洋の有無にかかわらず、潮汐変形が回転に及ぼす影響の可能性について議論します。粘性の影響については、天王星の衛星のラブ数の詳細な計算が目的ではないため、ここでは取り上げません。
剛性 µ の均質体の場合、潮汐ラブ数は次のように表すことができます。Melchior(1973)

天王星の衛星の値は、表 3 の 2 番目の列に示されており、µ = 4×10^9 Pa (純粋な氷を最もよく表す値) です。これは Chen ら (2014) の値と一致しています。2 層の固体の場合、k2 のコア半径 (または同等の氷マントルの厚さ) への依存性は絶対値では小さいです。したがって、Hussmann ら (2006) によって提供され、表 3 の 3 番目の列に報告されている固有の値のみを考慮します。液体の海を持つ 3 層の物体の場合、標準的なプロパゲーター マトリックス手法 (例: Sabadini ら (2016)) を使用します。Hussmann ら (2006) に従い、シェルとコアの剛性としてそれぞれ µs = 3.3×10^9 Pa、µc = 50×10^9 Pa を使用します。 ρs = ρo の場合、Beuthe (2015) の均質地殻モデル (付録 A を参照) は、標準モデルと比較して約 1% の精度です。均質地殻モデルはコアの半径と密度に明示的に依存しないため、これらのパラメータに関連して大きく変化しない標準モデルで得られた結果に光を当てます。一般モデルで得られた範囲は、表 3 の列 4 に示されています。3 層の k2 は、以前のモデルに全球の地下海洋が含まれているため、2 層の k2 の 2 ~ 20 倍大きくなりますが、均質ケースの値は 3 層ケースの最低値に似ています。 3層の場合、図5に示すように、シェルの厚さhsが減少するにつれてk2が増加します。
k2は、ミランダでは約0.004、アリエルとウンブリエルでは0.035、チタニアとオベロンでは0.07まで大きくなります。最低値(ミランダでは約0.0008、アリエルとウンブリエルでは0.008、オベロンでは0.016)は、後者の場合、剛性を考慮した結果として、k2 は均質の場合に近くなります。k2 は、氷の剛性と氷および海洋の密度に依存しますが、その程度は均質の場合より低くなります。剛性が減少すると、k2 は増加します (ここでは示されていません)。シェルと海洋の密度が高いほど、潮汐ラブ数が大きくなることが予想されますが、密度の高いシェルと海洋は質量制約を満たすためにシェルが厚くなることを意味し、これにより、内部モデル セットでの k2 の増加が緩和されることに留意する必要があります。

表 3: 各衛星のラブ数 k2。固体均質ケース (2 番目の列)、固体 2 層ケース (3 番目の列 - Hussmann ら (2006) の値)、および液体の海がある 3 層ケース (最後の列)。

図 5: 表 2 で定義される 3 層内部の氷殻厚さ hs の関数としてのラブ数 k2。
色付きの実線は、ρo = ρs の場合に対応します (値はカラー コードで示されます)。色付きの破線は、同じ殻密度と ρo = 1050 kg/m^3 の場合に対応します。黒の実線と破線は、表 3 で報告されている 2 層および均質固体の場合に対応します。
3. 自転
天王星の赤道は、その軌道面に対してほぼ直角です。天王星の 5 つの大きな衛星の軌道は、天王星の赤道とほぼ同一平面にあり、離心率は比較的小さいです。傾斜は 0.30 度未満です (傾斜が 4.4 ◦ のミランダを除く)。ボイジャー 2 号が撮影した画像により、これらの衛星は月と同様に同期回転しており、その回転軸は天王星の自転軸とほぼ平行であるという理論上の予想が確認されました (Smith ら、1986 年)。また、これらの衛星は、低傾斜カッシーニ状態に閉じ込められている可能性も高いとされています (Gomes と Correia (2024 年) を参照)。次のサブセクションでは、これらの衛星の強制日周振動と自転歳差運動について調べます。この研究には、ガリレオ衛星、タイタン、エンケラドゥスなどに適用された、以前に公開された回転モデルを使用します。
3.1. 軌道モデル
回転モデルの入力として、URA111 エフェメリス (Jacobson、2014 年) から得られた軌道パラメータを使用します。衛星の軌道を記述するために必要な詳細レベルは、モデル化の目的によって異なります。秤動に関しては、ケプラー軌道上の衛星の回転の変動に対応する日周成分のみをモデル化します。軌道摂動により、他の周期の秤動も存在します。日周秤動は周期が短いため、宇宙ミッション データ内の他の変動とは異なる信号として識別できます (例: Thomas 他 (2016))。また、衛星の内部構造に最も依存するのは回転変動です (長周期の秤動は、内部モードとの共鳴が存在しない限り、内部構造にほとんど依存しません)。日周秤動をモデル化するには、Jacobson (2014) の表 2 に示され、ここで表 4 に再現されている平均軌道離心率 e と平均運動 n のみが関連します。

表 4: 平均軌道離心率 e、平均運動 n、公転周期 (Jacobson、2014)。
スピン歳差運動と傾斜角に関しては、衛星の軌道の説明にはより注意が必要です。衛星の傾斜角とスピン歳差運動は、傾斜角と軌道歳差運動によって決まります。Jacobson (2014) の表 2 にある、時間に依存しない傾斜角と歳差運動率を持つ平均軌道要素は、この文脈では適切な表現ではありません。軌道歳差運動は必ずしも均一ではなく、傾斜角は軌道周期よりもはるかに長い期間にわたって変化します。その結果、傾斜角も長期間にわたって変化します。将来の宇宙船の観測から傾斜角を予測するには、これらの変化をモデル化する必要があります。訪問宇宙船から得られる傾斜角の瞬間値 (または比較的短い期間の平均) に関する情報のみに注意してください (例: Stiles ら (2008))。スピン歳差運動と傾斜角をモデル化するために、永年摂動モデルで構築された軌道歳差運動の系列を使用することにしました。付録
付録 A を参照してください。
3.2. 日周秤動
同期衛星が偏心軌道に沿って公転すると、その長軸が惑星の中心を正確に指していないため、惑星は時間とともに変化する重力トルクを衛星に及ぼし、日周の縦方向秤動を引き起こします (例: Comstock and Bills (2003))。内部海洋またはその他のグローバル流体層が存在する場合、外部重力トルクに対する応答は、衛星の異なる層間の結合によって変化します。日周秤動の振幅は、天体とその層の周期的な変形によっても影響を受けます。
3.2.1. 固体の場合
完全に固体で剛性のある同期衛星の強制日周振動の振幅は、次のように表されます (例: Van Hoolst 他 (2008))
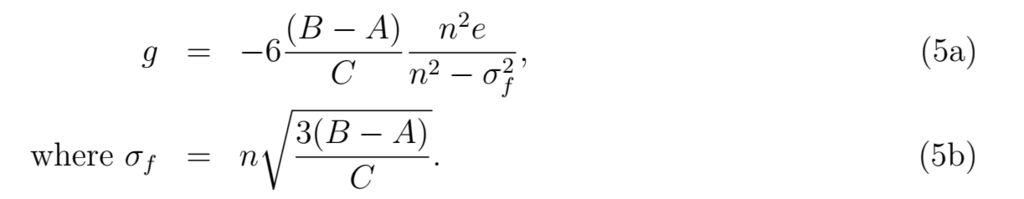
振幅 g は、軌道離心率 e と衛星の赤道慣性モーメントの差 (A < B) に比例し、極慣性モーメント C に反比例します。 (B − A) と e は、親惑星によって及ぼされる重力トルクの強さを表し、C は、加えられたトルクに対する衛星の抵抗を表します。 σf は、自由振動の固有周波数です。固体で剛性のある衛星の振動振幅は、内部構造を特徴付けるさまざまな層の密度とサイズに直接依存せず、主慣性モーメントのみに依存します。したがって、静水圧平衡を仮定すると、ラダウの方程式から、特定の衛星の秤動振幅は MOI のみに依存することがわかります。密度プロファイルが異なるが同じ MOI を持つ 2 つの内部は、同じ秤動振幅を持ちます。天王星の衛星が剛体で均質な物体である場合、その秤動振幅は、表面でオベロンの約 1 m からミランダの 62 m の範囲になります (表 5 を参照)。固体の秤動振幅は、自由周期が強制周期の約 4 (ミランダ) から 45 (オベロン) 倍長く、g ≃ −6e(B − A)/C であるため、共鳴効果がほとんどまたはまったくありません。一般的な規則として、同期衛星が惑星に近いほど、自転速度が速くなり、差 (B − A)/MR2 が大きくなり、秤動振幅が大きくなります。特に大きな離心率を持つ衛星は、この規則に反する可能性があります (たとえば、ウンブリエルの離心率はアリエルのほぼ 4 倍であるため、その秤動振幅も大きくなります)。2 層に分化した天体の場合、均質の場合と比較して C が減少しても、分化による (B − A) の減少は補償されません。したがって、MOI が小さいほど (絶対的な) 秤動振幅が小さくなります。Hussmann ら (2006) の 2 層内部の場合、均質の場合と比較して秤動振幅が減少する範囲は、約 0.5 m (Oberon) から約 13 m (Miranda) です (表 5 (最後の列) を参照)。これらの違いから、均質な固体と分化した固体を区別するために秤動測定で必要な桁数がわかります。これは、内部に海がある可能性が低いミランダに最も関係します (Hussmann et al., 2006; Biersonと Nimmo, 2022; Castillo-Rogez et al., 2023)。
固体衛星が弾性で変形可能な場合、重力トルクは静的膨らみだけでなく、周期的な潮汐膨らみにも作用します。さらに、トルクに対する衛星の応答は、回転速度の変化に対する抵抗を変える潮汐だけでなく、回転速度の変化自体によって引き起こされる変形によっても変化します。完全に固体で弾性のある同期衛星の強制日周振動の振幅は、次のように表されます (例: Van Hoolst et al. (2013))。


表 5: 固体の場合の秤動振幅。列 2 から 5 は、均質体 (MOI 0.4) の自由秤動周期、剛性および弾性振幅、およびそれらの相対差を示します。列 6 から 8 は、Hussmann ら (2006) で定義された 2 層内部 (MOI < 0.4) の剛性および弾性振幅とその差を示します。
最後の列は、均質内部と 2 層内部の固体振幅の差を示します。
ここで、kf は、たとえば Van Hoolst ら (2008) の式 (A3) から MOI の関数として得られる流体ラブ数 (均質体の場合 kf = 3/2)、k2 は古典的な動的ラブ数 (セクション 2.5 を参照) です。一般に、弾性変形は、剛性の場合と比較して、強制日周秤動の (絶対) 振幅を減少させる傾向があります。固体とみなされる大型の氷衛星の場合、減少は限定的である(ガニメデでは約 7%、エウロパでは約 1%、Van Hoolst 他 (2013) を参照)。天王星の小型/中型衛星の場合、均質内部と 2 層内部の両方で差は約 1% 未満である(表 5 を参照)。
3.2.2. 海洋の場合
シェルと固体内部(ここでは岩石コア)の日周振動の振幅は、剛性固体層の場合は Baland と Van Hoolst (2010) の式 (74-75) で、弾性層の場合は Van Hoolst 他 (2013) の式 (62-63) で与えられる。シェルとコアの振動の振幅をそれぞれ gs と gc とする。 Baland と Van Hoolst (2010) は、桁違いの解析により gs の解を近似し、比較的薄いシェルに有効な式 (式 81) を得ました。このアプローチをより厚いシェルに一般化すると、次の式が得られます。

4. 結論
天王星の 5 つの最大の衛星の日周振動の振幅と傾斜角を計算し、回転観測によってそれらの内部を制約できる可能性を評価しました。静水圧平衡を仮定して、まず 3 層内部 (殻、海洋、コア) の範囲を定義し、潮汐ラブ数 k2 も計算しました。
3 層内部の範囲は、Castillo-Rogez ら (2023) の 2 層内部の範囲を保守的に拡張したもので、たとえば外殻と海洋の密度のコントラストを許容しています。ミランダを除く 5 つの衛星すべてについて、MOI の精度 ±0.005 は水圏の厚さの精度が 50 km 以下であることに対応し、CastilloRogez ら (2023) と一致していることがわかりました (セクション 2.3 を参照)。しかし、MOI の精度 ±0.005 は、ミランダの水圏の厚さに関する不確実性約 30 km に相当し、Castillo-Rogez ら (2023) で報告された値の 2 倍であることがわかりました。均質な内部 (MOI = 0.4 に相当) を除外した場合の見通しはわずかに良好で、0.4 と実際の値の差の半分未満の精度で十分です。静水圧平衡を想定すると、MOI の目標精度は、ラダウ方程式を使用して、重力係数 J2 および C22 の目標精度に変換できます。氷殻の厚さに応じて、全球地下海洋を持つ衛星のラブ数 k2 は、分化した完全な固体のラブ数 k2 の 2 ~ 20 倍になります (セクション 2.5 を参照)。均質の場合の値は、3 層の場合の最低値に似ています。したがって、潮汐ラブ数 k2 は、地下海の存在を示す良い指標となり得る。たとえば、分化を仮定し、氷殻の厚さに応じて、k2 の測定精度が 0.003 ~ 0.017 であれば、アリエルに全球的な海があることを検出できる。このような精度は、10 回のフライバイから推定されたタイタンの k2 が 0.06 の精度であることと比較すると、達成が困難であるように思われる (Goossens et al. 2024)。ただし、UOP 宇宙船によるアリエルのフライバイのジオメトリに応じて、0.010 ~ 0.015 の精度が達成される可能性がある (Filice et al., 2024)。暫定的な UOP 10 年ツアーには、高度 25 km (半径の 4%) でのアリエルへの 12 回の近接フライバイが含まれている (Simon et al.)。 (2021) 一方、カッシーニによるタイタンのフライバイは高度 1500 km 超で行われました (半径の 60%)。
天王星の衛星が 2 層の固体であれば、その秤動振幅は
オベロンで約 1 m、ミランダで約 50 m の範囲になります (セクション 3.2.1 を参照)。均質な固体と分化した固体を区別するには、オベロンで約 0.25 m、ミランダで約 6 m の測定精度が必要になります (セクション 3.2.2 を参照)。内部に全球海洋が存在する場合、分化した固体の場合よりも大きな秤動振幅が見つかりました。
ただし、固体の場合と海洋の場合の範囲は重なり合っているため、MOI に独立した制約がないと、秤動測定を使用して海洋を検出することは困難です。もしその MOI が、重力場または形状の正確な測定から数パーセントまでわかっていて、その殻の厚さが 150 km だとしたら、アリエルの海を検出するには、約 5 m の秤動推定精度が必要になります。殻の厚さを制限するには、さらに正確な測定が必要になります。参考までに、カッシーニの画像システムで測定されたミマスとエンケラドゥスの秤動精度は、1 分角 (または表面で 60 m、Tajeddine ら 2014 年、Thomas ら 2016 年) のオーダーです。狭角カメラと広角カメラの最先端の解像度が 2 インチであると仮定すると、Filice らは、 (2024) は、UOP フライバイの形状とフライバイごとにカメラで観測されるランドマークの数に応じて、アリエルの秤動振幅の精度が 0.5 ~ 15 m の範囲にあることを発見しました。潮汐変形は、固体層が硬い場合と比較して秤動振幅を減少させる効果がありますが、その効果は小型および中型の氷衛星では限られています (ミランダの場合は 2% 未満、約 10% 未満)。Nimmo (2023)、Hemingway および Nimmo (2024) で報告された最大値と比較すると、私たちの秤動値は比較的小さいです。これらの低い振幅は主に、Castillo-Rogez ら (2023) が海が存在する場合、その厚さは 50 km 以下であると考えているため、ここでは薄い殻を持つ内部モデルを考慮していないという事実によって説明されます。ranging from 0.2 to 5 m on the obliquity of Ariel, それでも、Nimmo (2023)、Hemingway と Nimmo (2024) が行ったように、より薄いシェルを考慮すると、図 1 (変形可能な固体層) と S6 (剛性固体層) で示されているように、厚いシェルよりも振動の値が大きいことがわかります。しかし、弾性変形を考慮すると振動振幅がわずかに小さくなるという彼らの主張には同意しません。周期的変形がある場合とない場合の海洋ケースを比較すると、振動振幅は完全に固体の場合の値をはるかに上回っていますが、厚さ 10 km の薄いシェルの場合、Ariel と Umbriel、または Titania と Oberon ではそれぞれ約 45% または 65% 減少しています (図 18 を参照)。図が厚いシェルよりも振動振幅が大きいため、振動振幅はより大きくなります。 Hemingway と Nimmo (2024) の S1 と S6 では、数桁にわたる対数スケールが使用されているため、この縮小を視覚化することはより困難です。変形の影響は、ミランダ (5%) のみに限定されています。これらの結果は、マグマの海を持つイオと地下の液体の海を持つエウロパの秤動振幅がそれぞれ 50% と 90% 減少したことと一致しています (Van Hoolst 他、2020、2013)。相互の重力相互作用により、天王星の衛星の軌道と赤道面は、一定の速度で歳差運動せず、傾斜と傾斜角も一定ではありません。ミランダだけが、他の衛星から隔離された物体のように歳差運動し、傾斜角と傾斜角はほぼ一定です。まず、URA111エフェメリスに永年摂動法を適用し、傾斜角振幅で特徴付けられる衛星軌道歳差運動系列を取得しました。付録Aセクションを参照してください。次に、カッシーニ状態モデルを使用して対応する傾斜角振幅を計算しました。強制および自由歳差運動周波数の値に応じて、傾斜角振幅は傾斜角振幅と同じまたは反対の符号になります。共鳴増幅は、自由周波数と強制周波数が互いに近い場合に発生します。均質固体衛星の傾斜角は、2層固体の傾斜角よりも小さくなります。たとえば、固体ミランダの均質ケースを除外するには、表面で約8mの測定精度が必要になります。セクション3.3.1を参照してください。Filice et al. (2024) は、UOP フライバイの形状とフライバイごとにカメラで観測されるランドマークの数に応じて、アリエルの傾斜角の精度が 0.2 ~ 5 m の範囲にあることを発見しましたが、1.3 m の精度が必要になります。内部に全球海洋が存在する場合、カッシーニ状態モデルは 3 つの自由モード (FP、FON、FIN) によって特徴付けられ、5 つの衛星で共鳴増幅が発生します (ミランダの場合は非常に薄い海洋がある内部のみ)。セクション 3.3.2 を参照してください。非共鳴状態では、シェル傾斜角の値はすべて、固体に予想される範囲内にほぼ収まるため、傾斜角測定から海洋を検出することは困難と思われます。衛星が共鳴状態にあることが判明した場合、海洋の存在は依然として確認できます。潮汐変形は固体層が硬い場合と比較して傾斜角を増大させる効果がありますが、天王星の小型および中型の氷衛星ではその効果は限定的です (ミランダでは 0.5% 未満、チタニアとオベロンでは最大 10%)。ここで提示した結果は、文献で時折報告される推論と矛盾しています。その推論では、氷衛星の氷殻は固体内部から機械的に分離されており、固体の場合よりも大きな傾斜角である程度独立して歳差運動すると想定されています (例: Bills および Nimmo (2008)、Chen 他 (2014)、Nimmo (2023))。この推論は、非共鳴状態であっても、回転の短い時間スケールで氷殻が固体内部からある程度独立して歳差運動するという日周秤動との類似性に基づいています。しかし、内部に液体層があり、共鳴領域外にある場合、スピン軌道共鳴状態にある物体の表面層の傾斜は固体の傾斜に近くなります。これは、歳差運動の長い時間スケールでは、物体がほぼ固体のように振舞うためです (水星については Baland (2022) とその中の参考文献、エウロパについては Coyette ら (2022) も参照)。
我々の結果は、海洋の検出や内部の制限に必要な測定精度に関する解釈に大きな影響を与えないと考えられる特定の仮定に基づいています。
たとえば、天王星の最大の衛星は、静水圧平衡からわずかに逸脱している可能性があります。ここで使用する軌道歳差の永年モデルは、軌道歳差の記述に誤差をもたらし、それが自転歳差の記述に伝播します。UOP ミッションで衛星の回転が測定される場合、静水圧平衡から逸脱する内部モデル (エンケラドゥスで行われたように、たとえば Van Hoolst ら (2016)) と、これらの測定値を解釈するためのより正確な軌道モデルを考慮する必要があるかもしれません。
この研究では、天王星の 5 つの最大の衛星の内部を制限するために、秤動、傾斜角、およびそれほどではないが潮汐測定の可能性を個別に説明しました。静重力場の推定値と潮汐力および回転力の測定を組み合わせることで、内部構造(さまざまな層のサイズ、密度、剛性)を特徴付けることができるはずです。これについては、マルコフ連鎖モンテカルロ(MCMC)アプローチを使用して天王星の衛星の内部特性を推測する関連論文でさらに詳しく説明しています。この後続の研究では、ターゲット測定の精度が計算され、UOPミッションの改良と定義に役立つ貴重な入力が提供されます(Filice et al.(2024)を参照)。
天王星の最大の衛星の秤動と黄道傾斜角
要約
太陽系で複数の海洋世界が発見され、2023~2032年の惑星科学および宇宙生物学10年計画で天王星が最優先目標に選ばれたことを受けて、天王星の5つの最大の衛星(ミランダ、アリエル、ウンブリエル、チタニア、オベロン)も地下海が存在する可能性があるため、新たな注目を集めています。私たちは、自転測定が天体の内部分化の確認や内部海の存在の検出にどのように役立つかを評価します。天王星の同期衛星の平坦な形状に対する時間的に変化する重力トルクにより、衛星は平均自転に対して秤動し、黄道傾斜角がゼロではない状態で歳差運動します。岩石の核を水圏で囲んだ固体または外側の氷の殻に分かれ、その下に液体の海があるさまざまな内部モデルについて、日周の秤動振幅と傾斜角を計算します。天王星の衛星が 2 層の固体であれば、オベロンの約 0.25 m からミランダの約 6 m までの秤動測定精度から、均質な内部空間が存在する可能性は排除されます。平均慣性モーメント (MOI) の独立した推定値と組み合わせることで、秤動測定を使用して海の存在を検出することもできますが、これに必要な測定精度は、秤動振幅の実際の値によって異なります。傾斜角を計算するには、まず永年摂動モデルを使用して、5 つの衛星すべての軌道歳差運動の系列を作成します。ミランダを除いて、衛星間の重力相互作用により、天王星の大型衛星の傾斜角は平均値の周りで比較的大きな周期的変動を示すことが示されています。アリエルの約 1 メートルからオベロンの約 400 メートルまでの傾斜角測定精度により、均質なケースを除外できることがわかっています。地球内部の海洋の存在により、傾斜角の共鳴増幅が可能になり、検出が容易になります。このような共鳴が発生しない場合、傾斜角は固体の場合とほとんど区別がつかなくなります。潮汐変形が小型から中型の天王星の衛星の自転に与える影響は限られていることが示されています。ティタニアとオベロンでは、秤動が最大 10% 減少し、傾斜角が最大 15% 増加しますが、ミランダではその影響は無視できます。
1. はじめに
ミランダ、アリエル、ウンブリエル、ティタニア、オベロンは、英語文学の登場人物にちなんで名付けられた天王星の 5 つの最大の衛星です。これらは小型または中型の氷衛星で、まだほとんど何もわかっていません。ウィリアム ハーシェル (ティタニアとオベロン、1787 年)、ウィリアム ラッセル (アリエルとウンブリエル、1851 年)、ジェラルド カイパー (ミランダ、1948 年) によって発見されましたが、1986 年にボイジャー 2 号が天王星をフライバイした際に、宇宙探査ミッションによって一度だけ訪問されました。
過去数十年間で、太陽系の外縁部、木星と土星の氷衛星の表面下で水が液体の状態で存在できることがわかっています (Nimmo と Pappalardo、2016 年)。ガリレオ計画は木星の衛星システムを広範囲に調査し、エウロパ、ガニメデ、カリスト付近で誘導磁場を発見し、地下海の存在を示唆しました (Khurana 他、1998 年、Kivelson 他、2002 年)。磁気誘導は、これらの海を検出するための複数の手法の 1 つにすぎません。エウロパとその「氷山」の場合のように、表面を観察すると刺激的なことがあります (Carr 他、1998 年)。最近のハッブル宇宙望遠鏡 (HST) によるガニメデのオーロラオーバルの低振幅振動の観測は、厚い氷の層の下に地下海が存在することを示しています (Saur 他、2015 年)。カッシーニ計画は、氷の衛星の地下海を検出するために使用される手法の範囲を拡大しました。小型のエンケラドゥスは異常に暖かい南極で異常な活動を示し、水蒸気と氷粒子の噴出は、地表の下に液体の水があり、その下にある岩石の核と接触している証拠であると解釈されています (Porco et al., 2006; Spencer et al., 2006, 2009; Postberg et al., 2011)。エンケラドゥスの形状、重力場、日周振動は、厚さ約 20 ~ 30 km の氷殻の下に地球規模の水の貯留層があることと一致しています (Park et al. (2024) およびそこに記載されている参考文献)。ディオネの重力と形状は、地球規模の水の海を覆う氷殻の観点からも説明できます (Beuthe et al., 2016; Zannoni et al., 2020)。観測されたタイタンの傾斜角は、完全に固体で硬いタイタンに予想される傾斜角の約 3 倍です (Baland 他 (2019) およびその中の参考文献)。衛星が経験した大きな日周潮汐変形も、タイタン内部に地球規模の海が存在することを証明しています (Iess 他、2012 年、Durante 他、2019 年、Goossens 他、2024 年)。一方、地球規模の海を覆う厚い氷の殻は、ホイヘンス探査機による電場測定を説明しています (B´eghin 他、2012 年)。海を持つ氷衛星のクラブに最近加わったのは、多数のクレーターがあるミマスかもしれません。その秤動は深部に液体層が存在することと一致する可能性があり(Tajeddine et al., 2014)、軌道の進化は地表から20〜30 kmの深さに非常に若い海が存在することを示唆している(Lainey)。ボイジャー、ガリレオ、カッシーニ・ホイヘンスはフラッグシップクラスのミッションでした。海王星、天王星、およびそれらの衛星は、野心的な探査ミッションをまだ待っています。天王星探査機(UOP)は、2023〜2033年の惑星科学および宇宙生物学10年調査(米国科学、工学、医学アカデミー、2023年)によって、次のフラッグシップクラスのミッションとして優先されています。とりわけ、このミッションは、4年間のツアー中に、5つの最大の衛星に関する重要な質問に取り組むことを目指します。それらの岩石と氷の質量比と内部構造は?どの衛星に内部海があるか?これらの質問への答えは、それらの形成と進化を制限するのにも役立ちます。
この論文では、将来のUOP宇宙船のペイロードの一部となる狭角カメラと広角カメラ(NACとWAC)で取得した画像からランドマーク追跡などの手法で推定できる、天王星最大の衛星の回転観測可能範囲(秤動と黄道傾斜)を定義することを目的としています。光学データは、宇宙船に搭載された無線科学実験の放射測定データと併用して、衛星の内部を推測することができます(Filice et al.、2024)。この研究では考慮されていませんが、磁気誘導も、天王星の最大の衛星内の地下海を調査するために提案されています(例:Cochrane et al.(2021)。
この論文は次のように構成されています。セクション 2 では、既存の文献に基づいて、各衛星の 3 層内部 (シェル、海洋、コア) の範囲を定義し、静水圧平衡にあると想定します。内部は質量と半径によって制約され、総平均慣性モーメント (MOI) と次数 2 の重力係数、および各層の密度、寸法、平坦度によって特徴付けられます。以前の研究では、海洋と氷殻の密度の違いの影響は調査されていませんでした。これが、水圏の厚さやグローバルな差異の観点から推定された MOI と重力係数の解釈にどのように影響するかについて簡単に説明します。セクション 3 では、衛星がカッシーニ状態に固定されていると想定して、セクション 2 で定義した 3 層内部の固体層 (シェルとコア) の日周振動の振幅と傾斜角を計算します。回転測定に必要な精度について議論し、これらの測定を内部特性や全体的差異の観点から解釈できるようにします。結論はセクション 4 で示し、私たちの秤動測定結果と Hemingway と Nimmo (2024) による最近の研究との類似点と相違点について議論します。
2. 衛星の内部と重力場
2.1. 質量、半径、平均密度
天王星の 5 つの最大の衛星の内部に関する主な観測上の制約は、質量と半径です (表 1 を参照)。地球ベースの天体測定、ボイジャー 2 号の観測、および Jacobson (2014) によるリング掩蔽から、それらの軌道と質量を決定しました。リム座標から 5 つの衛星の形状と半径の推定は、ボイジャー 2 号の時代にまで遡ります (Thomas、1988)。恒星掩蔽解析に基づくウンブリエルの平均半径の最新値は、Assafin et al. (2023) で報告されていますが、統計的には以前の推定値と変わりません。質量と半径から得られた密度と表面の観測結果を組み合わせると、衛星の構成と内部構造に関する最初の兆候が得られます。アリエル、ウンブリエル、チタニア、オベロンは中型の衛星で、密度が低いことから内部は主に水氷でできていることがわかります。一方、ミランダはエンケラドゥスやミマスのような小型衛星ですが、密度が低く、したがって岩石と氷の比率も低くなっています (Hussmann et al., 2006)。

表 1: 天王星の 5 つの大きな衛星の赤道半径と極半径 (a > b > c)、平均半径 R、重力パラメータ GM、平均密度 ¯ρ。Thomas (1988) および Jacobson (2014) による。
2.2. 慣性モーメントと重力場
正規化された平均慣性モーメント MOI = I/MR^2
は内部分化の指標であり、天王星の衛星についてはまだ決定されていません。約 0.3 から 0.4 の間で変化すると考えられます (たとえば、分化の観点から 2 つの端の要素であるガニメデとカリストではそれぞれ 0.31 と 0.36、(Schubert ら、2004))。

図 1: 天王星の衛星の非正規化重力係数 J2 と C22 を、静水圧平衡を仮定して式 (1) から計算した、正規化平均慣性モーメント I/MR^2 の関数として表したもの。点は、Chen ら (2014) の C/MR^2 (ここでは I/MR^2 の代理として採用) = 0.33 の値を示しています。灰色の破線は、ディオネの推定値 (Zannoni ら、2020) を示しています。静水圧平衡を仮定すると、重力場の係数 J2 と C22 の値は、I/MR^2 の任意の値に対して、ラダウの方程式と J2 と C22 の静水圧関係 (例: Van Hoolst ら (2008)) から取得できます。

ここで、qr = n^2R^3/GM は遠心加速度と重力加速度の比で、n は平均運動、R は平均半径、GM は重力パラメータです。注意:
Radau の式は、次数 2 の重力係数を、文献でよく見られる極慣性モーメント (C/MR^2 = I/MR^2 + 2J2/3) ではなく、正規化された平均慣性モーメント (I/MR^2) に関連付けます (例: Castillo-Rogez ら (2023) の式 7)。Van Hoolst ら (2008) の式 (47) の後の議論を参照してください)。図 1 は、5 つの衛星の J2 および C22 範囲を I/MR^2 の関数として示しています。ここでは、同じ仮説に基づく以前の推定値 (Chen et al., 2014; Castillo-Rogez et al.,2023) と一致する値を得ています。これらの計算は、主に桁数を特定することを目的としています。衛星の内部構造や、衛星が何層に分割されているかについての仮定は必要ありません。このようにして得られた桁数は、土星の衛星でアリエルやウンブリエルとほぼ同じ大きさのディオネの重力係数と一致しますが、ディオネは静水圧平衡を満たさないことが知られています (Zannoni et al., 2020)。ミランダとアリエルの楕円形 (a > b > c) は、Thomas (1988) によって推定されました。ボイジャー2号が衛星を部分的にカバーしたことを考えると、これらの形状が静水圧平衡仮説と一致するかどうかを確実に結論付けることは困難であり、おそらくa、b、cに関する形式的な不確実性が小さいことはいくぶん楽観的である。Castillo-Rogez et al. (2023)と同様に、a、b、cの個々の値は静水圧平衡に期待される値と一致することがわかった(図2を参照)。Castillo-Rogez et al. (2023)とは異なり、(b − c)/(a − c)の組み合わせ(ミランダとアリエルの場合はそれぞれ0.17 ± 0.17と0.06 ± 0.33)も、期待される静水圧値0.25と一致することがわかった。明確な反証が得られるまでは、以下に示すように、天王星の大型衛星の回転をモデル化する際に、これらの衛星が静水圧平衡にあると仮定するのが妥当である。

図 2: ミランダとアリエルの赤道半径と極半径 (a > b > c) を MOI (I/MR2) の関数として表したもの。Van Hoolst ら (2008) の式 (35) で定義され、式 (3) と平均半径 R = (a+b+c)/3 から計算され、静水圧平衡 (実線) を仮定しています。網掛け部分は Thomas (1988) による 1σ の推定値に対応しています。
2.3. 3 層内部
Hussmann ら (2006)、Bierson と Nimmo (2022)、Castillo-Rogez ら (2023) に従い、ここでは衛星がすべて岩石コアと外部水圏に分化していると仮定します。
水圏は、完全に氷 I マントルであるか、氷 I 殻と岩石核に接する液体の水の海に分かれています。 Hussmann ら (2006)、Bierson と Nimmo (2022)、Castillo-Rogez ら (2023) は、液体の海の可能性について異なる結論に達しています。 Hussmann ら (2006) と Bierson と Nimmo (2022) によると、水の海は少なくとも 100 km の厚さの氷殻の下にある Titania と Oberon でのみ可能です。 Castillo-Rogez ら (2023) は、厚い (> 200 km) 氷殻の下にある、Ariel と Umbriel では 30 km 未満の厚さの深海、Titania と Oberon では 50 km 未満の深海が残ると予測しています。ビアソンとニモ(2022)は、カスティーヨ・ロジェスら(2023)とは対照的に、他の衛星の海洋を維持するのに役立つ可能性のある潮汐加熱を無視するという保守的なアプローチを採用していることに留意すべきである。ミランダの衛星は非常に小さく、潮汐共鳴の外では、わずか数十億年で海洋が凍結するため、ミランダの地下海洋の可能性はすべて排除されている。この探索的研究では、2層または3層の密度と寸法について比較的保守的な範囲を検討し、これらのパラメータが自転に与える影響を説明することを目指している。その精神で、ミランダには液体の海洋が存在する可能性もあると考えている。氷と水の密度範囲は広く(700~1050 kg m−3、最も低い密度は多孔性が高いことを意味し、最も高い密度はアンモニアや塩などの不純物が存在することを意味する)、Castillo-Rogez ら(2023)がセクション 6.1 で水圏に使用した範囲に従います。これらの著者とは異なり、ここでは水と氷の間の可変密度コントラスト(ρo ≥ ρs)の影響を検討します。岩石の密度範囲は、Hussmann ら(2006)や Bierson と Nimmo(2022)と同様に、2400 kg m^−3(Castillo-Rogez ら(2023)の最小値)から 3500 kg m−3 までです。Castillo-Rogez らに従い、海の厚さは最大 50 km と見なします。 (2023)。
3層内部のセットを構築するには、まず海洋の厚さhoを2.5~50 kmに設定し、次に氷、水、岩石の密度と総半径および質量の制約から氷殻の厚さhsと岩石コアの半径Rc = R − hs − hoを導き出します。海洋の厚さは制限されている(ho ≤ 50 km)ように選択されているため、氷殻は5つの衛星すべてで比較的厚くなります(ミランダの場合はhs ≳ 30 km、その他の衛星の場合はhs ≳ 70 km、表2を参照)。3層内部のMOIは(例:Van Hoolst et al. 2008)で与えられ、

Ro = R − hs、平均海洋半径です。差別化された内部のセットのMOIと重力係数の範囲は、均質な物体の値よりも小さくなります。この研究では、圧力が物質の密度に与える影響を無視しているため、組成に関して完全に均質な物体は密度が均一で、MOI は 0.4 になります。

表 2: 本研究で回転観測量の計算に考慮した天王星衛星内部の 3 層の密度と寸法の範囲。総 MOI の範囲と次数 2 の重力係数 J2 と C22 も示し、同じ質量と半径の均質衛星の値と比較します。
私たちの 3 層内部範囲は基本的に Castillo-Rogez ら (2023) の 2 層内部範囲の保守的な拡張であるため、ここでは将来のミッションの観測量としての MOI と C22 に関するセクション 6.1 で開始された議論を続けます。C22 は宇宙ミッションで実施された電波科学実験の古典的な結果ですが、MOI は静水力学的仮定が適用される場合、ラダウ方程式を使用して C22 から導き出すことができます (セクション 2.2 を参照)。
Castillo-Rogez らの図 11 に示されている MOI と岩石コア密度および水圏の厚さの関係は、Castillo-Rogez らの図 12 で示されています。 (2023) は、岩石コアと水圏を持つ 2 層モデルに関するものです。これらの 2 層モデルは、質量分布の点で、殻と海洋の密度が等しい 3 層モデルと同一です。図 3 では、殻と海洋の密度差も含む 3 層内部の MOI と ρc および hs + ho の関係を示しています。氷と水の密度に対する制約が限られているため、MOI から内部を制約できる可能性は疑問です。Castillo-Rogez ら (2023) と同様に、ここでは将来の MOI 決定の精度を ±0.005 と見なしています。これは約 1.5% の誤差に相当し、エンケラドゥスやディオネなどの小さな氷衛星の重力場決定の実際の精度を考えると妥当と思われます (Iess ら、2012 年、Zannini ら、2020 年)。ここで、岩石密度と殻と海洋の密度の対比について考慮した保守的な範囲では、MOI の精度 ±0.005 は、ミランダの水圏の厚さの不確実性約 30 km に相当します (Castillo-Rogez ら (2023) で報告された 15 km に対して)。また、殻の密度が 50 kg/m3 よりも高い精度で決定されたとしても、海洋の密度は小さい ρs に対して本質的に制約を受けません。中型衛星の Ariel、Umbriel、Titania、Oberon の場合、MOI の精度 ±0.005 は、Castillo-Rogez ら (2023) ですでに示されているように、水圏の厚さの不確実性 50 km に相当します。ミランダの場合と同様に、ここで行っているように、より高い最大コア密度を考慮すると、特定の MOI に対して許容される水圏の厚さの範囲が広がる傾向があることに注意してください。内部パラメータ、つまり氷水/岩石比を決定できない場合、物体が均質であるか分化しているかを少なくとも決定することはできるでしょうか。これは、Castillo-Rogez ら (2023) が MOI の関数として C22 の図 12 で取り上げている問題です。まず、静水圧平衡を仮定すると、MOI 情報は C22 情報と完全に同等であることを指摘したいと思います。Castillo-Rogez ら (2023) の図 12 は、図 1 に示すように詳細な内部構造に依存しない Radau の関係を示しています。したがって、ここでは MOI に焦点を当てて議論します。MOI に必要な精度は、均質な対応値 0.40 に対するパラメータの実際の値に依存します。Miranda を除いて、すべての MOI 値は、岩石密度が低い場合でも 0.34 未満です。 MOI 値が低いほど、均質な物体と分化した物体を区別しやすくなります。値が 0.4 に近いほど、測定の精度が高くなるためです。たとえば、Oberon の MOI が 0.34 の場合、分化した内部と均質な内部を区別するには、0.06 以下の精度が必要です。Miranda の MOI が 0.29 の場合、0.11 未満の精度で十分です。C22 では、それぞれ 0.8 × 10−5 と 170 × 10−5 の精度になります。
2.4. 平坦化
静水圧平衡にある 3 層の同期衛星の回転をモデル化するには、その層の慣性モーメントを計算する必要があります。これは、表面の極 (α) および赤道 (β) の平坦化と、殻と海洋、海洋とコアの楕円体界面の平坦化に依存します。この論文の残りの部分では、下付き文字 s、o、c は、それぞれ表面、海洋半径、コア半径の平坦化を表します。同期衛星は、回転と静潮の両方によって平坦化されます。表面の極 (αs) および赤道 (βs) の平坦化は、次のように定義されます (Van Hoolst et al.、2008)
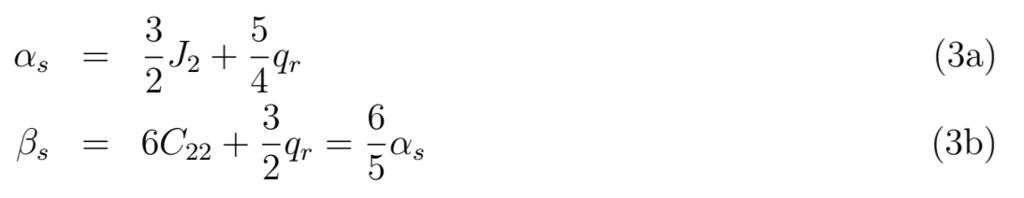
したがって、重力係数を通じて MOI と一義的に関連しています。極および/または赤道幾何学的平坦化を J2 および C22 重力係数よりも正確に測定できれば、ラダウ方程式を使用して MOI を導くために使用できます。海洋半径 Ro (αo、βo) およびコア半径 Rc (αc、βc) での平坦化は、クレローの微分方程式を積分することによって得られます。関係 β = 6α/5 は、どの深さでも有効です (詳細は Van Hoolst ら (2008) を参照)。
図 4 の右パネルは、ミランダの場合の極平坦化と深さの関係を示しています。端メンバー 3 層内部の密度プロファイルは左パネルに示されています。
中心から表面に向かって α が増加することがわかります。αs は MOI の減少とともに減少し、したがってシェル密度 ρs の減少とともに減少する傾向があります。シェルと海洋の密度のコントラストもシェルの平坦化に影響する可能性があります (特に MOI が大きい場合) が、考慮される最小および最大 MOI によって許容される範囲内に常に留まります。

図 3: 表 2 で定義される、3 層のミランダ、アリエル (ウンブリエルの代理)、チタニア (オベロンの代理) の岩石コア密度 ρc (左パネル) と水圏の厚さ hs + ho (右パネル) の関数としての MOI。この図は、Castillo-Rogez ら (2023) の図 11 に基づいています。線は、下から上に向かって、50 kg/m3 刻みで ρs = 700 kg/m^3 から 1050 kg/m^3 に対応しています (実線と破線の場合はそれぞれ ρo = ρs と ρo = 1050 kg/m3)。破線は、固定された海洋の厚さ ho = 50 km にも対応しており、密度のコントラストが MOI に及ぼす最大の影響を示しています。
2.5。潮汐ラブ数 k2
天王星の重力場は衛星の周期的な変形の原因であり、その結果、衛星の重力ポテンシャルの周期的な変動が潮汐ラブ数 k2 に比例します。k2 値が小さいということは、変形がほとんどないかなり硬い物体であることを示します。同期衛星の回転は潮汐変形に依存します。周期的な変形の膨らみがさまざまな層で発生する結合に影響を与えるためです。周期的な潮汐変形が大型衛星の回転に与える影響は非常に重要になる場合がありますが (秤動については Van Hoolst 他 (2013) を参照)、エンケラドゥスのような小型衛星では影響は小さくなります (Van Hoolst 他、2016 年、Baland 他、

図 4: ミランダの密度 (左) と極の平坦化 (右) を半径の関数として、最小 (青の実線: ρs = ρo = 700 kg/m^3、ρc = 3500 kg/m^3、ho = 50 km) および最大 (オレンジの実線:ρs = ρo = 1050 kg/m^3、ρc = 2400 kg/m^3、ho = 2.5 km) の MOI を持つ内部で示しています。破線の青とオレンジの線は、同様の内部に対応していますが、それぞれ ρo = 1050 kg/m^3 と ρs = 700 kg/m^3です。
2016)。したがって、ミランダでも小さく、中型の天王星の衛星ではやや大きくなると予想されます。弾性効果は第 3 章で秤動に及ぼす影響を定量化します。
2 層体について Hussmann ら (2006) が報告した値を含む k2 の範囲と、3 層モデルで得た結果を検討し、海洋の有無にかかわらず、潮汐変形が回転に及ぼす影響の可能性について議論します。粘性の影響については、天王星の衛星のラブ数の詳細な計算が目的ではないため、ここでは取り上げません。
剛性 µ の均質体の場合、潮汐ラブ数は次のように表すことができます。Melchior(1973)

天王星の衛星の値は、表 3 の 2 番目の列に示されており、µ = 4×10^9 Pa (純粋な氷を最もよく表す値) です。これは Chen ら (2014) の値と一致しています。2 層の固体の場合、k2 のコア半径 (または同等の氷マントルの厚さ) への依存性は絶対値では小さいです。したがって、Hussmann ら (2006) によって提供され、表 3 の 3 番目の列に報告されている固有の値のみを考慮します。液体の海を持つ 3 層の物体の場合、標準的なプロパゲーター マトリックス手法 (例: Sabadini ら (2016)) を使用します。Hussmann ら (2006) に従い、シェルとコアの剛性としてそれぞれ µs = 3.3×10^9 Pa、µc = 50×10^9 Pa を使用します。 ρs = ρo の場合、Beuthe (2015) の均質地殻モデル (付録 A を参照) は、標準モデルと比較して約 1% の精度です。均質地殻モデルはコアの半径と密度に明示的に依存しないため、これらのパラメータに関連して大きく変化しない標準モデルで得られた結果に光を当てます。一般モデルで得られた範囲は、表 3 の列 4 に示されています。3 層の k2 は、以前のモデルに全球の地下海洋が含まれているため、2 層の k2 の 2 ~ 20 倍大きくなりますが、均質ケースの値は 3 層ケースの最低値に似ています。 3層の場合、図5に示すように、シェルの厚さhsが減少するにつれてk2が増加します。
k2は、ミランダでは約0.004、アリエルとウンブリエルでは0.035、チタニアとオベロンでは0.07まで大きくなります。最低値(ミランダでは約0.0008、アリエルとウンブリエルでは0.008、オベロンでは0.016)は、後者の場合、剛性を考慮した結果として、k2 は均質の場合に近くなります。k2 は、氷の剛性と氷および海洋の密度に依存しますが、その程度は均質の場合より低くなります。剛性が減少すると、k2 は増加します (ここでは示されていません)。シェルと海洋の密度が高いほど、潮汐ラブ数が大きくなることが予想されますが、密度の高いシェルと海洋は質量制約を満たすためにシェルが厚くなることを意味し、これにより、内部モデル セットでの k2 の増加が緩和されることに留意する必要があります。

表 3: 各衛星のラブ数 k2。固体均質ケース (2 番目の列)、固体 2 層ケース (3 番目の列 - Hussmann ら (2006) の値)、および液体の海がある 3 層ケース (最後の列)。

図 5: 表 2 で定義される 3 層内部の氷殻厚さ hs の関数としてのラブ数 k2。
色付きの実線は、ρo = ρs の場合に対応します (値はカラー コードで示されます)。色付きの破線は、同じ殻密度と ρo = 1050 kg/m^3 の場合に対応します。黒の実線と破線は、表 3 で報告されている 2 層および均質固体の場合に対応します。
3. 自転
天王星の赤道は、その軌道面に対してほぼ直角です。天王星の 5 つの大きな衛星の軌道は、天王星の赤道とほぼ同一平面にあり、離心率は比較的小さいです。傾斜は 0.30 度未満です (傾斜が 4.4 ◦ のミランダを除く)。ボイジャー 2 号が撮影した画像により、これらの衛星は月と同様に同期回転しており、その回転軸は天王星の自転軸とほぼ平行であるという理論上の予想が確認されました (Smith ら、1986 年)。また、これらの衛星は、低傾斜カッシーニ状態に閉じ込められている可能性も高いとされています (Gomes と Correia (2024 年) を参照)。次のサブセクションでは、これらの衛星の強制日周振動と自転歳差運動について調べます。この研究には、ガリレオ衛星、タイタン、エンケラドゥスなどに適用された、以前に公開された回転モデルを使用します。
3.1. 軌道モデル
回転モデルの入力として、URA111 エフェメリス (Jacobson、2014 年) から得られた軌道パラメータを使用します。衛星の軌道を記述するために必要な詳細レベルは、モデル化の目的によって異なります。秤動に関しては、ケプラー軌道上の衛星の回転の変動に対応する日周成分のみをモデル化します。軌道摂動により、他の周期の秤動も存在します。日周秤動は周期が短いため、宇宙ミッション データ内の他の変動とは異なる信号として識別できます (例: Thomas 他 (2016))。また、衛星の内部構造に最も依存するのは回転変動です (長周期の秤動は、内部モードとの共鳴が存在しない限り、内部構造にほとんど依存しません)。日周秤動をモデル化するには、Jacobson (2014) の表 2 に示され、ここで表 4 に再現されている平均軌道離心率 e と平均運動 n のみが関連します。

表 4: 平均軌道離心率 e、平均運動 n、公転周期 (Jacobson、2014)。
スピン歳差運動と傾斜角に関しては、衛星の軌道の説明にはより注意が必要です。衛星の傾斜角とスピン歳差運動は、傾斜角と軌道歳差運動によって決まります。Jacobson (2014) の表 2 にある、時間に依存しない傾斜角と歳差運動率を持つ平均軌道要素は、この文脈では適切な表現ではありません。軌道歳差運動は必ずしも均一ではなく、傾斜角は軌道周期よりもはるかに長い期間にわたって変化します。その結果、傾斜角も長期間にわたって変化します。将来の宇宙船の観測から傾斜角を予測するには、これらの変化をモデル化する必要があります。訪問宇宙船から得られる傾斜角の瞬間値 (または比較的短い期間の平均) に関する情報のみに注意してください (例: Stiles ら (2008))。スピン歳差運動と傾斜角をモデル化するために、永年摂動モデルで構築された軌道歳差運動の系列を使用することにしました。付録
付録 A を参照してください。
3.2. 日周秤動
同期衛星が偏心軌道に沿って公転すると、その長軸が惑星の中心を正確に指していないため、惑星は時間とともに変化する重力トルクを衛星に及ぼし、日周の縦方向秤動を引き起こします (例: Comstock and Bills (2003))。内部海洋またはその他のグローバル流体層が存在する場合、外部重力トルクに対する応答は、衛星の異なる層間の結合によって変化します。日周秤動の振幅は、天体とその層の周期的な変形によっても影響を受けます。
3.2.1. 固体の場合
完全に固体で剛性のある同期衛星の強制日周振動の振幅は、次のように表されます (例: Van Hoolst 他 (2008))
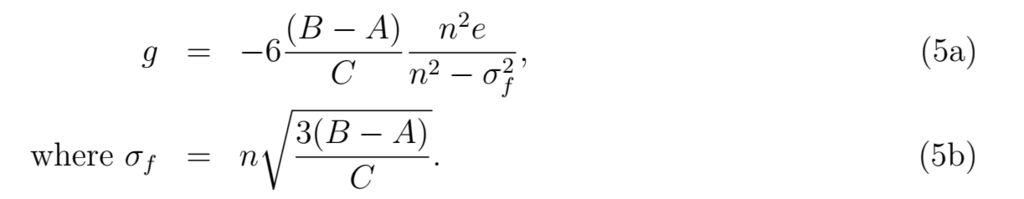
振幅 g は、軌道離心率 e と衛星の赤道慣性モーメントの差 (A < B) に比例し、極慣性モーメント C に反比例します。 (B − A) と e は、親惑星によって及ぼされる重力トルクの強さを表し、C は、加えられたトルクに対する衛星の抵抗を表します。 σf は、自由振動の固有周波数です。固体で剛性のある衛星の振動振幅は、内部構造を特徴付けるさまざまな層の密度とサイズに直接依存せず、主慣性モーメントのみに依存します。したがって、静水圧平衡を仮定すると、ラダウの方程式から、特定の衛星の秤動振幅は MOI のみに依存することがわかります。密度プロファイルが異なるが同じ MOI を持つ 2 つの内部は、同じ秤動振幅を持ちます。天王星の衛星が剛体で均質な物体である場合、その秤動振幅は、表面でオベロンの約 1 m からミランダの 62 m の範囲になります (表 5 を参照)。固体の秤動振幅は、自由周期が強制周期の約 4 (ミランダ) から 45 (オベロン) 倍長く、g ≃ −6e(B − A)/C であるため、共鳴効果がほとんどまたはまったくありません。一般的な規則として、同期衛星が惑星に近いほど、自転速度が速くなり、差 (B − A)/MR2 が大きくなり、秤動振幅が大きくなります。特に大きな離心率を持つ衛星は、この規則に反する可能性があります (たとえば、ウンブリエルの離心率はアリエルのほぼ 4 倍であるため、その秤動振幅も大きくなります)。2 層に分化した天体の場合、均質の場合と比較して C が減少しても、分化による (B − A) の減少は補償されません。したがって、MOI が小さいほど (絶対的な) 秤動振幅が小さくなります。Hussmann ら (2006) の 2 層内部の場合、均質の場合と比較して秤動振幅が減少する範囲は、約 0.5 m (Oberon) から約 13 m (Miranda) です (表 5 (最後の列) を参照)。これらの違いから、均質な固体と分化した固体を区別するために秤動測定で必要な桁数がわかります。これは、内部に海がある可能性が低いミランダに最も関係します (Hussmann et al., 2006; Biersonと Nimmo, 2022; Castillo-Rogez et al., 2023)。
固体衛星が弾性で変形可能な場合、重力トルクは静的膨らみだけでなく、周期的な潮汐膨らみにも作用します。さらに、トルクに対する衛星の応答は、回転速度の変化に対する抵抗を変える潮汐だけでなく、回転速度の変化自体によって引き起こされる変形によっても変化します。完全に固体で弾性のある同期衛星の強制日周振動の振幅は、次のように表されます (例: Van Hoolst et al. (2013))。


表 5: 固体の場合の秤動振幅。列 2 から 5 は、均質体 (MOI 0.4) の自由秤動周期、剛性および弾性振幅、およびそれらの相対差を示します。列 6 から 8 は、Hussmann ら (2006) で定義された 2 層内部 (MOI < 0.4) の剛性および弾性振幅とその差を示します。
最後の列は、均質内部と 2 層内部の固体振幅の差を示します。
ここで、kf は、たとえば Van Hoolst ら (2008) の式 (A3) から MOI の関数として得られる流体ラブ数 (均質体の場合 kf = 3/2)、k2 は古典的な動的ラブ数 (セクション 2.5 を参照) です。一般に、弾性変形は、剛性の場合と比較して、強制日周秤動の (絶対) 振幅を減少させる傾向があります。固体とみなされる大型の氷衛星の場合、減少は限定的である(ガニメデでは約 7%、エウロパでは約 1%、Van Hoolst 他 (2013) を参照)。天王星の小型/中型衛星の場合、均質内部と 2 層内部の両方で差は約 1% 未満である(表 5 を参照)。
3.2.2. 海洋の場合
シェルと固体内部(ここでは岩石コア)の日周振動の振幅は、剛性固体層の場合は Baland と Van Hoolst (2010) の式 (74-75) で、弾性層の場合は Van Hoolst 他 (2013) の式 (62-63) で与えられる。シェルとコアの振動の振幅をそれぞれ gs と gc とする。 Baland と Van Hoolst (2010) は、桁違いの解析により gs の解を近似し、比較的薄いシェルに有効な式 (式 81) を得ました。このアプローチをより厚いシェルに一般化すると、次の式が得られます。

4. 結論
天王星の 5 つの最大の衛星の日周振動の振幅と傾斜角を計算し、回転観測によってそれらの内部を制約できる可能性を評価しました。静水圧平衡を仮定して、まず 3 層内部 (殻、海洋、コア) の範囲を定義し、潮汐ラブ数 k2 も計算しました。
3 層内部の範囲は、Castillo-Rogez ら (2023) の 2 層内部の範囲を保守的に拡張したもので、たとえば外殻と海洋の密度のコントラストを許容しています。ミランダを除く 5 つの衛星すべてについて、MOI の精度 ±0.005 は水圏の厚さの精度が 50 km 以下であることに対応し、CastilloRogez ら (2023) と一致していることがわかりました (セクション 2.3 を参照)。しかし、MOI の精度 ±0.005 は、ミランダの水圏の厚さに関する不確実性約 30 km に相当し、Castillo-Rogez ら (2023) で報告された値の 2 倍であることがわかりました。均質な内部 (MOI = 0.4 に相当) を除外した場合の見通しはわずかに良好で、0.4 と実際の値の差の半分未満の精度で十分です。静水圧平衡を想定すると、MOI の目標精度は、ラダウ方程式を使用して、重力係数 J2 および C22 の目標精度に変換できます。氷殻の厚さに応じて、全球地下海洋を持つ衛星のラブ数 k2 は、分化した完全な固体のラブ数 k2 の 2 ~ 20 倍になります (セクション 2.5 を参照)。均質の場合の値は、3 層の場合の最低値に似ています。したがって、潮汐ラブ数 k2 は、地下海の存在を示す良い指標となり得る。たとえば、分化を仮定し、氷殻の厚さに応じて、k2 の測定精度が 0.003 ~ 0.017 であれば、アリエルに全球的な海があることを検出できる。このような精度は、10 回のフライバイから推定されたタイタンの k2 が 0.06 の精度であることと比較すると、達成が困難であるように思われる (Goossens et al. 2024)。ただし、UOP 宇宙船によるアリエルのフライバイのジオメトリに応じて、0.010 ~ 0.015 の精度が達成される可能性がある (Filice et al., 2024)。暫定的な UOP 10 年ツアーには、高度 25 km (半径の 4%) でのアリエルへの 12 回の近接フライバイが含まれている (Simon et al.)。 (2021) 一方、カッシーニによるタイタンのフライバイは高度 1500 km 超で行われました (半径の 60%)。
天王星の衛星が 2 層の固体であれば、その秤動振幅は
オベロンで約 1 m、ミランダで約 50 m の範囲になります (セクション 3.2.1 を参照)。均質な固体と分化した固体を区別するには、オベロンで約 0.25 m、ミランダで約 6 m の測定精度が必要になります (セクション 3.2.2 を参照)。内部に全球海洋が存在する場合、分化した固体の場合よりも大きな秤動振幅が見つかりました。
ただし、固体の場合と海洋の場合の範囲は重なり合っているため、MOI に独立した制約がないと、秤動測定を使用して海洋を検出することは困難です。もしその MOI が、重力場または形状の正確な測定から数パーセントまでわかっていて、その殻の厚さが 150 km だとしたら、アリエルの海を検出するには、約 5 m の秤動推定精度が必要になります。殻の厚さを制限するには、さらに正確な測定が必要になります。参考までに、カッシーニの画像システムで測定されたミマスとエンケラドゥスの秤動精度は、1 分角 (または表面で 60 m、Tajeddine ら 2014 年、Thomas ら 2016 年) のオーダーです。狭角カメラと広角カメラの最先端の解像度が 2 インチであると仮定すると、Filice らは、 (2024) は、UOP フライバイの形状とフライバイごとにカメラで観測されるランドマークの数に応じて、アリエルの秤動振幅の精度が 0.5 ~ 15 m の範囲にあることを発見しました。潮汐変形は、固体層が硬い場合と比較して秤動振幅を減少させる効果がありますが、その効果は小型および中型の氷衛星では限られています (ミランダの場合は 2% 未満、約 10% 未満)。Nimmo (2023)、Hemingway および Nimmo (2024) で報告された最大値と比較すると、私たちの秤動値は比較的小さいです。これらの低い振幅は主に、Castillo-Rogez ら (2023) が海が存在する場合、その厚さは 50 km 以下であると考えているため、ここでは薄い殻を持つ内部モデルを考慮していないという事実によって説明されます。ranging from 0.2 to 5 m on the obliquity of Ariel, それでも、Nimmo (2023)、Hemingway と Nimmo (2024) が行ったように、より薄いシェルを考慮すると、図 1 (変形可能な固体層) と S6 (剛性固体層) で示されているように、厚いシェルよりも振動の値が大きいことがわかります。しかし、弾性変形を考慮すると振動振幅がわずかに小さくなるという彼らの主張には同意しません。周期的変形がある場合とない場合の海洋ケースを比較すると、振動振幅は完全に固体の場合の値をはるかに上回っていますが、厚さ 10 km の薄いシェルの場合、Ariel と Umbriel、または Titania と Oberon ではそれぞれ約 45% または 65% 減少しています (図 18 を参照)。図が厚いシェルよりも振動振幅が大きいため、振動振幅はより大きくなります。 Hemingway と Nimmo (2024) の S1 と S6 では、数桁にわたる対数スケールが使用されているため、この縮小を視覚化することはより困難です。変形の影響は、ミランダ (5%) のみに限定されています。これらの結果は、マグマの海を持つイオと地下の液体の海を持つエウロパの秤動振幅がそれぞれ 50% と 90% 減少したことと一致しています (Van Hoolst 他、2020、2013)。相互の重力相互作用により、天王星の衛星の軌道と赤道面は、一定の速度で歳差運動せず、傾斜と傾斜角も一定ではありません。ミランダだけが、他の衛星から隔離された物体のように歳差運動し、傾斜角と傾斜角はほぼ一定です。まず、URA111エフェメリスに永年摂動法を適用し、傾斜角振幅で特徴付けられる衛星軌道歳差運動系列を取得しました。付録Aセクションを参照してください。次に、カッシーニ状態モデルを使用して対応する傾斜角振幅を計算しました。強制および自由歳差運動周波数の値に応じて、傾斜角振幅は傾斜角振幅と同じまたは反対の符号になります。共鳴増幅は、自由周波数と強制周波数が互いに近い場合に発生します。均質固体衛星の傾斜角は、2層固体の傾斜角よりも小さくなります。たとえば、固体ミランダの均質ケースを除外するには、表面で約8mの測定精度が必要になります。セクション3.3.1を参照してください。Filice et al. (2024) は、UOP フライバイの形状とフライバイごとにカメラで観測されるランドマークの数に応じて、アリエルの傾斜角の精度が 0.2 ~ 5 m の範囲にあることを発見しましたが、1.3 m の精度が必要になります。内部に全球海洋が存在する場合、カッシーニ状態モデルは 3 つの自由モード (FP、FON、FIN) によって特徴付けられ、5 つの衛星で共鳴増幅が発生します (ミランダの場合は非常に薄い海洋がある内部のみ)。セクション 3.3.2 を参照してください。非共鳴状態では、シェル傾斜角の値はすべて、固体に予想される範囲内にほぼ収まるため、傾斜角測定から海洋を検出することは困難と思われます。衛星が共鳴状態にあることが判明した場合、海洋の存在は依然として確認できます。潮汐変形は固体層が硬い場合と比較して傾斜角を増大させる効果がありますが、天王星の小型および中型の氷衛星ではその効果は限定的です (ミランダでは 0.5% 未満、チタニアとオベロンでは最大 10%)。ここで提示した結果は、文献で時折報告される推論と矛盾しています。その推論では、氷衛星の氷殻は固体内部から機械的に分離されており、固体の場合よりも大きな傾斜角である程度独立して歳差運動すると想定されています (例: Bills および Nimmo (2008)、Chen 他 (2014)、Nimmo (2023))。この推論は、非共鳴状態であっても、回転の短い時間スケールで氷殻が固体内部からある程度独立して歳差運動するという日周秤動との類似性に基づいています。しかし、内部に液体層があり、共鳴領域外にある場合、スピン軌道共鳴状態にある物体の表面層の傾斜は固体の傾斜に近くなります。これは、歳差運動の長い時間スケールでは、物体がほぼ固体のように振舞うためです (水星については Baland (2022) とその中の参考文献、エウロパについては Coyette ら (2022) も参照)。
我々の結果は、海洋の検出や内部の制限に必要な測定精度に関する解釈に大きな影響を与えないと考えられる特定の仮定に基づいています。
たとえば、天王星の最大の衛星は、静水圧平衡からわずかに逸脱している可能性があります。ここで使用する軌道歳差の永年モデルは、軌道歳差の記述に誤差をもたらし、それが自転歳差の記述に伝播します。UOP ミッションで衛星の回転が測定される場合、静水圧平衡から逸脱する内部モデル (エンケラドゥスで行われたように、たとえば Van Hoolst ら (2016)) と、これらの測定値を解釈するためのより正確な軌道モデルを考慮する必要があるかもしれません。
この研究では、天王星の 5 つの最大の衛星の内部を制限するために、秤動、傾斜角、およびそれほどではないが潮汐測定の可能性を個別に説明しました。静重力場の推定値と潮汐力および回転力の測定を組み合わせることで、内部構造(さまざまな層のサイズ、密度、剛性)を特徴付けることができるはずです。これについては、マルコフ連鎖モンテカルロ(MCMC)アプローチを使用して天王星の衛星の内部特性を推測する関連論文でさらに詳しく説明しています。この後続の研究では、ターゲット測定の精度が計算され、UOPミッションの改良と定義に役立つ貴重な入力が提供されます(Filice et al.(2024)を参照)。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます