宇宙で重力波を捉えるのは編隊飛行するESAのLISAだけかと思ったら月面に専用の月震計を設置するアイデアも有るんだ。月震と周波数帯域が違う重力波なら風が吹かない月面は最適な場所かもしれない。以下、機械翻訳。
重力波に対する月の応答の一貫した計算に向けて
最近、月の地震測定による重力波 (GW) の検出への関心が高まっているため、重力波の通過に対する月の反応を明確に理解することが求められています。 この中で
この論文では、一見異なる 2 つの応答関数間の関係を明らかにしています。
1 つは場の理論アプローチを採用し、もう 1 つは 2 つの異なる方法を使用して以前に導出されました。
GWによって引き起こされる潮汐力を利用します。 それらの導出を再検討し、両方の分析によって証明します。
引数と数値計算により、2 つの応答関数が同等であることがわかります。 それらの明らかな違いは、異なる座標の選択に起因すると考えられます。 正しい応答を使用する
関数を使用して、いくつかの設計された月地震計の(GW に対する)感度を計算し、
感度が 10^−3と 0.1 Hz の間で変化することは前の計算よりもはるかに平坦です
ノーマルモードモデルをベースにしています。 私たちの結果は、月のGWの科学的目的を明らかにするのに役立ちます
月の GW 検出器の設計に重要な制約を与えるだけでなく、観測にも影響を及ぼします。
I.はじめに
10~10^2 Hz [1] およびナノ Hz [2〜5] の周波数窓における重力波 (GW) の検出
他の周波数で GW を検出する取り組みを奨励します
バンド。 いくつかのプロジェクトでは、干渉計を使用して次のことを行うことを計画しています。
レーザー干渉計宇宙アンテナ (LISA [6])、TianQin [7]、および
太地[8]。 また、デシヘルツ (0.1 Hz またはデシヘルツ) GW をプローブする干渉計の議論と設計も行われています。
[9]、DECIGO [10] や TVLBAI [11] など。
別のアプローチは、
月の静けさを検出し、それを共鳴GW検出器として使用します[12]。 しかし、月の反応を検知すると、
GWを通過するには月の地震計の再設計が必要になる
特に高い感度を実現します。 最近の
いくつかの設計に基づく研究では、GW に対する感度がデシヘルツ付近で最も優れていることが示唆されています。
白色矮星連星、中間質量ブラックホール連星(IMBHB)、および超大質量星の合体を検出します。
宇宙論的距離にあるブラックホール連星 (SMBHB) と、その中で生成される GW バックグラウンド
初期宇宙[13、14]。
月の反応を研究する上で不可欠な要素の 1 つ
から GW は、次によって課される力密度の計算です。
弾力のあるボディにGW。 この理論を最初に確立したのは、
ダイソン([15]、以下Dy69)。 彼は畑からスタートした
理論と、GW 間の結合項を導入することにより、
と弾性体から外力密度を導き出す
⃗f = −∇ · (μh) 、
ここで、μ はせん断弾性率、h は 3-
GW テンソルの次元空間成分。 ダイソンは、この方程式を使用して、通過する GW の列車に対する有限の半空間の応答を研究しました。 その後、ベン・メナヘムは同じ力密度を、より現実的な月のモデルである放射状に不均一な弾性球に適用しました。
そして分析応答解を導き出しました ([16]、BM83 以降)。 派生の最新バージョンでは、
参考文献に記載されています。 [17](以下、Ma19)。 Dy69 と Ma19 で導出されたこれらの式は、多くの基礎を形成します。
GWに対する月または地球の反応のその後の計算
[18-21]。 彼らは科学にも大きな影響を与えました
最近の月面GWプロジェクトの目的
月の GW アンテナ (LGWA、[13、22])。
しかし、月の応答関数を計算するために別の視点を取ると、あいまいさが現れます。
地上設置型バー探知機の初期の研究では [23-27]ではGWによる力密度を書くのが一般的
の形で
⃗f = 1/2・ρ・d^2h/dt^2· ⃗r 、
ここで、ρ は質量密度、⃗r は位置ベクトルです。
この式は通常「ムラの潮汐加速度」と呼ばれ、多くの教科書で採用されています(例:[28、29])。 最近の科学研究でも使われています。
月地震計プロジェクト [14]。 明らかな違い
この方程式を前の方程式と比較すると、当然、どの力密度を適用すべきかという疑問が生じます。
月の応答の計算に使用されます。
この曖昧さは、以前のいくつかの論文で指摘されています。 完全な一般相対論を開発しようとする彼の試みの中で、
月の反応[30]の扱いにドズモロフは気づいた
2 つの力密度の差 [31]。 彼
その違いは2種類のせん断波によるものだと考えられ、
1 つは光の速度で伝播し、もう 1 つは光の速度で伝播します。
地震波の速度。 しかし、その原因や関係についてはこれ以上の説明はしなかった。
この二つの波。 最近のレビュー記事 [32] (以下、
Ha19) は、ダイソンの物理的意味についても説明しています。
ニュートン力学で計算された表面変位と、
慣性センサーによって測定された変位。 それは主張します
2 つの変位が等しいことを示唆しています。
2 つの変位は次の変化によって接続されます。
座標系ですが、定量的な証拠はまだありません
欠けている。 おそらく決定的でないため、
以前の議論、後の作品が時々考慮される
両方のタイプの力と 2 つの応答関数を示しました。
これらのこれまでの議論に触発されて、私たちは次のことを決定しました。
関連する理論を再検討し、前述の 2 つによって引き起こされる親の不一致を解決しようとします。
力密度の種類。 論文は以下のように構成されています。 セクション II では、力学方程式を確認します。
ダイソン力を受ける弾性体の
または潮汐力。ここでは、座標系間の物理的な違いを明らかにすることに焦点を当てています。
方程式が導き出されます。 次に 2 つの応答を導き出します
上記 2 種類の力に対応する関数、
そして、それらを 1 つの分析に統合できることを示します。
式。 セクション III では、応答関数を均一等方性球と実際の月に適用します。
モデルを使用して、両方のケースで数値結果が得られることを示します。
分析関係に同意します。 議論もします
適切な応答関数に基づく GW の可観測性。 最後に、セクション IV で次のようにまとめます。
私たちの結果を紹介し、将来の月への影響について議論します
GW観察。 この文書全体を通して、私たちは採用します
国際単位系とミンコフスキー
特に指定のない限り、計量 ημν = diag (−1, 1, 1, 1)。 ラテン文字は 3 つの空間インデックスを表します。
ギリシャ文字は時空インデックスを表します。

図。 1. 均一系の動径応答関数 Tr(f)
異なる層数を使用して計算された等方性球
NL。 両方の軸が log10 スケールであることに注意してください。 結果
ダイソン力 (TAr ) と潮汐力 (TBr −0.5R) は、比較しやすいように同じプロットに表示されます。

図。 2. この論文で使用されている現実的な月のモデル。 の
1 つの単位を使用して 3 つの曲線をプロットできるように単位が選択されます。
x 軸。

図。 3. 現実的な月モデルの応答関数。 (a)
ダイソン力(A) と潮汐力 (B)から導出されたラジアル応答関数 Tr(f)。
(b) 水平応答関数2 つの力の Th(f)。 (c) 古い応答関数 TBとTBh は、[13] で与えられた方法に従って導出されます。
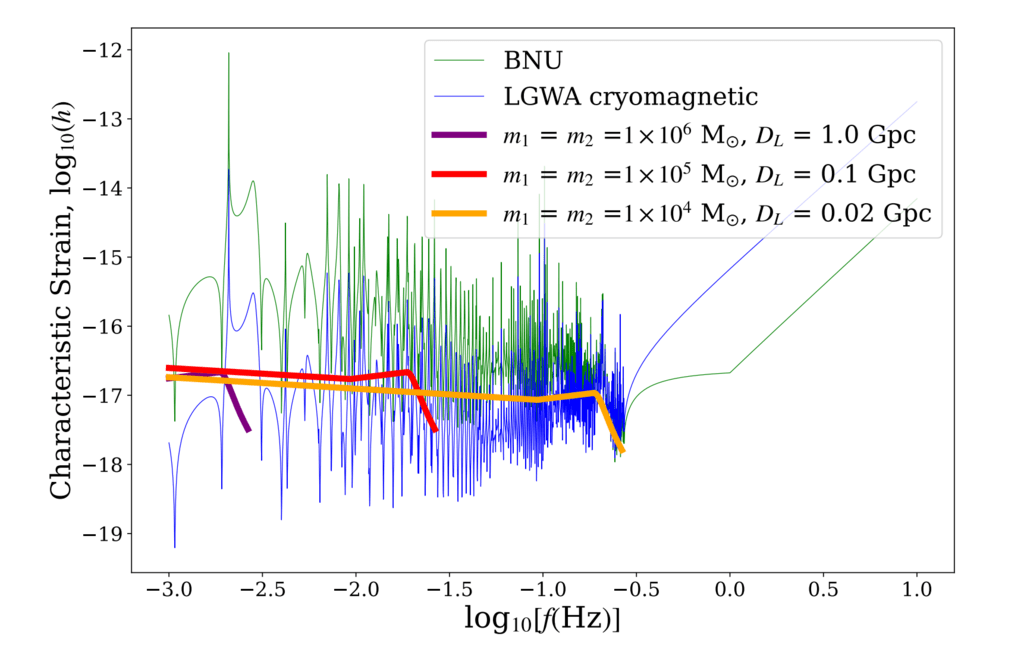
図。 4. さまざまな機器の GW 特性ひずみ
(細線) および代表的な天体物理学バイナリ
ソース(太線)。
IV. まとめと結論
この論文では、GW に対する月の応答を計算する理論を再検討しました。 2 つの応答に関する文献に存在する曖昧さを明確にしました。
2 つの観点から導き出された関数。
ダイソン力 (式 6')
)、もう一方は通常の潮汐力からのものです (式 10)。 2 つの関数間の親の違いが原因であることを示しました。
さまざまなコーディネートを選択してください。
この理解に基づいて、私たちは簡潔で
2 つの関数間の明確な関係 (式 26 を参照)。 私たちは、次の方法を使用して計算された数値応答関数を比較することで、この分析関係を検証しました。
それぞれ、ダイソン力と潮汐力です (図 3 を参照)。
より低い周波数では良好な一致が見られました。 の
より高い周波数での偏差は (i) に起因する可能性があります。
一定の高値を超える通常モードの切り捨て
計算における n の値、および (ii) の制限
月モデルに実装したレイヤーの数。
新しい応答関数は、
将来の月地震計によるGW震源の検出可能性。 図 4 が示すように、検出器の現在の設計を考慮すると、GW に対する感度は次の期間で平坦になります。
10^−3 および 0.1 Hz、デシヘルツ GW の検出を行う
これまで考えられていたよりも挑戦的です。 特に、デシヘルツ GW 帯域の重要な発生源である IMBHB と SMBHB を検出するには、次のことが不可欠です。
10^−3 ~ 0.1 Hz の周波数帯域で極低温磁気検出器設計よりも優れた感度を達成
LGWAプロジェクトによる。 私たちの結果が役に立つと信じています
月のGW観測の科学的目標を形作るだけでなく、月のGW観測に重要な制約を与える。
月のGW検出器の設計。
最後に、私たちの対応について指摘しておきたいと思います。
関数は現在のノーマルモードに基づいて導出されます
GW場における弾性系の力学方程式の定式化。 重要な側面があります。
からのデータによると、現在のノーマルモードモデルでは捉えられない月の地震応答。
アポロの地震観測 [13, 40]。 さらなる研究
月の構造と月の地震応答は慎重に必要とされています。
重力波に対する月の応答の一貫した計算に向けて
最近、月の地震測定による重力波 (GW) の検出への関心が高まっているため、重力波の通過に対する月の反応を明確に理解することが求められています。 この中で
この論文では、一見異なる 2 つの応答関数間の関係を明らかにしています。
1 つは場の理論アプローチを採用し、もう 1 つは 2 つの異なる方法を使用して以前に導出されました。
GWによって引き起こされる潮汐力を利用します。 それらの導出を再検討し、両方の分析によって証明します。
引数と数値計算により、2 つの応答関数が同等であることがわかります。 それらの明らかな違いは、異なる座標の選択に起因すると考えられます。 正しい応答を使用する
関数を使用して、いくつかの設計された月地震計の(GW に対する)感度を計算し、
感度が 10^−3と 0.1 Hz の間で変化することは前の計算よりもはるかに平坦です
ノーマルモードモデルをベースにしています。 私たちの結果は、月のGWの科学的目的を明らかにするのに役立ちます
月の GW 検出器の設計に重要な制約を与えるだけでなく、観測にも影響を及ぼします。
I.はじめに
10~10^2 Hz [1] およびナノ Hz [2〜5] の周波数窓における重力波 (GW) の検出
他の周波数で GW を検出する取り組みを奨励します
バンド。 いくつかのプロジェクトでは、干渉計を使用して次のことを行うことを計画しています。
レーザー干渉計宇宙アンテナ (LISA [6])、TianQin [7]、および
太地[8]。 また、デシヘルツ (0.1 Hz またはデシヘルツ) GW をプローブする干渉計の議論と設計も行われています。
[9]、DECIGO [10] や TVLBAI [11] など。
別のアプローチは、
月の静けさを検出し、それを共鳴GW検出器として使用します[12]。 しかし、月の反応を検知すると、
GWを通過するには月の地震計の再設計が必要になる
特に高い感度を実現します。 最近の
いくつかの設計に基づく研究では、GW に対する感度がデシヘルツ付近で最も優れていることが示唆されています。
白色矮星連星、中間質量ブラックホール連星(IMBHB)、および超大質量星の合体を検出します。
宇宙論的距離にあるブラックホール連星 (SMBHB) と、その中で生成される GW バックグラウンド
初期宇宙[13、14]。
月の反応を研究する上で不可欠な要素の 1 つ
から GW は、次によって課される力密度の計算です。
弾力のあるボディにGW。 この理論を最初に確立したのは、
ダイソン([15]、以下Dy69)。 彼は畑からスタートした
理論と、GW 間の結合項を導入することにより、
と弾性体から外力密度を導き出す
⃗f = −∇ · (μh) 、
ここで、μ はせん断弾性率、h は 3-
GW テンソルの次元空間成分。 ダイソンは、この方程式を使用して、通過する GW の列車に対する有限の半空間の応答を研究しました。 その後、ベン・メナヘムは同じ力密度を、より現実的な月のモデルである放射状に不均一な弾性球に適用しました。
そして分析応答解を導き出しました ([16]、BM83 以降)。 派生の最新バージョンでは、
参考文献に記載されています。 [17](以下、Ma19)。 Dy69 と Ma19 で導出されたこれらの式は、多くの基礎を形成します。
GWに対する月または地球の反応のその後の計算
[18-21]。 彼らは科学にも大きな影響を与えました
最近の月面GWプロジェクトの目的
月の GW アンテナ (LGWA、[13、22])。
しかし、月の応答関数を計算するために別の視点を取ると、あいまいさが現れます。
地上設置型バー探知機の初期の研究では [23-27]ではGWによる力密度を書くのが一般的
の形で
⃗f = 1/2・ρ・d^2h/dt^2· ⃗r 、
ここで、ρ は質量密度、⃗r は位置ベクトルです。
この式は通常「ムラの潮汐加速度」と呼ばれ、多くの教科書で採用されています(例:[28、29])。 最近の科学研究でも使われています。
月地震計プロジェクト [14]。 明らかな違い
この方程式を前の方程式と比較すると、当然、どの力密度を適用すべきかという疑問が生じます。
月の応答の計算に使用されます。
この曖昧さは、以前のいくつかの論文で指摘されています。 完全な一般相対論を開発しようとする彼の試みの中で、
月の反応[30]の扱いにドズモロフは気づいた
2 つの力密度の差 [31]。 彼
その違いは2種類のせん断波によるものだと考えられ、
1 つは光の速度で伝播し、もう 1 つは光の速度で伝播します。
地震波の速度。 しかし、その原因や関係についてはこれ以上の説明はしなかった。
この二つの波。 最近のレビュー記事 [32] (以下、
Ha19) は、ダイソンの物理的意味についても説明しています。
ニュートン力学で計算された表面変位と、
慣性センサーによって測定された変位。 それは主張します
2 つの変位が等しいことを示唆しています。
2 つの変位は次の変化によって接続されます。
座標系ですが、定量的な証拠はまだありません
欠けている。 おそらく決定的でないため、
以前の議論、後の作品が時々考慮される
両方のタイプの力と 2 つの応答関数を示しました。
これらのこれまでの議論に触発されて、私たちは次のことを決定しました。
関連する理論を再検討し、前述の 2 つによって引き起こされる親の不一致を解決しようとします。
力密度の種類。 論文は以下のように構成されています。 セクション II では、力学方程式を確認します。
ダイソン力を受ける弾性体の
または潮汐力。ここでは、座標系間の物理的な違いを明らかにすることに焦点を当てています。
方程式が導き出されます。 次に 2 つの応答を導き出します
上記 2 種類の力に対応する関数、
そして、それらを 1 つの分析に統合できることを示します。
式。 セクション III では、応答関数を均一等方性球と実際の月に適用します。
モデルを使用して、両方のケースで数値結果が得られることを示します。
分析関係に同意します。 議論もします
適切な応答関数に基づく GW の可観測性。 最後に、セクション IV で次のようにまとめます。
私たちの結果を紹介し、将来の月への影響について議論します
GW観察。 この文書全体を通して、私たちは採用します
国際単位系とミンコフスキー
特に指定のない限り、計量 ημν = diag (−1, 1, 1, 1)。 ラテン文字は 3 つの空間インデックスを表します。
ギリシャ文字は時空インデックスを表します。

図。 1. 均一系の動径応答関数 Tr(f)
異なる層数を使用して計算された等方性球
NL。 両方の軸が log10 スケールであることに注意してください。 結果
ダイソン力 (TAr ) と潮汐力 (TBr −0.5R) は、比較しやすいように同じプロットに表示されます。

図。 2. この論文で使用されている現実的な月のモデル。 の
1 つの単位を使用して 3 つの曲線をプロットできるように単位が選択されます。
x 軸。

図。 3. 現実的な月モデルの応答関数。 (a)
ダイソン力(A) と潮汐力 (B)から導出されたラジアル応答関数 Tr(f)。
(b) 水平応答関数2 つの力の Th(f)。 (c) 古い応答関数 TBとTBh は、[13] で与えられた方法に従って導出されます。

図。 4. さまざまな機器の GW 特性ひずみ
(細線) および代表的な天体物理学バイナリ
ソース(太線)。
IV. まとめと結論
この論文では、GW に対する月の応答を計算する理論を再検討しました。 2 つの応答に関する文献に存在する曖昧さを明確にしました。
2 つの観点から導き出された関数。
ダイソン力 (式 6')
)、もう一方は通常の潮汐力からのものです (式 10)。 2 つの関数間の親の違いが原因であることを示しました。
さまざまなコーディネートを選択してください。
この理解に基づいて、私たちは簡潔で
2 つの関数間の明確な関係 (式 26 を参照)。 私たちは、次の方法を使用して計算された数値応答関数を比較することで、この分析関係を検証しました。
それぞれ、ダイソン力と潮汐力です (図 3 を参照)。
より低い周波数では良好な一致が見られました。 の
より高い周波数での偏差は (i) に起因する可能性があります。
一定の高値を超える通常モードの切り捨て
計算における n の値、および (ii) の制限
月モデルに実装したレイヤーの数。
新しい応答関数は、
将来の月地震計によるGW震源の検出可能性。 図 4 が示すように、検出器の現在の設計を考慮すると、GW に対する感度は次の期間で平坦になります。
10^−3 および 0.1 Hz、デシヘルツ GW の検出を行う
これまで考えられていたよりも挑戦的です。 特に、デシヘルツ GW 帯域の重要な発生源である IMBHB と SMBHB を検出するには、次のことが不可欠です。
10^−3 ~ 0.1 Hz の周波数帯域で極低温磁気検出器設計よりも優れた感度を達成
LGWAプロジェクトによる。 私たちの結果が役に立つと信じています
月のGW観測の科学的目標を形作るだけでなく、月のGW観測に重要な制約を与える。
月のGW検出器の設計。
最後に、私たちの対応について指摘しておきたいと思います。
関数は現在のノーマルモードに基づいて導出されます
GW場における弾性系の力学方程式の定式化。 重要な側面があります。
からのデータによると、現在のノーマルモードモデルでは捉えられない月の地震応答。
アポロの地震観測 [13, 40]。 さらなる研究
月の構造と月の地震応答は慎重に必要とされています。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます