
小惑星クレオパトラは自転軸が安定していないタンブリング状態。以下、機械翻訳。
(216)クレオパトラトリプルシステムの高度な多重極モデル
(216)クレオパトラの補償光学観測を解釈するには、非常に不規則な物体を周回し、それらの相互作用を含む、複数の衛星の進化を説明する必要があります。このような軌道は一般に非ケプラーであり、軌道要素は定数ではありません。その結果、修正された$ N $ -body積分器を使用します。これは、$ \ ell = 10 $のオーダーまでの重力場の多重極展開を含むように大幅に拡張されました。その収束は、「ブルートフォース」アルゴリズムに対して検証されました。かさ密度が一定であると仮定して、クレオパトラの形状の係数$ C _ {\ ell m}、S _ {\!\ ell m} $を計算しました。太陽系のアプリケーションでは、観測の可変距離とジオメトリを実装することも必要でした。次に、$ \ chi ^ 2 $メトリックは、絶対位置天文学を説明します。相対位置天文学(1番目に対する2番目の月)、角速度、およびシルエットも、極の向きを制約します。これにより、クレオパトラの2つの衛星の軌道要素を導き出すことができました。アーカイブの位置天文データと新しいVLT / SPHERE観測(ESO LP 199.C-0074)の両方を使用して、衛星の真の周期を特定することができました。$ P_1 =(1.822359 \ pm0.004156)\、{\ rm d} $、$ P_2 =(2.745820 \ pm0.004820)\、{\ rm d} $。それらは3:2平均運動共鳴に非常に近い軌道を回っていますが、それらの接触離心率は他の摂動(多重極、相互)と比較して小さすぎるため、重要な議論の定期的な秤動は存在しません。結果として得られるクレオパトラの質量、$ m_1 =(1.49 \ pm0.16)\ cdot10 ^ {-12} \、M_ \ odot $または$ 2.97 \ cdot10 ^ {18} \、{\ rm kg} $は、以前に考えた。 N体積分器。これは、オーダーまでの重力場の多重極展開を含むように大幅に拡張されました。その収束は、「ブルートフォース」アルゴリズムに対して検証されました。かさ密度が一定であると仮定して、クレオパトラの形状の係数を計算しました。太陽系のアプリケーションでは、観測の可変距離とジオメトリを実装することも必要でした。私たちのℓ = 10Cℓのメートル、Sℓのメートルχ2 次に、メートル法は、絶対位置天文学、相対位置天文学(1番目に対する2番目の月)、角速度、およびシルエットを考慮して、極の向きを制約します。これにより、クレオパトラの2つの衛星の軌道要素を導き出すことができました。アーカイブの位置天文データと新しいVLT / SPHERE観測(ESO LP 199.C-0074)の両方を使用して、衛星の真の周期を特定することができました、。それらは3:2平均運動共鳴に非常に近い軌道を回っていますが、それらの接触離心率は他の摂動(多重極、相互)と比較して小さすぎるため、重要な議論の定期的な秤動は存在しません。結果として得られるクレオパトラの質量、P1= (1.822359 ± 0.004156 )dP2= (2.745820 ± 0.004820 )dm1= (1.49 ± 0.16 )⋅10− 12M⊙またはは、以前に考えられていたよりも大幅に低くなっています。添付の論文(Marchis et al。)で説明されている含意は、(216)クレオパトラが臨界回転体であるということです。 2.97×10^18k g
キーワード。 小惑星、小惑星 (216)クレオパトラ 惑星と衛星 基本的なパラメーター 位置天文学 天体力学 方法 数値
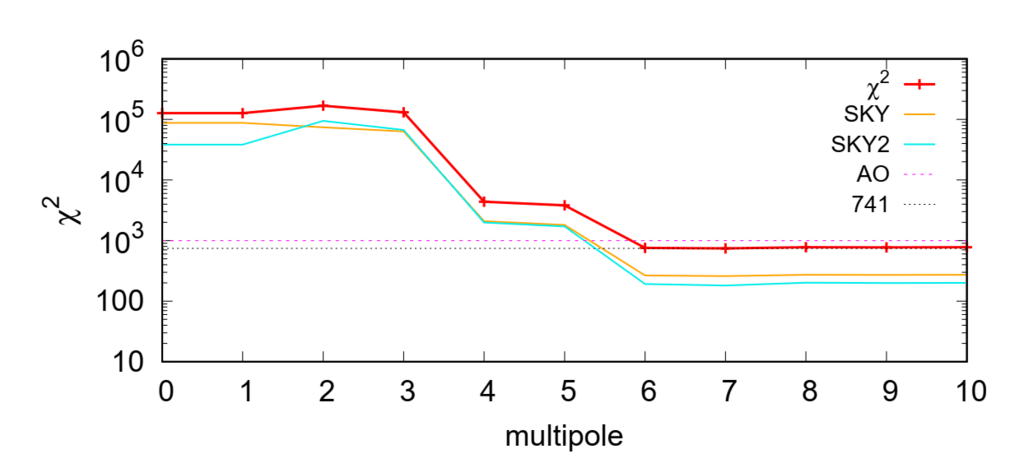
図1.χ^2の依存性 =χ^2sky+χ^2sky2 +0.3χ^2ao
多重極次数のℓ。 モデルはℓ= 10に最適化され、その後
低次の再計算(最適化されていない)。 のは大事です
注文ℓ≤6を説明します。
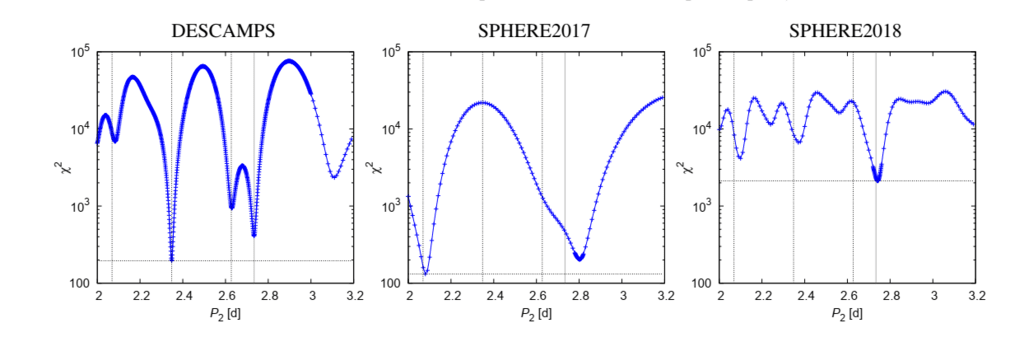
図2.3つのデータセット(DESCAMPS、SPHERE2017、SPHERE2018)に対して別々に計算されたP2のピリオドグラム。 χ2 =χ2sky
値は最初のデータセット用に最適化され、次にP2のみが変更されました。 古い誤った期間(点線)を一緒に表示します
タイムスパン∆P = P2 /(t2 − t1)で与えられる極小値と、新しい正しい極小値(灰色の線)との間の予想される間隔。 シフト
SPHERE2017のP2の増加とχ2の増加
SPHERE2018は、2つの衛星の識別が正しくないために存在していました。 そうだった
ピリオドグラムを計算した後、軌道をフィッティングする前に修正されました。
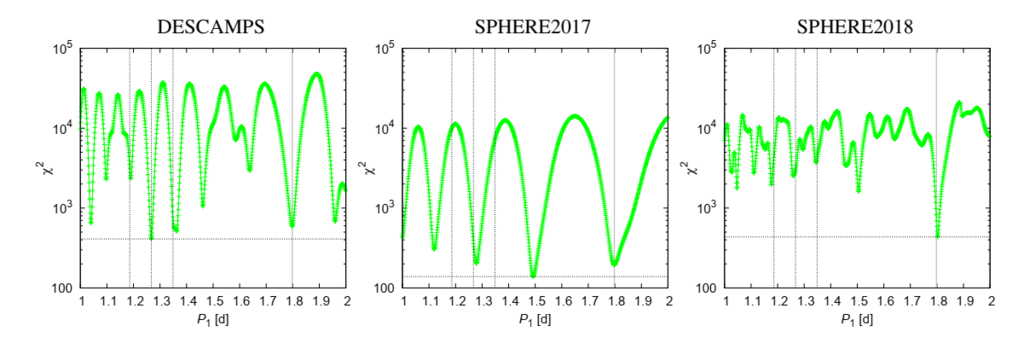
図3.P1の図2と同じですが、P2はすでに約2.7dに向かってシフトしています。
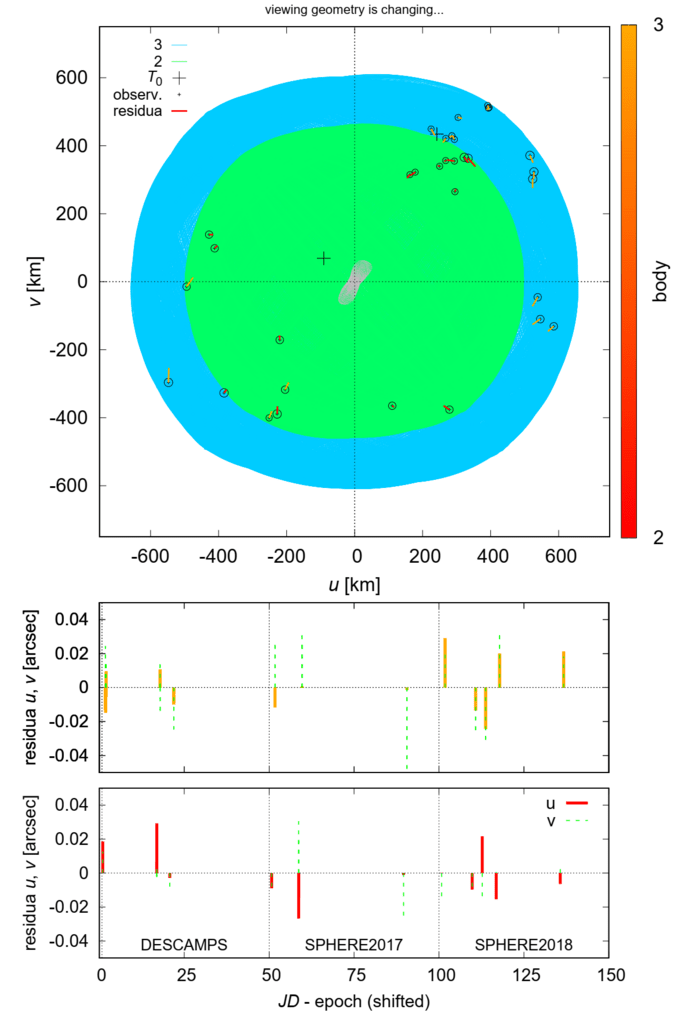
図4.χ^2を使用した最適モデル =χ^2sky+χ^2sky2 +0.3χ^2ao = 368。
上:(u、v)座標(青、緑の線)でプロットされたクレオパトラの衛星の軌道、観測された絶対位置天文学(SKY;黒丸)、および残差(ボディ2、3の赤、オレンジの線)
つまり、内側と外側の衛星)。 クレオパトラの形状モデルエポックの1つは灰色でオーバープロットされています。 軸はスケーリングされます
km単位; 可変の表示ジオメトリを使用しますが、可変の距離はありません。 軌道の平均準主軸は次のとおりです。a1
499 km、a2 655 km 下:秒単位の(u、v)の残差
3つのデータセット(DESCAMPS、SPHERE2017、
SPHERE2018)。 位置天文観測の不確実性
約0.01秒角でした。
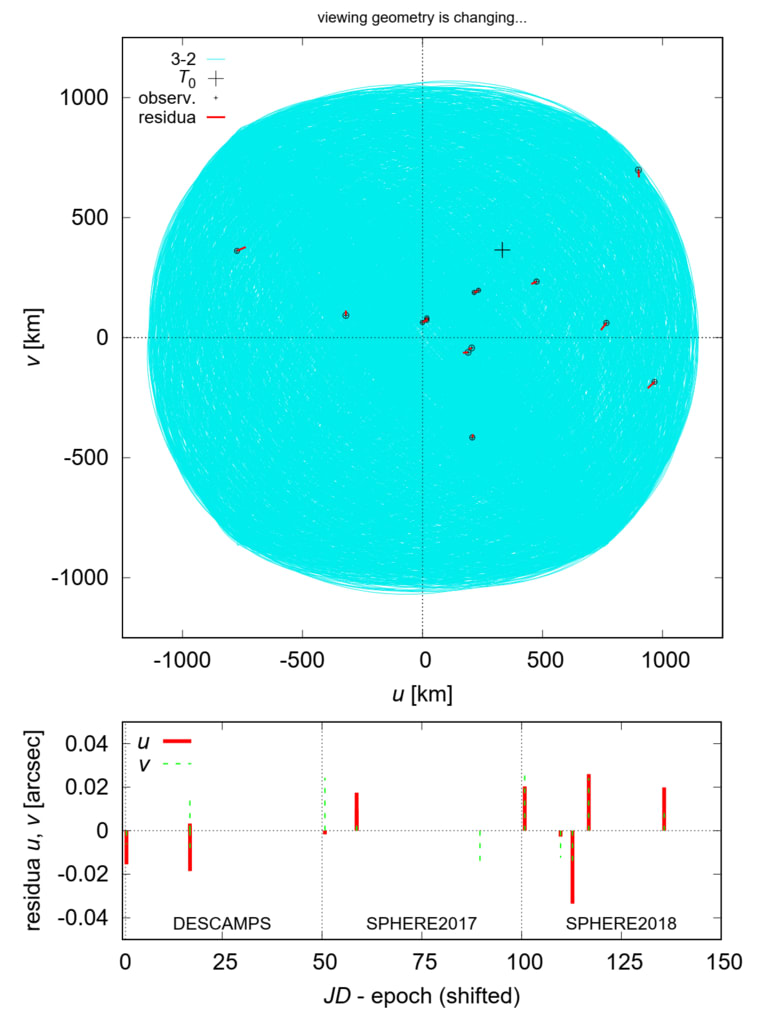
図5.図4と同じですが、相対位置天文学用です(SKY2; 3番目
ボディwrt。 2番目)。 したがって、点(0,0)は内衛星を中心とします。

図6.(u、v)座標(オレンジ)でのクレオパトラのシルエット、
9つのエポック(JD − 2400000.0)について計算され、
SPHERE2017、SPHERE2018の観測値(青)、および残差(赤)。
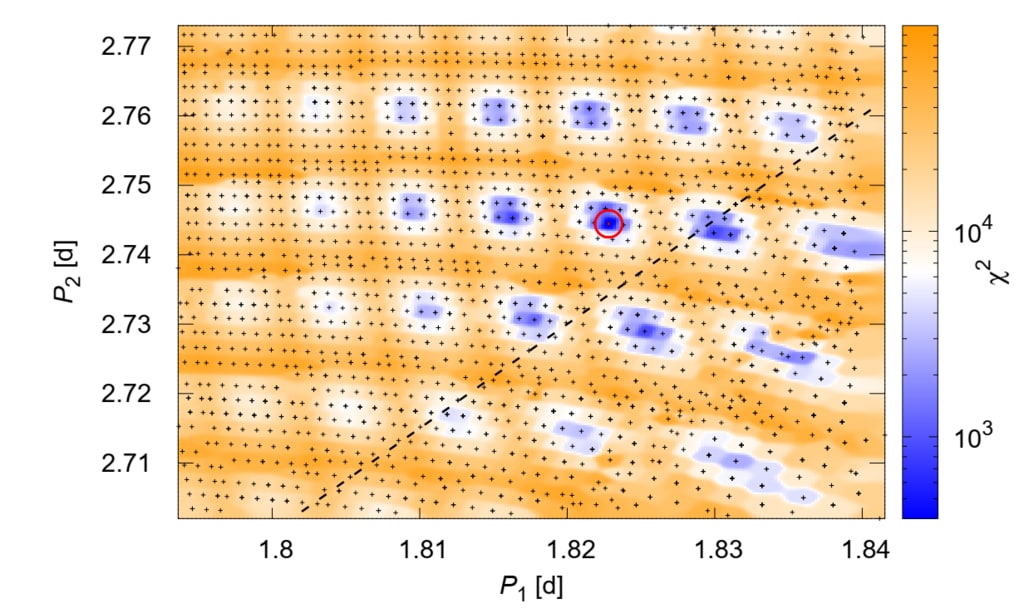
図7.χ^2 =χ^2sky
期間P1、P2および最適化されたモデルの範囲の空の値。 すべての黒い十字は極小値を示します(つまり、
単純なχ^2map)ではありません。 すべてのデータセット(DESCAMPS、SPHERE2017、
SPHERE2018)が一緒に使用されたため、間隔が
極小値の間は非常に細かいです。 グローバル最小値は赤い円で示されます。 破線は正確な3:2を示します
期間比率。

図8.χ^2 =χ^2sky+χ^2sky2月の質量の範囲の値
m2、m3。 すべてのモデルは、期間に関して最適化されました
P1、P2。 その他のパラメータが修正されました。 グローバル最小値は
赤い丸で示されています。
(216)クレオパトラトリプルシステムの高度な多重極モデル
(216)クレオパトラの補償光学観測を解釈するには、非常に不規則な物体を周回し、それらの相互作用を含む、複数の衛星の進化を説明する必要があります。このような軌道は一般に非ケプラーであり、軌道要素は定数ではありません。その結果、修正された$ N $ -body積分器を使用します。これは、$ \ ell = 10 $のオーダーまでの重力場の多重極展開を含むように大幅に拡張されました。その収束は、「ブルートフォース」アルゴリズムに対して検証されました。かさ密度が一定であると仮定して、クレオパトラの形状の係数$ C _ {\ ell m}、S _ {\!\ ell m} $を計算しました。太陽系のアプリケーションでは、観測の可変距離とジオメトリを実装することも必要でした。次に、$ \ chi ^ 2 $メトリックは、絶対位置天文学を説明します。相対位置天文学(1番目に対する2番目の月)、角速度、およびシルエットも、極の向きを制約します。これにより、クレオパトラの2つの衛星の軌道要素を導き出すことができました。アーカイブの位置天文データと新しいVLT / SPHERE観測(ESO LP 199.C-0074)の両方を使用して、衛星の真の周期を特定することができました。$ P_1 =(1.822359 \ pm0.004156)\、{\ rm d} $、$ P_2 =(2.745820 \ pm0.004820)\、{\ rm d} $。それらは3:2平均運動共鳴に非常に近い軌道を回っていますが、それらの接触離心率は他の摂動(多重極、相互)と比較して小さすぎるため、重要な議論の定期的な秤動は存在しません。結果として得られるクレオパトラの質量、$ m_1 =(1.49 \ pm0.16)\ cdot10 ^ {-12} \、M_ \ odot $または$ 2.97 \ cdot10 ^ {18} \、{\ rm kg} $は、以前に考えた。 N体積分器。これは、オーダーまでの重力場の多重極展開を含むように大幅に拡張されました。その収束は、「ブルートフォース」アルゴリズムに対して検証されました。かさ密度が一定であると仮定して、クレオパトラの形状の係数を計算しました。太陽系のアプリケーションでは、観測の可変距離とジオメトリを実装することも必要でした。私たちのℓ = 10Cℓのメートル、Sℓのメートルχ2 次に、メートル法は、絶対位置天文学、相対位置天文学(1番目に対する2番目の月)、角速度、およびシルエットを考慮して、極の向きを制約します。これにより、クレオパトラの2つの衛星の軌道要素を導き出すことができました。アーカイブの位置天文データと新しいVLT / SPHERE観測(ESO LP 199.C-0074)の両方を使用して、衛星の真の周期を特定することができました、。それらは3:2平均運動共鳴に非常に近い軌道を回っていますが、それらの接触離心率は他の摂動(多重極、相互)と比較して小さすぎるため、重要な議論の定期的な秤動は存在しません。結果として得られるクレオパトラの質量、P1= (1.822359 ± 0.004156 )dP2= (2.745820 ± 0.004820 )dm1= (1.49 ± 0.16 )⋅10− 12M⊙またはは、以前に考えられていたよりも大幅に低くなっています。添付の論文(Marchis et al。)で説明されている含意は、(216)クレオパトラが臨界回転体であるということです。 2.97×10^18k g
キーワード。 小惑星、小惑星 (216)クレオパトラ 惑星と衛星 基本的なパラメーター 位置天文学 天体力学 方法 数値

図1.χ^2の依存性 =χ^2sky+χ^2sky2 +0.3χ^2ao
多重極次数のℓ。 モデルはℓ= 10に最適化され、その後
低次の再計算(最適化されていない)。 のは大事です
注文ℓ≤6を説明します。

図2.3つのデータセット(DESCAMPS、SPHERE2017、SPHERE2018)に対して別々に計算されたP2のピリオドグラム。 χ2 =χ2sky
値は最初のデータセット用に最適化され、次にP2のみが変更されました。 古い誤った期間(点線)を一緒に表示します
タイムスパン∆P = P2 /(t2 − t1)で与えられる極小値と、新しい正しい極小値(灰色の線)との間の予想される間隔。 シフト
SPHERE2017のP2の増加とχ2の増加
SPHERE2018は、2つの衛星の識別が正しくないために存在していました。 そうだった
ピリオドグラムを計算した後、軌道をフィッティングする前に修正されました。

図3.P1の図2と同じですが、P2はすでに約2.7dに向かってシフトしています。

図4.χ^2を使用した最適モデル =χ^2sky+χ^2sky2 +0.3χ^2ao = 368。
上:(u、v)座標(青、緑の線)でプロットされたクレオパトラの衛星の軌道、観測された絶対位置天文学(SKY;黒丸)、および残差(ボディ2、3の赤、オレンジの線)
つまり、内側と外側の衛星)。 クレオパトラの形状モデルエポックの1つは灰色でオーバープロットされています。 軸はスケーリングされます
km単位; 可変の表示ジオメトリを使用しますが、可変の距離はありません。 軌道の平均準主軸は次のとおりです。a1
499 km、a2 655 km 下:秒単位の(u、v)の残差
3つのデータセット(DESCAMPS、SPHERE2017、
SPHERE2018)。 位置天文観測の不確実性
約0.01秒角でした。

図5.図4と同じですが、相対位置天文学用です(SKY2; 3番目
ボディwrt。 2番目)。 したがって、点(0,0)は内衛星を中心とします。

図6.(u、v)座標(オレンジ)でのクレオパトラのシルエット、
9つのエポック(JD − 2400000.0)について計算され、
SPHERE2017、SPHERE2018の観測値(青)、および残差(赤)。

図7.χ^2 =χ^2sky
期間P1、P2および最適化されたモデルの範囲の空の値。 すべての黒い十字は極小値を示します(つまり、
単純なχ^2map)ではありません。 すべてのデータセット(DESCAMPS、SPHERE2017、
SPHERE2018)が一緒に使用されたため、間隔が
極小値の間は非常に細かいです。 グローバル最小値は赤い円で示されます。 破線は正確な3:2を示します
期間比率。

図8.χ^2 =χ^2sky+χ^2sky2月の質量の範囲の値
m2、m3。 すべてのモデルは、期間に関して最適化されました
P1、P2。 その他のパラメータが修正されました。 グローバル最小値は
赤い丸で示されています。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます