巨大惑星衛星の形成

先週の木星の惑星間円盤の光蒸発I.カリストの軌道と外側の通常の衛星の欠如を説明するとラップする内容です。ガス惑星の周辺円盤には原始惑星系円盤から材料供給があるので複数回の衛星形成が可能説です。以下、機械翻訳。
巨大惑星衛星の形成
2020年5月17日に提出
最近の分析では、巨大惑星の形成の最終段階には、惑星のヒル圏内のガスの大規模な子午線流の発達が伴うことが示されています。この循環は、システムを準定常状態に維持して、気体物質を親星雲に粘性的に排出する惑星の円盤に供給します。ここでは、この新たに概説された画像の枠組みの中で、木星と土星の自然衛星の形成を調査します。固体物質の長期的な進化を検討することから始め、惑星の円盤が地球規模のダストトラップとして機能できることを示します。s∙〜0.1〜- 10mm粒子は、流体力学的平衡を達成し、放射状上昇気流と空気力学的抗力の間のバランスによって促進されます。このプロセスは、システムの金属性を徐々に増加させ、最終的には固体サブディスクの外側領域の重力による断片化に至ります。R〜100km衛星。その後、衛星の集塊はペアワイズ衝突を介して発生しますが、ディスク駆動の軌道の移動が衛星の餌場から成長しているオブジェクトを削除すると終了します。結果の衛星形成サイクルは、親星雲の光蒸発によって終了するまで、複数回繰り返すことができます。想定される形成シナリオの数値シミュレーションは、私たちのモデルと木星および土星の衛星の既知の特性との間に満足のいく一致をもたらします。

図1.モデルの定性的なスケッチ。質量Mの巨大惑星M◦〜10−3Mがギャップをクリアしたと想定されています
その親星雲内で、惑星の丘圏内のガスの定常状態の方位角/子午面循環をもたらします。なので
星雲物質がギャップの上部をオーバーフローします（高度は中立面から約1圧力スケールの高さ）。
それは惑星に向かって自由落下します–効果的な質量流束M˙〜0.1M◦/ Myrによってパラメーター化するプロセス。保全のため
角運動量のこの物質は、スピンアップして、惑星周囲の円盤を形成します。このディスクの内側のエッジは、
半径RT〜5 RJupでの惑星磁場B〜1,000 G内の（磁気-）流体力学的乱流のために
惑星周縁円盤–標準α〜10−4処方でパラメータ化–この円盤は粘性で広がり、
星状星雲に戻る降伏の着実なパターン。
ディスク内の粘性加熱と放射損失のバランスにより、システムのアスペクト比、h / r〜0.1が決まります。の
関連する圧力サポートは、ガスのサブケプラー回転を引き起こし、その結果、
惑星の周りの流れはvr〜10−5
vK＞ 0およびvφ〜0.99 vK ＜vK、それぞれ。臨界ダストサイズs•〜0.1 − 10 mmの場合、
サブケプラーの向かい風による空気力学的エネルギー損失は、半径方向の風によるエネルギーゲインを正確に打ち消し、
ディスク内のほこり。このプロセスにより、システム内にほこりがたまり、ディスクの金属性Zが成長します。
時間。このダストとガスの比率の段階的な強化により、ソリッドサブディスクがミッドプレーンにますます近づき、
スケールの高さh•が重力安定性のしきい値（Q•。1）を下回ると、ソリッドサブディスクの外側の領域
mから10＾19 kgの微衛星の群れに断片化。衛星の胚の降着は、ペアワイズ衝突を介して進行します
重力フォーカシングによって。衛星がかなりの後流を発生させるのに十分なほど大きくなると、集積は終了します
惑星の円盤の中で。この時点で、長距離ディスク主導の移行が行われ、新しく形成されたオブジェクトが登場します。
磁気圏空洞に向かって。


図2.モデルの惑星周囲円盤の面密度プロファイル。 正確な解（式7）–対応定数M˙の減少に対応するα-モデルは、
パープルライン。 このソリューションに適合する指数−5/4べき法則（式12）は濃いオレンジ色の破線で描かれています。
参照面密度Σ0= 4,000 g / cm2 参照半径r0 = 0.1RHは細い点線で示されています。（垂直方向に等温であると想定される）の温度プロファイル
ディスクは図の上部に色で表示されていますバー。 重要なのは、私たちのモデルのコンテキスト内では、氷の凝縮がその後に続くのに十分なほど温度が低いことです。
r＆r0。 ディスクの内側の端はサイズによって決定されます メイジスフェアキャビティ（式2）のRT〜5 RJup。


図3.周縁星雲のアスペ​​クト比。
私たちのモデルの枠組みの中で、垂直方向の厚さ
ガス状ディスクの温度は、単にその温度構造を反映している
（h / r = cs / vK via√T）。粘性エネルギーの散逸は惑星の照射（式11）よりも支配的であるため、
温度プロファイル自体は、ディスク内の乱流加熱を黒体放射損​​失と同等にすることによって決定されます
その表面に。上部のパネルには、星雲のガス状成分（式10）
紫色の実線。私たちの目的のために、軌道半径によるh / rの小さな変動を無視して、
一定のアスペクト比を持つディスク。私たちの採用価値のh / r = 0.1は、濃いオレンジ色の破線で表示されます
トップパネル。ダストレイヤーのアスペクト比-計算
Scが1の質量のないトレーサー粒子の限界（式22）–が上部パネルに黒い曲線で表示されます。
下のパネルは、さまざまなディスクの金属性に対する固体サブディスクのアスペクト比h•/ rを示し、
ダストディスクの厚さのエネルギー抑制（式29）。乱流攪拌のかつてのエネルギー制限はダスト層のh、/ r h / rが考慮されます。
さらに、h•/ r ∝ 1 /であることに注意してください。√Z、およびZおよび0.1の場合は、h•/ rです。 10−3


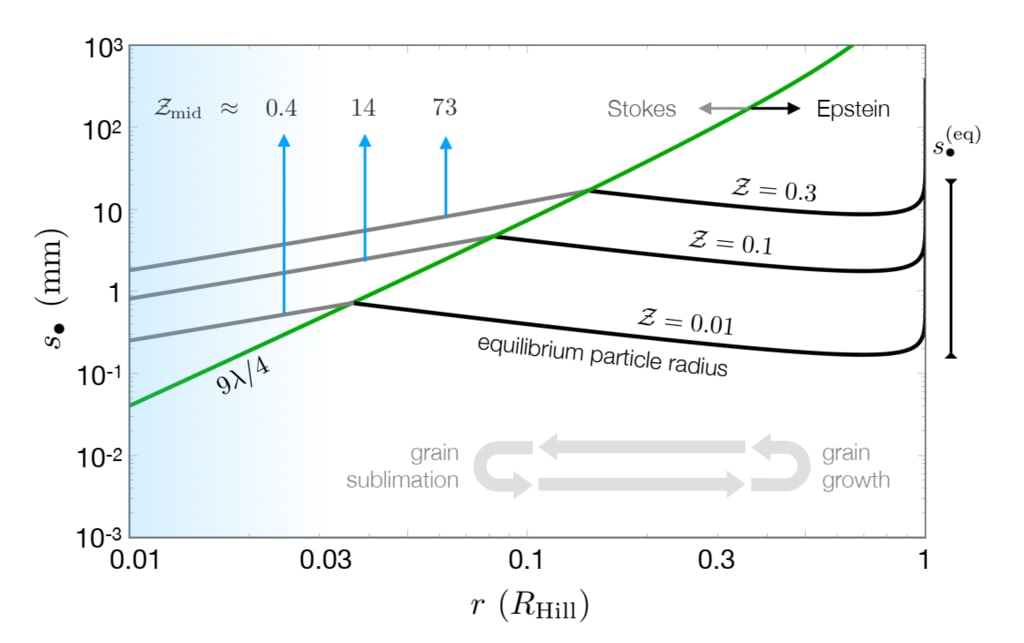
図4.平衡ダスト粒子半径、s（eq）•、関数として平面から中心までの距離。半径が制限されたダスト粒子
指定された範囲（つまり、s•〜0.1 − 10 mm;式19）おかげで、惑星の円盤内に閉じ込められたままになります
空力抵抗とラジアル上昇気流の間のバランスに。
Z = 0.01、0.1、および0.3のグローバルディスク金属性に対応する平衡曲線（これは、中央平面に変換されます）
Zmidの金属性度=それぞれ0.4、14、および74;式30）を参照してください。図に描かれている緑の線
エプスタイン体制とストークス体制の間の移行をマーク
ドラッグ：（s•）t =9λ/ 4、ここでλは平均自由行程を表す
ガス分子の。導出されたダスト平衡は、ドラッグのエプスタイン体制における一定の粒子サイズ
ストークス体制。直接モデル化されていませんが、おそらくダストの成長/昇華サイクルは、s•の変調において重要な補助的な役割を果たすことができること。特に、
sが（eq）•は、rの減少関数です。エプスタイン体制、外側のディスクでの粒子成長は軌道崩壊。逆の効果は小さな軌道半径で起こります、
アイスラインの内側にある氷のような穀物の昇華が原因 粒子サイズが平衡値を下回ると排出されます
粒の成長が一度起こることができる外側の固体材料
再び、それによってs•〜sを維持（eq）•平均して。