太陽風は、水星のジャイアントインパクト後の破片の再付着を防ぎます

水星のジャイアントインパクト後の破片は太陽風で軌道を変えられて水星の重力圏に戻れない説です。飛ばされた地殻とマントルが降着しないと鉄のコアばかりの水星の出来上がりということ。以下、機械翻訳。
太陽風は、水星のジャイアントインパクト後の破片の再付着を防ぎます
（2020年2月18日に提出）
惑星水星は異常に大きな鉄心とそれに対応する高いかさ密度を持っています。このような大きな鉄含有量を説明するために、多くの仮説が提案されています。長い間考えられていたのは、水星がかつて大きなケイ酸塩マントルを持っていたということです。マントルは、太陽系の歴史の初期にジャイアントインパクトによって取り除かれました。このアイデアの中心的な問題は、水星から放出された物質が通常、短い（〜Myr）タイムスケール後に惑星に再付着することです。ここでは、原始太陽風が放出された破片に十分な抗力を与え、惑星表面に再び影響を与える前に水星を横断する軌道からそれらを取り除くことを示します。具体的には、若い太陽はより強い風、速い回転、強い磁場を持っている可能性がありました。巨大な衝撃の時間に応じて、この風に伴うラム圧は、放出されたデブリのサイズに応じて、サブマイアタイムスケールで粒子を太陽系に向かって、または太陽に向かって押し出します。したがって、ジャイアントインパクト仮説は、水星と太陽系外惑星、特に強風の若い星に近い惑星の両方で、惑星のマントルを除去するための実行可能な経路のままです。
図1.この研究で検討した物理シナリオの概略図。 材料は、ジャイアントインパクトに続いて水星から発射されます（1）。
この物質は最初、水星の軌道を横切る外側の赤い軌道（灰色の楕円）をたどります。 太陽風プラズマ引き込みによる抵抗粒子の軌道からの角運動量（2）により、軌道は時間とともに太陽に向かって内側に螺旋状になり（3）、最終的には
水星の軌道（4）、再降着を禁止します。 右側のズームインは、初期軌道を規定するために使用される座標フレームを示します
N体シミュレーション（セクション5）での衝突破片の検出。 インスパイラル依存のタイムスケールは、粒子半径とともに線形に増加します。
全体で半径1 cmが想定されています（粒子サイズについてはセクション6.2を参照）


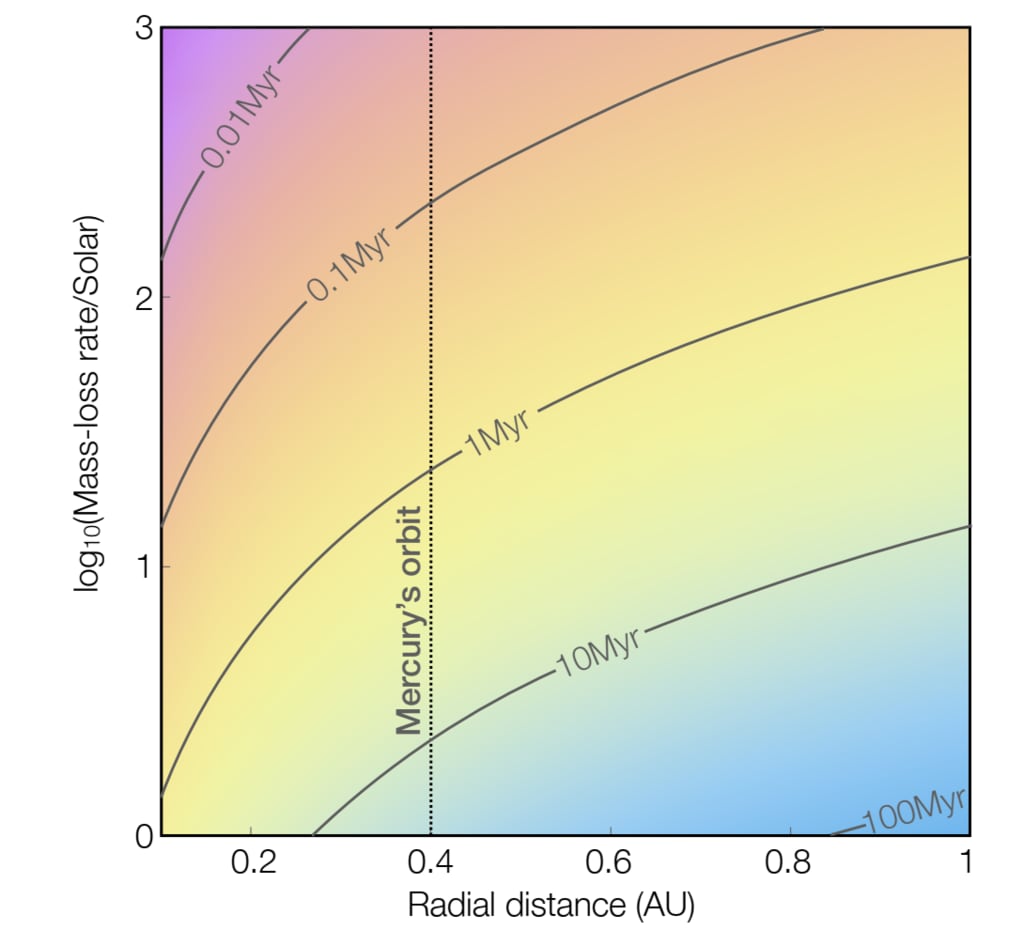
図2.—の場合の軌道移行タイムスケールの輪郭
純粋に放射状の風（vφ= 0）、背景色はドリフトタイムスケールのグラデーション。 太陽風の大きさが与えられます
現代の太陽の質量損失の単位でy軸に。 軌道水星の（〜0.4 AU）は破線で示され、1 Myr
ドリフトタイムスケールの輪郭は灰色でマークされています。 質量損失の値＆10倍は1cmの軌道移動を引き起こすのに十分です
放出物の再付着を防ぐ、1 Myrタイムスケールの粒子水星の表面に。


図3.—半径方向（上）および方位角（下）の速度
3つの異なる時間で計算された太陽風-3 Myr、10 Myと30Myr。 地域と時間を示すために、方位角速度をケプラー軌道速度と比較します
太陽風が粒子を加速するように作用する場所（vφがケプラーを超える場所）。 30 Myrに続く、方位角速度
ケプラー速度と動径速度の両方を十分下回って、最終的には無視できるようになります。 常に、方位角速度は恒星表面から着実に上昇し、最終的には
弱まる磁気応力による大きな距離（Weber＆デイビス196


図4-打ち上げの関数としての太陽風による半長軸（左）と離心率（右）の進化的タイムスケール
水星の軌道に対する角度。 初期（3マイル）および後期（30マイル）の段階での2つの発射速度（4 km / sおよび15 km / s）を示します。 すべてのために
パラメータ、進化のタイムスケールは1 Myrよりも短く、再付着する前に効率的に除去されることを示します。


図5.— 1 cmサイズの粒子の軌道進化タイムスケール
のソリューションから生じる太陽風の作用の下でWeber-Davisモデル（赤）–点線は
外側への移動と実線は、内側への移動（軌道崩壊）の時間を示します。 また、純粋に放射状の太陽風（青）とPoyntingRobertsonのドラッグ（黒）に関連付けられたドラッグタイムスケールもプロットされています。

6.議論と結論
半分析理論の組み合わせによる
数値シミュレーションでは、ドラッグが初期の太陽の風に関連付けられている可能性があり、cmサイズの粒子が
<1 Myrタイムスケール。前の研究では、水星の先祖への巨大な影響は、
マントルを太陽中心軌道に入れ、そこで物質を凝縮して〜cmサイズの物体にします。したがって、太陽風の追加により、
当時の今日よりも大幅に大きくなっています 影響、これの多くが排出される可能性を減らす材料は水星に再付着します。
再降着の問題に対する代替ソリューション提案されています。ポインティング・ロバートソン効果、
例は、太陽の影響に最も類似しています 風（Burns et al。1979）。前の仕事はそれを示しました
ポインティング・ロバートソンのドラッグに関連付けられたタイムスケール ノミナルパラメーターの場合、実際には10 Myrよりも短くなります。
解決策としてのポインティング・ロバートソン抵抗の批判の光学的深さが
破片のリングと称されるものは、単一性を超える場合があります（グラッドマン＆Coffey 2009）。これにより、除去のタイムスケールが長くなり、再付着の時間が長くなります。
この文脈における太陽風の利点は、潜在的に10〜100倍強いため、太陽風イオンの侵入が材料の密なリングの存在、複数存在します
リングを削除する軌道減衰時間。にさらに、リング粒子の微分非歳差歳差運動リングにゼロ以外のスケールの高さを与えます
自己シールドの度合いを減らします。自己シールドの問題は、フォローアップ作業で調査する価値があります。