今回はExcelのデータ分析(フーリエ解析)機能を使いタイヤ編(17)で解析したフーリエ係数、振幅、位相を確認します。
初めてExcelでデータ分析を使用する場合は、予め【ファイル】タブの【オプション】→【アドイン】→【設定】をクリックすると、
【有効なアドイン】画面が表示されますので、【分析ツール】にチェックを入れてOKボタンを押してからご使用下さい。
今回のお話しではExcel-VBAは用いませんが、FFT解析等のプログラム制作に挑戦すると言う方は、
【分析ツール・VBA】にもチェックを入れて下さい。
(注記:Excelバージョンにより異なる場合が有りますのでマイクロソフトのサポート等でご確認下さい)
今回も新しいExcelシートを用意して説明します。
前回と同様にシートの追加は見出し横の⊕マークをクリックするとSheet3が用意されます。
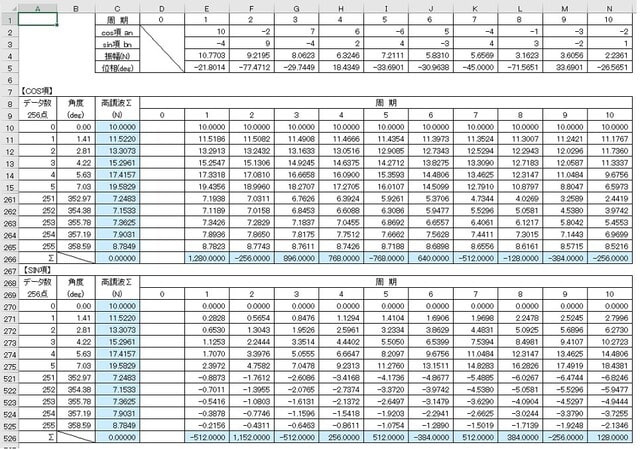
参考にExcelシートを添付します

(注記:一部の行はグループ化後、非表示となっています)
A10セルにデータ数を入力します。
A10セルに式 =Sheet1!$A4 と入力し、 (注記 :合成波形データを作成したExcelシートに名称を付けていない場合)
A10セル右下のポイントをクリックしながらA265セルまでマウスを移動すると自動で式と数値が入力されます。
B10セルに角度を入力します。
B10セルに式 =Sheet1!$B4と入力し、
B10セル右下のポイントをクリックしながらB265セルまでマウスを移動すると自動で式と数値が入力されます。
C10セルに合成波形データを入力します。
C10セルに式 =Sheet1!$BA4と入力し、
C10セル右下のポイントをクリックしながらC265セルまでマウスを移動すると自動で式と数値が入力されます。
ここまでは前回と同じ手順で合成波形データを貼り付ける事が出来ました。
ここからはExcelのデータ分析機能(フーリエ解析)を使って解析を行います。
【データ】タブをクリック、リボンの中の【分析】→【データ分析】ボタンをクリックします。
データ分析画面が表示されるので【分析ツール(A)】内の【フーリエ解析】をクリックしてOKボタンを押すとフーリエ解析画面が表示されます。
次に解析データの範囲を指定します。
C10セルをクリックしてC265セルまでマウスを移動すると【入力範囲(I)】に選択したセル範囲が自動入力されます。
次に【出力オプション】の【出力先(O)】をクリックして解析結果を表示させたいセル範囲を決定します。
ここではE10セルをクリックしてOKボタンを押すとE10セル~E265セルに解析結果が表示されます。
解析結果を見ると、
何じゃこりゃ~! と思うでしょ! (注記:ここは松田優作さんになり切って言って見ましょう! )
何やら数式の様な結果に i と言う文字があ~りませんか? (注記:ここはチャーリー浜さんになり切って言って見ましょう! )
なんでやねん! (注記:孤独のグルメSeason6 第1話 大阪出張編で池乃めだかさんがこれ言っとけば大体OKらしい! )
ほんまかいな! 兄ちゃん!
もうええわ!
お後が宜しい様で! ♬ チャカチャカ~ ドどん ♬
そうなのです。
i が入っている数式と言えば複素数です。
a、bを実数とするとき、a+bi の形の数を複素数と言って、aを実部、bを虚部、iを虚数単位と言い i ² = -1であると定義します。
高校の数学Ⅰ、数学ⅡB、数学Ⅲの何れかで習いましたよね! (注記 : コロコロと履修学年が替わるので判りません)
凡人の私には二乗して答えが -1 になるなんて良く判りませんが、
ここでは複素数を取り入れたフーリエ級数で考えるとcos nxやsin nxを用いた展開式では無く、
複素指数関数eⁱⁿを使った式で展開(高速FFT解析)できるので解析結果を早く導き出せると言う一般的な内容でお茶を濁します。
詳しく知りたい方は、複素数、オイラーの公式、ド・モアブルの定理、複素フーリエ級数を大学基礎教養サイトや受験サイト等で確認して下さいネ!
i、うん?「愛」と書いて「めぐみ」と読む! (注記:ここは田村正和さんになり切って言ってみましょう! ちょっと鼻が詰まった感じでネ!)
歳が知れるわ!!
もうええちゅうに!
ごめんチャイ!
ここまで来たら後はセルに関数式を入力して行きます。
フーリエ係数an(実数部)を求めます。
F10セルに =IMREAL($E10) / 128と入力します。 (注記:関数 IMREALは x+yiの形式で指定された複素数の実数係数を返します)
セル右下のポイントをクリックしてE265セルまでマウスを移動させると自動計算されます。
E10セル~E20セルには高調波1次から10次成分までのフーリエ係数anが計算されました。
フーリエ係数bn(虚数部)を求めます。
F10セルに =-IMAGINARY($E10) / 128と入力します。 (注記:関数 IMAGINARYは x+yiの形式で指定された複素数の虚数係数を返します)
セル右下のポイントをクリックしてF265セルまでマウスを移動させると自動計算されます。
F10セル~F20セルには高調波1次から10次成分フーリエ係数bnが計算されました。
振幅(振幅スペクトル)を求めます。
H10セルに =SQRT(POWER($F10,2) + POWER($G10,2))と入力します。 (注記:関数 SQRTは正の平方根を返し、関数 POWERは数値のべき乗を返します)
セル右下のポイントをクリックしてH265セルまでマウスを移動させると自動計算されます。
H10セル~H20セルには高調波1次から10次成分までの振幅(N)が計算されました。
位相(位相スペクトル)を求めます。
I11セルに =ATAN($G11 / $F11と入力します。 (注記:関数 ATANは数値のアークタンジェント (逆正接) を返します)
セル右下のポイントをクリックしてI265セルまでマウスを移動させると自動計算されます。
I11セル~I20セルには高調波1次から10次成分までの位相(rad)が計算されました。
単位がラジアン(rad)なので度(deg)に変換します。
J11セルに =DEGREES($I11)と入力します。 (注記:関数 DEGREESはラジアン(rad)を度(deg)に変換します)
セル右下のポイントをクリックしてJ265セルまでマウスを移動させると自動計算されます。
以上でデータ分析機能を使ったフーリエ解析は終わりです。
DFT解析で計算した数値と比較して下さい。
同じ数値になっていると思います。
違う場合は入力した式と数値を確認して下さい。
ここで振幅の数値を見るとデータ数の1~10までと、データ数255~246までの数値が同じになっていると気づくでしょ!
参考にデータ数と振幅のグラフを添付します。

今回は周波数(Hz)で計算していないので判り辛いと思いますが、ちょうどデータ数128の位置を境に対称となっています。
この位置が周波数で言うナイキスト周波数に相当するポイントです。
今回のケースで言うと高調波128次(高調波256次の半分)以下では、離散フーリエの解析結果に信頼性が認められますが、
解析前のデータにそれ以上の高い高調波が含まれたデータの場合、解析結果の信頼性は低下すると考えます。
よって、解析前にフィルター等で高い周波数成分を小さくするか、サンプリング周波数をその高調波より2倍以上高く設定しなければなりません。
詳しく知りたい方は、ナイキスト周波数、サンプリング周波数に付いて大学基礎教養サイトで確認して下さい。
タイヤ編(15)から今回までフーリエ解析に付いての概略お話ししました。
ユニフォーミティ装置で測定される1次、2次、3次成分等の振幅、位相はこの様にして解析されています。
(注記:実際の測定では高速フーリエ解析が主流です)
尚、位相に関してはタイヤ+ホイールAssyを取付ける回転軸の末端等に取付けられている回転センサーの原点を利用したり、
プログラム上で原点を設定してエアバルブの位置やホイール取付穴等を0基準と定めて測定します。
最後に今回作成した高調波1次~10次までの波形グラフと、それらを合成した波形グラフを参考に添付します。
高調波1次~10次成分波形

高調波1次~10次成分合成波形

最後に私は信号処理の専門家では有りませんので不適内容、誤記等ございましたらお知らせ下さい。
初めてExcelでデータ分析を使用する場合は、予め【ファイル】タブの【オプション】→【アドイン】→【設定】をクリックすると、
【有効なアドイン】画面が表示されますので、【分析ツール】にチェックを入れてOKボタンを押してからご使用下さい。
今回のお話しではExcel-VBAは用いませんが、FFT解析等のプログラム制作に挑戦すると言う方は、
【分析ツール・VBA】にもチェックを入れて下さい。
(注記:Excelバージョンにより異なる場合が有りますのでマイクロソフトのサポート等でご確認下さい)
今回も新しいExcelシートを用意して説明します。
前回と同様にシートの追加は見出し横の⊕マークをクリックするとSheet3が用意されます。
参考にExcelシートを添付します

(注記:一部の行はグループ化後、非表示となっています)
A10セルにデータ数を入力します。
A10セルに式 =Sheet1!$A4 と入力し、 (注記 :合成波形データを作成したExcelシートに名称を付けていない場合)
A10セル右下のポイントをクリックしながらA265セルまでマウスを移動すると自動で式と数値が入力されます。
B10セルに角度を入力します。
B10セルに式 =Sheet1!$B4と入力し、
B10セル右下のポイントをクリックしながらB265セルまでマウスを移動すると自動で式と数値が入力されます。
C10セルに合成波形データを入力します。
C10セルに式 =Sheet1!$BA4と入力し、
C10セル右下のポイントをクリックしながらC265セルまでマウスを移動すると自動で式と数値が入力されます。
ここまでは前回と同じ手順で合成波形データを貼り付ける事が出来ました。
ここからはExcelのデータ分析機能(フーリエ解析)を使って解析を行います。
【データ】タブをクリック、リボンの中の【分析】→【データ分析】ボタンをクリックします。
データ分析画面が表示されるので【分析ツール(A)】内の【フーリエ解析】をクリックしてOKボタンを押すとフーリエ解析画面が表示されます。
次に解析データの範囲を指定します。
C10セルをクリックしてC265セルまでマウスを移動すると【入力範囲(I)】に選択したセル範囲が自動入力されます。
次に【出力オプション】の【出力先(O)】をクリックして解析結果を表示させたいセル範囲を決定します。
ここではE10セルをクリックしてOKボタンを押すとE10セル~E265セルに解析結果が表示されます。
解析結果を見ると、
何じゃこりゃ~! と思うでしょ! (注記:ここは松田優作さんになり切って言って見ましょう! )
何やら数式の様な結果に i と言う文字があ~りませんか? (注記:ここはチャーリー浜さんになり切って言って見ましょう! )
なんでやねん! (注記:孤独のグルメSeason6 第1話 大阪出張編で池乃めだかさんがこれ言っとけば大体OKらしい! )
ほんまかいな! 兄ちゃん!
もうええわ!
お後が宜しい様で! ♬ チャカチャカ~ ドどん ♬
そうなのです。
i が入っている数式と言えば複素数です。
a、bを実数とするとき、a+bi の形の数を複素数と言って、aを実部、bを虚部、iを虚数単位と言い i ² = -1であると定義します。
高校の数学Ⅰ、数学ⅡB、数学Ⅲの何れかで習いましたよね! (注記 : コロコロと履修学年が替わるので判りません)
凡人の私には二乗して答えが -1 になるなんて良く判りませんが、
ここでは複素数を取り入れたフーリエ級数で考えるとcos nxやsin nxを用いた展開式では無く、
複素指数関数eⁱⁿを使った式で展開(高速FFT解析)できるので解析結果を早く導き出せると言う一般的な内容でお茶を濁します。
詳しく知りたい方は、複素数、オイラーの公式、ド・モアブルの定理、複素フーリエ級数を大学基礎教養サイトや受験サイト等で確認して下さいネ!
i、うん?「愛」と書いて「めぐみ」と読む! (注記:ここは田村正和さんになり切って言ってみましょう! ちょっと鼻が詰まった感じでネ!)
歳が知れるわ!!
もうええちゅうに!
ごめんチャイ!
ここまで来たら後はセルに関数式を入力して行きます。
フーリエ係数an(実数部)を求めます。
F10セルに =IMREAL($E10) / 128と入力します。 (注記:関数 IMREALは x+yiの形式で指定された複素数の実数係数を返します)
セル右下のポイントをクリックしてE265セルまでマウスを移動させると自動計算されます。
E10セル~E20セルには高調波1次から10次成分までのフーリエ係数anが計算されました。
フーリエ係数bn(虚数部)を求めます。
F10セルに =-IMAGINARY($E10) / 128と入力します。 (注記:関数 IMAGINARYは x+yiの形式で指定された複素数の虚数係数を返します)
セル右下のポイントをクリックしてF265セルまでマウスを移動させると自動計算されます。
F10セル~F20セルには高調波1次から10次成分フーリエ係数bnが計算されました。
振幅(振幅スペクトル)を求めます。
H10セルに =SQRT(POWER($F10,2) + POWER($G10,2))と入力します。 (注記:関数 SQRTは正の平方根を返し、関数 POWERは数値のべき乗を返します)
セル右下のポイントをクリックしてH265セルまでマウスを移動させると自動計算されます。
H10セル~H20セルには高調波1次から10次成分までの振幅(N)が計算されました。
位相(位相スペクトル)を求めます。
I11セルに =ATAN($G11 / $F11と入力します。 (注記:関数 ATANは数値のアークタンジェント (逆正接) を返します)
セル右下のポイントをクリックしてI265セルまでマウスを移動させると自動計算されます。
I11セル~I20セルには高調波1次から10次成分までの位相(rad)が計算されました。
単位がラジアン(rad)なので度(deg)に変換します。
J11セルに =DEGREES($I11)と入力します。 (注記:関数 DEGREESはラジアン(rad)を度(deg)に変換します)
セル右下のポイントをクリックしてJ265セルまでマウスを移動させると自動計算されます。
以上でデータ分析機能を使ったフーリエ解析は終わりです。
DFT解析で計算した数値と比較して下さい。
同じ数値になっていると思います。
違う場合は入力した式と数値を確認して下さい。
ここで振幅の数値を見るとデータ数の1~10までと、データ数255~246までの数値が同じになっていると気づくでしょ!
参考にデータ数と振幅のグラフを添付します。

今回は周波数(Hz)で計算していないので判り辛いと思いますが、ちょうどデータ数128の位置を境に対称となっています。
この位置が周波数で言うナイキスト周波数に相当するポイントです。
今回のケースで言うと高調波128次(高調波256次の半分)以下では、離散フーリエの解析結果に信頼性が認められますが、
解析前のデータにそれ以上の高い高調波が含まれたデータの場合、解析結果の信頼性は低下すると考えます。
よって、解析前にフィルター等で高い周波数成分を小さくするか、サンプリング周波数をその高調波より2倍以上高く設定しなければなりません。
詳しく知りたい方は、ナイキスト周波数、サンプリング周波数に付いて大学基礎教養サイトで確認して下さい。
タイヤ編(15)から今回までフーリエ解析に付いての概略お話ししました。
ユニフォーミティ装置で測定される1次、2次、3次成分等の振幅、位相はこの様にして解析されています。
(注記:実際の測定では高速フーリエ解析が主流です)
尚、位相に関してはタイヤ+ホイールAssyを取付ける回転軸の末端等に取付けられている回転センサーの原点を利用したり、
プログラム上で原点を設定してエアバルブの位置やホイール取付穴等を0基準と定めて測定します。
最後に今回作成した高調波1次~10次までの波形グラフと、それらを合成した波形グラフを参考に添付します。
高調波1次~10次成分波形

高調波1次~10次成分合成波形

最後に私は信号処理の専門家では有りませんので不適内容、誤記等ございましたらお知らせ下さい。