▶賢者の解答だったので備忘録として残します。
知恵袋:https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q10291893330
【問題】図(a)から図(b)の回路に変換する際、R1を流れるI1とR2を流れるI2が図(a)と図(b)でそれぞれ変化しないようにしたい。 これを達成できるExとRxをそれぞれE、R3およびR4を用いて示せ。

≫fried_turnipさんの回答を元にした、私なりの解答です↓
▼等価性より(相反性?) 図(a)、図(b)においてVa=Vbが成立する為には、図1=図2であればよい。

▼ミルマンの定理で解く R1を流れるI1とR2を流れるI2が図(a)と図(b)でそれぞれ変化しない様にしたい。と云う事はVa=Vbである必要がある。つまりVa=Vbが条件なので、この条件を下に解析し易い様に変形すると…

▼等価性 Va=Vbなら、回路の等価性より (a-3)=(b-2) と云える。つまり(a-3)と(b-1)を入れ替えて元の回路に戻してもI1,I2に影響を与える事がないので(a-3)と(b-1)は等価交換できる、と云う事です。


















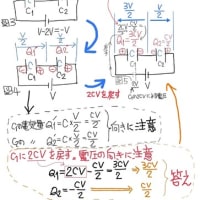
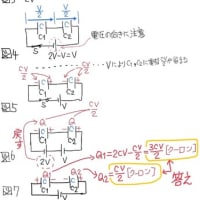
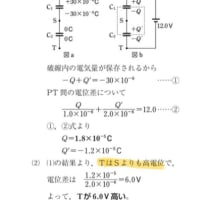
※コメント投稿者のブログIDはブログ作成者のみに通知されます