2 動的解析のために
さて、尾形先生の参考書に沿ってすすめよう。
2章では、動的システム解析の準備として、部分分数展開を取り上げている。読者は、古典制御の知識があるものとしているのであるが、本ブログでは少々それについて説明をしていこうと思う。
線形システム つまり 重ねあわせができるシステムにおいては伝達関数は、部分分数によって表すことができる。
勉強であるから、以後は線形システムをまず扱う。
入力があって出力(応答)がある。
例えば、筆者の専門から言えば、地震動がある。
建物に、地震動が入力すると、出力としては 建物の揺れが起きる。これが建物の応答である。建物というシステムが、線形であれば、おなじような地震動を入力するといつも同じ応答が起こる。
これを表すのに伝達関数というのを使う。つまり、入力から伝達されて応答になるというところを関数として表すのである。
sをラプラス演算子として
部分分数表現は
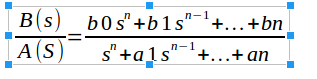
といった形をとる。
例えばMATLABだと
伝達関数はnum=[2 5 3 6],den=[1 6 11 6]として、伝達関数を表すが、scilabでは
直接書く。
-->s=poly(0,'s');
-->H=[(2*s^3+5*s^2+3*s+6)/(s^3+6*s^2+11*s+6)]
H =
2 3
6 + 3s + 5s + 2s
----------------
2 3
6 + 11s + 6s + s
そして 部分分数展開は
-->pfss(H)
ans =
ans(1)
- 6
-----
3 + s
ans(2)
3
-----
1 + s
ans(3)
- 4
-----
2 + s
ans(4)
2.
でこれが直達項
となる。
さて、伝達関数表現と状態空間表現とはお互いに等価である。というか、表現を変えただけであるということでお互いに変換が可能である。
状態空間表現とは

のマトリクス表現であり
これの伝達関数は
となる。
さて、やってみよう。
-->H=[(10*s+10)/(s^3+6*s^2+5*s+10)]
H =
10 + 10s
----------------
2 3
10 + 5s + 6s + s
これを状態空間表現にすると、各マトリクスは
以下のようになる
-->tf2des(H)
ans =
ans(1)
!des A B C D E !
ans(2):これがA
0.8 3.6 1.277D-15
- 1.8444444 - 5.6765432 1.1042311
- 1.4037538 2.3340685 - 1.1234568
ans(3):これがB
0.
- 4.4444444
0.4969040
ans(4):これがC
- 0.625 - 1.388D-17 - 1.943D-16
ans(5):これがD
0.
ans(6):これがE(通常いらないが) E dx/dt=Ax+Bu のEというマトリクス 通常は単位行列
1. 0. 0.
0. 1. 0.
0. 0. 1.
として求まった。もう少し本当は綺麗な数になるのだが。。。
さて、尾形先生の参考書に沿ってすすめよう。
2章では、動的システム解析の準備として、部分分数展開を取り上げている。読者は、古典制御の知識があるものとしているのであるが、本ブログでは少々それについて説明をしていこうと思う。
線形システム つまり 重ねあわせができるシステムにおいては伝達関数は、部分分数によって表すことができる。
勉強であるから、以後は線形システムをまず扱う。
入力があって出力(応答)がある。
例えば、筆者の専門から言えば、地震動がある。
建物に、地震動が入力すると、出力としては 建物の揺れが起きる。これが建物の応答である。建物というシステムが、線形であれば、おなじような地震動を入力するといつも同じ応答が起こる。
これを表すのに伝達関数というのを使う。つまり、入力から伝達されて応答になるというところを関数として表すのである。
sをラプラス演算子として
部分分数表現は
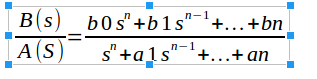
といった形をとる。
例えばMATLABだと
伝達関数はnum=[2 5 3 6],den=[1 6 11 6]として、伝達関数を表すが、scilabでは
直接書く。
-->s=poly(0,'s');
-->H=[(2*s^3+5*s^2+3*s+6)/(s^3+6*s^2+11*s+6)]
H =
2 3
6 + 3s + 5s + 2s
----------------
2 3
6 + 11s + 6s + s
そして 部分分数展開は
-->pfss(H)
ans =
ans(1)
- 6
-----
3 + s
ans(2)
3
-----
1 + s
ans(3)
- 4
-----
2 + s
ans(4)
2.
でこれが直達項
となる。
さて、伝達関数表現と状態空間表現とはお互いに等価である。というか、表現を変えただけであるということでお互いに変換が可能である。
状態空間表現とは

のマトリクス表現であり
これの伝達関数は
となる。
さて、やってみよう。
-->H=[(10*s+10)/(s^3+6*s^2+5*s+10)]
H =
10 + 10s
----------------
2 3
10 + 5s + 6s + s
これを状態空間表現にすると、各マトリクスは
以下のようになる
-->tf2des(H)
ans =
ans(1)
!des A B C D E !
ans(2):これがA
0.8 3.6 1.277D-15
- 1.8444444 - 5.6765432 1.1042311
- 1.4037538 2.3340685 - 1.1234568
ans(3):これがB
0.
- 4.4444444
0.4969040
ans(4):これがC
- 0.625 - 1.388D-17 - 1.943D-16
ans(5):これがD
0.
ans(6):これがE(通常いらないが) E dx/dt=Ax+Bu のEというマトリクス 通常は単位行列
1. 0. 0.
0. 1. 0.
0. 0. 1.
として求まった。もう少し本当は綺麗な数になるのだが。。。

















※コメント投稿者のブログIDはブログ作成者のみに通知されます