パン、アトラス、ダフニスの飾りの付いた赤道山脈の降着

目玉焼きみたいなアトラス、メロンパンに餃子の羽が付いたようなパンとユニークな土星の衛星。リングの粒子が衛星の重力で衛星に落下し自転による遠心力で赤道に集まるのかと軽く考えていたが、降着の時の運動エネルギーが自転速度に影響し、ロシュローブの形も土星の影響で歪。以下、機械翻訳。

パン、アトラス、ダフニスの飾りの付いた赤道山脈の降着
2020年7月26日に提出
土星の環の材料から土星の衛星パン、アトラス、ダフニスに装飾的な尾根が付着するシナリオを探索します。着陸した材料からのトルクが、通常は潮汐ロックを維持する土星からの潮汐トルクを超えない場合、リング材料からの複雑な形状の尾根の降着が可能になるはずです。これにより、赤道の尾根成長の最大降着率と最小継続時間が制限されます。最初に円軌道にあるリング材料から、円軌道、傾斜軌道、または偏心軌道上の衛星に着陸した尾根の経度分布を調べます。形状の変化またはディスクエッジの表面密度プロファイルにより、衛星の赤道尾根の異なる場所で衛星に影響を与えることができるため、衛星の形状が変化したり、ディスクエッジの表面密度プロファイルが原因で衛星が潮汐で再整列したりすると、傾斜した尾根が隆起する可能性があります。 。非対称なギャップからの降着がアトラスの赤道海嶺の不況の原因である可能性があることがわかりました。ヒルの離心率と同様の軌道の離心率での非対称ギャップからの降着は、パンで見られるように、複数の葉の降着を可能にするかもしれません。おそらく関連する2つのシナリオは、観賞用の赤道の尾根の成長を約束しています。衛星はリングを通って移動し、そのギャップを狭め、降着を容易にします。衛星の軌道偏心は、別の衛星との軌道共鳴により増加する可能性があります。
キーワード：土星、衛星–回転ダイナミクス–衛星、ダイナミクス

図1：月のパン、アトラス、ダフニスのグレースケール画像
ISS（イメージングサイエンスサブシステム）でカッシーニミッションフライバイ後半に取得。 画像番号はN1867604669です。
パン、アトラスにはN1870699120、ダフニスにはN1863267232。 これら
画像は同じ縮尺で表示されていません。 経度には次のラベルを付けました
トーマスのワイヤーフレーム図を使用したパンとアトラスの青い線
とガイドとしてヘルフェンシュタイン（2020）。 これらは図に示されています
7と8、それらの形状モデルから派生。 慣例として、0◦衛星の経度は土星に面し、90◦Wは方向に面しています
衛星の軌道運動の。 パンに「N」のラベルが付いた北極アトラスは、2つの青い線が交差する場所にあります。
ボトム2つのパネルには、ダフニスの同じ2つの画像が表示されますが、異なる
対比。 下の画像は、かすかなWispの内部をよりよく示しています
ダフニスによって摂動されたリングエッジ。 これらの衛星はほぼロシュ地域を埋める。 体軸比を表1に示します。


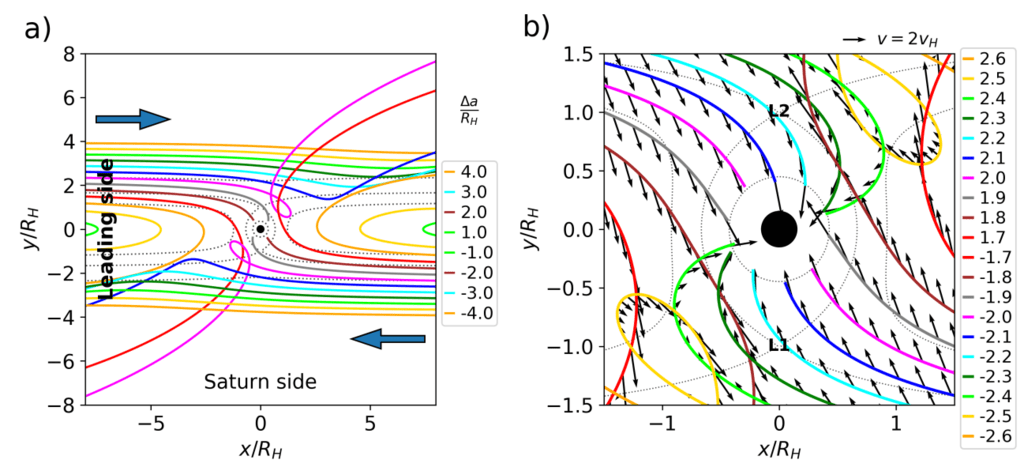
図2：惑星の円軌道にある衛星と共に回転するフレーム内の粒子軌道をテストします。衛星の重心が表示されます
各プロットの中央に黒い点があります。 x軸とy軸は丘の半径の単位であり、衛星は原点を中心とします。惑星
負のy軸上にあります。衛星の先頭は左側です。テスト粒子はゼロ偏心度と傾斜角で開始されました
中央惑星の周りの軌道の異なる軌道準主軸で。軌道は衛星と惑星の質量比で計算されました
µ = 10-11ですが、RHの単位でのこれらの軌道の形態は、この比が低い限り、質量比µに依存しません。各
テスト粒子の軌道は別の色の線で示され、キーのRHの単位からRHの単位でその初期の準主軸によってラベルが付けられています
衛星の軌道。灰色の点線の輪郭は、有効電位Veffのレベルを示しています（式7を参照）。有効ポテンシャルの鞍点
L1とL2のラグランジュポイントがあり、L1は惑星に面する下側にあります。 a）テスト粒子の軌道を示します。濃い青
矢印は、回転フレーム内の軌道の初期運動方向を示します。 b）衛星に近い領域を示すことを除いて、a）と同様
と速度ベクトル。速度ベクトルは、周回する粒子と衛星の瞬間速度の差です。上のベクトル
右上は、ヒルの速度vHの2倍の大きさの速度を示しています。衛星への粒子衝突サイトのテストは、それらの初期に依存します
準長軸とヒルの球体のどのくらいが衛星で満たされているか。最初は平面の円軌道上のテスト粒子は、
衛星の赤道上のほぼすべての場所で衛星に影響を与えます。


図3：テスト粒子軌道の角度と接線速度。
上部パネルには、衛星/惑星から測定された衝突角度が表示されます
ライン（+ y軸）、テスト用の衛星の中心からの半径の関数として
図2bに示す粒子軌道。この角度が影響を決定します
降着物質の経度（衛星の赤道上）（図を参照）
4）。下のパネルは、衛星からの半径の関数と同じ軌道で、単位は
ヒル速度vHの接線速度コンポーネント時間
半径は、降着物質のスピン角運動量を与えます。
vθの正の値を持つ付着した材料は、
衛星。キーは、初期テスト粒子間の異なる∆aを示します
丘の半径の単位での軌道の半長軸と衛星の主軸
RH。外側の軌道から発生した粒子のみを表示します
衛星の軌道。粒子は衛星の軌道の内部から発生します
同じ角度から180度回転した衝突角度がある| ∆a |だが
衛星の軌道の元の外部。への最初のアプローチについて
衛星、初期半主軸のより高い値とより低い値のテスト粒子は衛星のヒル半径内に入らず、プロットされていません。


図4：灰色のシルエットの影響または降着角θa
パンの赤道海嶺のトーマスとヘルフェンシュタイン（2020）
北極の上からパンを見下ろしています。 私達も
従来使用されていたplanetocentric West経度をマークします。 内部
シルエットはで観測されたパンの画像N1867602962です。
71◦のリング標高。


図5：潮汐で閉じた月の降着質量の分布。各パネルは、これにより、異なる降着角θaでの降着を示します。
各パネルの左上隅に表示されている角度（度単位）。降着流は、影響を示す赤い線分で示されています
ポイント。各行の右下にある「T」は、降着時に体がタイドロックされたままであると想定されていることを示します。ただしバリエーション
体の形が月をゆっくりと傾けます。月の最初の上面には、緑色の点が付いています。潮汐の向きは
月の最大の主体軸は、垂直方向に沿って整列しています。月の中心は黄色で表示されます。付着物は
オレンジで表示されます。重心はプラス記号で表示されます。軸は、月の初期本体の半長軸を単位としています。
最初は上向きです。これらの降着シミュレーションは2次元で行われました。 a）コアの初期の準長軸と短軸は1.00です
0.99と降着角は負です。パンの赤道の尾根のローブの傾斜は、この兆候と一致しているようです。 b）コアの
初期の準主軸と副軸は1.00と0.95で、降着角は負です。体の向きの角度シフトは、
a）コアの伸びによる。 c）コアの初期の準長軸と短軸は1.00と0.99で、降着角は正です。


図6：度数の関数としての衝撃角または降着角θa
衛星のΔa/ RHからの初期準長軸。 これらは
の衛星の近くの同じ最初の円軌道から計算された
図2に示す円軌道。影響をプロットしました。
丘の単位で、衛星の中心から5つの異なる半径の角度
半径RH。 異なる線は異なる表面半径を表します。 の
衝突角度は表面の半径にわずかに依存するだけです
ただし、テスト粒子の初期軌道の準主軸に強く依存しています。 灰色の点線は式8で与えられます。