マンウェとソロンドールの複雑な回転

マンウェとソロンドールは接触バイナリと言うよりもダンゴ四兄弟的な二重接触バイナリの可能性がある。複雑な光度曲線を満足するには天体４個は必要。以下、機械翻訳。
カイパーベルトの多成分食システム（385446）マンウェとソロンドールの複雑な回転光曲線
（2019年11月19日に提出）
カイパーベルトオブジェクト（385446）マンウェとソロンドールは、2014年から2019年に発生すると予測される相互イベントを持つマルチオブジェクトシステムです。イベントを検出するために、4エポックでシステムを観察しました（UT 2016 8月25および26、2017 7月22日および25、2017年11月9日、2018年10月6）チリ、セロパションの4 m SOARおよび8.1 m Gemini South望遠鏡とローウェル天文台の4.3 m Discovery Channel Telescopeを使用したg、r、VRバンドアリゾナ州ハッピージャック。これらの日付は、4つの下位イベントの不確実性の範囲（+/- 0.5 d）と重なります（ソロンドールがマンウェを掩蔽）。11.88190 +/- 0.00005 hのダブルピーク周期と0.5等の振幅をもつ未解決のシステムの変動性と、長期的な変動性を明確に観察します。マルチコンポーネントモデルを使用して、観測と、ハッブル宇宙望遠鏡を使用してマンウェとソロンドールで別々に測定された以前の測光を同時に適合させます。私たちのフィットは、マンウェが双葉であり、静水圧平衡で密度が約0.8 g / cm3の無力体に期待されるバーベル形状に近いことを示唆しています。
マンウェの場合、最大幅と長さの比〜0.30、直径190 kmの球に相当する表面積、幾何学的アルベド0.06、質量1.4x10^18 kg、および地球の視線から〜75度に向けられたスピン軸を導き出します。ソロンドールの明るさの変化は、〜300-d周期で〜0.6等、システムの長期変動性を説明するかもしれません。予想外に浅い深さと短い継続時間の相互イベントは、近似への残差を説明するかもしれません。このシステムは複雑で、将来のモデリング作業に挑戦的なパズルを提供します。静水圧平衡で0.8 g / cm3。それにより、Manwëの場合、最大幅と長さの比〜0.30、直径190 kmの球に相当する表面積、幾何アルベド0.06、質量1.4x10^18 kg、および地球の視線から〜75度に向けられたスピン軸を導き出します。ソロンドールの明るさの変化は、〜300-d周期で〜0.6等、システムの長期変動性を説明するかもしれません。予想外に浅い深さと短い継続時間の相互イベントは、近似への残差を説明するかもしれません。このシステムは複雑で、将来のモデリング作業に挑戦的なパズルを提供します。静水圧平衡で0.8 g / cm3。

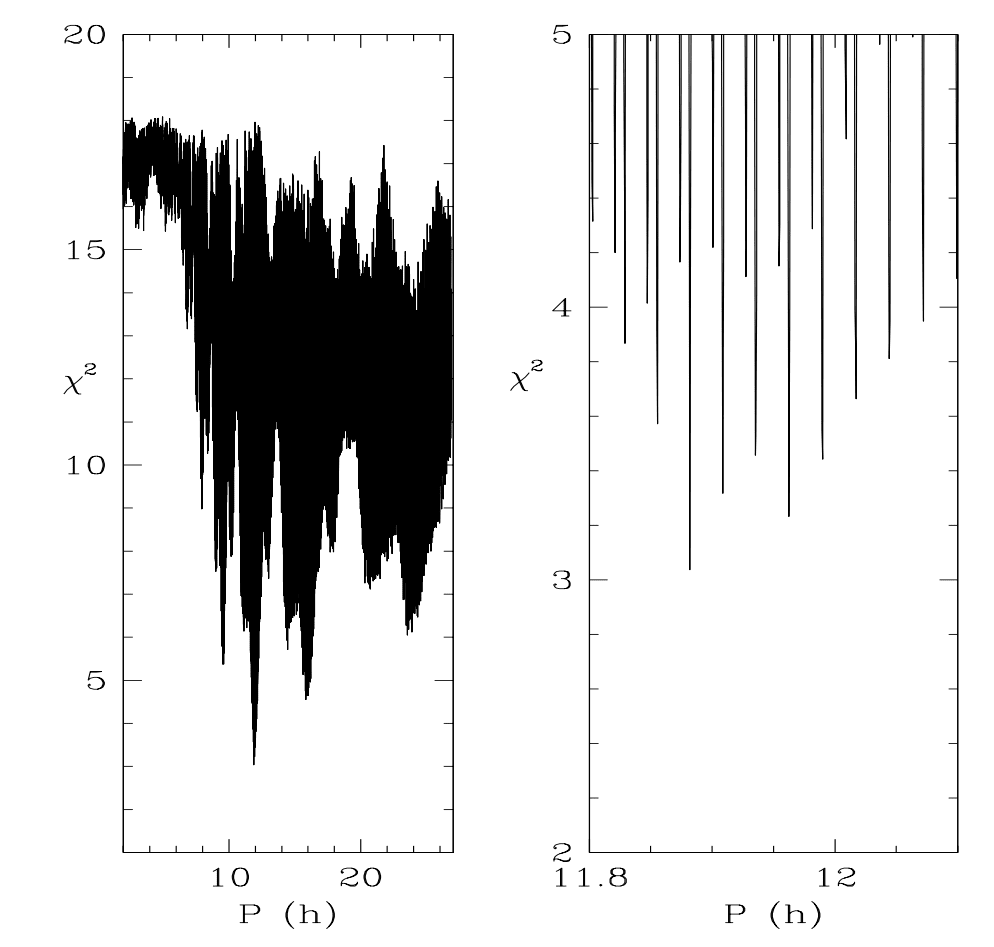
図1.最適なダブルピーク光曲線のc2対周期Pの減少、同時にマンウェ-ソロンドールのSOAR、Gemini、およびDCTの観測、およびマンウェの以前のHSTの観測
ソロンドールからの貢献を含めるための調整後（詳細についてはテキストを参照）。 左側は全範囲を示しています
期間検索の全範囲にわたるc2の削減。 右側は、最小削減c2に近い値を示しています。 見る 最適パラメータの表5。


図2.測定時のマンウェ-ソロンドールの大きさに対する回転位相の減少（上から下）F606WバンドのHST（6つの異なるエポック2007年7月25日から2013年11月20日までに組み立て-
-詳細については、表4のM *およびテキストを参照）、2016年8月25日にgおよびrバンドでSOAR、8月に再び
26、2017年7月22日と2017年7月25日にgとrバンドでジェミニサウス、2017年rバンドでDCT
11月9日、変更前の2008年10月6日のVRバンドのDCT、および変更後の同じDCT VRバンドデータ
変更（詳細についてはテキストを参照）。青、黒、赤、マゼンタの四角はF606W、r、g、VRを表します
それぞれバンド。すべての観測は、太陽への適切な依存関係を取り除くために調整されています
位相角。黒い実線は、最適なダブルハンプド正弦波を示しています（モデルについては表5を参照してください）
パラメーター）。各光曲線は、明確にするために垂直方向に任意にシフトされており、g
g-rの近似値を差し引くことにより、rに対してシフトされた帯域。エラーバーは統計を示します
測定の不確実性に加えて、直交で追加された0.025等の系統的誤差。破線
Manwëを食い隠しているソロンドールから名目上予測される減少を示す（表2を参照）
およびGrundy等。 2014）回転位相への依存は、周期と
表5にリストされている位相パラメータ。緑色は、減少が超える位相範囲を示します。
10％。これらのイベント予測では回転変調はモデル化されておらず、
これらの相互イベントのタイミングは、完全な回転フェーズと同等です。の期間と深さ
また、2つの物体の直径の不確実性を考慮して、イベントは係数2で不確実です。


図3.に示されているマルチコンポーネントライトカーブの計算に使用されるマンウェの形状モデル
この紙。 バーベルモデル（灰色の網掛けの図、長軸、2a、最大垂直線）半径、b）は、正規化された回転を伴う強度のない物体に対してDescamps（2015）によって計算された形状
速度[3p / rG] 1/2 / P = 0.31。 ライトカーブの計算を簡素化するために、この各ローブを表します
それぞれの直径dA = 2bおよびdB = aの一対の接触球（オレンジシェーディング）による図2b。


図4.マンウェ-ソロンドールの振幅と回転位相の減少。これらは同じデータです
図2（凡例を参照）に示されていますが、現在はマンウェがそれぞれが一対の球体として構成された2つの等しいサイズのローブで構成される接触バイナリ（図3を参照）
ソロンドールの回転光曲線は、周期が約300日、振幅が0.55等級です。回転マンウェの周期は、表5にリストされている最適な値と一致します。マンウェのスピン軸の方向
ソロンドールのローテーション期間は、観測に最も適合するように最適化されています（表6を参照）。想定ソロンドールの軌道周期は（測定された不確実性の範囲内で）調整されているため、すべての
相互のイベントは、各夜の観測の時間範囲外で発生します。マンウェには表面積がある直径186 kmの球に相当し、ソロンドールの直径は107 kmです。ランバーシアン散乱モデルはすべての表面に対して想定されています。上の曲線は、HSTで個別に測定されたマンウェ（青）とソロンドール（マゼンタ）の大きさのモデル適合
F606Wバンドで。これらのデータでは、段階的な光度曲線は表示されません。光度曲線の振幅がと形状は、HST観測の長い期間にわたって変化します。また、下の光度曲線は、図2の下から2番目に示されている未調整の第2エポックDCTデータの複製です。