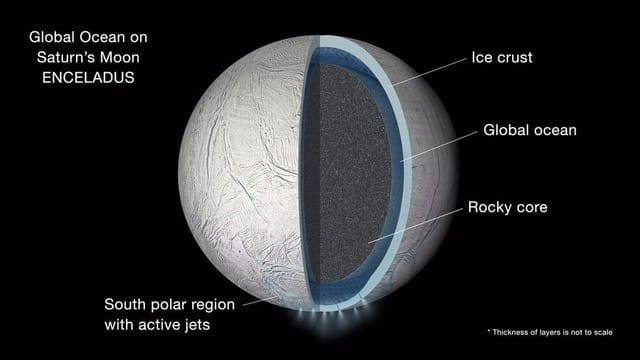
エンケラドスの地下海洋を溶かして噴煙を上げているのに、土星と他の衛星による潮汐加熱で十分なエネルギーが供給される?以下、機械翻訳。
近接衛星と系外惑星の潮の同期化。 3。 再考された潮の消散と エンケラドス への適用。https://arxiv.org/abs/1707.09229
このペーパーがとして1つの体を着ている質量の潮の消散を取り扱うアブストラクトがクリープの潮流理論によって予測されます(Ferraz - メロー、 Cel 。 Mech 。 Dyn 。 Astron 。 116、109、 2013) そして進化方程式をその回転が同時ではありません、しかし同期的な状態の周りに動揺している堅い体に関しては軌道の期間と等しい期間と平均することについての一般的な問題で。 我々は軌道の要素の心の動揺の上に体に、そして従って消散した平均されたエネルギー量に対するこの潮のように誘発された秤動 の影響を論じます。 同期的な堅いボディーの結果として生じている消散はそれのアンドラーデモデルを思い出させるが、別のマックスウェル法からの逸脱を見せます。 結果は エンケラドスの回転に応用されます、そして観察された消散(γ = 6×10 - 8つのs - 1)を説明するために必要なリラックス要因は惑星の衛星のために予想される規模を持っています。 若干のミスの訂正とペーパー II (Ferraz - メロー、 Cel 。のタイプミス Mech 。 Dyn 。 Astron 。 122、359、 2015) ペーパーの終わりに含まれます。
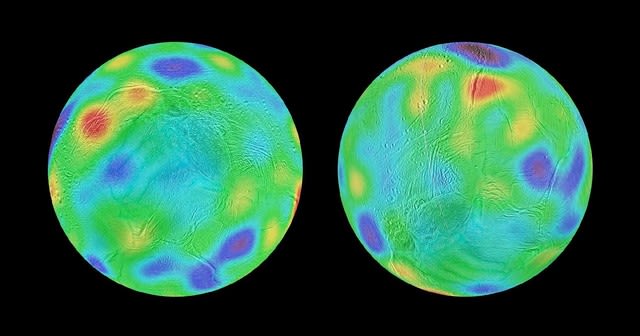
近接衛星と系外惑星の潮の同期化。 3。 再考された潮の消散と エンケラドス への適用。https://arxiv.org/abs/1707.09229
このペーパーがとして1つの体を着ている質量の潮の消散を取り扱うアブストラクトがクリープの潮流理論によって予測されます(Ferraz - メロー、 Cel 。 Mech 。 Dyn 。 Astron 。 116、109、 2013) そして進化方程式をその回転が同時ではありません、しかし同期的な状態の周りに動揺している堅い体に関しては軌道の期間と等しい期間と平均することについての一般的な問題で。 我々は軌道の要素の心の動揺の上に体に、そして従って消散した平均されたエネルギー量に対するこの潮のように誘発された秤動 の影響を論じます。 同期的な堅いボディーの結果として生じている消散はそれのアンドラーデモデルを思い出させるが、別のマックスウェル法からの逸脱を見せます。 結果は エンケラドスの回転に応用されます、そして観察された消散(γ = 6×10 - 8つのs - 1)を説明するために必要なリラックス要因は惑星の衛星のために予想される規模を持っています。 若干のミスの訂正とペーパー II (Ferraz - メロー、 Cel 。のタイプミス Mech 。 Dyn 。 Astron 。 122、359、 2015) ペーパーの終わりに含まれます。





















※コメント投稿者のブログIDはブログ作成者のみに通知されます