www.DeepL.com/Translator(無料版)で翻訳しました。
惑星形成ディスクにおける光蒸発のモデル化
概要
若い星を取り巻くガスとダストの円盤から惑星が誕生する。
惑星は、若い星を取り囲むガスやダストの円盤から生まれる。中心星からの高エネルギー放射は、円盤の大気から熱流出を引き起こし
円盤の大気から熱流出し、円盤や惑星系の進化に大きな影響を与える。
円盤と惑星系の進化に強い影響を与える。このような背景から、様々な複雑さを持つ数値モデルが開発され
このような背景から、中心星から円盤が光蒸発する過程を研究するために、様々な複雑さを持つ数値モデルが開発されている。
我々は、数値計算の手法、結果、そして現在のモデルの予測性
また、これらのモデルを制約するための観測的なテストについて述べる。
1 はじめに
惑星系の形成と進化は、惑星系を構成する天体の進化と最終的な散逸と強く結びついている。
惑星系の形成と進化は、それらが形成される原始惑星系円盤の進化と最終的な散逸と強く結びついている。
これは、中心星からの照射によって、加熱、電離(したがって磁気的な変化)、そして
加熱、イオン化(つまり磁場との結合)、そして原始惑星系を分散させる熱流の引き金となる
熱流出が起こり、円盤の物質が拡散する。
ガス円盤の拡散は、巨大惑星が形成されるまでの最終的なタイムスケールを決定するものであり
巨大惑星が形成される最終的なタイムスケールを与え、惑星系の最終的な構造にとって非常に重要である。
惑星系の最終的な構造にとって極めて重要です。光蒸発の仕組みは、まず円盤に隙間を開け
2 惑星形成円盤における光蒸発のモデル化 これは、移動する惑星に自然な駐車メカニズムを提供し[1-4]、また円盤後の軌道の力学的進化に影響を与える[5
軌道の進化に影響を与える[5, 6]。巨大惑星集団の最終的な半長軸分布は
巨大惑星集団の半長軸分布は、円盤の質量放出プロファイルに極めて敏感である [2, 3] 。
に非常に敏感である [2,3]。
惑星形成の初期段階における光蒸発の役割、例えば
惑星形成の初期段階、例えばストリーミング不安定性による準惑星の形成における光蒸発の役割については、代わりに議論されている
[7, 8]. ストリーミング不安定性が起こるためには、ガスに対する固体の割合が高いことが必要である。
必要である.光蒸発は、ガスを優先的に除去し、局所的にダスト/ガス比を増加させるメカニズムとして、通常、引き合いに出される。しかし
[7] はこの仮説を検証し、光蒸発が惑星全体の質量に与える影響はほとんどないことを明らかにしました。
7] がこの仮説を検証し、惑星の総質量に対する光蒸発の影響は無視できるとしたのに対し、逆の結論が
[8]では逆の結果が得られています。この不一致の理由は、光蒸発による質量減少のプロファイルの違いにあります。
光蒸発の質量損失プロファイルの違いにある。
現実的な質量損失分布は、惑星や円盤の人口合成モデル[e.
また、惑星や円盤の人口合成モデル[9-11]では、熱力学的な密度分布と一致する円盤表面の
熱力学的な風構造と矛盾しない円盤表面密度分布は、遷移円盤の観測結果を解釈する上で
遷移円盤の観測[12-15]やガス輝線・塵の観測[16-20]の解釈にも重要である。
線とダストの観測[16-20]を解釈する上で極めて重要です。
このような背景から、惑星形成円盤における光蒸発過程の理論的・数値的モデルが長年に渡って開発されてきました。
その主な目的は、空間分解された正確な質量放出率
質量損失率を正確に求めることを主目的としている。
最近の理論的・観測的な進歩 [レビュー 21, 22] によれば
最近の理論や観測の進歩により、熱風(光蒸発風)に加えて磁気風(MHD風)を指摘する
最近の理論・観測の進歩により、熱風(光蒸発風)に加えて磁気風(MHD風)の存在が指摘され、熱風の定量的予測モデルの開発が急務となっています。
観測で区別するために、定量的に予測可能な熱風モデルを開発する必要性を高めています。
を区別するために、定量的に予測できる熱風モデルの開発が急務となっています[18, 23]。このことは
MHD風とディスクからの角運動量抽出の関連性を評価するために最も重要である。
この論文では、数値光蒸発モデルの現在の地位をレビューする。この論文では、光蒸発の数値モデルの現状をレビューする。
特に、異なるモデルの適用性、および、結果の分岐に注目する。現在および将来の
観測によるモデルの検証についても述べる。
2 数値モデリング
円盤光蒸発は、放射伝達、熱化学、流体力学、ダストダイナミクスの連成問題である。最近まで、これらの効果を
しかし、近年、そのコードと数値計算能力が明らかになりつつあります[24,25]。
24, 25] が利用可能であることが示されています。
放射伝導 理論的な光蒸発モデルは、次の3つのうちの1つ、またはその組み合わせに対して開発されてきました。
理論的な光蒸発モデルは、恒星スペクトルの3つの異なる部分の1つまたは組み合わせに対して開発されました。
遠紫外線(FUV)6eV < hν < 13.6eV、極紫外線(EUV)6eV。
極端紫外線(EUV), 13.6eV < hν < 100eV; およびX線, 100eV < hν < 10keV
(特に軟X線は100eV < hν < 1keV)。それぞれ
の特徴や数値的な課題があり、これらを区別することが重要である。
区別することが重要です。
EUV放射
EUV光は、原子状水素を電離するのに十分なエネルギーを持つ光と定義され
を電離するのに十分なエネルギーと定義されている(hν > 13.6 eV)。中性水素の電離断面積は10^-17cm^2atomなので
中性水素の電離断面積は10^-17cm^2atom^-1であるため
であるため、EUV光子は、中性水素のカラム密度
中性水素の柱密度 NH = 10^17 cm^-2 を通過すると吸収される。
. EUV光と水素原子の相互作用は単純である。
光子と水素原子の相互作用は単純である。光子は吸収され、電離した水素原子が生成され、熱エネルギーが発生する。電離した領域での典型的な温度
電子-イオン対の生成は、再結合により相殺される。電子が基底状態になると、13.6e以上のエネルギーを持つ光子
が生成され、これがさらに媒質をイオン化し、拡散磁場を生成する。一方、励起状態への再結合は、電離光子の破壊につながる。
イオン化した光子は破壊される。の中心星から照射された場合。
の中心星から照射された場合、中心星からの光子は内部円盤の上に約10^4Kの高温静水圧大気を発生させる。このとき
この大気からの再結合光子の拡散場が、外層円盤を照射し
外側の円盤を電離させる。この問題は、2次元の輻射伝導として解かなければならない。
この問題は、直接電離場と拡散電離場を考慮した2次元放射伝達として解く必要があり、光電離問題を解くと同時に
この問題は、光電離の問題を解決しながら、直接電離場と拡散電離場を考慮した2次元放射伝達として解く必要がある。
FUV放射
FUV光子は、6~13.6eVのエネルギーを持ち、水素を電離することはできません。
水素をイオン化することはできませんが、水素分子、CO
などを光分解し、炭素を電離する。塵埃からの光電加熱
と多環芳香族炭化水素(PAHs)からの光電加熱が、FUV光子の主なガス加熱メカニズムである。
による光電加熱が主流である。加熱は粒子表面に比例する。
したがって、円盤大気中に小さな粒やPAHsが豊富に存在する場合、FUVはガスを加熱する。
FUVはガスを加熱し、熱風の駆動に寄与する可能性がある
[26]. ガスが放射するエネルギーは、ダストが処理するエネルギーの1%未満に過ぎません。
ガスが放射するエネルギーは、ダストが処理するエネルギーの1%以下であり、主に小さなダスト粒やPAHからの光電子によって衝突的に加熱される
やPAHsからの光電子、あるいは振動励起したH2によって主に衝突加熱されます。そのため、その温度は
ダストの進化と化学の両方から影響を受けます [24, 27]。FUV光子は、主にHとH2の中性層を
中性HとH2の層を10 -5000 Kの温度まで加熱することができます。
フラックスの大きさ、ガスの密度、化学的性質に依存します。
この問題を正しくモデル化するためには、2次元の放射伝導と、密度や温度の激しい変化を考慮した十分に大きな化学ネットワーク、そして適切なダスト進化モデルを組み合わせる必要があります。もう一つの複雑な問題は
は、降着による恒星のFUV磁場成分が
が色球成分よりも大きいという事実があります。これは
ということは、円盤に到達するFUVフラックス、ひいては風の質量損失率は
降着率に強く依存し、降着率は時間とともに減少し、内部空洞が形成されると完全に停止します。
この降着速度は時間とともに減少し、内腔が形成されると完全に停止する。
X線放射
X線は大きく分けて、軟X線(100 eV < hν < 1 keV)で吸収され、円盤上層を加熱して熱風を起こすものと、硬X線に分けられる。
で吸収され、円盤上層を加熱して熱風を起こす軟X線と、硬X線
(1 keV < hν < 10 keV) は、円盤のずっと深いところまで到達し、塵とガスが熱的に結合する。
硬X線(1keV < hν < 10keV)は、塵とガスが熱的に結合している円盤のずっと奥まで届くが、電離度を高めることができる。
(硬X線(1 keV < hν < 10 keV)は、ダストとガスが熱的に結合している円盤の深部にまで到達するが、円盤中間面付近では(宇宙線と一緒に)電離度を高め、ガスと円盤磁場との結合に影響を与える。X線
X線光子の主な相互作用は、原子や分子の内殻の光電離である。
水素を含む)二次的な電離を引き起こし、次に一次電子と二次電子の運動エネルギーによる熱化。
X線加熱は、高密度のX線PDRでは数百K、低密度のX線PDRでは数十Kの温度域を生じます。
X線加熱は、高密度のX線PDRでは数百Kから、円盤上層では10^4Kの温度範囲を生じます。X線ルミノシティー
は星降着率に依存せず、最初の数年間はほぼ一定であり [28]、風による質量放出率が一定であることがわかる。
X線輝度は恒星降着率に依存せず、最初のMyrsでは時間に対してほぼ一定であり [28]、ディスクの表面密度の変化に関係なく、一定の風速の質量損失率が得られる。
2.1 方法
円盤光蒸発の重要性が認識された30年以上前 [29] から
30年以上前 [29]、この問題は、放射伝達モデル、あるいは
輻射伝導モデリングや時間依存の輻射流体力学に重点を置いてこの問題に取り組んできた.
ディスク光蒸発の最初の研究は、強いEUV放射体であるOB星によるディスクのEUV光蒸発に焦点を当てたものであった。2つのモデルライン
が同時期に開始された。一つは、エディントン近似による簡略化された放射伝達計算を採用したもの(3次元の放射伝達問題を
三次元の放射伝達問題を、恒星から鉛直上方に来る「3本の流れ」近似にする。
円盤の各点で鉛直上方、下方から来る "3つの流れ "に近似する)を採用したものである。
を、鉛直静水圧円盤に適用した [30, 31]。2つ目は、より力学に焦点を当てたもので
2次元流体力学光電離コードを開発することから始まりました。
コードを開発することから始まり、後に紫外線による塵の散乱の効果を含めて改良されました [34]。どちらの研究でも
どちらの研究でも、風に対する最も重要な寄与は
からの拡散場であること、そして熱風が重力半径は重力半径Rg1の外側にあることがわかった。EUVによる質量損失率を円盤半径の関数として解析的に定式化したものを加えることにより
光蒸発による質量損失率を、1次元の円盤粘性発展方程式のシンク項として解析的に定式化し
[37, 38]に追加することで、いわゆる「EUVスイッチ」が実証された(セクション3参照)。
最初のEUV光蒸発の流体力学的モデルは、T Tauri星
39]は、等温状態方程式を仮定し、流れの底の密度を以前の結果[31]から仮定して行われました。その結果、光蒸発流は重力半径よりもずっと小さな半径から亜音速(約0.3 cs)で打ち上げられることがわかった。
重力半径(Rc ' Rg/5)よりもはるかに小さな半径から亜音速(∼0.3 cs)で立ち上がることを発見した [36も参照のこと]。
これは解析的処方からは予想されないものであった。
これらの研究に続いて、T-TauriからのX線照射の最初の静水圧モデル
最初は単純な加熱モデル [40]、後に、より現実的な2次元モンテカルロ計算による
より現実的な2次元モンテカルロ光電離・ダスト放射伝達コード [41, 42
放射伝達コード [41, 42] を用いて行いました。後者の計算では、より現実的な
EUVとX線の両成分を含むより現実的な入力スペクトルを用いた計算を行った結果
後者の計算では、後者が完全に支配的であり、質量損失率が2桁ほど高くなることが示されました。
X線が支配的であることを示した。
同時に、EUV、X線、FUVを含む1+1次元静水圧平衡モデル、および包括的な化学ネットワークも開発された
[26, 43]. これらのモデルは、FUV放射がディスク外側の物質を除去するのに有効かもしれないが、それはディスクにPAHが豊富にある場合のみであることを示した。しかし
しかし、これらのモデルで使われた入力スペクトルは非常に理想的であり、硬X線の入力スペクトルは効率が悪い。
硬X線の入力スペクトルであり、ガスを加熱し、風を駆動するのには非効率的であった。
風を起こすには不十分でした。
これらのモデルは、適切な流体力学的計算をすることなく、すべて
という仮定で局所的な質量損失率を推定していました。
と仮定して局所的な質量損失を推定した。
いわゆるρc˙s法である。流体力学を用いない場合、風の基部を特定するのはかなり恣意的であり
流体力学がなければ、風の根元の特定はかなり恣意的であり、著者によって異なるアプローチをとっていたため、両者の緊張はさらに高まった。
このことが、モデル間の緊張をさらに高めることになった。X線とEUVの両方を含む最初の(放射線)流体力学計算[44, 45]は、詳細な熱処理から得られたイオン化パラメータを関数としてガス温度をパラメータ化することで行われました。
EUV放射[44, 45]を含む最初の(放射線)流体力学計算は、mocassinコードで行った詳細な熱・イオン化計算[42]から得たイオン化パラメータの関数としてガス温度のパラメータ化を用いて行った。
mocassinコード[46-48]を用いて行った詳細な熱・電離計算[42]から得られた電離パラメータの関数としてガス温度をパラメータ化して行った。
イオン化パラメータは、ξ = LX / nr2 、ここでLXはX線光度、rとnは局所的な円盤の半径とガスの体積密度を表します。この
この方法は、一般に ξ - Te 法として知られている。これらの研究は、後に
現代の流体力学コードpluto [49]を用いて拡張され、円盤の減衰効果をよりよく考慮するようになりました。
柱密度に依存するξ - Teパラメタリゼーションを用いて円盤の減衰効果をよりよく考慮した[50-53]。この改良された処方箋により
X線照射が数百auに達する可能性があること、また、高輝度X線の質量損失率が
高輝度X線の質量損失率は、より高エネルギーな光子が低輝度X線を加熱できないため、プラトーに到達する。
X線照射は数百auに達し、高エネルギー光子が円盤の低密度の冷たい領域を加熱できないため、高X線光度での質量損失率はプラトーに達することが示された。
ξ - Te 法の利点は、詳細な多周波熱計算に基づいていながら
多周波熱計算をベースとしながらも、流体力学の計算オーバーヘッドをほとんど発生させないことです。
この方法の利点は、詳細な多周波熱計算に基づいているにもかかわらず、流体力学の計算オーバーヘッドをほとんど発生させないことです。この手法の欠点は
熱計算が放射平衡で行われるため、断熱冷却の寄与が考慮されないことである。ξ -Te 法で行ったすべてのモデル
したがって、ξ -Te 法を用いたすべてのモデルは、放射平衡が正当であることを保証するために、事後チェックを行う必要があります。
を行い、シミュレーション領域全体で放射平衡が成立していることを確認する必要がある。これは
このことは、この手法で得られた全てのモデルで実際に実証されている
これまでのところ[44, 50-53]である。
最近、いくつかの数値実験が行われ、(非常に合理的な)放射伝達と
非常に合理的な)放射伝達と熱化学計算をオンザフライで行う数値実験が行われました。
を流体力学モデルで実行する数値実験が行われている[24, 25]。このアプローチは計算コストが高いため
このアプローチは計算コストが高いため、限られたスペクトルや空間分解能のモデルしか存在しません。
のみである.これらのモデルで得られた結果は、ξ - Te法で得られた結果と強く乖離しています。
これらのモデルで得られた結果は、3.1節で議論したように、ξ - Te 法で得られた結果と強く乖離している。
3 結果
これまでに開発されたすべての光蒸発モデルの主な結果は以下の通りである。
中心星からの放射が原始惑星系円盤の上層を加熱する。
原始惑星系円盤の上層部は、中心星からの放射によって加熱され、熱流として遠心力により加速され、原始惑星系円盤は拘束を解かれ
熱流で遠心加速される。風の質量放出率は、原始惑星系円盤の特定の
重力半径と呼ばれる円盤の特定の半径付近でピークを示し、そのプロファイルは多かれ少なかれ大きな半径に
を持つ。星に近い領域では質量放出が起こらないことが予想される
星に近い領域、つまり重力的に拘束されている領域からは質量放出が起きないと考えられる。
そのため、ガスを逃がすには非常に高い温度が必要となる。そのため
光蒸発による定常的な質量放出と、時間とともに定常的に減少する降着率の組み合わせが
光蒸発による定常的な質量損失と、粘性降着円盤における定常的な降着率の減少の組み合わせにより、いわゆる
光蒸発スイッチと呼ばれるものです。円盤が粘性的に進化するのは、数百万年前までである。
円盤は数百万年、あるいは粘性降着速度が風の質量損失率と同程度になるまで粘性進化する。
粘性降着速度が風の質量損失速度に匹敵する値に達するまで、円盤は数百万年間粘性的に進化し、その時点で光蒸発が起こり、円盤は内側から急速に分散する。
光蒸発が起こり、円盤は内側から外側へ急速に拡散していく。
空洞が形成される。
現代の光蒸発の流体力学的モデルは、(少なくとも)
しかし、惑星を含む3次元シミュレーションについては54を参照のこと]。
のみで行われ、その間に流出の定常解が得られる(理想的には)。円盤の表面密度の進化をモデル化すると
円盤の表面密度の変化をモデル化することは
一般に2次元流体力学的な計算では実現不可能です。そこで
は、2次元定常解を用いて、一次元質量損失プロファイルΣ˙ w(R) [37, 38, 55, 56]を決定し、これを一次元のシンク項として
を1次元の円板粘性発展方程式 [57, 58] にシンク項として加える。
にシンク項として導入し、時間の関数として円盤の表面密度進化を調べる。
∂Σ/∂t = 1/R ∂/∂R (3R^1/2 ∂/∂R(νΣR^1/2)) - Σ˙ w(R, t). (1)
図1、1Mの質量放出プロファイル(右図[52])と、それに対応する表面密度の変化(左図)を示す。
表面密度の変化(左図)を示す。表面密度進化(ギャップが開く時間と場所、拡散のタイムスケールなど)は、Σ(˙ R)
Σ(˙ R)に非常に敏感であり、このことは円盤内で形成される惑星の最終的な構造にも影響を与え [1-3]、また光蒸発による
ストリーミング不安定性による準惑星形成の引き金となる可能性もある [7, 8]。
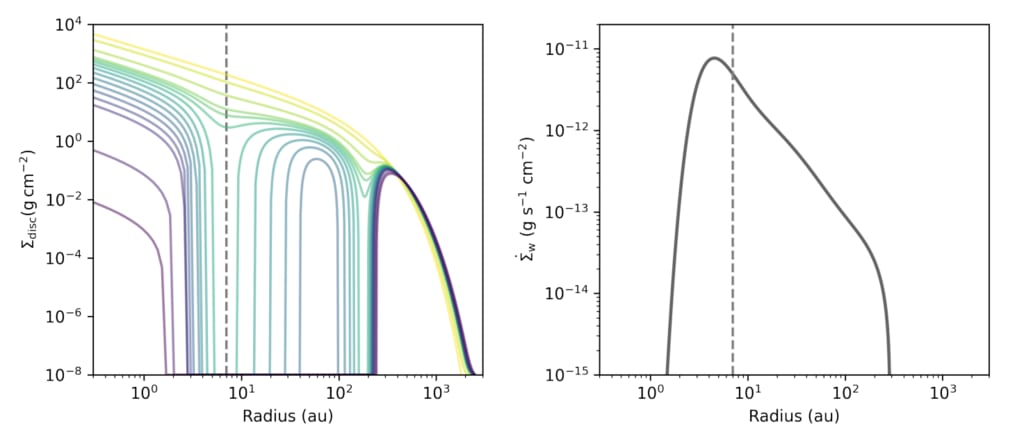
図1 左図は、太陽質量の恒星の周りを回るMd=0.1Mの円盤について、円盤半径の関数としての1次元表面密度進化を示したもの。
太陽質量の星を周回するMd=0.1Mの円盤の場合。
[52]. 異なる線は[0, 25, 50, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 90, 99]の位置に描かれている。
%で描かれている。点線は、光による内部ギャップ開口部のおおよその位置
点線は光蒸発による内部ギャップの開口部のおおよその位置を示す。右図では、対応する
光蒸発による表面密度質量損失率を円板半径の関数として示している。
3.1 結果の乖離
上記のような大まかな図式はほとんどの著者によって共有されているが、各プロジェクトで導出された
Σ˙ w(R)と、異なるプロジェクトで得られた風の物理的性質
(例: 表 1 参照) は大きく異なっている。最近行われた、異なるモデル間の表面
密度質量損失について、円盤光蒸発の異なるモデル間の比較 [22,
図7参照]は、円盤光蒸発の異なるモデル間における表面密度質量損失の桁違いを明らかにした。
累積質量損失率に一桁の差があることが明らかになった。
これは、表面質量損失率の最大値の位置だけでなく、プロファイルの範囲にも依存する。これらの
これらの違いは、恒星の照射に採用した周波数帯の
この違いは、恒星照射に用いた周波数帯の選択と、使用した手法の違いによって大まかに理解できる。
を用いた。しかし、ほとんどの場合、10Åの範囲にピークがあり、表面密度質量損失率は緩やかに減少し
しかし、その多くは10au付近にピークを持ち、外側の領域では表面密度質量損失率が緩やかに減少している。
光蒸発は恒星からの照射によって起こるので、このような
光蒸発は恒星の照射によって駆動されるため、乖離の大部分は、異なる著者によって仮定された入力スペクトルを考慮することによって理解することができる。
の議論も参照)。純粋なEUVモデル
[e.g. 60, 61] は、10^4 K付近の温度でほぼ等温のガスを生成する。
この場合、質量放出は重力半径付近でピークに達し、1Mの星では約
この場合、質量放出は重力半径付近でピークを示し、その値は1Mの星で約9au、全質量放出はEUVの平方根としてスケールし
の平方根に比例し、10^41 phot/secのEUVフラックスと仮定すると、およそ10-10 M/yrとなる。
[60, 61].
軟X線は、EUVよりもディスクの深い部分を透過するため
軟X線はEUVよりも深く透過し、古典的なEUVモデルよりも1〜2桁高い質量損失率が得られる。
軟X線は、EUV放射よりも深く円盤を透過し、古典的なEUVモデルよりも1〜2桁高い質量損失率をもたらす。
のX線輝度にほぼ線形に依存し、古典的なEUVモデルよりも1〜2桁高い質量放出率を得ることができる [45, 50, 52]。X線光蒸発モデルには、すべて
X線光蒸発モデルは、EUV成分を含むが、風の駆動には無関係であることを発見した [42など]。1M星のモデルでは、ソフトスペクトルと1030erg/secのX線ルミノシティを仮定すると、10-8M/yrの質量放出速度が得られた [44, 50]。X線による質量損失のプロファイルは、EUVの場合よりもはるかに拡張され、重力半径付近でピークとなる
重力半径付近をピークに、約200auまで広がっている。炭素は
X線は主に炭素の内殻に吸収されるため、X線不透過の主要な要因の一つである。
X線は主にガスやダストに含まれる重元素の内殻に吸収されるため、炭素はX線不透過の主要な要因の一つです。
の内殻に吸収されるからです[62]。炭素の枯渇は、円盤の進化に伴う自然な結果として予想されます。
炭素の減少は、炭素がCOからより複雑な種に変化する化学的進化と、炭素の大部分を氷の中に閉じ込める粒成長による物理的進化の両方から、円盤進化の自然な結果として予想される。
炭素の枯渇は、円盤の進化に伴う自然現象であると考えられる。炭素が枯渇した円盤では、その質量損失の大きさと範囲は
質量損失率の大きさと範囲は、炭素が枯渇した円盤では、ファクター∼2倍に増加すると予想される [51]。内部
FUV放射が円盤のさらに外側から光蒸発を引き起こすと予想される。
26]の静水圧平衡モデルに基づいた初期見積もりでは
の静水圧平衡モデルに基づく初期見積もりでは、多環芳香族炭化水素(PAH)の光蒸発が非常に効率的であることがわかった。
多環芳香族炭化水素(PAHs)が円盤の大気中に豊富に存在するとの仮定で、非常に効率的であることがわかった。しかし
T-Tauriディスクではほとんど観測されないPAHsの大気中存在量
[63]ではほとんど観測されず、さらに恒星のFUVフラックスは中心星への降着率に依存するため、大気中のPAHsは非常に小さいと考えられる。
に依存し、時間とともに減少する。これらの理由から
は、最終的な円盤の拡散にどのような役割を果たすかは不明である。
より最近の計算 [25] では、EUV、FUV、X線
を同時に考慮した最近の計算 [25]では、直接のEUVフラックスが風の駆動を支配しているという結論に達しています。
しかし、その結果、EUVだけを使ったモデルよりも2桁も高い質量放出率という結論に達しました。
これらの計算は恒星からの直接のEUV光は、円盤の内側で吸収され
を吸収し、膨張した円盤の内側から来る拡散磁場が光蒸発を促進するという古典的な描像とは対照的です。
光蒸発は重力半径の範囲内で(低速で)行われる。
EUVが直接届くと仮定した場合、重力半径を超えたところでも光蒸発が起こる。
重力半径以上ではEUVの直接照射が可能であるという仮定は、過去の計算に基づくものである[64]。この計算と過去の計算との間の矛盾の原因は、次のような点にあると考えられる。
この計算では、円盤の内側が外側の領域を遮蔽するほど膨張していない。
ディスクの内側が外側の領域を遮蔽するほど膨張しない場合や、大きなフレアリングがある場合など。
は、ほとんどのディスクに当てはまらないかもしれない[65]。最後に、これらの結果は
は、詳細な2次元モンテカルロRTと熱計算を行った先行研究[42]とも矛盾しない。
モンテカルロRTと静水圧円盤の熱計算によって、EUVの役割を明確に検証している[42]。
観測的に得られたX線スペクトルの存在下でEUVの役割を明示的に検証し、最終的な質量損失率にEUVの効果が無視できることを見出した。A
しかし、最終的にこの矛盾の原因を明らかにするためには、専門家による詳細な比較を行う必要があります。
この不一致の本質を明らかにする必要がある。
また、最近の計算[24]で得られた風の物理的性質
最近の計算 [24] では、Athena++コード [66, 67] を用いて自己無撞着な輻射流体計算を行い
を用いた自己無撞着な輻射流体力学と光電離円盤の熱化学計算による計算 [24] と、ξ -Te アプローチを用いた計算 [44, 45, 50, 52] との間に強い乖離がある。
また, 風の物理的性質についても強い発散が見られる.
最近の計算 [24] では、Athena++コード [66, 67] を用いて自己無撞着な輻射流体計算と光電離円盤の熱化学計算を行った結果、ξ -Te 法を用いたモデルと比較して
を用いた自己無撞着な輻射流体力学計算や光電離円盤の熱化学計算を行ったモデル [24] と、ξ -Te アプローチを用いたモデル
[44, 45, 50, 52, 53]. 得られた全質量損失率は同程度であったが
Athena++モデルは、X線放射は風の駆動に非効率的であるという結論に達し
であり、EUVが支配的であるという結論を得た。また、風の温度構造も
の温度構造も両者で大きく異なる。Athena++モデルでは、風の根元で非常に高い温度(10^5K)が予測され、上空に行くほど温度が下がる
Athena++では風の根元が10^5Kと非常に高く、上へ行くほど低くなる。
ξ - Teモデルで得られたパーカー的な風とは対照的である。
10^4Kに達するが、それは風のごく限られた領域だけである。
しかし、それはEUV放射によって加熱される(発射されない!)風の非常に限られた領域だけである。これらのモデルの乖離は
これらのモデルの相違は、しばしば、放射伝達と熱平衡へのアプローチ方法に関する方法論の違いに起因するとされてきました。
放射伝達と熱平衡へのアプローチの仕方、採用する照射スペクトル
を選択し、ガスを冷却するために利用可能なプロセスの違いに起因している。最近の詳細な比較 [68] によって、この問題に光が当てられ、以下のことが示された。
これらのモデル間の乖離は、主に照射スペクトルの選択によるものであり
照射スペクトルの選択と、非常に限られた数の周波数点によって引き起こされていることを明らかにした。
と比較して、Athena++モデル(7)では、放射場を記述するために使用される周波数点の数が非常に限られている。
ξ -Te モデル (>1000) と比較して、Athena++ モデル (7) では照射スペクトルの選択と放射場を記述するための非常に限られた数の周波数ポイントに起因する。ξ -Te モデルでは、T-Te のチャンドラ観測から得られた X 線スペクトルを用いています。
Chandra による T-Tauri 星の深い観測 [41, 53, 69] から得られた X 線スペクトルを用いているのに対し、Athena++ モデルは解析的な分布を仮定している。
モデルは解析的な分布を仮定している。
4 観測的検証
複雑な理論モデルが数値実験に留まることなく、自然現象の現実的な記述になるために
数値実験にとどまらず、自然現象の現実的な記述となるためには、複雑な理論モデルが
観測結果に対して検証可能な予測値を提供することが非常に重要である。この
この節では, 理論的な光蒸発モデルを制約するために用いられてきた直接的, 間接的なテストを列挙する.
光蒸発理論モデルを制約するために使用された多くの直接的および間接的なテストを列挙する.
4.1 直接的テスト
風は細く、そのガス成分を直接撮影することは不可能です。
しかし、風の気体成分を直接「観測」することは可能である
アウトフローで放出され、青くシフトした成分を示す輝線の高分解能分光法 [21, 22]によって、風のガス成分を直接「観測」することができます。衝突電離線
中性・低電離種([OI]、[NeII]、[SII]、[N2]、[FeII])の衝突イオン化線のプロファイル。
[FeII])、およびいくつかの分子トレーサー(COとH2)は、統計的に有意な数のT-Tauri星について利用可能です[e.g. 70-72]。観測されたプロファイルの大部分は
観測されたプロファイルの大部分は、X線駆動型光蒸発モデル
(16,17,73)であり,複合プロファイルを示す天体では,磁気駆動成分と組み合わせて
(図2参照)。サブミリ波領域の線(例.
COやCI)もまた、高傾斜天体の円盤風の存在を推測するのに使われてきた [74]。
また、数値MHD風モデルによる予測も存在します[75]。
による予測も存在する[75]。
風と円盤の大気領域における電離ガスも、自由電子を介することで
のような高空間分解能の観測装置を用いて、波長数cmの自由放射で検出し、空間的に拘束することができる。
ngVLA のような高空間分解能の観測装置による観測 [例
23]. これは、星に近い領域から吹いている磁気風を区別するための有望な方法である。
これは、光蒸発風よりもはるかに星に近い領域から駆動される磁気風を区別するための有望な方法です。
小さな(10μm以下の)塵粒は、打ち上げ領域からの風に巻き込まれる可能性があり [76-83]、高傾斜天体の散乱光観測、特に内部にダストキャビティを持つディスクから、そのサインを検出できる可能性がある [19-20]。
の散乱光観測で検出できるかもしれない[19, 20]。
4.2 間接的な検証
光蒸発モデルが一致すべき間接的な制約には、次のようなものがあります。
(i) 降着特性と表面密度の進化によって追跡可能な円盤の分散タイムスケールの観測結果。
観測された円盤集団の降着特性や表面密度の進化によって追跡できる。
を含む、観測された円盤集団の降着特性と表面密度の進化によって追跡できる、円盤分散の時間スケール [例えば 77, 84-89]; (ii) メタリシティ依存性
ディスク寿命の金属量依存性 [25, 62, 90-93]; (iii) 観測されたディスク集団の相関関係(M˙ - M?
M˙ - M?関係のような円盤個体群における観測相関[例えば94-96]。
ここで重要なのは、光蒸発モデルを検証するために、観測された円盤の個体数に対して風の性質
光蒸発モデルを観測された円盤集団に対して検証するためには、風の性質(円盤半径の関数としての質量損失率)を十分に広いパラメータ空間に対して計算する必要があることに注意する必要があります。
観測された恒星質量とX線の性質にまたがる十分広いパラメータ空間について計算する必要があることに注意してください。その際
その際、角運動量がどのように輸送されるかを仮定する必要がある。これまでのほとんどの
これまでの研究では、光蒸発と組み合わせた粘性モデルを仮定しています。このような研究を繰り返すことは興味深いことです。
磁化された円盤風による角運動量輸送を仮定したこの一連の研究は興味深いものです。
5 展望
前節の最後に述べたように、磁気化した円盤風は熱風と組み合わせて存在する可能性がある。
が熱風と混在して存在し、粘性に代わって角運動量輸送の支配的な機構を提供するかもしれない。
粘性の代わりに角運動量輸送の支配的な機構となるかもしれない。その存在を直接示すヒントが、いくつかの天体で観測された輝線プロファイルに見られます。
を観測したところ、複数の流出成分を示す天体があることがわかった [例えば、22,最近のレビュー]。さらに、非理想的な磁気流体力学モデルである
は日常的に磁化された風を観測していますが、磁気回転不安定性をディスクのほとんどの領域で維持するのに苦労しています[e.g. 59, for a recent review]。
レビュー]。明らかに、円盤風のモデリングのフロンティアは、この2つのプロセスを同時に、かつ十分な空間分解能で説明することであり、その結果、以下のようなモデルを作り出すことができる。
ということです。
最初の試みは有望である[e.g. 99, 100]が、それらはまだ、円盤の内側領域(観測されたほとんどの領域)における解像度が不十分である。
の解像度が不足しており,また,(ほとんどの観測結果が得られる)円盤内領域では
また,放射伝達を単純化しすぎたり,制約のない多くのパラメータに頼っているため
磁束とその変化を記述するために多くの制約のないパラメータに依存している。
その進化を記述するための多くの無制約なパラメータに依存している。これらの問題を克服することができれば、これらのモデルは
観測結果との比較に十分な予測力を得ることができる。
その結果、原始惑星系円盤の進化を理解するための強力なツール
原始惑星系円盤がどのように進化し、最終的にどのように散逸していくのかを理解するための強力なツールとなるでしょう。

図2 左図: 半値全幅とピーク速度の関係。
OI] 6300˚A線プロファイルをマルチガウス分解した結果得られた、狭い低速度成分(NLVC)
線プロファイルをマルチガウス分解したもの。灰色のプラス記号は観測されたNLVC [71]を示す。青丸と赤三角
はそれぞれ光蒸発モデル[18]とMHD風モデル[18]によるNVLCを示す。右図
パネル。図2と同じだが、2.12μmにおけるo-H2 1-0 S(1)のNLVCの場合。灰色のプラス
は観測されたNLVCを示す[70]。青丸は、図と同じ物理的な
青丸は、図2と同じ光蒸発風モデルに対して、熱化学コードで後処理をした結果です。
の結果を示す.
惑星形成ディスクにおける光蒸発のモデル化
概要
若い星を取り巻くガスとダストの円盤から惑星が誕生する。
惑星は、若い星を取り囲むガスやダストの円盤から生まれる。中心星からの高エネルギー放射は、円盤の大気から熱流出を引き起こし
円盤の大気から熱流出し、円盤や惑星系の進化に大きな影響を与える。
円盤と惑星系の進化に強い影響を与える。このような背景から、様々な複雑さを持つ数値モデルが開発され
このような背景から、中心星から円盤が光蒸発する過程を研究するために、様々な複雑さを持つ数値モデルが開発されている。
我々は、数値計算の手法、結果、そして現在のモデルの予測性
また、これらのモデルを制約するための観測的なテストについて述べる。
1 はじめに
惑星系の形成と進化は、惑星系を構成する天体の進化と最終的な散逸と強く結びついている。
惑星系の形成と進化は、それらが形成される原始惑星系円盤の進化と最終的な散逸と強く結びついている。
これは、中心星からの照射によって、加熱、電離(したがって磁気的な変化)、そして
加熱、イオン化(つまり磁場との結合)、そして原始惑星系を分散させる熱流の引き金となる
熱流出が起こり、円盤の物質が拡散する。
ガス円盤の拡散は、巨大惑星が形成されるまでの最終的なタイムスケールを決定するものであり
巨大惑星が形成される最終的なタイムスケールを与え、惑星系の最終的な構造にとって非常に重要である。
惑星系の最終的な構造にとって極めて重要です。光蒸発の仕組みは、まず円盤に隙間を開け
2 惑星形成円盤における光蒸発のモデル化 これは、移動する惑星に自然な駐車メカニズムを提供し[1-4]、また円盤後の軌道の力学的進化に影響を与える[5
軌道の進化に影響を与える[5, 6]。巨大惑星集団の最終的な半長軸分布は
巨大惑星集団の半長軸分布は、円盤の質量放出プロファイルに極めて敏感である [2, 3] 。
に非常に敏感である [2,3]。
惑星形成の初期段階における光蒸発の役割、例えば
惑星形成の初期段階、例えばストリーミング不安定性による準惑星の形成における光蒸発の役割については、代わりに議論されている
[7, 8]. ストリーミング不安定性が起こるためには、ガスに対する固体の割合が高いことが必要である。
必要である.光蒸発は、ガスを優先的に除去し、局所的にダスト/ガス比を増加させるメカニズムとして、通常、引き合いに出される。しかし
[7] はこの仮説を検証し、光蒸発が惑星全体の質量に与える影響はほとんどないことを明らかにしました。
7] がこの仮説を検証し、惑星の総質量に対する光蒸発の影響は無視できるとしたのに対し、逆の結論が
[8]では逆の結果が得られています。この不一致の理由は、光蒸発による質量減少のプロファイルの違いにあります。
光蒸発の質量損失プロファイルの違いにある。
現実的な質量損失分布は、惑星や円盤の人口合成モデル[e.
また、惑星や円盤の人口合成モデル[9-11]では、熱力学的な密度分布と一致する円盤表面の
熱力学的な風構造と矛盾しない円盤表面密度分布は、遷移円盤の観測結果を解釈する上で
遷移円盤の観測[12-15]やガス輝線・塵の観測[16-20]の解釈にも重要である。
線とダストの観測[16-20]を解釈する上で極めて重要です。
このような背景から、惑星形成円盤における光蒸発過程の理論的・数値的モデルが長年に渡って開発されてきました。
その主な目的は、空間分解された正確な質量放出率
質量損失率を正確に求めることを主目的としている。
最近の理論的・観測的な進歩 [レビュー 21, 22] によれば
最近の理論や観測の進歩により、熱風(光蒸発風)に加えて磁気風(MHD風)を指摘する
最近の理論・観測の進歩により、熱風(光蒸発風)に加えて磁気風(MHD風)の存在が指摘され、熱風の定量的予測モデルの開発が急務となっています。
観測で区別するために、定量的に予測可能な熱風モデルを開発する必要性を高めています。
を区別するために、定量的に予測できる熱風モデルの開発が急務となっています[18, 23]。このことは
MHD風とディスクからの角運動量抽出の関連性を評価するために最も重要である。
この論文では、数値光蒸発モデルの現在の地位をレビューする。この論文では、光蒸発の数値モデルの現状をレビューする。
特に、異なるモデルの適用性、および、結果の分岐に注目する。現在および将来の
観測によるモデルの検証についても述べる。
2 数値モデリング
円盤光蒸発は、放射伝達、熱化学、流体力学、ダストダイナミクスの連成問題である。最近まで、これらの効果を
しかし、近年、そのコードと数値計算能力が明らかになりつつあります[24,25]。
24, 25] が利用可能であることが示されています。
放射伝導 理論的な光蒸発モデルは、次の3つのうちの1つ、またはその組み合わせに対して開発されてきました。
理論的な光蒸発モデルは、恒星スペクトルの3つの異なる部分の1つまたは組み合わせに対して開発されました。
遠紫外線(FUV)6eV < hν < 13.6eV、極紫外線(EUV)6eV。
極端紫外線(EUV), 13.6eV < hν < 100eV; およびX線, 100eV < hν < 10keV
(特に軟X線は100eV < hν < 1keV)。それぞれ
の特徴や数値的な課題があり、これらを区別することが重要である。
区別することが重要です。
EUV放射
EUV光は、原子状水素を電離するのに十分なエネルギーを持つ光と定義され
を電離するのに十分なエネルギーと定義されている(hν > 13.6 eV)。中性水素の電離断面積は10^-17cm^2atomなので
中性水素の電離断面積は10^-17cm^2atom^-1であるため
であるため、EUV光子は、中性水素のカラム密度
中性水素の柱密度 NH = 10^17 cm^-2 を通過すると吸収される。
. EUV光と水素原子の相互作用は単純である。
光子と水素原子の相互作用は単純である。光子は吸収され、電離した水素原子が生成され、熱エネルギーが発生する。電離した領域での典型的な温度
電子-イオン対の生成は、再結合により相殺される。電子が基底状態になると、13.6e以上のエネルギーを持つ光子
が生成され、これがさらに媒質をイオン化し、拡散磁場を生成する。一方、励起状態への再結合は、電離光子の破壊につながる。
イオン化した光子は破壊される。の中心星から照射された場合。
の中心星から照射された場合、中心星からの光子は内部円盤の上に約10^4Kの高温静水圧大気を発生させる。このとき
この大気からの再結合光子の拡散場が、外層円盤を照射し
外側の円盤を電離させる。この問題は、2次元の輻射伝導として解かなければならない。
この問題は、直接電離場と拡散電離場を考慮した2次元放射伝達として解く必要があり、光電離問題を解くと同時に
この問題は、光電離の問題を解決しながら、直接電離場と拡散電離場を考慮した2次元放射伝達として解く必要がある。
FUV放射
FUV光子は、6~13.6eVのエネルギーを持ち、水素を電離することはできません。
水素をイオン化することはできませんが、水素分子、CO
などを光分解し、炭素を電離する。塵埃からの光電加熱
と多環芳香族炭化水素(PAHs)からの光電加熱が、FUV光子の主なガス加熱メカニズムである。
による光電加熱が主流である。加熱は粒子表面に比例する。
したがって、円盤大気中に小さな粒やPAHsが豊富に存在する場合、FUVはガスを加熱する。
FUVはガスを加熱し、熱風の駆動に寄与する可能性がある
[26]. ガスが放射するエネルギーは、ダストが処理するエネルギーの1%未満に過ぎません。
ガスが放射するエネルギーは、ダストが処理するエネルギーの1%以下であり、主に小さなダスト粒やPAHからの光電子によって衝突的に加熱される
やPAHsからの光電子、あるいは振動励起したH2によって主に衝突加熱されます。そのため、その温度は
ダストの進化と化学の両方から影響を受けます [24, 27]。FUV光子は、主にHとH2の中性層を
中性HとH2の層を10 -5000 Kの温度まで加熱することができます。
フラックスの大きさ、ガスの密度、化学的性質に依存します。
この問題を正しくモデル化するためには、2次元の放射伝導と、密度や温度の激しい変化を考慮した十分に大きな化学ネットワーク、そして適切なダスト進化モデルを組み合わせる必要があります。もう一つの複雑な問題は
は、降着による恒星のFUV磁場成分が
が色球成分よりも大きいという事実があります。これは
ということは、円盤に到達するFUVフラックス、ひいては風の質量損失率は
降着率に強く依存し、降着率は時間とともに減少し、内部空洞が形成されると完全に停止します。
この降着速度は時間とともに減少し、内腔が形成されると完全に停止する。
X線放射
X線は大きく分けて、軟X線(100 eV < hν < 1 keV)で吸収され、円盤上層を加熱して熱風を起こすものと、硬X線に分けられる。
で吸収され、円盤上層を加熱して熱風を起こす軟X線と、硬X線
(1 keV < hν < 10 keV) は、円盤のずっと深いところまで到達し、塵とガスが熱的に結合する。
硬X線(1keV < hν < 10keV)は、塵とガスが熱的に結合している円盤のずっと奥まで届くが、電離度を高めることができる。
(硬X線(1 keV < hν < 10 keV)は、ダストとガスが熱的に結合している円盤の深部にまで到達するが、円盤中間面付近では(宇宙線と一緒に)電離度を高め、ガスと円盤磁場との結合に影響を与える。X線
X線光子の主な相互作用は、原子や分子の内殻の光電離である。
水素を含む)二次的な電離を引き起こし、次に一次電子と二次電子の運動エネルギーによる熱化。
X線加熱は、高密度のX線PDRでは数百K、低密度のX線PDRでは数十Kの温度域を生じます。
X線加熱は、高密度のX線PDRでは数百Kから、円盤上層では10^4Kの温度範囲を生じます。X線ルミノシティー
は星降着率に依存せず、最初の数年間はほぼ一定であり [28]、風による質量放出率が一定であることがわかる。
X線輝度は恒星降着率に依存せず、最初のMyrsでは時間に対してほぼ一定であり [28]、ディスクの表面密度の変化に関係なく、一定の風速の質量損失率が得られる。
2.1 方法
円盤光蒸発の重要性が認識された30年以上前 [29] から
30年以上前 [29]、この問題は、放射伝達モデル、あるいは
輻射伝導モデリングや時間依存の輻射流体力学に重点を置いてこの問題に取り組んできた.
ディスク光蒸発の最初の研究は、強いEUV放射体であるOB星によるディスクのEUV光蒸発に焦点を当てたものであった。2つのモデルライン
が同時期に開始された。一つは、エディントン近似による簡略化された放射伝達計算を採用したもの(3次元の放射伝達問題を
三次元の放射伝達問題を、恒星から鉛直上方に来る「3本の流れ」近似にする。
円盤の各点で鉛直上方、下方から来る "3つの流れ "に近似する)を採用したものである。
を、鉛直静水圧円盤に適用した [30, 31]。2つ目は、より力学に焦点を当てたもので
2次元流体力学光電離コードを開発することから始まりました。
コードを開発することから始まり、後に紫外線による塵の散乱の効果を含めて改良されました [34]。どちらの研究でも
どちらの研究でも、風に対する最も重要な寄与は
からの拡散場であること、そして熱風が重力半径は重力半径Rg1の外側にあることがわかった。EUVによる質量損失率を円盤半径の関数として解析的に定式化したものを加えることにより
光蒸発による質量損失率を、1次元の円盤粘性発展方程式のシンク項として解析的に定式化し
[37, 38]に追加することで、いわゆる「EUVスイッチ」が実証された(セクション3参照)。
最初のEUV光蒸発の流体力学的モデルは、T Tauri星
39]は、等温状態方程式を仮定し、流れの底の密度を以前の結果[31]から仮定して行われました。その結果、光蒸発流は重力半径よりもずっと小さな半径から亜音速(約0.3 cs)で打ち上げられることがわかった。
重力半径(Rc ' Rg/5)よりもはるかに小さな半径から亜音速(∼0.3 cs)で立ち上がることを発見した [36も参照のこと]。
これは解析的処方からは予想されないものであった。
これらの研究に続いて、T-TauriからのX線照射の最初の静水圧モデル
最初は単純な加熱モデル [40]、後に、より現実的な2次元モンテカルロ計算による
より現実的な2次元モンテカルロ光電離・ダスト放射伝達コード [41, 42
放射伝達コード [41, 42] を用いて行いました。後者の計算では、より現実的な
EUVとX線の両成分を含むより現実的な入力スペクトルを用いた計算を行った結果
後者の計算では、後者が完全に支配的であり、質量損失率が2桁ほど高くなることが示されました。
X線が支配的であることを示した。
同時に、EUV、X線、FUVを含む1+1次元静水圧平衡モデル、および包括的な化学ネットワークも開発された
[26, 43]. これらのモデルは、FUV放射がディスク外側の物質を除去するのに有効かもしれないが、それはディスクにPAHが豊富にある場合のみであることを示した。しかし
しかし、これらのモデルで使われた入力スペクトルは非常に理想的であり、硬X線の入力スペクトルは効率が悪い。
硬X線の入力スペクトルであり、ガスを加熱し、風を駆動するのには非効率的であった。
風を起こすには不十分でした。
これらのモデルは、適切な流体力学的計算をすることなく、すべて
という仮定で局所的な質量損失率を推定していました。
と仮定して局所的な質量損失を推定した。
いわゆるρc˙s法である。流体力学を用いない場合、風の基部を特定するのはかなり恣意的であり
流体力学がなければ、風の根元の特定はかなり恣意的であり、著者によって異なるアプローチをとっていたため、両者の緊張はさらに高まった。
このことが、モデル間の緊張をさらに高めることになった。X線とEUVの両方を含む最初の(放射線)流体力学計算[44, 45]は、詳細な熱処理から得られたイオン化パラメータを関数としてガス温度をパラメータ化することで行われました。
EUV放射[44, 45]を含む最初の(放射線)流体力学計算は、mocassinコードで行った詳細な熱・イオン化計算[42]から得たイオン化パラメータの関数としてガス温度のパラメータ化を用いて行った。
mocassinコード[46-48]を用いて行った詳細な熱・電離計算[42]から得られた電離パラメータの関数としてガス温度をパラメータ化して行った。
イオン化パラメータは、ξ = LX / nr2 、ここでLXはX線光度、rとnは局所的な円盤の半径とガスの体積密度を表します。この
この方法は、一般に ξ - Te 法として知られている。これらの研究は、後に
現代の流体力学コードpluto [49]を用いて拡張され、円盤の減衰効果をよりよく考慮するようになりました。
柱密度に依存するξ - Teパラメタリゼーションを用いて円盤の減衰効果をよりよく考慮した[50-53]。この改良された処方箋により
X線照射が数百auに達する可能性があること、また、高輝度X線の質量損失率が
高輝度X線の質量損失率は、より高エネルギーな光子が低輝度X線を加熱できないため、プラトーに到達する。
X線照射は数百auに達し、高エネルギー光子が円盤の低密度の冷たい領域を加熱できないため、高X線光度での質量損失率はプラトーに達することが示された。
ξ - Te 法の利点は、詳細な多周波熱計算に基づいていながら
多周波熱計算をベースとしながらも、流体力学の計算オーバーヘッドをほとんど発生させないことです。
この方法の利点は、詳細な多周波熱計算に基づいているにもかかわらず、流体力学の計算オーバーヘッドをほとんど発生させないことです。この手法の欠点は
熱計算が放射平衡で行われるため、断熱冷却の寄与が考慮されないことである。ξ -Te 法で行ったすべてのモデル
したがって、ξ -Te 法を用いたすべてのモデルは、放射平衡が正当であることを保証するために、事後チェックを行う必要があります。
を行い、シミュレーション領域全体で放射平衡が成立していることを確認する必要がある。これは
このことは、この手法で得られた全てのモデルで実際に実証されている
これまでのところ[44, 50-53]である。
最近、いくつかの数値実験が行われ、(非常に合理的な)放射伝達と
非常に合理的な)放射伝達と熱化学計算をオンザフライで行う数値実験が行われました。
を流体力学モデルで実行する数値実験が行われている[24, 25]。このアプローチは計算コストが高いため
このアプローチは計算コストが高いため、限られたスペクトルや空間分解能のモデルしか存在しません。
のみである.これらのモデルで得られた結果は、ξ - Te法で得られた結果と強く乖離しています。
これらのモデルで得られた結果は、3.1節で議論したように、ξ - Te 法で得られた結果と強く乖離している。
3 結果
これまでに開発されたすべての光蒸発モデルの主な結果は以下の通りである。
中心星からの放射が原始惑星系円盤の上層を加熱する。
原始惑星系円盤の上層部は、中心星からの放射によって加熱され、熱流として遠心力により加速され、原始惑星系円盤は拘束を解かれ
熱流で遠心加速される。風の質量放出率は、原始惑星系円盤の特定の
重力半径と呼ばれる円盤の特定の半径付近でピークを示し、そのプロファイルは多かれ少なかれ大きな半径に
を持つ。星に近い領域では質量放出が起こらないことが予想される
星に近い領域、つまり重力的に拘束されている領域からは質量放出が起きないと考えられる。
そのため、ガスを逃がすには非常に高い温度が必要となる。そのため
光蒸発による定常的な質量放出と、時間とともに定常的に減少する降着率の組み合わせが
光蒸発による定常的な質量損失と、粘性降着円盤における定常的な降着率の減少の組み合わせにより、いわゆる
光蒸発スイッチと呼ばれるものです。円盤が粘性的に進化するのは、数百万年前までである。
円盤は数百万年、あるいは粘性降着速度が風の質量損失率と同程度になるまで粘性進化する。
粘性降着速度が風の質量損失速度に匹敵する値に達するまで、円盤は数百万年間粘性的に進化し、その時点で光蒸発が起こり、円盤は内側から急速に分散する。
光蒸発が起こり、円盤は内側から外側へ急速に拡散していく。
空洞が形成される。
現代の光蒸発の流体力学的モデルは、(少なくとも)
しかし、惑星を含む3次元シミュレーションについては54を参照のこと]。
のみで行われ、その間に流出の定常解が得られる(理想的には)。円盤の表面密度の進化をモデル化すると
円盤の表面密度の変化をモデル化することは
一般に2次元流体力学的な計算では実現不可能です。そこで
は、2次元定常解を用いて、一次元質量損失プロファイルΣ˙ w(R) [37, 38, 55, 56]を決定し、これを一次元のシンク項として
を1次元の円板粘性発展方程式 [57, 58] にシンク項として加える。
にシンク項として導入し、時間の関数として円盤の表面密度進化を調べる。
∂Σ/∂t = 1/R ∂/∂R (3R^1/2 ∂/∂R(νΣR^1/2)) - Σ˙ w(R, t). (1)
図1、1Mの質量放出プロファイル(右図[52])と、それに対応する表面密度の変化(左図)を示す。
表面密度の変化(左図)を示す。表面密度進化(ギャップが開く時間と場所、拡散のタイムスケールなど)は、Σ(˙ R)
Σ(˙ R)に非常に敏感であり、このことは円盤内で形成される惑星の最終的な構造にも影響を与え [1-3]、また光蒸発による
ストリーミング不安定性による準惑星形成の引き金となる可能性もある [7, 8]。

図1 左図は、太陽質量の恒星の周りを回るMd=0.1Mの円盤について、円盤半径の関数としての1次元表面密度進化を示したもの。
太陽質量の星を周回するMd=0.1Mの円盤の場合。
[52]. 異なる線は[0, 25, 50, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 90, 99]の位置に描かれている。
%で描かれている。点線は、光による内部ギャップ開口部のおおよその位置
点線は光蒸発による内部ギャップの開口部のおおよその位置を示す。右図では、対応する
光蒸発による表面密度質量損失率を円板半径の関数として示している。
3.1 結果の乖離
上記のような大まかな図式はほとんどの著者によって共有されているが、各プロジェクトで導出された
Σ˙ w(R)と、異なるプロジェクトで得られた風の物理的性質
(例: 表 1 参照) は大きく異なっている。最近行われた、異なるモデル間の表面
密度質量損失について、円盤光蒸発の異なるモデル間の比較 [22,
図7参照]は、円盤光蒸発の異なるモデル間における表面密度質量損失の桁違いを明らかにした。
累積質量損失率に一桁の差があることが明らかになった。
これは、表面質量損失率の最大値の位置だけでなく、プロファイルの範囲にも依存する。これらの
これらの違いは、恒星の照射に採用した周波数帯の
この違いは、恒星照射に用いた周波数帯の選択と、使用した手法の違いによって大まかに理解できる。
を用いた。しかし、ほとんどの場合、10Åの範囲にピークがあり、表面密度質量損失率は緩やかに減少し
しかし、その多くは10au付近にピークを持ち、外側の領域では表面密度質量損失率が緩やかに減少している。
光蒸発は恒星からの照射によって起こるので、このような
光蒸発は恒星の照射によって駆動されるため、乖離の大部分は、異なる著者によって仮定された入力スペクトルを考慮することによって理解することができる。
の議論も参照)。純粋なEUVモデル
[e.g. 60, 61] は、10^4 K付近の温度でほぼ等温のガスを生成する。
この場合、質量放出は重力半径付近でピークに達し、1Mの星では約
この場合、質量放出は重力半径付近でピークを示し、その値は1Mの星で約9au、全質量放出はEUVの平方根としてスケールし
の平方根に比例し、10^41 phot/secのEUVフラックスと仮定すると、およそ10-10 M/yrとなる。
[60, 61].
軟X線は、EUVよりもディスクの深い部分を透過するため
軟X線はEUVよりも深く透過し、古典的なEUVモデルよりも1〜2桁高い質量損失率が得られる。
軟X線は、EUV放射よりも深く円盤を透過し、古典的なEUVモデルよりも1〜2桁高い質量損失率をもたらす。
のX線輝度にほぼ線形に依存し、古典的なEUVモデルよりも1〜2桁高い質量放出率を得ることができる [45, 50, 52]。X線光蒸発モデルには、すべて
X線光蒸発モデルは、EUV成分を含むが、風の駆動には無関係であることを発見した [42など]。1M星のモデルでは、ソフトスペクトルと1030erg/secのX線ルミノシティを仮定すると、10-8M/yrの質量放出速度が得られた [44, 50]。X線による質量損失のプロファイルは、EUVの場合よりもはるかに拡張され、重力半径付近でピークとなる
重力半径付近をピークに、約200auまで広がっている。炭素は
X線は主に炭素の内殻に吸収されるため、X線不透過の主要な要因の一つである。
X線は主にガスやダストに含まれる重元素の内殻に吸収されるため、炭素はX線不透過の主要な要因の一つです。
の内殻に吸収されるからです[62]。炭素の枯渇は、円盤の進化に伴う自然な結果として予想されます。
炭素の減少は、炭素がCOからより複雑な種に変化する化学的進化と、炭素の大部分を氷の中に閉じ込める粒成長による物理的進化の両方から、円盤進化の自然な結果として予想される。
炭素の枯渇は、円盤の進化に伴う自然現象であると考えられる。炭素が枯渇した円盤では、その質量損失の大きさと範囲は
質量損失率の大きさと範囲は、炭素が枯渇した円盤では、ファクター∼2倍に増加すると予想される [51]。内部
FUV放射が円盤のさらに外側から光蒸発を引き起こすと予想される。
26]の静水圧平衡モデルに基づいた初期見積もりでは
の静水圧平衡モデルに基づく初期見積もりでは、多環芳香族炭化水素(PAH)の光蒸発が非常に効率的であることがわかった。
多環芳香族炭化水素(PAHs)が円盤の大気中に豊富に存在するとの仮定で、非常に効率的であることがわかった。しかし
T-Tauriディスクではほとんど観測されないPAHsの大気中存在量
[63]ではほとんど観測されず、さらに恒星のFUVフラックスは中心星への降着率に依存するため、大気中のPAHsは非常に小さいと考えられる。
に依存し、時間とともに減少する。これらの理由から
は、最終的な円盤の拡散にどのような役割を果たすかは不明である。
より最近の計算 [25] では、EUV、FUV、X線
を同時に考慮した最近の計算 [25]では、直接のEUVフラックスが風の駆動を支配しているという結論に達しています。
しかし、その結果、EUVだけを使ったモデルよりも2桁も高い質量放出率という結論に達しました。
これらの計算は恒星からの直接のEUV光は、円盤の内側で吸収され
を吸収し、膨張した円盤の内側から来る拡散磁場が光蒸発を促進するという古典的な描像とは対照的です。
光蒸発は重力半径の範囲内で(低速で)行われる。
EUVが直接届くと仮定した場合、重力半径を超えたところでも光蒸発が起こる。
重力半径以上ではEUVの直接照射が可能であるという仮定は、過去の計算に基づくものである[64]。この計算と過去の計算との間の矛盾の原因は、次のような点にあると考えられる。
この計算では、円盤の内側が外側の領域を遮蔽するほど膨張していない。
ディスクの内側が外側の領域を遮蔽するほど膨張しない場合や、大きなフレアリングがある場合など。
は、ほとんどのディスクに当てはまらないかもしれない[65]。最後に、これらの結果は
は、詳細な2次元モンテカルロRTと熱計算を行った先行研究[42]とも矛盾しない。
モンテカルロRTと静水圧円盤の熱計算によって、EUVの役割を明確に検証している[42]。
観測的に得られたX線スペクトルの存在下でEUVの役割を明示的に検証し、最終的な質量損失率にEUVの効果が無視できることを見出した。A
しかし、最終的にこの矛盾の原因を明らかにするためには、専門家による詳細な比較を行う必要があります。
この不一致の本質を明らかにする必要がある。
また、最近の計算[24]で得られた風の物理的性質
最近の計算 [24] では、Athena++コード [66, 67] を用いて自己無撞着な輻射流体計算を行い
を用いた自己無撞着な輻射流体力学と光電離円盤の熱化学計算による計算 [24] と、ξ -Te アプローチを用いた計算 [44, 45, 50, 52] との間に強い乖離がある。
また, 風の物理的性質についても強い発散が見られる.
最近の計算 [24] では、Athena++コード [66, 67] を用いて自己無撞着な輻射流体計算と光電離円盤の熱化学計算を行った結果、ξ -Te 法を用いたモデルと比較して
を用いた自己無撞着な輻射流体力学計算や光電離円盤の熱化学計算を行ったモデル [24] と、ξ -Te アプローチを用いたモデル
[44, 45, 50, 52, 53]. 得られた全質量損失率は同程度であったが
Athena++モデルは、X線放射は風の駆動に非効率的であるという結論に達し
であり、EUVが支配的であるという結論を得た。また、風の温度構造も
の温度構造も両者で大きく異なる。Athena++モデルでは、風の根元で非常に高い温度(10^5K)が予測され、上空に行くほど温度が下がる
Athena++では風の根元が10^5Kと非常に高く、上へ行くほど低くなる。
ξ - Teモデルで得られたパーカー的な風とは対照的である。
10^4Kに達するが、それは風のごく限られた領域だけである。
しかし、それはEUV放射によって加熱される(発射されない!)風の非常に限られた領域だけである。これらのモデルの乖離は
これらのモデルの相違は、しばしば、放射伝達と熱平衡へのアプローチ方法に関する方法論の違いに起因するとされてきました。
放射伝達と熱平衡へのアプローチの仕方、採用する照射スペクトル
を選択し、ガスを冷却するために利用可能なプロセスの違いに起因している。最近の詳細な比較 [68] によって、この問題に光が当てられ、以下のことが示された。
これらのモデル間の乖離は、主に照射スペクトルの選択によるものであり
照射スペクトルの選択と、非常に限られた数の周波数点によって引き起こされていることを明らかにした。
と比較して、Athena++モデル(7)では、放射場を記述するために使用される周波数点の数が非常に限られている。
ξ -Te モデル (>1000) と比較して、Athena++ モデル (7) では照射スペクトルの選択と放射場を記述するための非常に限られた数の周波数ポイントに起因する。ξ -Te モデルでは、T-Te のチャンドラ観測から得られた X 線スペクトルを用いています。
Chandra による T-Tauri 星の深い観測 [41, 53, 69] から得られた X 線スペクトルを用いているのに対し、Athena++ モデルは解析的な分布を仮定している。
モデルは解析的な分布を仮定している。
4 観測的検証
複雑な理論モデルが数値実験に留まることなく、自然現象の現実的な記述になるために
数値実験にとどまらず、自然現象の現実的な記述となるためには、複雑な理論モデルが
観測結果に対して検証可能な予測値を提供することが非常に重要である。この
この節では, 理論的な光蒸発モデルを制約するために用いられてきた直接的, 間接的なテストを列挙する.
光蒸発理論モデルを制約するために使用された多くの直接的および間接的なテストを列挙する.
4.1 直接的テスト
風は細く、そのガス成分を直接撮影することは不可能です。
しかし、風の気体成分を直接「観測」することは可能である
アウトフローで放出され、青くシフトした成分を示す輝線の高分解能分光法 [21, 22]によって、風のガス成分を直接「観測」することができます。衝突電離線
中性・低電離種([OI]、[NeII]、[SII]、[N2]、[FeII])の衝突イオン化線のプロファイル。
[FeII])、およびいくつかの分子トレーサー(COとH2)は、統計的に有意な数のT-Tauri星について利用可能です[e.g. 70-72]。観測されたプロファイルの大部分は
観測されたプロファイルの大部分は、X線駆動型光蒸発モデル
(16,17,73)であり,複合プロファイルを示す天体では,磁気駆動成分と組み合わせて
(図2参照)。サブミリ波領域の線(例.
COやCI)もまた、高傾斜天体の円盤風の存在を推測するのに使われてきた [74]。
また、数値MHD風モデルによる予測も存在します[75]。
による予測も存在する[75]。
風と円盤の大気領域における電離ガスも、自由電子を介することで
のような高空間分解能の観測装置を用いて、波長数cmの自由放射で検出し、空間的に拘束することができる。
ngVLA のような高空間分解能の観測装置による観測 [例
23]. これは、星に近い領域から吹いている磁気風を区別するための有望な方法である。
これは、光蒸発風よりもはるかに星に近い領域から駆動される磁気風を区別するための有望な方法です。
小さな(10μm以下の)塵粒は、打ち上げ領域からの風に巻き込まれる可能性があり [76-83]、高傾斜天体の散乱光観測、特に内部にダストキャビティを持つディスクから、そのサインを検出できる可能性がある [19-20]。
の散乱光観測で検出できるかもしれない[19, 20]。
4.2 間接的な検証
光蒸発モデルが一致すべき間接的な制約には、次のようなものがあります。
(i) 降着特性と表面密度の進化によって追跡可能な円盤の分散タイムスケールの観測結果。
観測された円盤集団の降着特性や表面密度の進化によって追跡できる。
を含む、観測された円盤集団の降着特性と表面密度の進化によって追跡できる、円盤分散の時間スケール [例えば 77, 84-89]; (ii) メタリシティ依存性
ディスク寿命の金属量依存性 [25, 62, 90-93]; (iii) 観測されたディスク集団の相関関係(M˙ - M?
M˙ - M?関係のような円盤個体群における観測相関[例えば94-96]。
ここで重要なのは、光蒸発モデルを検証するために、観測された円盤の個体数に対して風の性質
光蒸発モデルを観測された円盤集団に対して検証するためには、風の性質(円盤半径の関数としての質量損失率)を十分に広いパラメータ空間に対して計算する必要があることに注意する必要があります。
観測された恒星質量とX線の性質にまたがる十分広いパラメータ空間について計算する必要があることに注意してください。その際
その際、角運動量がどのように輸送されるかを仮定する必要がある。これまでのほとんどの
これまでの研究では、光蒸発と組み合わせた粘性モデルを仮定しています。このような研究を繰り返すことは興味深いことです。
磁化された円盤風による角運動量輸送を仮定したこの一連の研究は興味深いものです。
5 展望
前節の最後に述べたように、磁気化した円盤風は熱風と組み合わせて存在する可能性がある。
が熱風と混在して存在し、粘性に代わって角運動量輸送の支配的な機構を提供するかもしれない。
粘性の代わりに角運動量輸送の支配的な機構となるかもしれない。その存在を直接示すヒントが、いくつかの天体で観測された輝線プロファイルに見られます。
を観測したところ、複数の流出成分を示す天体があることがわかった [例えば、22,最近のレビュー]。さらに、非理想的な磁気流体力学モデルである
は日常的に磁化された風を観測していますが、磁気回転不安定性をディスクのほとんどの領域で維持するのに苦労しています[e.g. 59, for a recent review]。
レビュー]。明らかに、円盤風のモデリングのフロンティアは、この2つのプロセスを同時に、かつ十分な空間分解能で説明することであり、その結果、以下のようなモデルを作り出すことができる。
ということです。
最初の試みは有望である[e.g. 99, 100]が、それらはまだ、円盤の内側領域(観測されたほとんどの領域)における解像度が不十分である。
の解像度が不足しており,また,(ほとんどの観測結果が得られる)円盤内領域では
また,放射伝達を単純化しすぎたり,制約のない多くのパラメータに頼っているため
磁束とその変化を記述するために多くの制約のないパラメータに依存している。
その進化を記述するための多くの無制約なパラメータに依存している。これらの問題を克服することができれば、これらのモデルは
観測結果との比較に十分な予測力を得ることができる。
その結果、原始惑星系円盤の進化を理解するための強力なツール
原始惑星系円盤がどのように進化し、最終的にどのように散逸していくのかを理解するための強力なツールとなるでしょう。

図2 左図: 半値全幅とピーク速度の関係。
OI] 6300˚A線プロファイルをマルチガウス分解した結果得られた、狭い低速度成分(NLVC)
線プロファイルをマルチガウス分解したもの。灰色のプラス記号は観測されたNLVC [71]を示す。青丸と赤三角
はそれぞれ光蒸発モデル[18]とMHD風モデル[18]によるNVLCを示す。右図
パネル。図2と同じだが、2.12μmにおけるo-H2 1-0 S(1)のNLVCの場合。灰色のプラス
は観測されたNLVCを示す[70]。青丸は、図と同じ物理的な
青丸は、図2と同じ光蒸発風モデルに対して、熱化学コードで後処理をした結果です。
の結果を示す.




















※コメント投稿者のブログIDはブログ作成者のみに通知されます