回転するダンベル形状の表面重力

接触小惑星の細いところを小脇に抱え千切っては投げ千切っては投げのサンプル採取が夢の私としては、接触連星形状の彗星や小惑星が自転すると遠心力と重力で表面ではどちら向きに力が掛かるのか興味があります。以下、自動翻訳。
回転するダンベル形状の表面重力

回転する天体（彗星や小惑星など）の形状を、それ自体の重力場の下で決定する問題を調査します。より具体的には、対称軸に垂直な2番目の軸を中心に回転する1つの軸（ダンベルなど）に関して対称なオブジェクトを検討します。オブジェクトは、一定の質量密度の非圧縮性流体としてモデル化できると仮定します。これは、粒子の集合体の最初の近似と見なされます。
文献では、物体の重力場は、球座標を含む多重極展開として説明されることがよくあります（Kaula、1966）。この作品では、体の対称性に最も自然に適応する円筒座標で形状を記述し、回転体によって生成される重力ポテンシャルを楕円積分で簡単な式として表現します。平衡形状は、重力ポテンシャルエネルギーと体表面の回転運動エネルギーのバランスが取れたときに発生します。このような平衡形状は、最適化問題の解として導き出すことができます。これは、変分法によって見つけることができます。この方法をダンベル形状の2パラメータファミリに適用する例を示します。
キーワード：ポテンシャル論、惑星重力、太陽系、小惑星、数学的天文学、軸対称天体、ダンベル。

図1：z軸周りの回転体の矢状断面。 すべてのポイント
オブジェクトの内部は−z0≤z≤z1の範囲内にあります。 固定zの場合、点は半径smaxの円盤。


図2：zでの表面ポイントの円形領域を示す回転ダンベル。


図3：関数f（z）によって与えられる形状の例。これは式（20）で次のように定義されます。


図4：ω= 0.1およびω= 0.2、ω= 0.3およびω= 0.4の場合のおおよその平衡形状。


図5：ω= 0.5およびω= 0.6、ω= 0.7およびω= 0.8の場合のおおよその平衡形状。


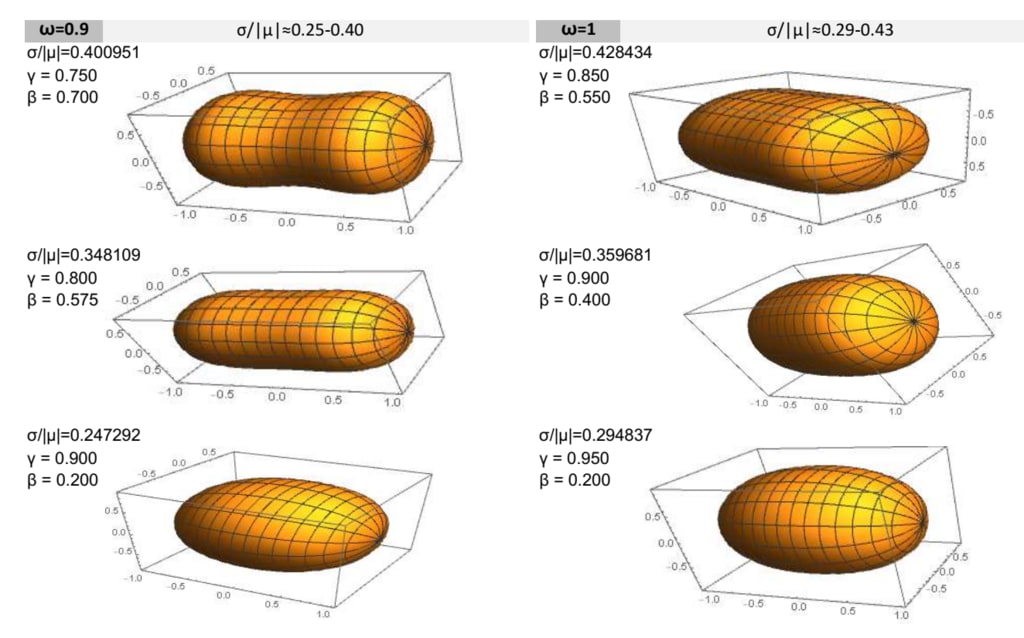
図6：ω= 0.9およびω= 1.0の場合の近似平衡形状。