
オールトの雲内の小彗星は宇宙線によるイオン化でエネルギーが蓄積され、化学反応が一気に進むと爆発して表面を吹き飛ばす。太陽に近づかなくてもバーストする彗星は危ない。以下、機械翻訳。
オールトの雲での彗星の爆発
要約
太陽系外縁部の彗星の核には、常に低温の宇宙線が照射されています。
蓄積された高濃度のラジカルは、次の物質と急速に再結合する可能性があります。
彗星の表層が大幅に加熱される。 彗星の活動全体のモデルを提示します
ラジカルの再結合によって生じる太陽中心距離。 検討した結果、
このメカニズムは、たとえ太陽系の遠い領域でも彗星の活動を引き起こす可能性があります。
オールトの雲の距離。 遠く離れた彗星溜まりでの爆発は、新たな塵の発生源となる可能性があります。
宇宙で最近発見された異常な拡散光に寄与する氷の粒子
銀河系外の背景光。 オールトの雲の中の小さな半径の彗星の軌道は次のとおりです。
彗星の爆発の影響を大きく受けています。 この効果は、観察された
小半径の長周期彗星の数。
キーワード: カイパーベルト 彗星 宇宙線 氷
1. はじめに
太陽系の外側には、カイパーベルトとオールトの雲という 2 つの彗星核の発生源があります。 表面
彗星の温度は、カイパーベルトでは 30 ~ 60 K、オールト雲では約 10 K の範囲にあります。 気温が低いため、
彗星が太陽の近くで起こりがちな内部プロセス(水の氷の昇華など)は抑制されます。 いつ
低温における氷の化学的および物理的進化を考慮すると、宇宙線照射は重要な役割を果たします。
氷の性質を変える役割。 カイパーベルトでは、彗星の核に太陽宇宙線(SCR)が照射され、
変調された LIS (局所星間スペクトル) を備えた銀河宇宙線 (GCR)。 カイパーベルトのSCRフラックス
この領域は、太陽系の内部に比べて大幅に減少しています。 オールトの雲の中では銀河宇宙線が
LIS は常に彗星の表面を攻撃します。 高エネルギー粒子の照射によりラジカルやイオンが発生します。
低温の氷。 ラジカルの移動度は温度とともに大幅に低下するため、彗星の核は
太陽系の外側には高濃度のラジカルが蓄積する可能性があります。 実際、氷に陽子を照射する実験では、
電子、中性子、ガンマ光子は、温度 10 ~ 100K の氷中でラジカルが効率的に蓄積することを示しています。
(Moore et al., 1983; Carpenter, 1987; Shabalin et al., 2003; Zhu et al., 2021; Pavlov et al., 2022)。 ラジカルは高い
高温で反応するため、照射された氷の周囲温度がわずかに上昇しただけでも、瞬時に反応が起こる可能性があります。
ラジカルの発熱再結合 (Shabalin et al., 2003)。 また、ラジカル濃度が高いと不安定になります。
自発的組換えに至るまで(Shabalin et al., 2003)。 ラジカルの濃度が1%に達すると、照射された
サンプルはラジカルの再結合により突然発火する可能性があります (Moore および Hudson、1992)。
彗星は太陽に近づくと、太陽の中に放出された塵や氷の粒子に太陽光を反射して明るさを増します。
ハロー。 このプロセスは段階的である場合もあれば、突然である場合もあります。 後者は彗星の爆発と呼ばれます (Gronkowski、2007)。 彗星
爆発は約 3 天文単位の水と氷の昇華境界をはるかに超えて検出されています (Meech et al., 2009)。
非晶質から結晶質への氷の遷移は、からの距離での彗星の爆発の主な原因であると考えられています。
最大14天文単位の太陽。 しかし、最近では、太陽中心距離がはるかに遠い彗星、つまり C/2017 が検出されています。
K2 (PANSTARRS)、C/2010 U3 (Boattini)、および C/2014 UN271 (Bernardineli-Bernstein) は、他の
彗星の活動のメカニズム (Bouziani と Jewitt、2022)。 パブロフらでは、 (2022)、我々は、組み換えが
ラジカルの存在は、太陽中心距離が遠いところで彗星の活動を引き起こす可能性があります。 組換え反応が起こるので、
非常に低い温度では、彗星はオールトの雲の中でも活動を示すことができます。
ここでは、太陽系の遠方領域での彗星の爆発について考えます。 実現可能性を評価するには
太陽中心距離が遠い場所での彗星の活動を考慮して、我々は、彗星爆発によって引き起こされる彗星の爆発のモデルを開発しました。
フリーラジカルの再結合。 モデルについてはセクション 2 で説明します。数値シミュレーションの結果を示します。
セクション 3 で説明し、セクション 4 で説明します。結論はセクション 5 にまとめられています。
2. モデルの説明
2.1. 基本方程式
我々は、Prialnik と Bar-Nun (1987)、Orosei et al. の彗星の内部プロセスを記述するためのモデルを使用します。 (1999) と
マルブフら。 (2012年)。 リストされているすべてのモデルは、太陽中心距離で太陽に接近する彗星用に開発されました。
14AU未満。 照射中、フリーラジカルは彗星の上表層に常に蓄積されるため、
ラジカルを彗星の内部の再生可能なエネルギー源として扱うことができます。 フリーラジカルのまさにこの特徴により、
ラジカルの再結合は、太陽が届くほどの距離にある彗星の内部のプロセスの完璧な持続可能な原動力です。
放射線照射は大幅に減少する(Pavlov et al., 2022)。
私たちのシミュレーションでは、次の彗星の活動モデルを使用します。 ラジカルの再結合により、
層内の塵と氷の温度。 アモルファス氷から結晶氷への転移は約 120 K でゆっくりと始まり、
130 K では急速に進行します (Schmitt et al., 1989)。 アモルファス氷が揮発性ガスの分子を捕捉することはよく知られています。
(例: CO) 低温で (Bar-Nun et al., 1985)。 閉じ込められたガスの放出は、
アモルファスから結晶質への氷の転移。 ラジカルの再結合率が高く、ガス容量が大きいため
非晶質の氷から揮発性物質が放出されると、彗星の表面下に高圧ゾーンが生じる可能性があります。 ガスのとき
圧力が彗星物質の引張強度を超えると、高圧を超えると彗星層が破壊されます。
ゾーンは塵や氷の粒子の噴出によって発生します (Gronkowski および Wesołowski、2015)。
現在のモデルによると、彗星は揮発性ガスが効率的に凝縮して寒冷地で形成された。 の
実験的および理論的研究により、非晶質の氷が彗星の物質の大半を占めていることが示されています。 観測結果から、CO
そしてCO2ガスは彗星の昏睡中に水のほかに最も豊富な成分である。 したがって、私たちのモデルには以下が含まれます
彗星核の 4 つの構成要素: 塵、水氷、CO、CO2。 初期の氷の組成は次によって決まります。
塵と氷の質量比 𝜇 非晶質の氷に閉じ込められたガスの質量分率 𝑓𝑛(𝑛 = CO、CO2) と気孔率 Ψ。
彗星層の質量密度 𝜌 はすべての化合物の合計です。

どこで𝜌d、𝜌a、𝜌c、𝜌𝑛は、塵、非晶質の氷、結晶質の氷、および揮発性物質の質量密度です 𝑛 (c は
氷状態、v は気体状態) をそれぞれ表します。 水蒸気がエネルギーと局所ガス圧力に及ぼす影響
考慮される温度は重要ではありません。
彗星核の熱力学的進化は、全球エネルギー保存方程式に従います。
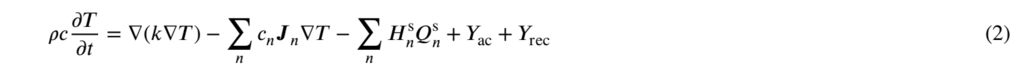
ここで、𝑐 は比熱容量、𝑘 は彗星物質の熱伝導率です。 𝑐 と
𝑘 は Marboeuf et al. に従って計算されます。 (2012年)。 耐火物にはエンスタタイトの比熱容量を利用します。
(ブジアーニとジュイット、2022)。 彗星物質の熱伝導率はヘルツ係数 ℎ に強く影響されます。
(Marboeuf et al.、2012)。 ℎ の一般的な値は 10−1 ~ 10−3 の範囲にあります。
式(2)の項は、 図 1 は、彗星層を通した熱拡散を示しています。 (3) 項は対流を表し、
どこで𝑐
𝑛 と 𝑱𝑛 は、それぞれ揮発性物質 𝑛 の比熱とガス流束です。 (4) 項はエネルギーを説明します。
昇華時の消費と凝縮時のエネルギー放出。ここで 𝑄s 𝑛 はガス源、𝐻𝑛s は潜在ガスです。
𝑛ガス昇華。 (5) 項は、非晶質から結晶質への氷の転移のエネルギーを表します。
閉じ込められたガスの昇華によるエネルギー損失を考慮します。

ここで、𝐻^cr は結晶化の潜熱、𝜆 は結晶化速度です (Schmitt et al., 1989)。 (6)項
ラジカルの再結合中に放出されるエネルギーを説明します。

ここで𝐻^rec 𝑥
𝑥,𝑁𝑥 タイプのラジカル 1 個あたりの再結合反応のエネルギーです。
ラジカルの濃度です
そして𝐾𝑥
組み換え率です。
ラジカルの再結合は、二分子の運動方程式に従います。

アレニウスの法則に従って、𝐾𝑥は温度 𝑇に依存します。

活性化エネルギー 𝑈a,𝑥 とボルツマン定数 𝑘b を使用。
このモデルでは、彗星物質の氷成分に含まれるラジカルのみを考慮し、ラジカルの次の反応を考慮します。

表面境界条件は次のようになります。式のここで、𝐴はボロメトリックボンドアルベド、𝜀は赤外線表面放射率、𝜎はステファン・ボルツマン定数です。

値 𝐹b
彗星核の外部加熱の考えられるすべての原因を説明します。 太陽放射が支配的になるのは、
距離𝑟h
最大10^3AU。 10^3 天文単位(オールトの雲)を超える領域では、宇宙マイクロ波の寄与
背景 (𝐹CMB)、銀河円盤放射 (𝐹disk)、および超新星または通過する明るい O、B 星の放射
(𝐹OB,SN) は (Stern と Shull、1988) を考慮する必要があるため、次のようになります。 2は次のとおりです。

𝐿sはどこですか
太陽の明るさです。
彗星層の組成の変化は、各成分の質量保存方程式を解くことで得られます。
非晶質から結晶質への氷の転移、ガス拡散、昇華/凝縮を考慮した彗星物質の解析:

揮発性物質のガス流量 (𝑛 = CO、CO2) によって与えられます:

どこ𝑃𝑛
は気体 𝑛 と 𝐺𝑛 の分圧です
はガス拡散係数です。 多孔質彗星を通るガスの流れ
物質は、クヌーセン数に応じて、1) 遊離分子 (クヌーセン領域)、2) 粘性、または 3) それらの混合物になります。
このモデルは、ねじれ度 √ を持つ円筒状の細孔を考慮しています。
Marboeufらに続く2件。 (2012年)。
式の表面境界条件は次のようになります。 13 は 𝑃𝑛 = 0 です。結晶氷の昇華は含まれていないため、
考慮された温度では重要ではありません。 粉塵の拡散も考慮していません。
非晶質の氷からの揮発性物質の放出は、局所的な圧力 (𝑃𝑛) がかかると不飽和状態を引き起こします。
)
飽和ガス圧力 𝑃 ^s 𝑛より大きいか小さい。 ガスによる飽和状態の再確立
結露(𝑃𝑛 > 𝑃 sの場合)
𝑛) または氷昇華 (𝑃𝑛 < 𝑃 s の場合)𝑛) よりもはるかに短いタイムスケールで発生します。
アモルファスから結晶質への氷の転移。 モデルは、凝縮/昇華の時間が次の場合に次のように仮定します。
モデルの選択されたタイムステップでは、飽和状態の再確立が瞬時に行われます。 の偏差
飽和圧力からの局所圧力を凝縮ガスの密度に加減算して保証します。
大量保存(Davidsson、2021)。
捕捉されたガスが非晶質の氷から放出されると、ガス圧力が上昇します。 プレッシャーは続く
アモルファス氷からのガス束が彗星を通過する拡散束とのバランスに達するまで増加する
層。 地下領域の圧力の値は、式 1 を使用して計算できます。 2-15. 地下圧力がかかると
彗星物質の引張強度を超えると、亀裂が生じる可能性があります。 この影響により激しい排出が起こる可能性があります
高いガス圧による空洞上の彗星の物質の観察 (Gronkowski と Wesołowski、2015; Prialnik と Sierks、2017)。
ここでは、地下圧力が引張強度を超えたときにバーストが発生すると仮定します。
数値計算では、式 (1) に対して有限体積法による完全陰的スキームを使用します。 1D の 2 と 13
球状の幾何学。 圧力と圧力の変化を制限するために、時間ステップは計算中に常に調整されます。
温度。
2.2. 初期条件とモデルパラメータ
ここでは、オールトの雲にある彗星の核を考えます。 オールトの雲の中の彗星の組成は次のようになりますが、
動的に観測された未知の「新しい」彗星は、オールトの雲にある彗星を表している可能性があります。 モデルは次のことをシミュレートするため、
宇宙線による効果的な照射が起こる彗星の上層の進化、以下にリストされるすべてのパラメータ
表層について説明します。 最初は、揮発性ガス CO と CO2
非晶質の氷の中に閉じ込められた状態でのみ存在します。 私たちは
この制約を使用して、このモデルを、太陽中心距離に基づく大きな彗星の活動のモデルと区別します。
揮発性氷の昇華について。 さらに、凝縮して閉じ込められたガスの昇華も同様の影響を与えます。
彗星の活動の総エネルギー (式 2 を参照)。 CO および CO2 ガスのモル存在量
水に対して
両方とも 10 % (つまり、CO と CO2 の質量比)
水氷まではそれぞれ 0.16 と 0.25)。 これらの値を選択したのは、
𝑓CO と𝑓CO2
理由は 2 つあります: 1) 高濃度でトラップされた揮発性分子により、アモルファスから結晶質が変化します。
氷転移エネルギーはニュートラル。 したがって、このモデルでは、組換え反応が彗星の活動の主なメカニズムとなります。
2) 星間 CO2 のモル存在量
氷は 10 〜 23% の範囲にあり、次の値とほぼ同じです。
CO (Gerakines et al., 1999)。 モデルでは、塵と氷の質量比は、氷が豊富な場合 𝜇 = 0 から氷が少ない場合 𝜇 = 4 まで変化します。
ケース。 Gronkowski and Wesołowski (2015) に従い、細孔半径は 1 𝜇m に設定されています。 強烈なGCR照射により、
彗星の上部層は、有機分子と塵が豊富に含まれた緻密な地殻を生成する可能性があります (Strazzulla と Johnson、1991)。
ここでは、照射によって生成された高密度の地殻が、気孔率の低い耐火物(有機物と塵)で構成されていると仮定します。
Ψ = 0.1、密度は 3000 kg m−3 に近い。 地殻の下では、彗星物質は非常に多孔質であると考えられています (Ψ = 0.65)。
シミュレーションで使用されるすべてのパラメーターを表 1 に示します。 67P/チュリュモフ-ゲラシメンコ ショーの観測結果
彗星は引張強度が数 Pa 程度の低強度天体になる傾向がある (Basilevsky et al., 2016)。 しかし、
長周期彗星の大規模な構造は、短周期彗星のそれとは大きく異なる可能性があります。 加えて、
引張強さは彗星の層の深さに依存する可能性があります。 シミュレーションでは最大推定値を使用します。
Gronkowski と Wesołowski に続く、彗星物質 10^4 Pa の大規模引張強度の研究 (Reach et al., 2010)(2015年)。
フリーラジカルは、1) 周囲温度が上昇したとき (再結合の誘発)、または 2) 次のときに活性化されます。
ラジカルの臨界濃度に達します (自発的再結合)。 モデルは誘発のみを考慮します
組み換え。 活性化エネルギーは
H ラジカルの量 (式 6) は 0.01 eV から 0.11 eV まで変化します (Flournov et al., 1962;Kirichek 他、2017)。
表1
モデルのパラメータ。 パラメータ値
彗星の半径 R、 10^3m
Ψ 0.65
𝑟𝑝、m 10^−6m
ℎ 10^−3−0.1
𝜖 0.96
𝐴 0.04
𝑓𝐶𝑂,𝑓𝐶𝑂2 0.16、0.25
初期温度𝑇0、K 10
ラジカルの初期濃度 𝑁0,𝑥 0 − 1%
𝑈a,H、eV 0.1 − 0.11
𝑈a、OH、eV 0.25
50 K を超える温度では、H ラジカルはヒドロキシルに比べて微量しか存在しません。
ラジカル。 OHラジカルは低温では安定であり、約100Kで活性化エネルギーを持って激しく反応します。
0.25 eV (Johnson および Quickenden、1997; Pavlov et al.、2022)。 ヒドロキシルラジカルの再結合は次の時点から始まります。
したがって、100 K 未満の温度での再結合速度は無視できます。 したがって、我々は考慮しません
私たちのモデルにおけるOHラジカルとHラジカルの相互再結合。 この反応のパラメーターは、次のことからほとんどわかっていません。
実験。 モデルによると、再結合を誘発するには彗星の層を少なくとも 1 ケルビン加熱する必要があります。
Hラジカルの。 式のパラメータ 6 つは (Pavlov et al., 2022) および (Flournov et al., 1962) からのものです。 での長時間照射
気温が低いと、彗星の表層に高い放射線量が蓄積されます。GCR(主に陽子)
彗星の表面から上部 10 メートルにエネルギーを効果的に蓄積します。 グロノフら。 (2020) 照射をモデル化
彗星の質量 (𝜌 = 538 kg m^−3)、𝜇 = 4) を GCR によって計算し、吸収線量プロファイルを取得しました。 彗星の特定の層
臨界値を超えない濃度でラジカルを蓄積することができます。 実験から、自発的に
陽子線が照射された水の氷中での再結合は、H ラジカルの濃度が約 1% (陽子に対して
水の氷の分子の数)(ムーアとハドソン、1992)。 陽子線照射によるHラジカルの発生量を利用
Moore and Hudson (1992) による非晶質氷 7×10^−3 eV−1 と、オールト雲の堆積線量率
(Gronoff et al., 2020)、臨界濃度の蓄積時間は 1 メートルで 10^2 Myr から 10^3 Myr まで変化します。
彗星の表面から10メートルの深さ。 彗星の核の最初の数センチメートルは臨界濃度に達します。
500 万年以内のラジカル。 この効果により、緻密な地殻の形成が促進される可能性があります。
このモデルでは、ラジカル分布の 2 つのプロファイルを使用します。 最初のプロファイルは、最高値が上昇した瞬間に対応します。
ラジカルの集中はダスト層の直下で達成されます。 2 番目のプロファイルは累積に対応します。
表面層のラジカルの平衡飽和濃度の変化(図1)。 Shabalin (1998) によると、飽和した
ラジカルの濃度は、低温での照射線量率に依存しない可能性があります。 その結果、上部は、
彗星の層には、同様の飽和濃度のラジカルが存在する可能性があります。 ここでは、上部 10 メートルのみを仮定します。
彗星の核は、オールト雲の進化中に高濃度のラジカルを蓄積します。
線量沈着率 (Gronoff et al., 2020)。 我々は、上部 10 メートルの初期温度勾配が次のようになることを提案します。
層は重要ではありません。 ラジカルの濃度が臨界濃度 (約 1%) に近いか、それ未満です。
上層10cmはラジカルのないダスト層です。
このモデルはラジカルの誘発再結合を考慮しているため、彗星の表面層は外部からの影響を受ける必要があります。
加熱して組換え反応を引き起こします。 非常に離れた領域 (つまり、オールトの雲) では、
彗星の軌道運動中の太陽放射の変化は重要ではありません。 ただし、近くの超新星や
O/B 星を通過すると、オールト雲内の彗星核が加熱される可能性があります (Stern と Shull、1988)。 スターンとシャル (1988) は示した
太陽の進化の間に、非常に明るい星(クラスOとB)がオールトの雲の近くを通過したこと
系 ≈ 4.5 Byr の結果、少なくとも 1 回の加熱イベントが発生し、各彗星の核の温度が上昇しました。
また、接近超新星により、オールト雲内のすべての彗星が周期的に 30 K まで加熱されます。 ラジカルを持つ層
これを行うには、𝑈a,H = 0.01 eV の場合は少なくとも 1 K 加熱するか、𝑈a,H = 0.11 eV の場合は温度 T = 30 K に達する必要があります。
Hラジカルの再結合を誘発します。
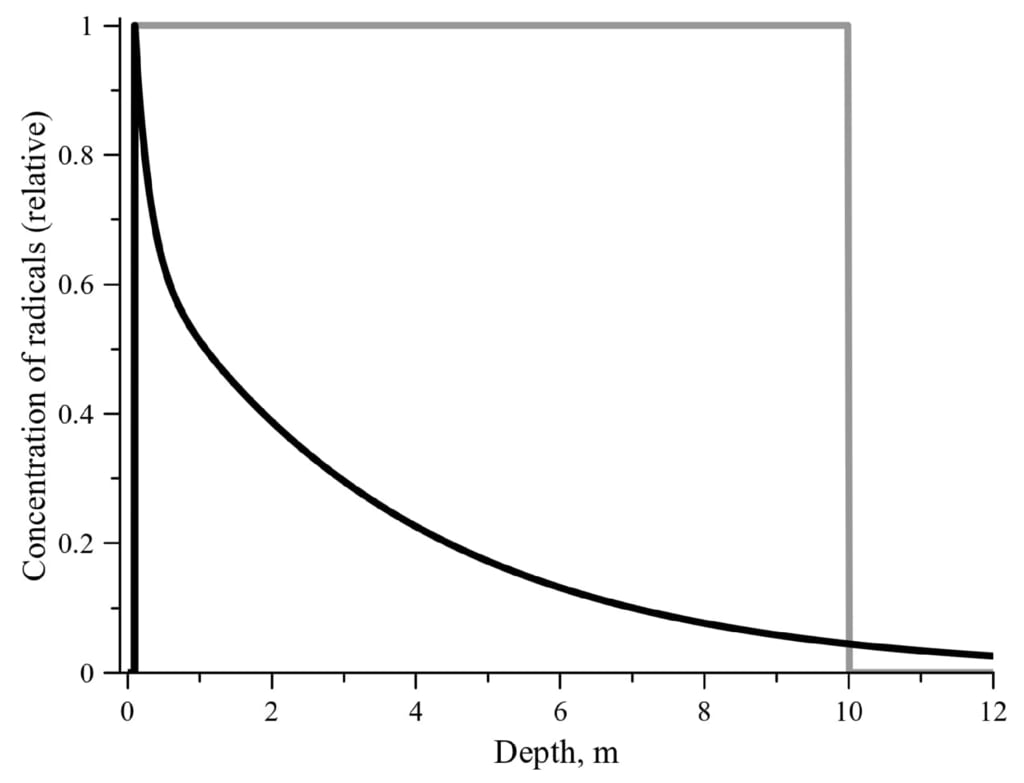
図 1: オールト雲にある彗星のラジカル分布のサンプル。 黒の実線は、
表面ダスト層の下の最大濃度 (1)。 灰色の実線の曲線は、ラジカルが発生したときのラジカルの分布を示しています。
飽和値に達します (2)。 線量沈着率は Gronoff et al. からのものです。 (2020年)。
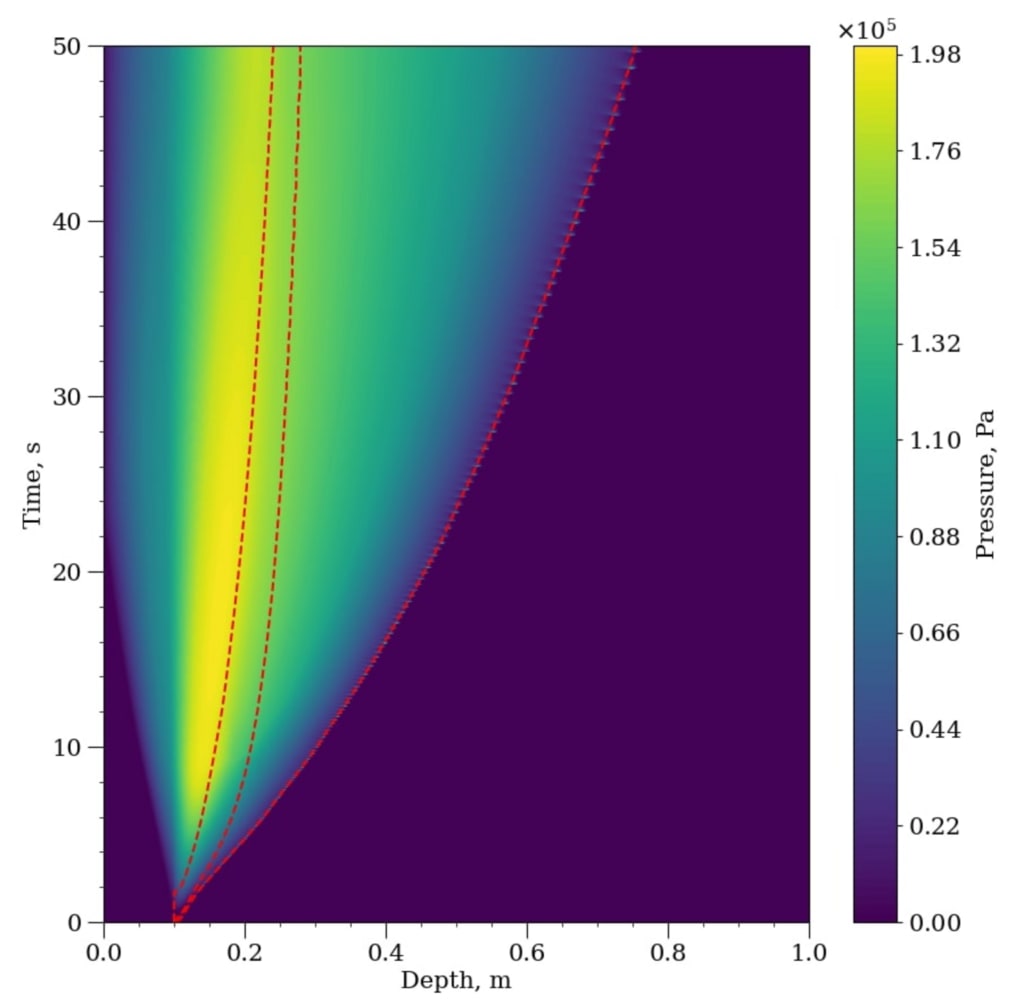
図 2: ラジカルの再結合によって引き起こされる彗星の内部の圧力上昇。 赤い破線の曲線が描かれています (左から右へ)
アモルファスから結晶への転移、OH ラジカルと H ラジカルの再結合フロントの位置。 計算が行われました
最大濃度 1%、表 1 のパラメーター、および ℎ = 0.1 のラジカルの最初の分布 (図 1 を参照) を使用します。
𝜇 = 1、𝑈a,H = 0.03 eV。 ここおよびさらにすべての図において、爆発の時間は H の再結合の開始とともに数えられます。
ラジカル。
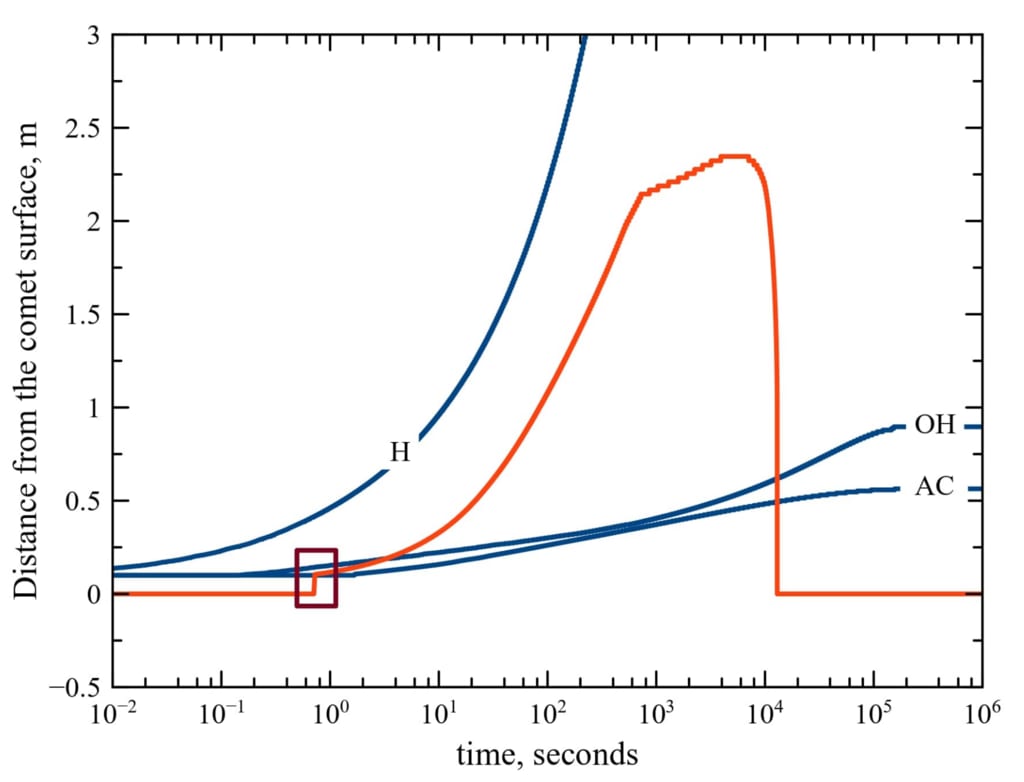
図 3: バースト中の彗星の物理的進化。 アモルファスから結晶への転移 (AC) と OH の位置、
H ラジカルの再結合フロントは青い曲線で示されています。 ガス圧力 > 104 Pa の最深層の位置
赤い曲線で示されています。 紫色の四角は、氷の遷移フロントと一致するガス圧力の初期上昇を示しています。 イニシャル
条件とパラメータは、𝑈a,H = 0.01 eV を除き、図 2 と同じです。
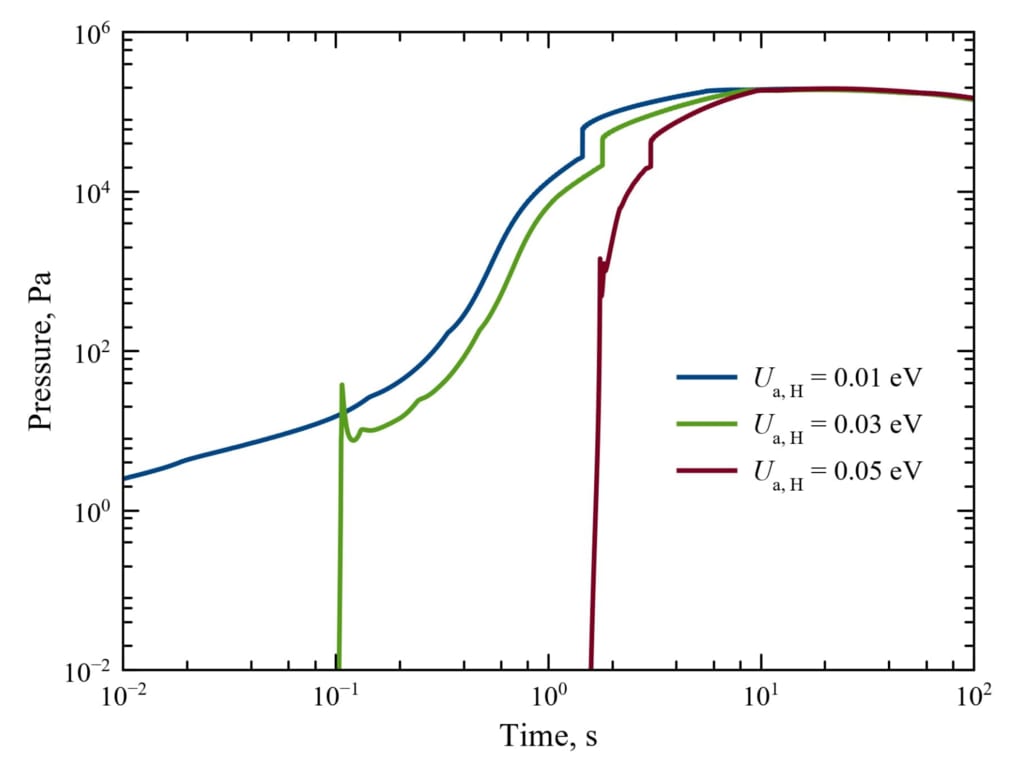
図 4: さまざまな活性化エネルギーに対する時間の関数としての、アモルファスから結晶への氷転移フロントでの圧力上昇
Hラジカルの。 シミュレーションの初期条件とパラメータは図2の通りですが、様々な𝑈a,H。
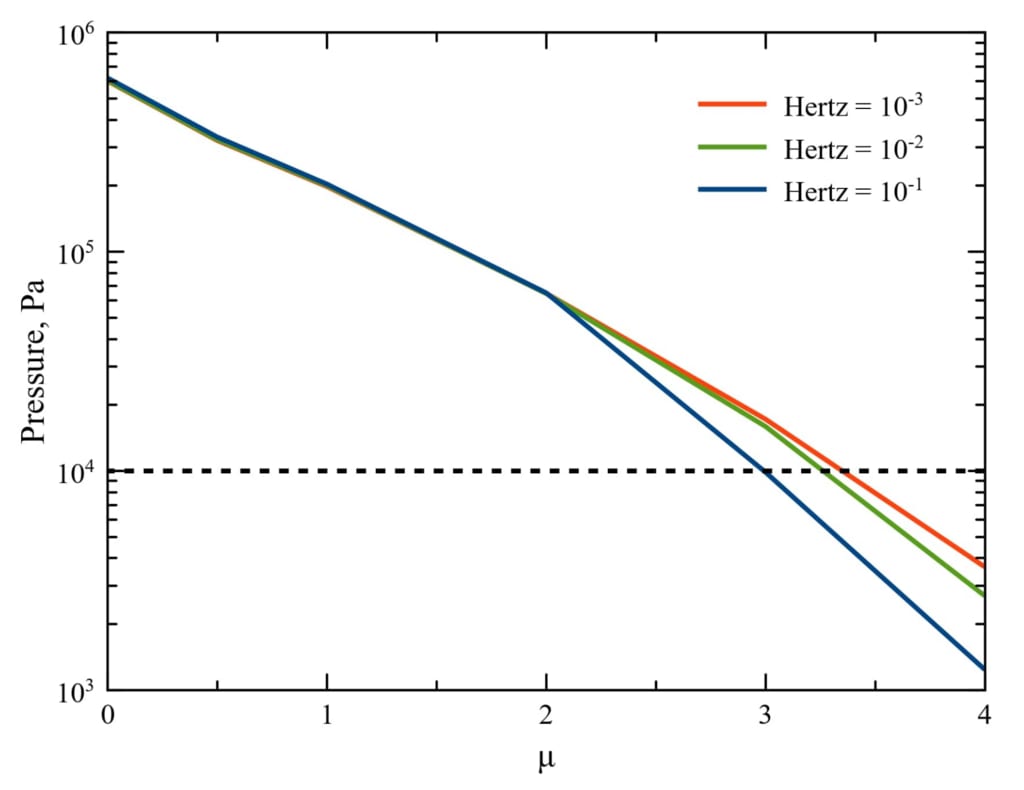
図 5: 3 つの値に対する塵と氷の比 𝜇 に応じた、彗星の表面下に蓄積される最大ガス圧力
ヘルツ係数の。 黒い破線は、コメット材料の引張強度を表します (Reach et al.、2010)。 初期
シミュレーションの条件とパラメータは図2と同じですが、𝑈a,H = 0.01 eV、およびさまざまなℎと𝜇についてです。

図 6: ラジカルの最大濃度の関数として、彗星の表面下に蓄積された最大ガス圧力
氷中 (最初の分布、図 1 を参照)、塵と氷の質量比 𝜇 の 4 つの値について。 黒い破線は張力を表します
彗星の材料の強度 (Reach et al., 2010)。 計算は表 1 のパラメータと ℎ = 0.1、𝑈a,H を使用して実行されました。
= 0.01eV。
4。討議
4. 1. 遠方の彗星の活動源の可能性
私たちは、太陽系の遠方の領域にある彗星の核が再結合によって活動する可能性があることを示しました。
宇宙線照射下で表層に蓄積されるフリーラジカルの量。 可能なパラメータの範囲が広い場合
彗星の物質の組成では、地下空洞内のガス圧力が大規模な引張強度を上回ります。
ガス圧力への主な寄与は、非晶質の氷から放出される CO ガスです。 ガス圧が高いと不安定になる
さらには表面層の完全な拒否を引き起こします。 さらに、非晶質の氷から放出されたガスは両方を流れることができます。
彗星の表面に到達し、より深い層に拡散します(図2、7)。 ラジカルの再結合による局所加熱
効率的なガス拡散を管理し、ガスの瞬間的な凝縮を防ぎます。 この効果により、下層に揮発性物質が豊富に含まれます。 ラジカルの再結合は、観察された活性の考えられる原因の 1 つである可能性があります。
長周期彗星(C/2017 K2 (PANSTARRS)、C/2010 U3 (Boattini)、C/2014 UN271 (Bernardineli-Bernstein))
太陽中心距離が大きい場合。 私たちのモデルは、長周期彗星カイパーの表面活動をシミュレートするために使用できます。
ベルト天体と太陽系外縁天体。 組換え反応が表面で実際に起こっていることを示す重要な指標
太陽系外縁の小天体には H2O2 などの物質が存在するはずです。
とO2
(ジョンソンとクィケンデン、1997)。 ジェームズ・ウェッブ宇宙望遠鏡は、地球の表面上の放射線生成物を検出するために利用できます。
太陽系の外側にある小さな天体。
4.2. モデルの制約
私たちの計算では、ラジカルは彗星物質の氷部分にのみ蓄積できると仮定しています。
ただし、照射中に耐火物(粉塵や有機物)内でラジカルが生成されることもあります。 蓄積
低温での陽子、アルファ、中性子照射下で有機分子内のラジカルの生成を発見
(Carpenter、1987; Kaiser et al.、1997; Shabalin et al.、2003)。 メタン分子内の H 原子の臨界濃度
は 6 ± 3% です (Kaiser et al., 1997)。 一方、ラジカルの蓄積に関する実験結果はありません。
塵の中。 彗星物質中の塵の質量分率は、質量分率に匹敵するか、それを上回る可能性さえあるため、
水の氷、塵の中のラジカルは、彗星の表面のプロセスに大きく寄与する可能性があります。 よく知られているのは、
放射性核種の崩壊は彗星の内層を継続的に照射し、より深い層でラジカルを生成します。
私たちのモデルで考慮されているよりも。 の再結合による化学的および物理的組成の変化が予想されます。
彗星の体積全体に蓄積されたラジカル。 注目すべきは、
ラジカル、臨界濃度と飽和濃度の値は氷のマトリックスに依存します (Johnson と Quickenden、1997)。
彗星の類似体におけるラジカルの蓄積に関する実験結果はありません。 したがって、私たちの計算では、
純氷の実験結果を使用しました。 それにもかかわらず、実験は放射線照射をシミュレートすることが望ましい。
彗星の物質。
観測によると、彗星は化学組成や物理的条件がかなり不均一な天体です。
場所から場所へと変化します。 その結果、彗星は、ラジカルを含む氷が出会うさまざまな領域で活動を経験する可能性があります
連鎖組換え反応が始まる条件。 シミュレーションでは、周囲温度がわずかに上昇しても
再結合フロントの伝播が始まる可能性があるため、表面の加熱を適切にモデル化することが重要です。
すべての表面の不規則性を考慮してください。
私たちのモデルでは、(Gronoff et al., 2020) の GCR の吸収線量を使用しました。 グロノフは次のことを指摘しておく必要があります。
他。 (2020) Badhwar-O’Neill モデルに基づく LIS の計算に使用されます。 で使用される低エネルギー粒子のフラックス
グロノフら。 (2020) は Boschini らと比較して大幅に過大評価されています。 (2020)、GalProp–HelMod を使用した人
モデルとボイジャー 1 号を含むいくつかの機器を使用して LIS を制約します。 新しい LIS は減少すると推定しました
彗星の上部 10 cm のみの線量率。 さらに、GCR スペクトルは太陽系中に変化する可能性があります。
超新星と初期の太陽の活動による進化(Gronoff et al., 2020)。
4.3. 天文学的な意味合い
ラジカルの再結合によって引き起こされる彗星の活動の研究されたメカニズムは、範囲を大幅に拡大します
彗星が活動を経験できる太陽中心距離。 ここで 2 つの非常に重要なアプリケーションを指摘します。
太陽から遠く離れた場所での彗星の活動の様子。
主系列星の周りで検出されたデブリ円盤には、小さな塵や氷の粒子がたくさん含まれています。 の影響
ポインティング・ロバートソンと太陽風の薬剤は、塵粒子の継続的な損失を引き起こします。 一方で、アウトガスは、
彗星核の衝突と微惑星間の衝突により、検出された破片を維持するのに十分な塵粒子が生成される
ディスク (Chen et al.、2008)。 太陽には、太陽系外の破片円盤に比べて塵が比較的少ない円盤があります。 情報源
太陽系外縁領域の惑星間塵粒子のうち、長周期彗星やカイパーベルト天体(ポッペ)ら、2019)。
氷のスパッタリングとポインティング・ロバートソン薬は、氷からの距離が離れるにつれて非効率的になります。
太陽。 その結果、カイパーベルトを越えた領域での遠方の彗星の爆発により、大量の安定した氷が生成される可能性があります。
そして塵の粒子。 太陽の周りのデブリ円盤のモデルは、地球の急激な減少を想定していることを指摘する価値があります。
50 天文単位を超える距離にあるカイパー ベルト天体の数 (Petit et al., 2011)。 おそらくこのカイパーベルトの境界は、
観察の限界によるものです (Fraser et al., 2023)。 この場合、太陽中心の小天体から放出された塵粒子は、
50 天文単位を超える距離は、彗星のような天体の兆候である可能性があります。 私たちの結果によると、彗星の爆発は
太陽系の遠方の領域では、小天体間の相互衝突が重要ではないため、
大量の塵や氷の粒子。 オールトの雲の場合、生成された塵粒子は周期的に発生する可能性があります。
オールトの雲の進化中に太陽系の内部に転送されました。 新しい情報源を探しています
塵粒子は、地球内での未知の起源の異常な拡散光の検出を考慮すると、非常に重要です。
宇宙の銀河系外背景光(Lauer et al., 2022; Carleton et al., 2022)。
彗星の爆発の重要な段階は、彗星に新たに形成された亀裂を通してガスと塵の噴流が噴出することです。
彗星の地殻。 彗星の表面から離れるとき、このジェットは非重力加速度を生み出します (Marsden et al., 1973)。
オールト雲内の彗星核の軌道速度は比較的小さいため、非重力加速度は
よく知られている重力メカニズムに加えて、彗星の軌道を乱すこともあります。 記事(ベロウソフとパブロフ、
2023)、私たちはオールト雲における彗星の軌道の安定性に対する彗星の爆発の影響を調べました。 見せました
半径1km未満の彗星核は、一度の爆発によってオールトの雲から追い出される可能性がある。 これ
この効果は、観察される小半径長周期彗星の数の減少につながる可能性がある(Boe et al., 2019)。
オールトの雲での彗星の爆発
要約
太陽系外縁部の彗星の核には、常に低温の宇宙線が照射されています。
蓄積された高濃度のラジカルは、次の物質と急速に再結合する可能性があります。
彗星の表層が大幅に加熱される。 彗星の活動全体のモデルを提示します
ラジカルの再結合によって生じる太陽中心距離。 検討した結果、
このメカニズムは、たとえ太陽系の遠い領域でも彗星の活動を引き起こす可能性があります。
オールトの雲の距離。 遠く離れた彗星溜まりでの爆発は、新たな塵の発生源となる可能性があります。
宇宙で最近発見された異常な拡散光に寄与する氷の粒子
銀河系外の背景光。 オールトの雲の中の小さな半径の彗星の軌道は次のとおりです。
彗星の爆発の影響を大きく受けています。 この効果は、観察された
小半径の長周期彗星の数。
キーワード: カイパーベルト 彗星 宇宙線 氷
1. はじめに
太陽系の外側には、カイパーベルトとオールトの雲という 2 つの彗星核の発生源があります。 表面
彗星の温度は、カイパーベルトでは 30 ~ 60 K、オールト雲では約 10 K の範囲にあります。 気温が低いため、
彗星が太陽の近くで起こりがちな内部プロセス(水の氷の昇華など)は抑制されます。 いつ
低温における氷の化学的および物理的進化を考慮すると、宇宙線照射は重要な役割を果たします。
氷の性質を変える役割。 カイパーベルトでは、彗星の核に太陽宇宙線(SCR)が照射され、
変調された LIS (局所星間スペクトル) を備えた銀河宇宙線 (GCR)。 カイパーベルトのSCRフラックス
この領域は、太陽系の内部に比べて大幅に減少しています。 オールトの雲の中では銀河宇宙線が
LIS は常に彗星の表面を攻撃します。 高エネルギー粒子の照射によりラジカルやイオンが発生します。
低温の氷。 ラジカルの移動度は温度とともに大幅に低下するため、彗星の核は
太陽系の外側には高濃度のラジカルが蓄積する可能性があります。 実際、氷に陽子を照射する実験では、
電子、中性子、ガンマ光子は、温度 10 ~ 100K の氷中でラジカルが効率的に蓄積することを示しています。
(Moore et al., 1983; Carpenter, 1987; Shabalin et al., 2003; Zhu et al., 2021; Pavlov et al., 2022)。 ラジカルは高い
高温で反応するため、照射された氷の周囲温度がわずかに上昇しただけでも、瞬時に反応が起こる可能性があります。
ラジカルの発熱再結合 (Shabalin et al., 2003)。 また、ラジカル濃度が高いと不安定になります。
自発的組換えに至るまで(Shabalin et al., 2003)。 ラジカルの濃度が1%に達すると、照射された
サンプルはラジカルの再結合により突然発火する可能性があります (Moore および Hudson、1992)。
彗星は太陽に近づくと、太陽の中に放出された塵や氷の粒子に太陽光を反射して明るさを増します。
ハロー。 このプロセスは段階的である場合もあれば、突然である場合もあります。 後者は彗星の爆発と呼ばれます (Gronkowski、2007)。 彗星
爆発は約 3 天文単位の水と氷の昇華境界をはるかに超えて検出されています (Meech et al., 2009)。
非晶質から結晶質への氷の遷移は、からの距離での彗星の爆発の主な原因であると考えられています。
最大14天文単位の太陽。 しかし、最近では、太陽中心距離がはるかに遠い彗星、つまり C/2017 が検出されています。
K2 (PANSTARRS)、C/2010 U3 (Boattini)、および C/2014 UN271 (Bernardineli-Bernstein) は、他の
彗星の活動のメカニズム (Bouziani と Jewitt、2022)。 パブロフらでは、 (2022)、我々は、組み換えが
ラジカルの存在は、太陽中心距離が遠いところで彗星の活動を引き起こす可能性があります。 組換え反応が起こるので、
非常に低い温度では、彗星はオールトの雲の中でも活動を示すことができます。
ここでは、太陽系の遠方領域での彗星の爆発について考えます。 実現可能性を評価するには
太陽中心距離が遠い場所での彗星の活動を考慮して、我々は、彗星爆発によって引き起こされる彗星の爆発のモデルを開発しました。
フリーラジカルの再結合。 モデルについてはセクション 2 で説明します。数値シミュレーションの結果を示します。
セクション 3 で説明し、セクション 4 で説明します。結論はセクション 5 にまとめられています。
2. モデルの説明
2.1. 基本方程式
我々は、Prialnik と Bar-Nun (1987)、Orosei et al. の彗星の内部プロセスを記述するためのモデルを使用します。 (1999) と
マルブフら。 (2012年)。 リストされているすべてのモデルは、太陽中心距離で太陽に接近する彗星用に開発されました。
14AU未満。 照射中、フリーラジカルは彗星の上表層に常に蓄積されるため、
ラジカルを彗星の内部の再生可能なエネルギー源として扱うことができます。 フリーラジカルのまさにこの特徴により、
ラジカルの再結合は、太陽が届くほどの距離にある彗星の内部のプロセスの完璧な持続可能な原動力です。
放射線照射は大幅に減少する(Pavlov et al., 2022)。
私たちのシミュレーションでは、次の彗星の活動モデルを使用します。 ラジカルの再結合により、
層内の塵と氷の温度。 アモルファス氷から結晶氷への転移は約 120 K でゆっくりと始まり、
130 K では急速に進行します (Schmitt et al., 1989)。 アモルファス氷が揮発性ガスの分子を捕捉することはよく知られています。
(例: CO) 低温で (Bar-Nun et al., 1985)。 閉じ込められたガスの放出は、
アモルファスから結晶質への氷の転移。 ラジカルの再結合率が高く、ガス容量が大きいため
非晶質の氷から揮発性物質が放出されると、彗星の表面下に高圧ゾーンが生じる可能性があります。 ガスのとき
圧力が彗星物質の引張強度を超えると、高圧を超えると彗星層が破壊されます。
ゾーンは塵や氷の粒子の噴出によって発生します (Gronkowski および Wesołowski、2015)。
現在のモデルによると、彗星は揮発性ガスが効率的に凝縮して寒冷地で形成された。 の
実験的および理論的研究により、非晶質の氷が彗星の物質の大半を占めていることが示されています。 観測結果から、CO
そしてCO2ガスは彗星の昏睡中に水のほかに最も豊富な成分である。 したがって、私たちのモデルには以下が含まれます
彗星核の 4 つの構成要素: 塵、水氷、CO、CO2。 初期の氷の組成は次によって決まります。
塵と氷の質量比 𝜇 非晶質の氷に閉じ込められたガスの質量分率 𝑓𝑛(𝑛 = CO、CO2) と気孔率 Ψ。
彗星層の質量密度 𝜌 はすべての化合物の合計です。

どこで𝜌d、𝜌a、𝜌c、𝜌𝑛は、塵、非晶質の氷、結晶質の氷、および揮発性物質の質量密度です 𝑛 (c は
氷状態、v は気体状態) をそれぞれ表します。 水蒸気がエネルギーと局所ガス圧力に及ぼす影響
考慮される温度は重要ではありません。
彗星核の熱力学的進化は、全球エネルギー保存方程式に従います。
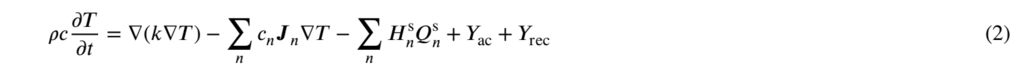
ここで、𝑐 は比熱容量、𝑘 は彗星物質の熱伝導率です。 𝑐 と
𝑘 は Marboeuf et al. に従って計算されます。 (2012年)。 耐火物にはエンスタタイトの比熱容量を利用します。
(ブジアーニとジュイット、2022)。 彗星物質の熱伝導率はヘルツ係数 ℎ に強く影響されます。
(Marboeuf et al.、2012)。 ℎ の一般的な値は 10−1 ~ 10−3 の範囲にあります。
式(2)の項は、 図 1 は、彗星層を通した熱拡散を示しています。 (3) 項は対流を表し、
どこで𝑐
𝑛 と 𝑱𝑛 は、それぞれ揮発性物質 𝑛 の比熱とガス流束です。 (4) 項はエネルギーを説明します。
昇華時の消費と凝縮時のエネルギー放出。ここで 𝑄s 𝑛 はガス源、𝐻𝑛s は潜在ガスです。
𝑛ガス昇華。 (5) 項は、非晶質から結晶質への氷の転移のエネルギーを表します。
閉じ込められたガスの昇華によるエネルギー損失を考慮します。

ここで、𝐻^cr は結晶化の潜熱、𝜆 は結晶化速度です (Schmitt et al., 1989)。 (6)項
ラジカルの再結合中に放出されるエネルギーを説明します。

ここで𝐻^rec 𝑥
𝑥,𝑁𝑥 タイプのラジカル 1 個あたりの再結合反応のエネルギーです。
ラジカルの濃度です
そして𝐾𝑥
組み換え率です。
ラジカルの再結合は、二分子の運動方程式に従います。

アレニウスの法則に従って、𝐾𝑥は温度 𝑇に依存します。

活性化エネルギー 𝑈a,𝑥 とボルツマン定数 𝑘b を使用。
このモデルでは、彗星物質の氷成分に含まれるラジカルのみを考慮し、ラジカルの次の反応を考慮します。

表面境界条件は次のようになります。式のここで、𝐴はボロメトリックボンドアルベド、𝜀は赤外線表面放射率、𝜎はステファン・ボルツマン定数です。

値 𝐹b
彗星核の外部加熱の考えられるすべての原因を説明します。 太陽放射が支配的になるのは、
距離𝑟h
最大10^3AU。 10^3 天文単位(オールトの雲)を超える領域では、宇宙マイクロ波の寄与
背景 (𝐹CMB)、銀河円盤放射 (𝐹disk)、および超新星または通過する明るい O、B 星の放射
(𝐹OB,SN) は (Stern と Shull、1988) を考慮する必要があるため、次のようになります。 2は次のとおりです。

𝐿sはどこですか
太陽の明るさです。
彗星層の組成の変化は、各成分の質量保存方程式を解くことで得られます。
非晶質から結晶質への氷の転移、ガス拡散、昇華/凝縮を考慮した彗星物質の解析:

揮発性物質のガス流量 (𝑛 = CO、CO2) によって与えられます:

どこ𝑃𝑛
は気体 𝑛 と 𝐺𝑛 の分圧です
はガス拡散係数です。 多孔質彗星を通るガスの流れ
物質は、クヌーセン数に応じて、1) 遊離分子 (クヌーセン領域)、2) 粘性、または 3) それらの混合物になります。
このモデルは、ねじれ度 √ を持つ円筒状の細孔を考慮しています。
Marboeufらに続く2件。 (2012年)。
式の表面境界条件は次のようになります。 13 は 𝑃𝑛 = 0 です。結晶氷の昇華は含まれていないため、
考慮された温度では重要ではありません。 粉塵の拡散も考慮していません。
非晶質の氷からの揮発性物質の放出は、局所的な圧力 (𝑃𝑛) がかかると不飽和状態を引き起こします。
)
飽和ガス圧力 𝑃 ^s 𝑛より大きいか小さい。 ガスによる飽和状態の再確立
結露(𝑃𝑛 > 𝑃 sの場合)
𝑛) または氷昇華 (𝑃𝑛 < 𝑃 s の場合)𝑛) よりもはるかに短いタイムスケールで発生します。
アモルファスから結晶質への氷の転移。 モデルは、凝縮/昇華の時間が次の場合に次のように仮定します。
モデルの選択されたタイムステップでは、飽和状態の再確立が瞬時に行われます。 の偏差
飽和圧力からの局所圧力を凝縮ガスの密度に加減算して保証します。
大量保存(Davidsson、2021)。
捕捉されたガスが非晶質の氷から放出されると、ガス圧力が上昇します。 プレッシャーは続く
アモルファス氷からのガス束が彗星を通過する拡散束とのバランスに達するまで増加する
層。 地下領域の圧力の値は、式 1 を使用して計算できます。 2-15. 地下圧力がかかると
彗星物質の引張強度を超えると、亀裂が生じる可能性があります。 この影響により激しい排出が起こる可能性があります
高いガス圧による空洞上の彗星の物質の観察 (Gronkowski と Wesołowski、2015; Prialnik と Sierks、2017)。
ここでは、地下圧力が引張強度を超えたときにバーストが発生すると仮定します。
数値計算では、式 (1) に対して有限体積法による完全陰的スキームを使用します。 1D の 2 と 13
球状の幾何学。 圧力と圧力の変化を制限するために、時間ステップは計算中に常に調整されます。
温度。
2.2. 初期条件とモデルパラメータ
ここでは、オールトの雲にある彗星の核を考えます。 オールトの雲の中の彗星の組成は次のようになりますが、
動的に観測された未知の「新しい」彗星は、オールトの雲にある彗星を表している可能性があります。 モデルは次のことをシミュレートするため、
宇宙線による効果的な照射が起こる彗星の上層の進化、以下にリストされるすべてのパラメータ
表層について説明します。 最初は、揮発性ガス CO と CO2
非晶質の氷の中に閉じ込められた状態でのみ存在します。 私たちは
この制約を使用して、このモデルを、太陽中心距離に基づく大きな彗星の活動のモデルと区別します。
揮発性氷の昇華について。 さらに、凝縮して閉じ込められたガスの昇華も同様の影響を与えます。
彗星の活動の総エネルギー (式 2 を参照)。 CO および CO2 ガスのモル存在量
水に対して
両方とも 10 % (つまり、CO と CO2 の質量比)
水氷まではそれぞれ 0.16 と 0.25)。 これらの値を選択したのは、
𝑓CO と𝑓CO2
理由は 2 つあります: 1) 高濃度でトラップされた揮発性分子により、アモルファスから結晶質が変化します。
氷転移エネルギーはニュートラル。 したがって、このモデルでは、組換え反応が彗星の活動の主なメカニズムとなります。
2) 星間 CO2 のモル存在量
氷は 10 〜 23% の範囲にあり、次の値とほぼ同じです。
CO (Gerakines et al., 1999)。 モデルでは、塵と氷の質量比は、氷が豊富な場合 𝜇 = 0 から氷が少ない場合 𝜇 = 4 まで変化します。
ケース。 Gronkowski and Wesołowski (2015) に従い、細孔半径は 1 𝜇m に設定されています。 強烈なGCR照射により、
彗星の上部層は、有機分子と塵が豊富に含まれた緻密な地殻を生成する可能性があります (Strazzulla と Johnson、1991)。
ここでは、照射によって生成された高密度の地殻が、気孔率の低い耐火物(有機物と塵)で構成されていると仮定します。
Ψ = 0.1、密度は 3000 kg m−3 に近い。 地殻の下では、彗星物質は非常に多孔質であると考えられています (Ψ = 0.65)。
シミュレーションで使用されるすべてのパラメーターを表 1 に示します。 67P/チュリュモフ-ゲラシメンコ ショーの観測結果
彗星は引張強度が数 Pa 程度の低強度天体になる傾向がある (Basilevsky et al., 2016)。 しかし、
長周期彗星の大規模な構造は、短周期彗星のそれとは大きく異なる可能性があります。 加えて、
引張強さは彗星の層の深さに依存する可能性があります。 シミュレーションでは最大推定値を使用します。
Gronkowski と Wesołowski に続く、彗星物質 10^4 Pa の大規模引張強度の研究 (Reach et al., 2010)(2015年)。
フリーラジカルは、1) 周囲温度が上昇したとき (再結合の誘発)、または 2) 次のときに活性化されます。
ラジカルの臨界濃度に達します (自発的再結合)。 モデルは誘発のみを考慮します
組み換え。 活性化エネルギーは
H ラジカルの量 (式 6) は 0.01 eV から 0.11 eV まで変化します (Flournov et al., 1962;Kirichek 他、2017)。
表1
モデルのパラメータ。 パラメータ値
彗星の半径 R、 10^3m
Ψ 0.65
𝑟𝑝、m 10^−6m
ℎ 10^−3−0.1
𝜖 0.96
𝐴 0.04
𝑓𝐶𝑂,𝑓𝐶𝑂2 0.16、0.25
初期温度𝑇0、K 10
ラジカルの初期濃度 𝑁0,𝑥 0 − 1%
𝑈a,H、eV 0.1 − 0.11
𝑈a、OH、eV 0.25
50 K を超える温度では、H ラジカルはヒドロキシルに比べて微量しか存在しません。
ラジカル。 OHラジカルは低温では安定であり、約100Kで活性化エネルギーを持って激しく反応します。
0.25 eV (Johnson および Quickenden、1997; Pavlov et al.、2022)。 ヒドロキシルラジカルの再結合は次の時点から始まります。
したがって、100 K 未満の温度での再結合速度は無視できます。 したがって、我々は考慮しません
私たちのモデルにおけるOHラジカルとHラジカルの相互再結合。 この反応のパラメーターは、次のことからほとんどわかっていません。
実験。 モデルによると、再結合を誘発するには彗星の層を少なくとも 1 ケルビン加熱する必要があります。
Hラジカルの。 式のパラメータ 6 つは (Pavlov et al., 2022) および (Flournov et al., 1962) からのものです。 での長時間照射
気温が低いと、彗星の表層に高い放射線量が蓄積されます。GCR(主に陽子)
彗星の表面から上部 10 メートルにエネルギーを効果的に蓄積します。 グロノフら。 (2020) 照射をモデル化
彗星の質量 (𝜌 = 538 kg m^−3)、𝜇 = 4) を GCR によって計算し、吸収線量プロファイルを取得しました。 彗星の特定の層
臨界値を超えない濃度でラジカルを蓄積することができます。 実験から、自発的に
陽子線が照射された水の氷中での再結合は、H ラジカルの濃度が約 1% (陽子に対して
水の氷の分子の数)(ムーアとハドソン、1992)。 陽子線照射によるHラジカルの発生量を利用
Moore and Hudson (1992) による非晶質氷 7×10^−3 eV−1 と、オールト雲の堆積線量率
(Gronoff et al., 2020)、臨界濃度の蓄積時間は 1 メートルで 10^2 Myr から 10^3 Myr まで変化します。
彗星の表面から10メートルの深さ。 彗星の核の最初の数センチメートルは臨界濃度に達します。
500 万年以内のラジカル。 この効果により、緻密な地殻の形成が促進される可能性があります。
このモデルでは、ラジカル分布の 2 つのプロファイルを使用します。 最初のプロファイルは、最高値が上昇した瞬間に対応します。
ラジカルの集中はダスト層の直下で達成されます。 2 番目のプロファイルは累積に対応します。
表面層のラジカルの平衡飽和濃度の変化(図1)。 Shabalin (1998) によると、飽和した
ラジカルの濃度は、低温での照射線量率に依存しない可能性があります。 その結果、上部は、
彗星の層には、同様の飽和濃度のラジカルが存在する可能性があります。 ここでは、上部 10 メートルのみを仮定します。
彗星の核は、オールト雲の進化中に高濃度のラジカルを蓄積します。
線量沈着率 (Gronoff et al., 2020)。 我々は、上部 10 メートルの初期温度勾配が次のようになることを提案します。
層は重要ではありません。 ラジカルの濃度が臨界濃度 (約 1%) に近いか、それ未満です。
上層10cmはラジカルのないダスト層です。
このモデルはラジカルの誘発再結合を考慮しているため、彗星の表面層は外部からの影響を受ける必要があります。
加熱して組換え反応を引き起こします。 非常に離れた領域 (つまり、オールトの雲) では、
彗星の軌道運動中の太陽放射の変化は重要ではありません。 ただし、近くの超新星や
O/B 星を通過すると、オールト雲内の彗星核が加熱される可能性があります (Stern と Shull、1988)。 スターンとシャル (1988) は示した
太陽の進化の間に、非常に明るい星(クラスOとB)がオールトの雲の近くを通過したこと
系 ≈ 4.5 Byr の結果、少なくとも 1 回の加熱イベントが発生し、各彗星の核の温度が上昇しました。
また、接近超新星により、オールト雲内のすべての彗星が周期的に 30 K まで加熱されます。 ラジカルを持つ層
これを行うには、𝑈a,H = 0.01 eV の場合は少なくとも 1 K 加熱するか、𝑈a,H = 0.11 eV の場合は温度 T = 30 K に達する必要があります。
Hラジカルの再結合を誘発します。

図 1: オールト雲にある彗星のラジカル分布のサンプル。 黒の実線は、
表面ダスト層の下の最大濃度 (1)。 灰色の実線の曲線は、ラジカルが発生したときのラジカルの分布を示しています。
飽和値に達します (2)。 線量沈着率は Gronoff et al. からのものです。 (2020年)。

図 2: ラジカルの再結合によって引き起こされる彗星の内部の圧力上昇。 赤い破線の曲線が描かれています (左から右へ)
アモルファスから結晶への転移、OH ラジカルと H ラジカルの再結合フロントの位置。 計算が行われました
最大濃度 1%、表 1 のパラメーター、および ℎ = 0.1 のラジカルの最初の分布 (図 1 を参照) を使用します。
𝜇 = 1、𝑈a,H = 0.03 eV。 ここおよびさらにすべての図において、爆発の時間は H の再結合の開始とともに数えられます。
ラジカル。

図 3: バースト中の彗星の物理的進化。 アモルファスから結晶への転移 (AC) と OH の位置、
H ラジカルの再結合フロントは青い曲線で示されています。 ガス圧力 > 104 Pa の最深層の位置
赤い曲線で示されています。 紫色の四角は、氷の遷移フロントと一致するガス圧力の初期上昇を示しています。 イニシャル
条件とパラメータは、𝑈a,H = 0.01 eV を除き、図 2 と同じです。

図 4: さまざまな活性化エネルギーに対する時間の関数としての、アモルファスから結晶への氷転移フロントでの圧力上昇
Hラジカルの。 シミュレーションの初期条件とパラメータは図2の通りですが、様々な𝑈a,H。

図 5: 3 つの値に対する塵と氷の比 𝜇 に応じた、彗星の表面下に蓄積される最大ガス圧力
ヘルツ係数の。 黒い破線は、コメット材料の引張強度を表します (Reach et al.、2010)。 初期
シミュレーションの条件とパラメータは図2と同じですが、𝑈a,H = 0.01 eV、およびさまざまなℎと𝜇についてです。

図 6: ラジカルの最大濃度の関数として、彗星の表面下に蓄積された最大ガス圧力
氷中 (最初の分布、図 1 を参照)、塵と氷の質量比 𝜇 の 4 つの値について。 黒い破線は張力を表します
彗星の材料の強度 (Reach et al., 2010)。 計算は表 1 のパラメータと ℎ = 0.1、𝑈a,H を使用して実行されました。
= 0.01eV。
4。討議
4. 1. 遠方の彗星の活動源の可能性
私たちは、太陽系の遠方の領域にある彗星の核が再結合によって活動する可能性があることを示しました。
宇宙線照射下で表層に蓄積されるフリーラジカルの量。 可能なパラメータの範囲が広い場合
彗星の物質の組成では、地下空洞内のガス圧力が大規模な引張強度を上回ります。
ガス圧力への主な寄与は、非晶質の氷から放出される CO ガスです。 ガス圧が高いと不安定になる
さらには表面層の完全な拒否を引き起こします。 さらに、非晶質の氷から放出されたガスは両方を流れることができます。
彗星の表面に到達し、より深い層に拡散します(図2、7)。 ラジカルの再結合による局所加熱
効率的なガス拡散を管理し、ガスの瞬間的な凝縮を防ぎます。 この効果により、下層に揮発性物質が豊富に含まれます。 ラジカルの再結合は、観察された活性の考えられる原因の 1 つである可能性があります。
長周期彗星(C/2017 K2 (PANSTARRS)、C/2010 U3 (Boattini)、C/2014 UN271 (Bernardineli-Bernstein))
太陽中心距離が大きい場合。 私たちのモデルは、長周期彗星カイパーの表面活動をシミュレートするために使用できます。
ベルト天体と太陽系外縁天体。 組換え反応が表面で実際に起こっていることを示す重要な指標
太陽系外縁の小天体には H2O2 などの物質が存在するはずです。
とO2
(ジョンソンとクィケンデン、1997)。 ジェームズ・ウェッブ宇宙望遠鏡は、地球の表面上の放射線生成物を検出するために利用できます。
太陽系の外側にある小さな天体。
4.2. モデルの制約
私たちの計算では、ラジカルは彗星物質の氷部分にのみ蓄積できると仮定しています。
ただし、照射中に耐火物(粉塵や有機物)内でラジカルが生成されることもあります。 蓄積
低温での陽子、アルファ、中性子照射下で有機分子内のラジカルの生成を発見
(Carpenter、1987; Kaiser et al.、1997; Shabalin et al.、2003)。 メタン分子内の H 原子の臨界濃度
は 6 ± 3% です (Kaiser et al., 1997)。 一方、ラジカルの蓄積に関する実験結果はありません。
塵の中。 彗星物質中の塵の質量分率は、質量分率に匹敵するか、それを上回る可能性さえあるため、
水の氷、塵の中のラジカルは、彗星の表面のプロセスに大きく寄与する可能性があります。 よく知られているのは、
放射性核種の崩壊は彗星の内層を継続的に照射し、より深い層でラジカルを生成します。
私たちのモデルで考慮されているよりも。 の再結合による化学的および物理的組成の変化が予想されます。
彗星の体積全体に蓄積されたラジカル。 注目すべきは、
ラジカル、臨界濃度と飽和濃度の値は氷のマトリックスに依存します (Johnson と Quickenden、1997)。
彗星の類似体におけるラジカルの蓄積に関する実験結果はありません。 したがって、私たちの計算では、
純氷の実験結果を使用しました。 それにもかかわらず、実験は放射線照射をシミュレートすることが望ましい。
彗星の物質。
観測によると、彗星は化学組成や物理的条件がかなり不均一な天体です。
場所から場所へと変化します。 その結果、彗星は、ラジカルを含む氷が出会うさまざまな領域で活動を経験する可能性があります
連鎖組換え反応が始まる条件。 シミュレーションでは、周囲温度がわずかに上昇しても
再結合フロントの伝播が始まる可能性があるため、表面の加熱を適切にモデル化することが重要です。
すべての表面の不規則性を考慮してください。
私たちのモデルでは、(Gronoff et al., 2020) の GCR の吸収線量を使用しました。 グロノフは次のことを指摘しておく必要があります。
他。 (2020) Badhwar-O’Neill モデルに基づく LIS の計算に使用されます。 で使用される低エネルギー粒子のフラックス
グロノフら。 (2020) は Boschini らと比較して大幅に過大評価されています。 (2020)、GalProp–HelMod を使用した人
モデルとボイジャー 1 号を含むいくつかの機器を使用して LIS を制約します。 新しい LIS は減少すると推定しました
彗星の上部 10 cm のみの線量率。 さらに、GCR スペクトルは太陽系中に変化する可能性があります。
超新星と初期の太陽の活動による進化(Gronoff et al., 2020)。
4.3. 天文学的な意味合い
ラジカルの再結合によって引き起こされる彗星の活動の研究されたメカニズムは、範囲を大幅に拡大します
彗星が活動を経験できる太陽中心距離。 ここで 2 つの非常に重要なアプリケーションを指摘します。
太陽から遠く離れた場所での彗星の活動の様子。
主系列星の周りで検出されたデブリ円盤には、小さな塵や氷の粒子がたくさん含まれています。 の影響
ポインティング・ロバートソンと太陽風の薬剤は、塵粒子の継続的な損失を引き起こします。 一方で、アウトガスは、
彗星核の衝突と微惑星間の衝突により、検出された破片を維持するのに十分な塵粒子が生成される
ディスク (Chen et al.、2008)。 太陽には、太陽系外の破片円盤に比べて塵が比較的少ない円盤があります。 情報源
太陽系外縁領域の惑星間塵粒子のうち、長周期彗星やカイパーベルト天体(ポッペ)ら、2019)。
氷のスパッタリングとポインティング・ロバートソン薬は、氷からの距離が離れるにつれて非効率的になります。
太陽。 その結果、カイパーベルトを越えた領域での遠方の彗星の爆発により、大量の安定した氷が生成される可能性があります。
そして塵の粒子。 太陽の周りのデブリ円盤のモデルは、地球の急激な減少を想定していることを指摘する価値があります。
50 天文単位を超える距離にあるカイパー ベルト天体の数 (Petit et al., 2011)。 おそらくこのカイパーベルトの境界は、
観察の限界によるものです (Fraser et al., 2023)。 この場合、太陽中心の小天体から放出された塵粒子は、
50 天文単位を超える距離は、彗星のような天体の兆候である可能性があります。 私たちの結果によると、彗星の爆発は
太陽系の遠方の領域では、小天体間の相互衝突が重要ではないため、
大量の塵や氷の粒子。 オールトの雲の場合、生成された塵粒子は周期的に発生する可能性があります。
オールトの雲の進化中に太陽系の内部に転送されました。 新しい情報源を探しています
塵粒子は、地球内での未知の起源の異常な拡散光の検出を考慮すると、非常に重要です。
宇宙の銀河系外背景光(Lauer et al., 2022; Carleton et al., 2022)。
彗星の爆発の重要な段階は、彗星に新たに形成された亀裂を通してガスと塵の噴流が噴出することです。
彗星の地殻。 彗星の表面から離れるとき、このジェットは非重力加速度を生み出します (Marsden et al., 1973)。
オールト雲内の彗星核の軌道速度は比較的小さいため、非重力加速度は
よく知られている重力メカニズムに加えて、彗星の軌道を乱すこともあります。 記事(ベロウソフとパブロフ、
2023)、私たちはオールト雲における彗星の軌道の安定性に対する彗星の爆発の影響を調べました。 見せました
半径1km未満の彗星核は、一度の爆発によってオールトの雲から追い出される可能性がある。 これ
この効果は、観察される小半径長周期彗星の数の減少につながる可能性がある(Boe et al., 2019)。
5。結論
私たちは、太陽中心距離が遠いところでの彗星の再結合によって引き起こされる彗星の活動モデルを開発しました。
低温での宇宙線照射により蓄積されるラジカル。 主な結論は次のとおりです。
• 私たちのモデルは、ラジカルの再結合が太陽中心の大きな領域で彗星の爆発を引き起こす可能性があることを示しています。
観測されたものと同様の総放出質量を持つオールト雲の中でも彗星の活動を距離を保ち、予測します。
暴発。
• 再結合反応は、彗星物質に重大な化学変化を引き起こす可能性があります。
• カイパーベルトを越えた大量の塵や氷の粒子の放出が、最近の地球温暖化の原因となっている可能性がある。
原因不明の異常な拡散光を発見。
• オールト雲での彗星の爆発は、観測される小半径の長周期彗星の数の減少につながる可能性がある
私たちは、太陽中心距離が遠いところでの彗星の再結合によって引き起こされる彗星の活動モデルを開発しました。
低温での宇宙線照射により蓄積されるラジカル。 主な結論は次のとおりです。
• 私たちのモデルは、ラジカルの再結合が太陽中心の大きな領域で彗星の爆発を引き起こす可能性があることを示しています。
観測されたものと同様の総放出質量を持つオールト雲の中でも彗星の活動を距離を保ち、予測します。
暴発。
• 再結合反応は、彗星物質に重大な化学変化を引き起こす可能性があります。
• カイパーベルトを越えた大量の塵や氷の粒子の放出が、最近の地球温暖化の原因となっている可能性がある。
原因不明の異常な拡散光を発見。
• オールト雲での彗星の爆発は、観測される小半径の長周期彗星の数の減少につながる可能性がある




















※コメント投稿者のブログIDはブログ作成者のみに通知されます