オウムアムアの光度曲線のモデリング：トルクと円板状形状の証拠

オウムアムアは光度曲線的に円盤状か葉巻か断定できない？と思ったら円盤状。以下、機械翻訳。
オウムアムアの光度曲線のモデリング：トルクと円板状形状の証拠
（2019年6月9日に提出された）
任意のトルクを含む物理モデルを使って、星間訪問者のオウムアムアの光度曲線にフィットする最初の試みを提示します。従来型（Lommel-Seeliger 3軸楕円体）と代替型（ "白黒ボール"、 "ソーラーセイル"）の両方の明るさモデルを検討します。すべての明るさモデルで、小惑星の光度曲線の最も顕著な特徴 - 極小値 - のタイミングを説明するためにいくらかのトルクが必要です。私達の最もよく合うモデルは軸対称であることに非常に近い薄いディスク（アスペクト比1：6）と薄い葉巻（アスペクト比1：8）です。どちらのモデルも転動しており、ダイナミクスがガス放出によって影響を受ける太陽系彗星のように、オウムアムアの線形非重力加速度に対して同じ振幅を持つトルクを必要とします。角運動量ベクトルのランダムな向きを仮定して、我々は我々の最良適合モデルの確率を計算する。葉巻型のモデルは微調整の問題を抱えており、 オウムアムアの光度曲線に存在するものと同じくらいの深さで光度曲線の最小値を生成する確率が16％しかないことを示します。一方、ディスク型モデルは、必要な深さを最小限に抑える可能性が非常に高い（91％）。私たちの分析によると、 `オウムアムアの最も可能性の高いモデルは、ガス放出から適度なトルクを受けている薄いディスク（スラブ）です。一方、必要とされる深さの最小値を生み出す可能性は非常に高い（91パーセント）。
図1.慣性座標系からの変換
XY Z（Zは角運動量の初期方向）ベクトルL）をオイラーを使用して移動座標系bcaに変換　角度θ、φ、およびψ。


図2人工データセットテスト tはそれ以降の日数
MJD = 58050、Vはrスペクトルの絶対値　フィルタ。 1シグマエラーバーを含む人工データポイントが表示されます
緑色（ジャーナルの印刷版では灰色）。 黒い線　基礎となるモデルの光度曲線を示します。 オレンジ（グレー
ジャーナル行の印刷版は、最も適合するモデルに対応します。


図3.当社の最も適したタンブリング小惑星モデル
（TD60B、小惑星2002年TD 60の表1）。 tはそれ以降の日数MJD = 52500、VはRスペクトルフィルターの絶対値です。 ドットはPravec et al。からの993の観測データポイントです。
（2005）。 上部パネルと下部パネルはパネル（c）に対応しています　（d）Pravec et al。の図4の。 （2005）。



図4.オウムアムアで観測された光度曲線（770ポイント）
Fraserらのデータセットに基づいています。 （2018年、黒点）そしてDrahusら。 （2018年、赤い点、印刷されたバージョンの灰色の点
ジャーナルの）。 tはMJD = 58050からの日数、Vはr / rの絶対値　スペクトルフィルタ エラーバー　1シグマの不確実性です。


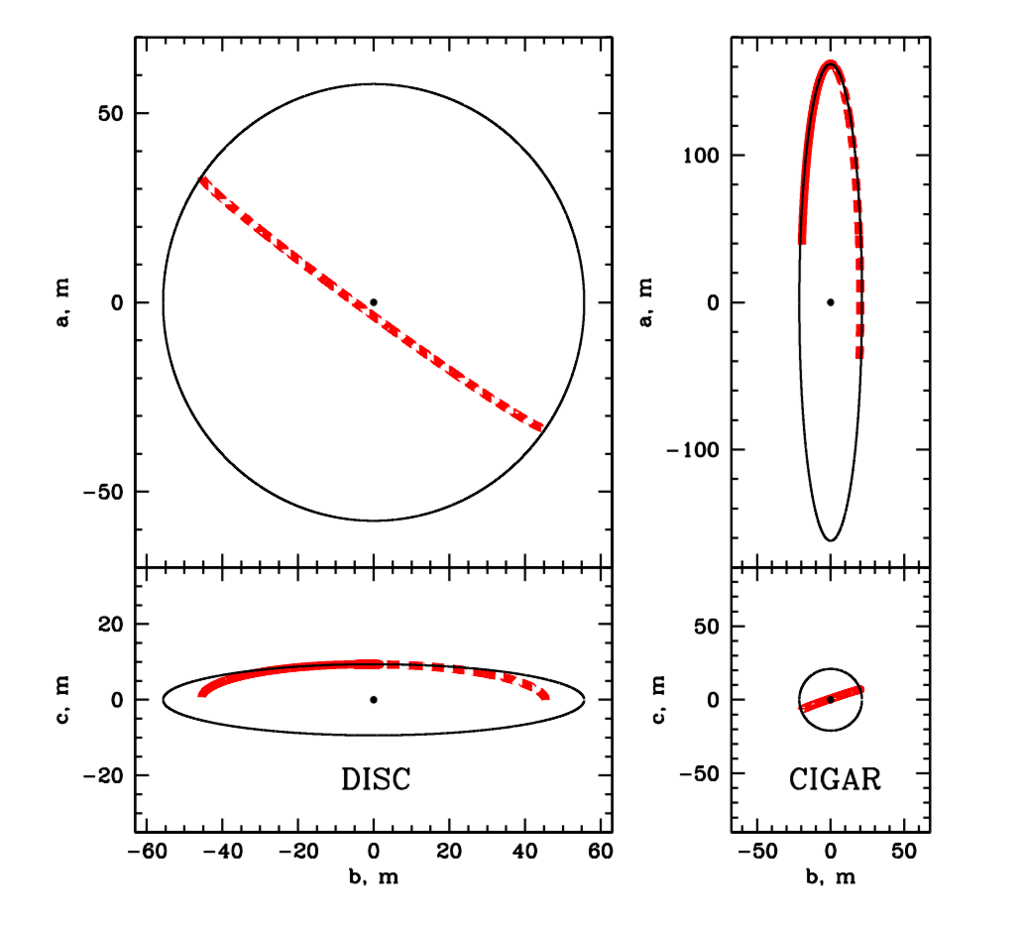
図8. 2つのモデルの投影 - DISC（左パネル）とCIGAR（右パネル） - bOa（上）とbOc（下）の平面へ。
細い黒い線は小惑星の範囲を示しています。 濃い赤（グレー）ジャーナルの印刷版では行は可能に対応します
ガス放出点の位置。 （目に見えない - 小惑星の体の後ろにある部分は破線で表示されています。）点が表示されます
小惑星の中心。 幾何学的アルベドp = 0.1としました。