散乱円盤天体 (SDO)の中で遠日点が異様に遠い天体は、天の川銀河の力と星団内部での接近遭遇で説明できる。説です。以下、機械翻訳。
遠方の海王星太陽系天体の放射状分布が示す点 星団における太陽の形成
概要
散乱円盤天体 (SDO) は、長半径 50 < a ≲ 1000 au、近日点距離 q ≳ 30 au を持つ海王星以遠天体の集団です。
海王星が届かない軌道を持つ切り離された SDO (およそ q > 35 天文単位)
ここでは、初期の進化に対する重要な制約として特に興味深いものです。
太陽系の外側。 50 ~ 500 au での分離された SDO の長半径プロファイル、
Dark Energy Survey (DES) から特徴付けられるように、放射状に広がっていますが、
海王星の初期移行に関する以前の動的モデルは、相対的にコンパクトなプロファイル。 この問題はおそらく太陽の誕生環境に関係している
星団の中で。 を考慮した新しい動的シミュレーションを実行します。
クラスター効果を解明し、SDO の軌道分布を説明できることを示す
特に近い恒星との遭遇が早い段階で起こった場合(例:M 矮星と質量≃ 0.2 M⊙ ≃ 200 au で太陽に接近します。 そんな出会いのために
かなり高い確率で起こり、太陽は恒星の中で形成されたに違いない
ηT ≳ 10^4 Myr pc^−3 のクラスター、ここで、η は星の数密度、T は太陽が星団内に存在する時間。
1. はじめに
カイパーベルトの力学的構造は、その形成とその形成に関する手がかりとして使用できます。
太陽系、惑星系全般、そして特に海王星の初期の軌道の進化。 海王星の軌道移動の正確な性質は、研究の主題となっている。
かなりの研究(最近の研究については、Morbidelli & Nesvorn´y 2020 および Gladman & Volk 2021 を参照)
レビュー)。 この問題は、さまざまな初期条件と海王星の軌道進化をテストし、モデルの予測を比較するフォワード モデリングによって最もよく解決されます。
観察に。 初期の研究では、海王星が初期移行中の現在の eN ≃ 0.01 に匹敵する非常に低い軌道離心率
(例、Malhotra 1993、1995; Gomes 2003; Hahn & Malhotra 2005)。 後に、外惑星のやや励起された軌道を説明するために、巨大惑星の不安定性モデルが提案されました。
(Tsiganis et al. 2005)。 元の不安定モデルでは、海王星は高度に分散していました。
カイパーベルトと一時的に重なった離心軌道 (eN ≳ 0.2) (Levison et al. 2008)。
特定の移民/不安定体制を排除するために、さまざまな議論が展開されている
(例、Batygin et al. 2011; Dawson & Murray-Clay 2012)。 たとえば、高偏心率
海王星の軌道の急速な(e 倍 τ 〜 1 Myr)環状化を伴う不安定モデルは、カイパー ベルト天体 (KBO) の幅広い傾斜分布を再現します。
このモデルでは軌道を動的に励起するのに十分な時間がありません (Volk & Malhotra 2011、Nesvorn´y)
2015a)。 海王星の離心率が非常に低い移行モデル (eN ≲ 0.03; Volk &Malhotra 2019) 50 < a < 60 au、近日点距離 q > 35 au の KBO は説明されていません。
そして i < 10°(ネスヴォルニー 2021)。 したがって、最新の研究のほとんどは、
eN ≃ 0.03–0.1 および τ ∼ 10 Myr の不安定性 (Nesvorn´y & Morbidelli 2012; Kaib &
シェパード 2016; デイエンノら。 2017年、2018年。 ローラーら。 2019年; クレメントら。 2021)。
前の研究では、共振と動的のための動的モデルを開発しました。
ホット KBO (Nesvorn´y & Vokrouhlick´y 2016)、動的コールド KBO (Nesvorn´y 2015b)、
SDO (Kaib & Sheppard 2016、Nesvorn´y et al. 2016)。 これらのモデルの最新のものは、
外部太陽系起源調査 (OSSOS; Bannister et al. 2018) によって制約される
観察 (Nesvorn´y et al. 2020)。 たとえば、図 1 は成功したダイナミクスを比較しています。
海王星が低離心率で移動したと仮定したモデルを使用したシミュレーション
軌道 (eN ≃ 0.01)。 結果は、海王星の移動は長距離 (≲ 25au から 30 au)、ゆっくり (τ ≳ 10 Myr) で、粒子が粗かった (冥王星サイズの天体との散乱遭遇のため) ことを示しています。
天体)、そして海王星が到達したとき、海王星の離心率は eN ≃ 0.03–0.1 まで励起されたと考えられます。
≃ 28 天文単位 (おそらく惑星クラスの天体との遭遇によるもの)。
ここでは SDO について考えます。 SDO は、散在する集団と孤立した集団に分類できます。
グラッドマンら。 (2008) は、散乱 SDO を動的に結合されるオブジェクトとして定義しました。
海王星 (1000 万の長い積分ウィンドウで長半径変化 ∆a > 1.5 au、プラス
a > 47.8 au)、分離された SDO は結合されていないものとして (非共振、Δa < 1.5)
au、および古典的な KBO を避けるために e > 0.24)。 ここでは、より単純な定義を採用します。 私たちは避けます
の形成に関する議論を混同したくないため、< 60 au の軌道を使用します。
遠隔/分離したSDOと、強い5:2共鳴への物体の捕捉に関連するSDO ≃ 55.5 au (Gladman et al. 2012)。 60 < a < 500 au のオブジェクトは次のように分離されます。
近日点距離 q = a(1−e) < 35 au (散乱 SDO) および q > 35 au のもの
(分離された SDO)。 Gladman らの定義とよく一致します。 (2008)
q < 35 au の SDO は通常海王星によって散乱されるのに対し、q > 35 の SDO は海王星によって散乱されるためです。
auは違います。 重要なのは、同じ(私たちの)定義をモデルと観測されたものの両方に適用することです。
人口 - これにより、2 つを正確に比較できるようになります。
この取り組みにおける私たちの当面の目的は、孤立した人々の長年の問題を解決することです。
SDO。 この問題は図 2 に示されており、偏ったモデルは放射状プロファイルを示しています。
観測よりも大きな軌道半径では分離した SDO がはるかに少なくなります。1 何かが明らかにあります。
ここを離れてください。 放射状プロファイルの問題は、これまでにテストしたすべての移行モデルに存在します。
具体的には、次の条件でモデルをテストしました。 (1) 海王星の移動のさまざまなタイムスケール (τ = 5、(10、30、100 Myr)、
(2) 海王星の離心率の異なる励起 (e.g.、eN = 0、0.03および 0.1)、
(3) 海王星の離心率の異なる減衰タイムスケール (e 倍 τe = 5、10、30)
(4) 元の微惑星円盤の異なる半径方向プロファイル (Nesvorn´y etアル。 2020)、および(5)不安定時の海王星のジャンプの有無。
問題
銀河ポテンシャル/星がモデルに含まれているかどうかとは無関係に存続します (Nesvorn´y et al. 2017)。 さらに、この問題は当初、
このモデルは太陽系外縁起源調査 (OSSOS) の検出結果と比較されました。
Dark Energy Survey (DES) の観測結果と比較すると、さらに明らかです。
SDO (Bernardinelli et al. 2022) (図 2)。
私たちは現在、この問題に対する興味深い解決策を見つけたと信じています。 それをテストするために、私たちは
Adams は、星団を使用して新しいシミュレーションを実行しました (Adams 2010)。 クラスターの可能性と
星団星との遭遇は、Batygin et al. に記載されている方法に従ってモデル化されました。
(2020) (セクション 2)。 他のすべての側面では、力学モデルは同じままでした。 議論していくうちに
昆虫。 図3に示すように、新しいモデルは、50 天文単位未満で KBO の同じ軌道分布を生成しました。
ただし、50 au を超える場合、分離された SDO のモデル母集団はより放射状に広がります。
クラスター効果を考慮した場合。 さらに、特に次のように仮定すると、
恒星接近は早い段階で発生しており、モデルは放射状と正確に一致することができます。
DES によって検出された分離した SDO のプロファイル (Bernardinelli et al. 2022; Section 3)。
恒星クラスター効果は、極端な KBO を説明するために以前に援用されました (Kenyon と
ブロムリー 2004; モルビデリ&レヴィソン 2004; ブラッサーら。 2006年、2012年。 ブラッサー&シュワンブ
2015)、(90377) Sedna および 2012 VP113 (a > 200 au、q ≃ 75–80 au; Brown et al.
2004、トルヒーヨ&シェパード 2014)。 結果は、太陽が星団の中で誕生したことを示しています
N 〜 10^3 以上の星があり、太陽が少なくとも T 〜 10 の間星団内に留まったこと
ミル。 ただし、極端な KBO は少数しか知られていないため、これらの結果は小さな影響を受ける可能性があります。
数値統計。 さらに、極端な KBO はさまざまな観測で検出されました。
異なる検索戦略を採用し、異なる限界値を持ったプログラム。 それ
したがって、その検出に関与する強いバイアスをどのようにモデル化するかは明らかではありません。 あれは
35 < q < 50 au の分離された SDO の放射状構造はなぜよく特徴付けられているのか
DES 観測 (> 50 au で検出された ≃ 200 個の KBO) から、有用な情報を表すことができます。
クラスターのプロパティに対する制約。
6. 結論
私たちは、切り離された SDO の放射状分布に関する長年の問題を指摘しました。
そして、太陽が特に接近した場合、この問題は解決できることを示しました。
星団星 (例: 質量 ≃ 0.2 M⊙、最小距離 ≲ 200 の M 矮星)
オー)。 このような接近遭遇により、フェルナンデス雲オブジェクトの大規模な集団が形成され、
この集団は a < 200 au および q < 50 au まで広がり、放射状構造に影響を与えます。
ダークエネルギー調査によって検出された分離した SDO の数 (Bernardinelli et al. 2022)。 私たちは
この効果を詳細に文書化するために 3 つの新しいシミュレーションを実行しました。 軌道分布
さまざまなモデルで取得された分離された SDO の一部は、DES シミュレーターでバイアスされ、
観測結果と 1 対 1 で比較します。 同じ方法を以下にも適用しました
十数の以前のモデルは、特性に関する仮定が異なりました。
海王星の移動ですが、星団の影響は含まれておらず、海王星の移動の影響に関連する多くの可能性を排除できることを示しています。
ディスク の散乱体の放射状構造における惑星9または浮遊惑星の影響の調査は将来の作業のために残されています。
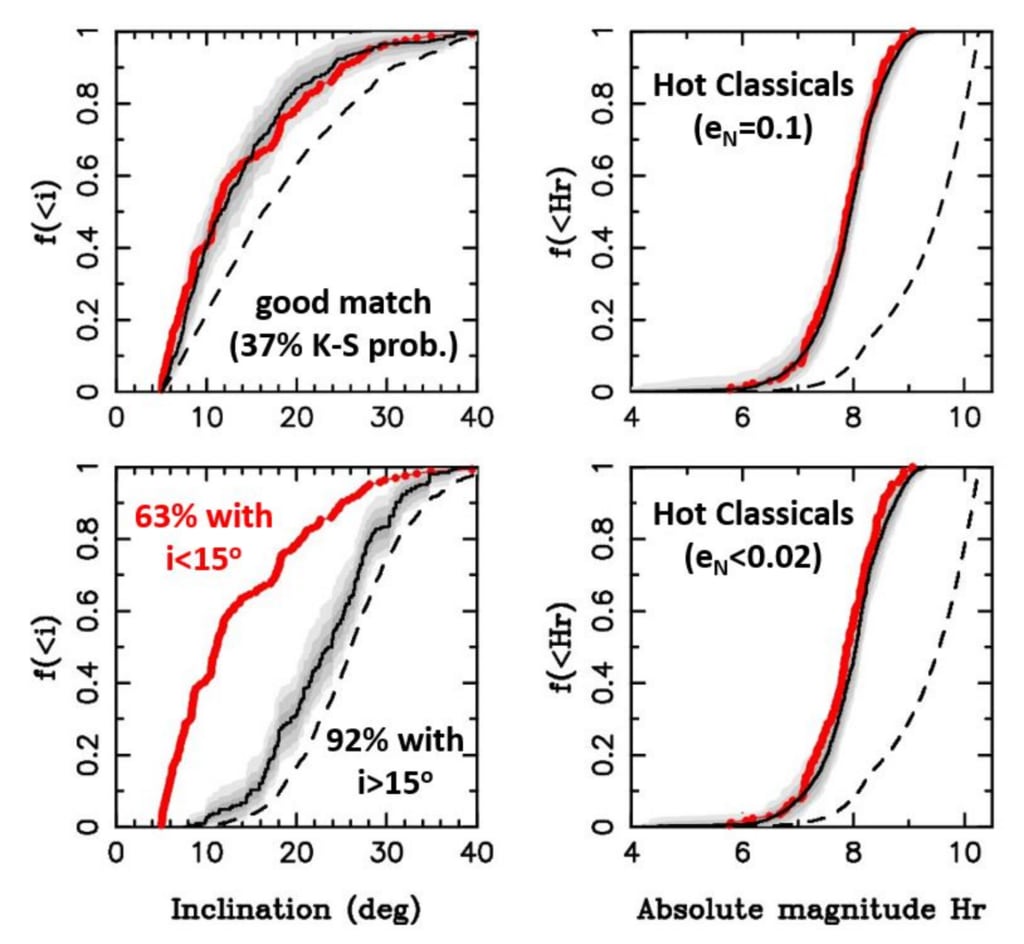
図 1.— 偏りのあるモデル (黒線) と OSSOS 観察の比較
ホット クラシックの (赤い点) (40 < a < 47 au、q > 36 au、i > 5)
◦; ネスヴォルニーら。 2020年)。 の
固有モデルの分布は破線で示されています。 斜線部分は 1σ (太字グレー)、
2σ (中) および 3σ (ライトグレー) エンベロープ。 モデルの結果を使用して、10,000 個のデータを生成しました。
それぞれ 164 体からなるランダム サンプル (サンプル サイズは OSSOS の数と同じ)
検出)。 サンプルには OSSOS シミュレーターを使用してバイアスをかけました (Lawler et al. 2018)。
サンプルの 68.3% (1σ)、95.5% (2σ)、および 99.7% (3σ) を含むエンベロープを特定しました。
それらをここにプロットしました。 下のパネルは、低偏心移動を備えたモデルを示しています。
海王星の値 (eN ≃ 0.01)。 この場合、軌道は香西によって海王星から切り離されます。
共鳴 (Kozai 1962) により、軌道が非常に少ない特定の傾斜分布が作成されます。
15°未満
(ネスヴォルニー 2021)。 上のパネルは、Neptune の成功モデルを示しています。
海王星が ≃ 28 au に達したとき、離心率は eN = 0.1 まで励起され、ゆっくりと減衰しました。
その後。 K-S テストは、成功者と成功者からの傾斜分布に適用されました。
(偏った) モデルでは、失敗したケースの確率はそれぞれ 37% と 10−10 未満です。
そして、観察された分布は、同じ基礎となる分布から抽出されます。 適合図
Nesvorn´yらより。 (2020年)。

図 2.— 切り離された SDO の問題。 プロットは、偏ったデータ間の比較を示しています。
銀河シミュレーションとダーク エネルギー サーベイ (DES) 観測からのモデル (黒線)
切り離された SDO の (赤線)。 セクションを参照してください。 2 モデルパラメータと DES の説明
(Bernardinelli 他、2022)。 固有モデルの分布は破線で示されています。 見る
斜線部分の意味については、図 1 のキャプションを参照してください。 コルモゴロフ・スミルノフ (K-S) 検定
長半径分布 (パネル a) に適用すると、
偏りのあるモデルと観察された分布は、同じ基礎となる分布から抽出されます。
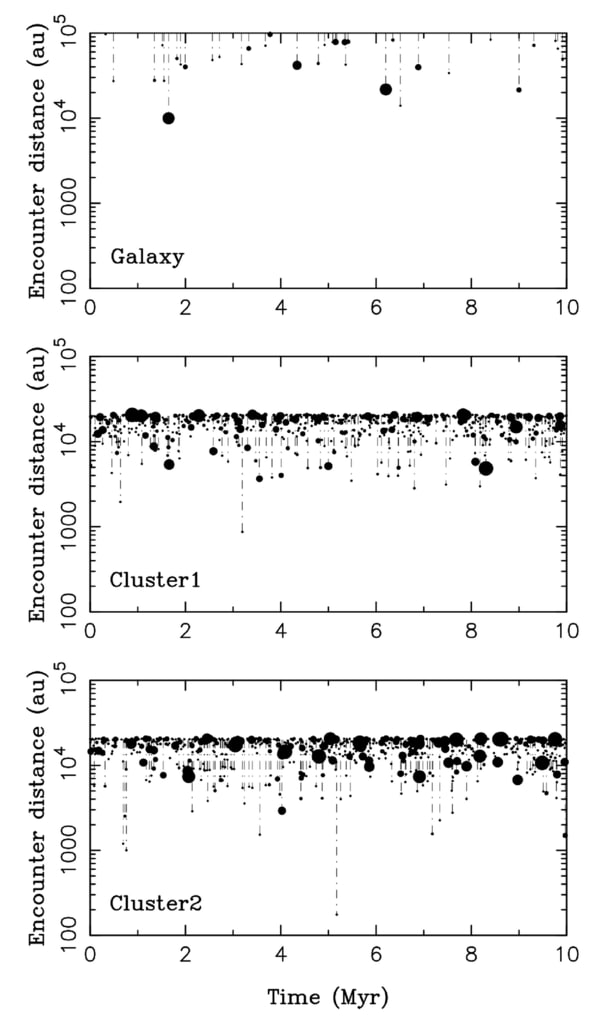
図 3. 最初の 1000 万年後の恒星との遭遇。 パネルは上から下に表示されます。
この研究で考慮される 3 つのケースでの遭遇: (1) 星団なし、太陽との遭遇
銀河内の恒星 (銀河というラベルが付けられている)、(2) 比較的遠くにある恒星と遭遇する星団
(クラスター 1)、(3) 比較的近い恒星に遭遇したクラスター (クラスター 2)。 サイズ
シンボルは星の質量と相関します。 Cluster2 の最接近遭遇は次のとおりです。
0.17 M⊙ の星が最小距離 d ≃ 175 au で通過するとき、t ≃ 5.17 Myr。 効果
この遭遇について、KBO の傾斜分布と惑星軌道について議論します。
セクション 4 で。
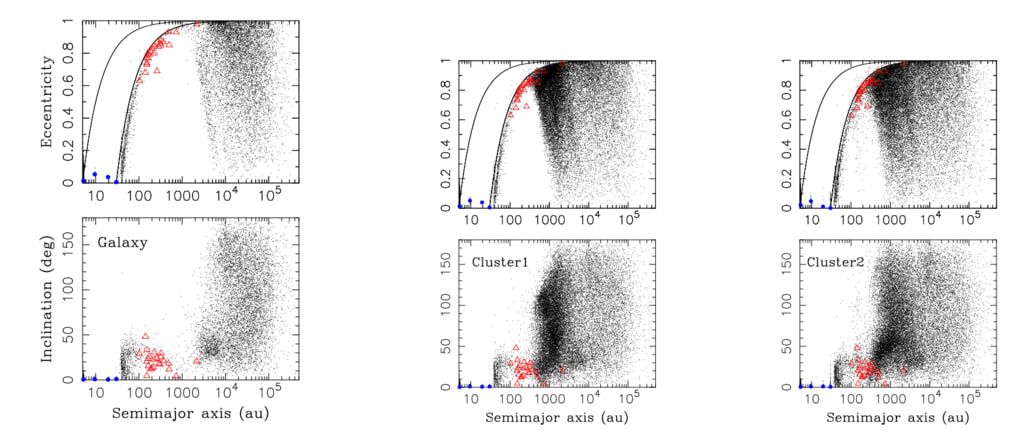
図 4.— 3 つのモデルからの物体の軌道分布: (1) クラスターなし (ラベル付き)
(2) 比較的遠くに星が出現した星団 (Cluster1)、(3) 星団
比較的近い恒星との遭遇が見られます (クラスター 2)。 すべてのシミュレーションには銀河潮汐が含まれています
そして太陽と銀河の星との出会い。 モデル母集団をサブサンプリングしました。
ここでは、シミュレーション時刻 t = 4.6 Gyr (現在の時代) を、制限するために 4 倍して示しています。
飽和。 赤い三角形は、既知の極端な KBO の軌道を示しています。
遠方の海王星太陽系天体の放射状分布が示す点 星団における太陽の形成
概要
散乱円盤天体 (SDO) は、長半径 50 < a ≲ 1000 au、近日点距離 q ≳ 30 au を持つ海王星以遠天体の集団です。
海王星が届かない軌道を持つ切り離された SDO (およそ q > 35 天文単位)
ここでは、初期の進化に対する重要な制約として特に興味深いものです。
太陽系の外側。 50 ~ 500 au での分離された SDO の長半径プロファイル、
Dark Energy Survey (DES) から特徴付けられるように、放射状に広がっていますが、
海王星の初期移行に関する以前の動的モデルは、相対的にコンパクトなプロファイル。 この問題はおそらく太陽の誕生環境に関係している
星団の中で。 を考慮した新しい動的シミュレーションを実行します。
クラスター効果を解明し、SDO の軌道分布を説明できることを示す
特に近い恒星との遭遇が早い段階で起こった場合(例:M 矮星と質量≃ 0.2 M⊙ ≃ 200 au で太陽に接近します。 そんな出会いのために
かなり高い確率で起こり、太陽は恒星の中で形成されたに違いない
ηT ≳ 10^4 Myr pc^−3 のクラスター、ここで、η は星の数密度、T は太陽が星団内に存在する時間。
1. はじめに
カイパーベルトの力学的構造は、その形成とその形成に関する手がかりとして使用できます。
太陽系、惑星系全般、そして特に海王星の初期の軌道の進化。 海王星の軌道移動の正確な性質は、研究の主題となっている。
かなりの研究(最近の研究については、Morbidelli & Nesvorn´y 2020 および Gladman & Volk 2021 を参照)
レビュー)。 この問題は、さまざまな初期条件と海王星の軌道進化をテストし、モデルの予測を比較するフォワード モデリングによって最もよく解決されます。
観察に。 初期の研究では、海王星が初期移行中の現在の eN ≃ 0.01 に匹敵する非常に低い軌道離心率
(例、Malhotra 1993、1995; Gomes 2003; Hahn & Malhotra 2005)。 後に、外惑星のやや励起された軌道を説明するために、巨大惑星の不安定性モデルが提案されました。
(Tsiganis et al. 2005)。 元の不安定モデルでは、海王星は高度に分散していました。
カイパーベルトと一時的に重なった離心軌道 (eN ≳ 0.2) (Levison et al. 2008)。
特定の移民/不安定体制を排除するために、さまざまな議論が展開されている
(例、Batygin et al. 2011; Dawson & Murray-Clay 2012)。 たとえば、高偏心率
海王星の軌道の急速な(e 倍 τ 〜 1 Myr)環状化を伴う不安定モデルは、カイパー ベルト天体 (KBO) の幅広い傾斜分布を再現します。
このモデルでは軌道を動的に励起するのに十分な時間がありません (Volk & Malhotra 2011、Nesvorn´y)
2015a)。 海王星の離心率が非常に低い移行モデル (eN ≲ 0.03; Volk &Malhotra 2019) 50 < a < 60 au、近日点距離 q > 35 au の KBO は説明されていません。
そして i < 10°(ネスヴォルニー 2021)。 したがって、最新の研究のほとんどは、
eN ≃ 0.03–0.1 および τ ∼ 10 Myr の不安定性 (Nesvorn´y & Morbidelli 2012; Kaib &
シェパード 2016; デイエンノら。 2017年、2018年。 ローラーら。 2019年; クレメントら。 2021)。
前の研究では、共振と動的のための動的モデルを開発しました。
ホット KBO (Nesvorn´y & Vokrouhlick´y 2016)、動的コールド KBO (Nesvorn´y 2015b)、
SDO (Kaib & Sheppard 2016、Nesvorn´y et al. 2016)。 これらのモデルの最新のものは、
外部太陽系起源調査 (OSSOS; Bannister et al. 2018) によって制約される
観察 (Nesvorn´y et al. 2020)。 たとえば、図 1 は成功したダイナミクスを比較しています。
海王星が低離心率で移動したと仮定したモデルを使用したシミュレーション
軌道 (eN ≃ 0.01)。 結果は、海王星の移動は長距離 (≲ 25au から 30 au)、ゆっくり (τ ≳ 10 Myr) で、粒子が粗かった (冥王星サイズの天体との散乱遭遇のため) ことを示しています。
天体)、そして海王星が到達したとき、海王星の離心率は eN ≃ 0.03–0.1 まで励起されたと考えられます。
≃ 28 天文単位 (おそらく惑星クラスの天体との遭遇によるもの)。
ここでは SDO について考えます。 SDO は、散在する集団と孤立した集団に分類できます。
グラッドマンら。 (2008) は、散乱 SDO を動的に結合されるオブジェクトとして定義しました。
海王星 (1000 万の長い積分ウィンドウで長半径変化 ∆a > 1.5 au、プラス
a > 47.8 au)、分離された SDO は結合されていないものとして (非共振、Δa < 1.5)
au、および古典的な KBO を避けるために e > 0.24)。 ここでは、より単純な定義を採用します。 私たちは避けます
の形成に関する議論を混同したくないため、< 60 au の軌道を使用します。
遠隔/分離したSDOと、強い5:2共鳴への物体の捕捉に関連するSDO ≃ 55.5 au (Gladman et al. 2012)。 60 < a < 500 au のオブジェクトは次のように分離されます。
近日点距離 q = a(1−e) < 35 au (散乱 SDO) および q > 35 au のもの
(分離された SDO)。 Gladman らの定義とよく一致します。 (2008)
q < 35 au の SDO は通常海王星によって散乱されるのに対し、q > 35 の SDO は海王星によって散乱されるためです。
auは違います。 重要なのは、同じ(私たちの)定義をモデルと観測されたものの両方に適用することです。
人口 - これにより、2 つを正確に比較できるようになります。
この取り組みにおける私たちの当面の目的は、孤立した人々の長年の問題を解決することです。
SDO。 この問題は図 2 に示されており、偏ったモデルは放射状プロファイルを示しています。
観測よりも大きな軌道半径では分離した SDO がはるかに少なくなります。1 何かが明らかにあります。
ここを離れてください。 放射状プロファイルの問題は、これまでにテストしたすべての移行モデルに存在します。
具体的には、次の条件でモデルをテストしました。 (1) 海王星の移動のさまざまなタイムスケール (τ = 5、(10、30、100 Myr)、
(2) 海王星の離心率の異なる励起 (e.g.、eN = 0、0.03および 0.1)、
(3) 海王星の離心率の異なる減衰タイムスケール (e 倍 τe = 5、10、30)
(4) 元の微惑星円盤の異なる半径方向プロファイル (Nesvorn´y etアル。 2020)、および(5)不安定時の海王星のジャンプの有無。
問題
銀河ポテンシャル/星がモデルに含まれているかどうかとは無関係に存続します (Nesvorn´y et al. 2017)。 さらに、この問題は当初、
このモデルは太陽系外縁起源調査 (OSSOS) の検出結果と比較されました。
Dark Energy Survey (DES) の観測結果と比較すると、さらに明らかです。
SDO (Bernardinelli et al. 2022) (図 2)。
私たちは現在、この問題に対する興味深い解決策を見つけたと信じています。 それをテストするために、私たちは
Adams は、星団を使用して新しいシミュレーションを実行しました (Adams 2010)。 クラスターの可能性と
星団星との遭遇は、Batygin et al. に記載されている方法に従ってモデル化されました。
(2020) (セクション 2)。 他のすべての側面では、力学モデルは同じままでした。 議論していくうちに
昆虫。 図3に示すように、新しいモデルは、50 天文単位未満で KBO の同じ軌道分布を生成しました。
ただし、50 au を超える場合、分離された SDO のモデル母集団はより放射状に広がります。
クラスター効果を考慮した場合。 さらに、特に次のように仮定すると、
恒星接近は早い段階で発生しており、モデルは放射状と正確に一致することができます。
DES によって検出された分離した SDO のプロファイル (Bernardinelli et al. 2022; Section 3)。
恒星クラスター効果は、極端な KBO を説明するために以前に援用されました (Kenyon と
ブロムリー 2004; モルビデリ&レヴィソン 2004; ブラッサーら。 2006年、2012年。 ブラッサー&シュワンブ
2015)、(90377) Sedna および 2012 VP113 (a > 200 au、q ≃ 75–80 au; Brown et al.
2004、トルヒーヨ&シェパード 2014)。 結果は、太陽が星団の中で誕生したことを示しています
N 〜 10^3 以上の星があり、太陽が少なくとも T 〜 10 の間星団内に留まったこと
ミル。 ただし、極端な KBO は少数しか知られていないため、これらの結果は小さな影響を受ける可能性があります。
数値統計。 さらに、極端な KBO はさまざまな観測で検出されました。
異なる検索戦略を採用し、異なる限界値を持ったプログラム。 それ
したがって、その検出に関与する強いバイアスをどのようにモデル化するかは明らかではありません。 あれは
35 < q < 50 au の分離された SDO の放射状構造はなぜよく特徴付けられているのか
DES 観測 (> 50 au で検出された ≃ 200 個の KBO) から、有用な情報を表すことができます。
クラスターのプロパティに対する制約。
6. 結論
私たちは、切り離された SDO の放射状分布に関する長年の問題を指摘しました。
そして、太陽が特に接近した場合、この問題は解決できることを示しました。
星団星 (例: 質量 ≃ 0.2 M⊙、最小距離 ≲ 200 の M 矮星)
オー)。 このような接近遭遇により、フェルナンデス雲オブジェクトの大規模な集団が形成され、
この集団は a < 200 au および q < 50 au まで広がり、放射状構造に影響を与えます。
ダークエネルギー調査によって検出された分離した SDO の数 (Bernardinelli et al. 2022)。 私たちは
この効果を詳細に文書化するために 3 つの新しいシミュレーションを実行しました。 軌道分布
さまざまなモデルで取得された分離された SDO の一部は、DES シミュレーターでバイアスされ、
観測結果と 1 対 1 で比較します。 同じ方法を以下にも適用しました
十数の以前のモデルは、特性に関する仮定が異なりました。
海王星の移動ですが、星団の影響は含まれておらず、海王星の移動の影響に関連する多くの可能性を排除できることを示しています。
ディスク の散乱体の放射状構造における惑星9または浮遊惑星の影響の調査は将来の作業のために残されています。

図 1.— 偏りのあるモデル (黒線) と OSSOS 観察の比較
ホット クラシックの (赤い点) (40 < a < 47 au、q > 36 au、i > 5)
◦; ネスヴォルニーら。 2020年)。 の
固有モデルの分布は破線で示されています。 斜線部分は 1σ (太字グレー)、
2σ (中) および 3σ (ライトグレー) エンベロープ。 モデルの結果を使用して、10,000 個のデータを生成しました。
それぞれ 164 体からなるランダム サンプル (サンプル サイズは OSSOS の数と同じ)
検出)。 サンプルには OSSOS シミュレーターを使用してバイアスをかけました (Lawler et al. 2018)。
サンプルの 68.3% (1σ)、95.5% (2σ)、および 99.7% (3σ) を含むエンベロープを特定しました。
それらをここにプロットしました。 下のパネルは、低偏心移動を備えたモデルを示しています。
海王星の値 (eN ≃ 0.01)。 この場合、軌道は香西によって海王星から切り離されます。
共鳴 (Kozai 1962) により、軌道が非常に少ない特定の傾斜分布が作成されます。
15°未満
(ネスヴォルニー 2021)。 上のパネルは、Neptune の成功モデルを示しています。
海王星が ≃ 28 au に達したとき、離心率は eN = 0.1 まで励起され、ゆっくりと減衰しました。
その後。 K-S テストは、成功者と成功者からの傾斜分布に適用されました。
(偏った) モデルでは、失敗したケースの確率はそれぞれ 37% と 10−10 未満です。
そして、観察された分布は、同じ基礎となる分布から抽出されます。 適合図
Nesvorn´yらより。 (2020年)。

図 2.— 切り離された SDO の問題。 プロットは、偏ったデータ間の比較を示しています。
銀河シミュレーションとダーク エネルギー サーベイ (DES) 観測からのモデル (黒線)
切り離された SDO の (赤線)。 セクションを参照してください。 2 モデルパラメータと DES の説明
(Bernardinelli 他、2022)。 固有モデルの分布は破線で示されています。 見る
斜線部分の意味については、図 1 のキャプションを参照してください。 コルモゴロフ・スミルノフ (K-S) 検定
長半径分布 (パネル a) に適用すると、
偏りのあるモデルと観察された分布は、同じ基礎となる分布から抽出されます。

図 3. 最初の 1000 万年後の恒星との遭遇。 パネルは上から下に表示されます。
この研究で考慮される 3 つのケースでの遭遇: (1) 星団なし、太陽との遭遇
銀河内の恒星 (銀河というラベルが付けられている)、(2) 比較的遠くにある恒星と遭遇する星団
(クラスター 1)、(3) 比較的近い恒星に遭遇したクラスター (クラスター 2)。 サイズ
シンボルは星の質量と相関します。 Cluster2 の最接近遭遇は次のとおりです。
0.17 M⊙ の星が最小距離 d ≃ 175 au で通過するとき、t ≃ 5.17 Myr。 効果
この遭遇について、KBO の傾斜分布と惑星軌道について議論します。
セクション 4 で。

図 4.— 3 つのモデルからの物体の軌道分布: (1) クラスターなし (ラベル付き)
(2) 比較的遠くに星が出現した星団 (Cluster1)、(3) 星団
比較的近い恒星との遭遇が見られます (クラスター 2)。 すべてのシミュレーションには銀河潮汐が含まれています
そして太陽と銀河の星との出会い。 モデル母集団をサブサンプリングしました。
ここでは、シミュレーション時刻 t = 4.6 Gyr (現在の時代) を、制限するために 4 倍して示しています。
飽和。 赤い三角形は、既知の極端な KBO の軌道を示しています。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます