
天王星系に探査機を送り込むなら最大の衛星チタニアを目標にするのが普通だろう。天王星系最大の衛星と言っても重さは月の20分の1、大きさは半分以下の0.45 チタニアもそれなりに重力が有る天体だけど天王星が近すぎるから安定した軌道の範囲は狭そうです。マヌーバ(軌道修正)を行うことで周回軌道をキープできる。以下、機械翻訳。
宇宙探査機のチタニア周回軌道操作
2024年12月29日
抽象的な
ほとんどの宇宙ミッションでは、探査機がミッションターゲットの周囲にかなり長い時間留まることが興味深い。ミッションの寿命が長いほど、周回する物体に関する情報収集の機会が増える。この研究では、宇宙探査機がチタニアの表面と衝突するのを回避する方法を示すことを目的とした軌道操作を紹介する。重力ポテンシャルを2次まで拡張することで、係数による重力場の非対称性が明らかになる。
C22チタニアの帯状係数J2
、および天王星の重力摂動が検討されている。共面バイインパルス操作の 2 つのモデルが提示されている。最初の操作は、最初の楕円軌道を最終的な円軌道に移行するもので、2 つ目の操作は、最初の楕円軌道をやはり楕円である最終的な軌道に移行することを目的とする。操作を実行する前に、軌道の傾斜角と半長軸の遅れが調査される。操作を実行するための最良のシナリオを指摘するために、移行を行うことができる軌道上のさまざまなポイントについての研究が提示されている。さらに、近点引数の変動を修正するための操作戦略が提示されている。結果は、統合の数日後に実行される操作が、衝突の数日前に実行される操作よりも経済的であることを示しています。操作の経済性は、速度の増加と寿命の比率の分析によっても実証されています。
キーワード:軌道、操縦、寿命、天体力学、数値シミュレーション、惑星衛星
1導入
近年、太陽系のガス惑星に宇宙ミッションを送ることへの関心が高まっています。ビブ1NASAとESAは、2024年から2037年にかけて氷の巨星へのミッションを計画している。これらのミッションは、これらのシステムの起源と進化を理解するのに役立つ可能性がある。さらに、いくつかのミッションは、2023年に打ち上げられ、木星とその衛星であるガニメデ、エウロパ、カリストを調査する木星ICy衛星探査機(JUICE)ミッションなど、特定の自然衛星に向けられている。グラッセ2013。
いくつかの研究は、自然衛星の周りのより良い軌道を探しています。これらの研究の目的は、これらの衛星をターゲットとする将来の宇宙ミッションに役立つ重要なデータを提供することです。しかし、探査機を宇宙に送り込むことは、多くの時間と投資を必要とするプロセスです。ミッション中、探査機が観測対象の天体の周りを長期間にわたって周回することが望ましいです。したがって、目的の物体の観測を成功させるには、長期間の軌道を探し、ミッションターゲットとの衝突を回避することが非常に重要です。
作品ザビエル2022氷の巨大惑星である天王星の衛星の一つであるティタニアの周回軌道に関する研究を発表する。著者らは、さまざまな離心率を持つティタニアの周回軌道を調査している。第3の天体による摂動とティタニアの重力係数を考慮し、寿命マップから寿命の長い軌道を見つける。数値シミュレーションの結果、寿命が最も長い軌道は離心率が10^−3
著者らはまた、近点引数と昇交点経度をゼロ以外の値にすると探査機の寿命を延ばすことができることを示している。さらに、ティタニアの重力係数の誤差による寿命感度に関する研究では、離心率が10^−3これらの潜在的なエラーの影響を最も受けます。
長期軌道は、タミス2022この場合、天然衛星は木星のガリレオ衛星の 1 つであるイオです。著者らは、探査機の衝突や脱出の可能性を検出することができました。重要な寿命を持つ軌道は、6 か月から 2.3 年の範囲でした。さらに、この研究では、イオの周りの軌道は摂動源からの距離が短いため、摂動の影響を受けやすいことが示されました。最後に、著者らは、近点引数と昇交点の経度にゼロ以外の値を割り当てることの重要性を強調しました。
によって開発された作品チネリ2022天然衛星エウロパの周囲を低高度かつ高度傾斜の高い軌道で周回する探査機の寿命に関する研究結果が発表されました。その結果、第 3 天体の傾斜角と交点位相が探査機の寿命に影響を与えることが示されました。
自然衛星の周回軌道を長期間研究するには、提案されたミッションターゲットとの探査機の衝突を回避する方法を見つける必要がある。この意味で、チネリ2019、エウロパ周回軌道修正操作が提案されている。その結果、適切な修正操作戦略によって寿命を延ばすことができることが示された。軌道修正操作は、フェレイラ2022著者らは、土星の天然衛星タイタンの周りの長期軌道を分析した後、このような操作を実行するための最良の結果を提示している。
上記を踏まえ、本稿では、探査機がティタニアの表面と衝突するのを回避するための軌道操作のモデルを提示する。最初の操作では、探査機を初期の楕円軌道から最終的な円軌道に移行することを提案する。2 番目のモデルでは、初期の楕円軌道から最終的な楕円軌道への移行であり、両方とも同一平面上にある。この 2 番目のモデルでは、軌道のさまざまなポイントで操作を実行し、操作を衝突の近くで行うか、ミッションの存続期間の 2、3 日以内に行う方が実現可能かどうかを分析した。また、近点引数の小さな変動を修正するための操作モデルも提示する。これらの操作は、半長軸の偏差と離心率が小さいポイントを考慮して実行された。
2 数学モデル
ここで使用されるシステムには、中心天体としてのティタニア、ティタニアの周りを周回する宇宙探査機、そして第3の天体としての天王星が含まれる。天王星はティタニアの周りを半径1.5メートルのケプラー軌道で周回すると想定されている。
25.362×10^3 kmと質量8.68×10^25 kg ( https://ssd.jpl.nasa.gov/ )。数値シミュレーションで使用した軌道要素は表1に示す。また、チタニアの2つの主要な重力項も考慮する。
J2そしてC22、値は1.13×10^−4そして3、38×10^−5
、 それぞれチェン2014これらは、重力場においてケプラー項に次いで最も重要な項である。これらの項は、軌道の離心率や傾斜角など、いくつかの軌道要素に大きな変化をもたらす。このように、これらは物体の不規則な形状をモデル化するのに最も効果的な項となる。ツィルト2009;ツィルト2010;ザビエル2022チタニアの場合、これらの項が文献で利用可能な唯一のものであることは注目に値する。これらの係数に加えて、チタニアの質量(35.27×10^20kg)とその半径(788.9
この研究では、100km以上の距離の探査機が対象とされている。探査機の運動方程式は次のように表される。シーレス2006:

どこP→Tチタニアの重力ポテンシャルの2次までの拡張である。
PTx、PTyそしてPTzの構成要素であるPTベクター。
m宇宙探査機の質量はMTチタニアの質量とMu天王星の質量。
r→そしてr→uはそれぞれ探査機と天王星の半径ベクトルです。
表1:天王星に対するチタニアのパラメータ。
パラメータ 価値
半長径(km) 435.8×10^3
偏心 1.18×10^−3
傾斜(∘) 1.0×10^−1
近点引数(∘) 1.64×10^2
昇交点の経度(∘) 1.67×10^2
平均異常値(∘) 2.05×10^2
JPL ウェブサイト: https://ssd.jpl.nasa.gov/。
まず、軌道は方程式1 - 4で記述されるシステムを考慮して数値的に積分された。これらの数値積分中に、操作が行われた。軌道を積分し、操作を実行するために、マーキュリーパッケージに変更が加えられた。チェンバース1999。
2.1 軌道操作
軌道の減衰過程において、軌道要素は変化する。したがって、軌道操作を行う際には、半長軸(a)、偏心率(e)、傾斜(i)。たとえば、探査機がミッションターゲットの表面に衝突する直前で操作が行われたとします。その場合、軌道の離心率は大きくなり、長半径にかなりの変動が生じる可能性があります。したがって、このセクションでは、2 つの操作モデルを紹介します。最初に、初期の楕円軌道から最終的な円軌道への移行を検討し、その後、宇宙船を初期の楕円軌道から最終的な楕円軌道に移行させて、傾斜角を考慮せずに軌道の元の高度を修正します。両方の操作は共面です。最終軌道はミッションの目的の軌道であり、初期軌道は摂動が作用して初期軌道が変更された後の軌道です。
2.1.1 楕円軌道から円軌道への操縦。
ここで紹介する最初の操作は、宇宙探査機を楕円軌道から最終的な円軌道に移行することです。最初のインパルス(ΔV1)が楕円軌道の遠点に印加され、探査機はトランスファー楕円軌道に入る。2番目のインパルス(ΔV2) は、探査機がトランスファー軌道の遠点にあるときに適用され、探査機が最終的に希望する円軌道を占有するようにする。速度の総増分は、モジュール (ΔV1) そして (ΔV2軌道遷移を実行する時間は、遷移軌道の周期の半分です。この操作を実行するための方程式は次のように記述されます。


どこVap初期軌道の遠点における速度である。
Vp1移行軌道のポイント1における速度、ΔV1最初の衝動V2は移行軌道の遠点(点2)における速度である。
五c私r最終的な円軌道の速度、ΔV2
2番目の衝動とΔ五総衝動。
2.1.2 楕円軌道間の移動
この研究で紹介するもう一つの操縦は、最初の楕円軌道から、同じく楕円である別の最終軌道への操縦である。これらの軌道は共面である。これは、宇宙船の公称軌道が楕円である場合に起こる。この操縦では、最初のインパルス(Δ五1) は、最初の楕円軌道の近点に印加され、その後、探査機はトランスファー軌道に投入される。2 回目のインパルス (Δ五2) がトランスファー軌道の遠点に適用され、宇宙船は最終的な楕円軌道に配置されます。(Δ五1) そして (Δ五2) は、操作を実行するための速度の合計増加分になります。このような操作を実行するための方程式は次のように表されます。

どこrp1そしてra1初期軌道の近点と遠点です。さらに、rta転送楕円の遠点である。
rp2最終軌道の近点である。ra2=rtaは、望ましい最終軌道の遠点である。速度の増加に関しては、
Vp1初期軌道の点1における速度に等しい、Vpt移動楕円の点1における速度、ΔV1最初の衝動Vat
移動楕円の遠点における速度、Va2最終的な目標軌道に関する点2の速度、ΔV2 2番目の衝動とΔV総衝動。
3 結果の分析
最初に提示された結果は、最初の楕円軌道から最終的な円軌道への最初の操作に関するものである。これは、公称軌道が円で、摂動後の軌道が楕円である場合に発生する状況である。次に、最終的な望ましい軌道の半径は、最も長い軌道継続時間を持つ領域に従って選択された。これは、ザビエル2022この半径は1000~2000 kmの範囲で、200 km間隔で変化します。操作を実行する適切なタイミングの選択は次のように行われました。まず、初期の長半径が(ai=Ri)で、この軌道の減衰を分析し、開始位置からの変化が大きな値に達したときに操作を実行します。この点の軌道要素を取得し、それらを初期軌道の要素と見なします(黒い軌道、図1)。軌道の初期条件の小さな変化は、その寿命を短くし、軌道は大きな離心率と傾斜角に達します。したがって、初期位置の大幅な変更後に、傾斜角を無視して軌道を元の高度位置に戻す操作がいくつか実行されます。4つの初期傾斜角が検討されました。60∘、70∘、80∘そして90∘
図1は、操作がどのように実行されるかを示した図です。

図1:望ましい最終的な円軌道の表現。Rf軌道の半径です。紫色はRf=1000 km、緑Rf=1200 km、青はRf=1400 km、赤はRf=1600 km、ライトグリーンRf=1800 kmと濃い紫色Rf=2000 km。初期軌道は黒線で表されます
操縦を計画するために、私たちはチタニアの重力係数を考慮しました。
J2そしてC22、および天王星の重力係数も取得しました。その後、式6~11を利用して、目的の軌道を達成するために必要な操作を実行しました。
初期値の20~30%の最大偏差を持つ軌道(黒い軌道、図1)は、初期傾斜角が
60∘、70∘そして80∘全てのシミュレーションで、軌道が偏差に達すると寿命は240~250日に近づき、
ΔV再び半径1000kmの円軌道に到達するのに必要な距離は約
1×10^−2−6×10^−2 km/s。この傾斜角の軌道の総寿命が 252 日であることを考慮すると、最大の傾斜角の変化は衝突の数日前に発生すると結論付けられます。
初期傾斜角が90∘、最大の変動I最終軌道の5%である。しかし、
ΔV範囲は4×10^−2−1×10^−1 km/sで、減衰時間は1~17日の範囲です。
ΔV半径1000~1200kmの最終軌道に到達するための操作です。これらの軌道では傾斜角の変化率が最も高くなります。
長半径の変化は非常に小さく、初期値の0.1~0.9%の間です。分析された4つの傾斜については、
60∘、70∘、80∘そして90∘、半径の最大変化が0.6 - 0.9 %になるケースがあります。これらのケースでは、ΔV範囲は8×10^−2−1.1×10^−1 km/s。最も低い値を示したケースはΔV最終軌道は半径1000~1200kmです。
いくつかのミッションでは、宇宙船の位置が大きく変化する前に、短い寿命で位置を修正することを選択します。たとえば、図2は、最小値を見つけようとする研究を示しています。
ΔV軌道遷移を実行する前に、初期位置が大きく変化する。したがって、ここで注目する操作は、傾斜角または長半径の大きな変化を伴う操作ではない。以前のケースと同様に、分析した4つの傾斜角について、最小ΔV最終軌道の半径が 1000 ~ 2000 km の場合に計算されます。

図2:最小ΔV最終軌道の円半径の関数として。4つの初期傾斜を分析する
60∘、70∘、80∘そして90∘それぞれオレンジ、赤、緑、黒の色です。初期値:ai=Ri=1000−2000 キロメートル、ei=0そしてω=Ω=0∘
予定されている最終軌道の半径は1000−2000 キロ。図2に示すように、Δ五およそ5.4×10^−5
全ての傾斜角において、最終軌道半径1050kmの速度は毎秒1000kmである。
60∘、軌道修正は5日後に実行され、これは約45軌道周期に相当します。その時点で、軌道長半径と離心率は次の値でした。
1.0498×10^3 kmと2.8×10^−4それぞれ、長半径の変化率は0.016初期値の%と0.45傾斜の%。
軌道傾斜角が70∘この作戦は14日後に実行され、1つのそしてeは1.0492×10^3 kmと2.3×10^−4、それぞれである。このΔVは0.4%、長半径については0.01%.
Iのために等しい80∘そして90∘、最小ΔVは5日後に発見される。
I=80∘、操縦の瞬間、半長軸の値は1.0497×10^3 kmと離心率2.0×10^−4傾斜角と長半径の変化は0.36% そして0.02%である。90∘、この操作は、a=1.0497×10^3 kmとe=2.03×10^−4傾斜の変化はおよそ0.3% および半長軸上0.023%。この最小範囲内では、半径950kmの最終軌道の場合、ΔV軌道変更に必要な速度は、他の解析例よりも大きい。初期傾斜角が80∘そして90∘これらの値は5.7×10^−4 km/sの場合I=80∘そして5.55×10^−4 km/sの場合I=90∘。 のためにI=70∘この軌道はΔV=7.1×10^−4 km/秒。
表2:の価値ΔV軌道傾斜角と軌道長半径に大きなオフセット値を持つ軌道変更の場合。軌道傾斜角、軌道継続時間、遠点半径(rapo)、最終円軌道半径(rc私rc)、長半径オフセット(Def a)、傾斜角(Def I)のパーセンテージ、およびそれに相当する
ΔV。

最良の値を分析するためにΔⅤ軌道操作を行うために用いられるいくつかの値を示す表2は、ΔⅤ傾斜角と長半径が遅れている軌道に使用されます。各傾斜角について、I= 60∘、I= 70∘、I= 80∘そしてI= 90∘、の値ΔVおよび操作を実行するための初期条件が提示されています。半径が 1000、1200、1400、1600、1800、および 2000 km の最終軌道のケースが提示されています。
次の議論は、2つの楕円軌道間の操作で得られた結果についてである。ザビエル2022離心率が等しい物体の軌道の減衰は、
10^−4、10^−3、10^−2そして10^−1研究されている。著者らは、軌道離心率が大きいほど寿命が長くなると結論付けた。
10^−3したがって、この研究で調査された最終的な軌道は、その研究で研究された軌道と同じ離心率を持っています(10^−4、10^−3、10^−2そして10^−1)。これを偏心と呼ぶ。
ef図3にこれらの軌道を示します。
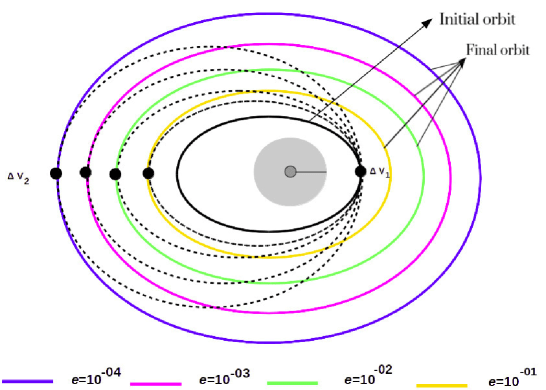
図3:最終的な楕円軌道の表現。オレンジは離心率10^−1緑は10^−2、ピンク10^−3青は10^−4。
それぞれの偏心に対する操作を実行するために、一連の数値シミュレーションが作成されました。
軌道上の6つのポイントが、各値に対して操作を実行するために選択されました。
e
この選択は、衝突前に複数の操作を異なる時間に行う方が実現可能か、それとも周回機が衛星に衝突する直前に1回だけ操作を行う方が実現可能かを分析することを目的としています。このような操作は𝐦𝐏、𝐦𝟏、𝐦𝟐、𝐦𝟑、𝐦𝟒そして𝐦𝟓。 いる
メートル
P、この操作が主な操作である理由は、この操作がティタニアの表面に最も近い地点、つまり衝突に最も近い地点で実行されるためです。この操作のおおよその近点は、すべての値で790 kmです。
e
. 操縦のポイントm5
ティタニアの表面から最も遠く、数日間の減衰で操作が実行される。
mp. の近点はm5約965kmです。m1、m2、m3、 そしてm4演習は中間地点で行われるmpそしてm5の近点はm1約825kmです。
m2≈860 キロメートル、m3≈895 キロメートル、m4≈930 kmとm5≈965 km。ポイントは35kmごとに変わります。
すべてのシミュレーションは以下を考慮して行われた。
a=1000 キロメートル、
I=90∘、ω=Ω=0∘、重力係数
J2そしてC22チタニアと天王星の重力の影響。
最初の一連の操作は、e=10^−4、総寿命は268.536日となる。軌道操作で考慮されるすべてのポイントは、図4(上部)に示されている。操作を実行する際のいくつかのパラメータの変化を関連付けるために、図4(下部)は、近点の位置(rp)、eそしてI時間の関数として。この図では、各操作が実行された日も視覚化できます。


図4:実行された6回の軌道位置の投影(mP、m1、m2、m3、m4そしてm5) のためにe=10^−4(上部)軌道要素の変化e、i
、および寿命と操縦時間の関数としての近点半径(下部)。初期条件:a=1000 キロメートル、
e=10^−4、i=90∘、ω=Ω=0∘。メイン作戦 mPパラメータは次のとおりです。a=9.993×10^2 km、e=2.094×10^−1、i=87.9∘
、近点は790.0 km、遠点は1208.59 km、軌道変更時間は267.26日です。これらの値を考慮すると、近点は約21%、傾斜角は2.3%、長半径は0.1%減少します。離心率も3桁増加しています。
mP衝突の約1日前に操縦が行われた。推定
ΔVこの移転は≈5.26×10^−2 km/s。この操作の位置は、図4の赤い点線で示されています。
2番目の操作(m1)、 のためにe=10^−4は、衝突の約 8 日前に、数値積分の 259.87 日以内に実行されました。この選択された時点で、軌道の近点は 825.09 km で、初期値の約 17.5% でした。その他の初期条件は次のとおりです。
a=9.989×10^2 km、e=1.740×10^−1、i=88.3∘
、遠点高度は1172.88kmである。この操作を実行するには、ΔV使用されたのは約4.34×10^−2 km/s。この軌道要素の変化を分析すると、259.87日間で近点が約180km減少し、傾斜角が1.4∘軌道半径は2km拡大した。m1図4では青い点線で表されます。
この操作(m2)は、衝突の約19日前、248.59日後に実行されました。この操作では、ΔV離心率の軌道に到達するのに必要な10^−4だった
3.45×10^−2 km/s。操作を実行するために次の初期条件が使用されました。a=9.991×10^2 キロメートル、e=1.392×10^−1、i=88.5∘
、近点は 860.01 km、遠点は 1138.35 km です。軌道の減少中に軌道要素のすべての変化の中で最も変化率が高いのは近点です。近点はほぼ 14% 減少しました。軌道長半径と軌道傾斜角はそれぞれ 0.1% と 1.66% 減少しました。離心率の場合は、初期値から 3 桁増加しました。図4のオレンジ色の線は、この操作を表しています。
図4では、操作を表す色(m3) のためにe=10^−4緑色で表示されます。この操作の有効期間は234.86日で、衝突の約33日前でした。この操作では、近点距離は初期値の999.9kmから895kmまで約10%減少しました。離心率は2桁増加し、e=9.970×10^−2、遠点高度は103km近く上昇した。長半径と傾斜角はそれぞれ0.1%と1.22%と小さな変化であった。
m3以前の軌道要素のオフセットは小さいが、その操作が行われる地点はミッションにとって興味深いものであり、ΔV必要なのは2.56×10^−2 km/秒。
(m4)は、図4で水色で示されており、マヌーバ実行に要した時間は218.20日であった。マヌーバは衝突の50.34日前に行われ、その近点は930.16kmで、初期値と比較して約7%低下した。傾斜に関しては、変化は小さく、約1.33%であった。
6.95×10^−2そしてΔVの1.70×10^−2 同じ原点位置に到達するために km/s が使用されました。
ピンク色の最後の動きe=10^−4図4に示すのは、軌道が187.84 すでに述べたように、この操作は他の操作よりもミッション開始からより短い日数で実行されるため、近点の減衰はより小さくなります。この点の初期条件はa=9.991×10^2 km、e=3.420×10^−2、I=89∘、近点は965.01km、遠点は1033.37kmである。近点オフセットは≈3.5%そしてその傾向≈1.11%速度増加を伴うΔV=8.31×10^−3 km/秒。
実行されたすべての操作を比較すると、e=10^−4、最善の策は(m5)。ΔVの8.31×10^−3 km/sは、生存日数に対してはるかに小さい。他の操縦と比較すると、(mP)例えば、2つの操作(m5)が実行されると、軌道の寿命は最大374日となり、2×ΔV等しい1.662×10^−2 km/s。2つの操作(mP)、私たちは一生≈534 日ですが合計ΔVの1.052×10^−1 km/s、総速度の約6倍ΔV(で使用されるm5)。もし、操縦のポイントで6回の操縦を行えば(m5) 、寿命が長くなり、燃料消費量が少なくなります。この比較は他の操作にも当てはまります。
以下の議論は計算のためのものであるΔ五のためにe=10^−3結果は、e=10^−4
、操作ポイントの投影図は省略します。前回と同様に、操作を実行するために軌道上の 6 つのポイントが選択されました。この場合、軌道継続時間は 313 日でした。
のm1この操作は衝突の 8.56 日前に 304.44 日間にわたって行われた。この操作では、近点は初期値より 17.4% 小さい 825.18 km、遠点は減衰前の値より約 15% 大きい 1157 km とされた。その他の初期条件は以下のとおりである。
a=9.999×10^2 km、e=1.747×10^−1、I=87.9∘の価値ΔVおよそ4.33×10^−2 km/sの値を比較するとΔV見つかったm1前の場合、値が非常に近く、違いは無関係であることがわかります。
機動用m2我々は、衝突の約18日前の295.15日の操縦時間という初期条件を使用しました。a=9.996×10^2 km 、e=1.396×10^−1、I=88.0∘
、近点は860.10km、遠点は1139.22kmです。パラメータの変化に関しては、近点では約14%、傾斜角では2.2%の減少がありました。これらの初期条件で、
Δ五の≈3.43×10^−2 km/s。前回の演習と同様に、ΔVのためにm2に非常に近いΔV同じ操作がケースで分析されたe=10^−4。
でm3、ΔVV見つかったのは2.54×10^−2 衝突の30.96日前の282.04日の間に、軌道は秒速kmで回転した。この時点で、軌道の長半径は
9.990×10^2 km、離心率1.041×10^−1、傾斜は88.2∘近点変動は10.4%、遠点変動は10.2%近く増加した。m3分析された値と類似の値も持っている
e=10^−4。 のためにm4、の値ΔV見つかったのは≈1.68×10^−2 264.93日間、毎秒キロメートルの速度で飛行した。これらの軌道変更では、近点の減少はほぼ7%、傾斜角は≈1.5% 近点は930.03 km、遠点は1069.74 km、離心率は6.986×10^−2同じ操作を分析すると、10^−4の値はΔV近づいています。
軌道遷移の初期条件はm5検討されたのは:a=9.989×10^2 km、e=3.388×10^−2、I=88.9∘、近点965.05km、遠点1032.76kmであった。結果は、ΔV=8.01×10^−3 km/s、減衰≈3.4%近点から≈1.22%傾斜角と寿命は234.19日で、衝突の約79日前です。
同様の分析を実施し、e=10^−4、今回はm5そしてm1、我々は、この操作に注目するm5最も実現可能な方法です。
m5過ごした8.01×10^−3 生後234日目に操縦を行うには、m1過ごした4.33×10^−2 304.44日間の人生でkm/s。2回の操縦を行えばm5探査機は468.38日間軌道上に留まり、合計ΔVの1.602×10^−2 km/s。2回の操縦の場合m1、合計ΔVだろう8.66×10^−2 608日強の寿命で毎秒キロメートルの速度で走行し、これはΔV 2つの操作に使用されるm5。
グラフで見ると、e=10^−2これらは、e=10^−1については後ほど紹介しますが、ここでは省略します。e=10^−2、その作戦mPは、ΔVの4.99×10^−2 km/sの値と比較するとΔVのためにmPの場合e等しい10^−4そして10^−3この値はわずかに低く、5%この操作では、近点オフセットは 20.2% で、傾斜角はわずか 0.6% でした。使用されたその他の初期条件は次のとおりです。a=9.988×10^2 km、e=2.089×10^−1、I=89.4∘ 遠点高度は 1207.00 km です。この操作は 152.68 日、つまり中心天体との衝突の 0.5 日前に発生しました。
の場合m1、機動時間は衝突のほぼ7日前(145.90日)であり、近点(825.01km)で約17%、傾斜角で1.2%減少しました。
ΔV転送を実行するために必要なのは≈4.10×10^−2 km/s。半径は9.995×10^2 km、離心率は1.745×10^−1遠点高度は1174.00kmである。
m1 また、同じ近点に対して、以前のケースで分析された操作よりもわずかに低い値(約 5%)を示しています。
所要時間はm2 135.00日、数値積分終了の18日前でした。この操作を実行するには、ΔVの≈2.92×10^−2 km/sが見つかりました。
ΔVケースについてe=10^−4そしてe=10^−3、ΔV今では約15%小さくなっています。当初の楕円軌道はa=9.991×10^2 km、e=1.389×10^−1
、i=89.6∘、近点は860.26 km(≈13%初期値より小さい)、遠点高度は1137.90 km(≈13%初期値より大きい)。
作戦のためにm3衝突の約 30 日前に実行された軌道の初期条件は次のとおりです。a=9.989×10^2 km、e=1.039×10^−1、I=89.5∘、近点は895.07kmで、ほぼ9%の減少で、遠点は1102.80kmで、初期値より約93km増加しました。速度の総衝撃は≈2.31×10^−2 km/sです。この値は、ΔV症例で発見e=10^−4そしてe=10^−3。
水色で表された操作は、m4 104.85日で起こった。速度の増加を見つけるにはΔVこの時点で、6%の変化を伴う近点が考慮された。傾斜角は約0.3%、操縦の瞬間まで。これらの初期条件では、長半径は9.993×10^2 km、e=6.931×10^−2、i=89.7∘、近点は930.07km、遠点は1068.6kmで、ΔVの1.45×10^−2 km/sという値が見つかりました。この値は、m4以前のケースでは。
最後の作戦、m5、 のためにe=10^−2は、生後74.11日後に実施されました。初期条件は次のとおりです。
a=9.999×10^2 キロメートル、e=3.482×10^−2、i=89.8∘、近点は965.14kmで2.5%の減衰、遠点は1034.7kmである。この場合、ΔVだった6.04×10^−3 km/秒。
離心率のある最終軌道に向けて実行されるすべての操作において10^−2、ΔV同じ操作で得られた値よりも低い値を示した。e=10^−4そしてe=10^−3パーセンテージで言えば、mP≈5%、m1≈5%、m2≈15%、m3≈9%、m4 15%から17%の間m5 25%から27%小さくなるe=10^−2以前のケースと比較して。
機動m5再び、これが最も良い作戦として発見された。ここでは、この作戦をm2 2つの操作を行うm5軌道寿命は約148日で、合計ΔVの1.208×10^−2 km/s。しかし、2回の操縦を行うとm2、軌道の寿命は合計270日になりますΔVの6.38×10^−2 km/sです。寿命はm2、ΔVのためにm5約5.2倍小さくなります。


図5:実行された4つの操作の軌道位置の投影(mP、m1、m2そしてm3) のために
e=10^−1(上部)軌道要素の変化eそしてI寿命と操縦時間の関数としての近点半径(下部)。初期条件:
a=1000 km、e=10^−1、i=90∘、ω=Ω=0∘シミュレーション時間は52日間です。
最後に、図5に、以下の操作の結果を示します。e=10^−1この場合、我々は4つの操作のみを考慮する。
mP、m1、m2、 そしてm3この選択は、軌道の初期近点が990kmから始まるため、操縦のためのポイントが
m4(近点距離は930km)とm5(近点距離は965km)は不可能です。色と点は、前の場合と同じです。
mPにm3この場合、合計統合時間は 52 日でした。
のmP軌道修正は、近点790km、遠点1209.5kmを考慮して行われた。9.998×10^2 km、e=2.098×10^−1そして
I=89.5∘総インパルス2.74×10^−2 km/sは衝突のほぼ1日前に与えられた。操縦の時点で、近点オフセットは約12.2%、傾斜角は0.55%であった。
ΔV分析されたmP前の例では、見つかった値は、e=10^−2、ほぼ48%小さくなりますe=10^−3そしてe=10^−4。
の場合m1速度の増加は衝突の約8日前、42.12日前に与えられた。ΔV=1.84×10^−2 km/sは、ケースの値より約55%小さい。e=10^−2 57%小さくなるe=10^−3 57.6%小さくなりましたe=10^−4この転送では、値1つの軌道は9.994×10^2 km、e=1.744×10^−1、I=89.5∘近点は825.07km、遠点は1173.7km、操縦時間は42.12日です。
操作を実行する時間m2衝突の21日強前の30.46日であった。ΔV軌道遷移を実行するために使用されたのは≈9.81×10^−3 km/s。操作時、初期軌道は近点860.0 kmで、初期値から4.44%の変化でした。1つの等しい1.0×10^3 km、e=1.399×10^−1、I=89.9∘遠点高度は1140.0kmで、当初の値より約4%高い。
ΔVこの操作で使用されたものは、m2以前のケースと比較してm2以前の症例で行われたこの操作では、ΔV71.5%と71.4%低いe=10^−4そしてe=10^−3それぞれ、
e=10^−2この差は66.4%小さくなりました。
最後の作戦(m3)のためにe=10^−1最も小さい値を持っていたΔV分析されたすべてのケースに関連して発見された、≈1.19×10^−3 km/s。離心率が高いため、中心天体との衝突は積分後数日以内に起こるため、操作は数日以内に実行されます。この場合、移行は軌道継続期間のわずか11.53日で発生しました。この操作を実行するために、次の初期条件が考慮されました。a=9.998×10^2 km、e=1.048×10^−1、I=89.5∘、遠点高度は895.0 km、遠点高度は1104.0 kmです。前述のように、この操作は、ある楕円軌道から別の楕円軌道への移動コストが最も低い操作です。e=10^−4、この操作にはΔV95%小さくなるe=10^−3この割合は95.3%で、94.8%はe=10^−2。


図6:軌道操作による燃費分析(ΔV/t)生涯の関係と比較。(ΔV/t)分析されたすべてのケースについて。a) 分析されたケース
e=10^−4b) ケーススタディe=10^−2初期条件:a=1000 km、I=90∘、ω=0∘そしてΩ=0∘。
2つの操作を行うmP与えるΔVの5.48×10^−2 km/sで寿命は100日強。2回の操縦を行うm3与えるだろう
ΔVの2.38×10^−3 km/sの場合≈23 日。この作戦のコストmPよりもはるかに高いm3、以来ΔV数日間の命を賭けた作戦で使用されたものは23倍も小さい。
mP別の作戦で、今度はm2この場合、m3より経済的でもあります。2つの操作を実行するにはm2、ΔV見つかったのは≈1.962×10^−2 km/sで60日をわずかに上回る寿命を達成します。この値は、ΔV2つの作戦のm3したがって、最善の策はe=10^−1はm3。
このセクションで説明した結果は、2 つの共平面楕円軌道を伴う操作を実行するための最適な条件を示すために不可欠でした。シミュレーションでは、最も経済的な操作は、軌道要素の変動をほとんど伴わずに実行される操作であることが示されました。これらの要素の変動と操作時間の関係を示す図では、これらの操作が最も実行可能であることは明らかです。
このセクションで示した結果から得られるもう一つの重要な事実は、コストの低いマヌーバは離心率が次の値に等しい最終軌道に対するマヌーバであるということ。
10^−2そして10^−1これらの値で最終軌道に到達するために実行された操作は、e低い値を示したΔV最終軌道で行われた他の操作と比較してe等しい10^−4そして
10^−3最終目的地がe=10^−1値を示したΔV他の値で実行された操作よりも最大95%低いe分析された。さらに、最終軌道への操作は、e=10^−3そしてe=10^−4非常に近いΔVしたがって、最終軌道への移行は、e=10^−3この離心率の軌道の寿命はより長く、離心率の低い軌道では約45日長くなります。
e=10^−4このセクションで説明する操作を実行する際に使用されるすべてのパラメータを表3に示します。
表3:の価値ΔVおよび操作を実行する際に使用される初期条件mP、m1、m2そしてm3離心の最終値e=10^−1そしてmP、m1、m2、m3、m4そしてm5のためにe=10^−2、
e=10^−3そしてe=10^−4。𝐓𝐦操作が行われた時間であり、𝐓𝐜衝突時間です。

ある作戦が他の作戦と比べてどれだけ経済的であるかを示す別の方法は、
ΔV操作を実行するために1日あたりに費やされる(ΔV/t)寿命の関数として。この分析は、次のような過去の研究で示されている。フェレイラ2022自然衛星の周りで宇宙船の軌道操作を行うためのより良いポイントを見つける。たとえば、図6 は離心率のいくつかの値に対する寿命の関数としてこの関係を示しています。
図6は、軌道の位置を修正するために1日あたりに必要な燃料の量を示しています。この図には、ΔV/tただし、この値の実現可能性を寿命日数の関数として分析する必要があります。
図6aでは、e=10^−4、最良の値は20~100日の範囲で見つかります。25日では、最小値は2.47×10^−6 km/(s.day)が見つかります。この時点で、ΔVは6.19×10^−5
km/s。このような操作を12回行えば、すでに操作と同じ寿命を達成できます。
mP衝突の1日前に実行され、最小限の燃料消費で済みます。
この場合、e=10^−3、軌道の持続時間が長くなり、軌道要素の変化が遅くなります。したがって、最小ΔV/t値は25~150日の範囲、より正確には95日の範囲にあります。1.37×10^−7 km/(s.day)は、ΔVの1.31×10^−5 km/s、前の場合と同様に、どちらが最良かΔV
寿命の観点で。この値を持つ操作を数回行うだけで、寿命が大幅に延びます。
図6bに示した分析では、e=10^−2の最小値はΔV/t数日間の積分で見られる。離心率が高いため、ΔV/t5日から40日程度です。20日では値が最小になります。
5.76×10^−6 km/(s.day)。この時点で、ΔVは1.15×10^−4 km/s。ΔV操縦のために発見されたmP衝突の数日前に行われたΔV
図6bの強調された点に関連して、衝突の数日前に操作を実行するよりも、最小値で複数の操作を実行する方がはるかに実現可能です。
1.15×10^−4 km/sで、軌道の継続時間を達成しますmP、燃料消費量が大幅に削減されます。
のためにe=10^−1この図から、ΔV/tは、前の場合と同様に動作します。見つかった最小値は1.82×10^−5 km/(s.day)、5日間の積分で。関連する
ΔVは9.11×10^−5 km/sで、この場合も最高ですΔVこの場合の値。
4 近点論を修正するための操作
ω最近、ザビエル2022;フェレイラ2022;タミス2022近点引数がゼロ以外の値であることを示す研究を発表した(ω)と昇交点の経度(Ω) は軌道の寿命を延ばすために不可欠である。これらの研究では、(ω) そして (Ω)軌道寿命を延ばすことができる。チネリ2019;張2019近点引数の変化を修正するための操作モデルが提案されています。これらの操作は、この角度が最も長い軌道寿命の領域で見られる値に近いままになり、軌道の持続時間を延長することを保証するため、不可欠です。
宇宙船の打ち上げ時に考慮される初期パラメータによっては、近点引数が目的の地理的位置に配置されない場合があり、そのため修正が必要になります。
図7は楕円を角度だけ回転させる様子を示している。
θ、これはまた、ω。

図7:楕円軌道の角度による回転θ。θはまた、ω操作中に修正される値。近点引数を値で変更したい場合θ半径を変えずにaそしてその奇抜さ
e、この操作は軌道面内で実行されなければならない。このような操作の実現は次のように表される。シディ1997:

どこa半長軸である。e偏心度はθ近点引数の望ましい変化は、Pは、初期軌道と操作後の軌道の共通点であり、ΔV軌道に加算される総速度は修正する
ωただし、式19は定数の場合にのみ有効であることに注意することが重要です。aそしてeこれらのパラメータの値が高い場合には効果がなくなります。
上記を踏まえると、ΔV近点引数の変動のいくつかのケースについて計算する。式19を効果的に使用するには、ΔV軌道長半径と離心率の変化が小さい期間にわたって計算されます。この研究で分析したケースでは、近点引数修正操作を実行するのに最適な時期は50日以内であり、それ以降は近点引数と離心率が大幅に変化します。チネリ2019。 したがって、ΔV50日以内の時点で計算され、最終的な望ましい軌道は前のセクションで分析したのと同じ離心率の値を持つことになります(ef=10^−4、10^−3、10^−2、10^−1)。
最終離心率が10^−4、a=1000 キロメートル、i=90∘、 そしてω=Ω=0∘、軌道長半径は積分全体を通じて約1kmの小さな変化を被ります。しかし、離心率は約80日で増加し、その後50日で軌道操作が実行されます。軌道がこの寿命に達すると、そのパラメータは軌道長半径です。
9.997×10^2 キロメートル、e=9.7×10^−4、θ=2.32×10^2度(近点引数の変化)。これらのパラメータを考慮すると、ΔVの1.92×10^−3km/s が得られます。
のためにef=10^−3、その他の初期条件は、e=10^−4
この場合、軌道長半径も約1kmとわずかに変化します。離心率は積分100日目頃まで非常に低いままですが、近点引数は大きく変化するため、50日目に軌道操作が行われます。50日目の軌道長半径は9.99×10^2km、離心率8.6×10^−4、 そしてθ8.0度に等しい。したがって、ΔV軌道上のこの点は5.85×10^−5km/s。前のセクションでは、最も実行可能な操作は、e等しい10^−3この離心率を持つ軌道は寿命が長く、長期間にわたって要素の変化が少ないままである。これはここでも示されている。ΔV=5.85×10^−5km/s は、このような操作ではかなり大きな値です。
操作を実行するための最適な間隔はef=10^−2 20日間です。この間、軌道の長半径は9.99×10^2km、離心率1.23×10^−2、θ22度に等しいので、ΔV=2.29×10^−3
km/s。初期パラメータは、前のケースで使用したものと同じです。
の場合ef=10^−1初期離心率は非常に高いため、機動実行に最適な間隔は最大8日間です。この間隔内の長半径と離心率は初期値からほとんど変化せず、ほぼ一定のままです。したがって、この間隔内の任意のポイントの値は、式19で使用して、目的の軌道を計算することができます。
ΔV例えば、8日間の積分では、半長軸は9.99×10^2kmの場合、離心率は1.0×10^−1、θ=1.8∘、そしてしたがってΔV必要なのは6.68×10^−3km/秒。
このセクションで提示された結果は、近点引数を修正するための操作の実現可能性を示しています。
ΔVs異なる離心率で見つかった結果から、最も実行可能な操作は、e等しい10^−3この場合の値は、10^−5km/sです。この場合、およそ0.058m/s 修正のみ1∘
近点引数の変動。
さらに、前のセクションで示したように、軌道の持続時間が短い場合に操作を実行すると、より効果的であることが示されました。
このセクションの議論全体の要約を表4に示す。
表4:の価値ΔV近点引数の変動を修正するための操作を実行する際に使用される初期条件(θ=ω)。 どこTm操作を実行する時間であり、
ef意図した最終軌道の公転性です。

宇宙探査機のチタニア周回軌道操作
2024年12月29日
抽象的な
ほとんどの宇宙ミッションでは、探査機がミッションターゲットの周囲にかなり長い時間留まることが興味深い。ミッションの寿命が長いほど、周回する物体に関する情報収集の機会が増える。この研究では、宇宙探査機がチタニアの表面と衝突するのを回避する方法を示すことを目的とした軌道操作を紹介する。重力ポテンシャルを2次まで拡張することで、係数による重力場の非対称性が明らかになる。
C22チタニアの帯状係数J2
、および天王星の重力摂動が検討されている。共面バイインパルス操作の 2 つのモデルが提示されている。最初の操作は、最初の楕円軌道を最終的な円軌道に移行するもので、2 つ目の操作は、最初の楕円軌道をやはり楕円である最終的な軌道に移行することを目的とする。操作を実行する前に、軌道の傾斜角と半長軸の遅れが調査される。操作を実行するための最良のシナリオを指摘するために、移行を行うことができる軌道上のさまざまなポイントについての研究が提示されている。さらに、近点引数の変動を修正するための操作戦略が提示されている。結果は、統合の数日後に実行される操作が、衝突の数日前に実行される操作よりも経済的であることを示しています。操作の経済性は、速度の増加と寿命の比率の分析によっても実証されています。
キーワード:軌道、操縦、寿命、天体力学、数値シミュレーション、惑星衛星
1導入
近年、太陽系のガス惑星に宇宙ミッションを送ることへの関心が高まっています。ビブ1NASAとESAは、2024年から2037年にかけて氷の巨星へのミッションを計画している。これらのミッションは、これらのシステムの起源と進化を理解するのに役立つ可能性がある。さらに、いくつかのミッションは、2023年に打ち上げられ、木星とその衛星であるガニメデ、エウロパ、カリストを調査する木星ICy衛星探査機(JUICE)ミッションなど、特定の自然衛星に向けられている。グラッセ2013。
いくつかの研究は、自然衛星の周りのより良い軌道を探しています。これらの研究の目的は、これらの衛星をターゲットとする将来の宇宙ミッションに役立つ重要なデータを提供することです。しかし、探査機を宇宙に送り込むことは、多くの時間と投資を必要とするプロセスです。ミッション中、探査機が観測対象の天体の周りを長期間にわたって周回することが望ましいです。したがって、目的の物体の観測を成功させるには、長期間の軌道を探し、ミッションターゲットとの衝突を回避することが非常に重要です。
作品ザビエル2022氷の巨大惑星である天王星の衛星の一つであるティタニアの周回軌道に関する研究を発表する。著者らは、さまざまな離心率を持つティタニアの周回軌道を調査している。第3の天体による摂動とティタニアの重力係数を考慮し、寿命マップから寿命の長い軌道を見つける。数値シミュレーションの結果、寿命が最も長い軌道は離心率が10^−3
著者らはまた、近点引数と昇交点経度をゼロ以外の値にすると探査機の寿命を延ばすことができることを示している。さらに、ティタニアの重力係数の誤差による寿命感度に関する研究では、離心率が10^−3これらの潜在的なエラーの影響を最も受けます。
長期軌道は、タミス2022この場合、天然衛星は木星のガリレオ衛星の 1 つであるイオです。著者らは、探査機の衝突や脱出の可能性を検出することができました。重要な寿命を持つ軌道は、6 か月から 2.3 年の範囲でした。さらに、この研究では、イオの周りの軌道は摂動源からの距離が短いため、摂動の影響を受けやすいことが示されました。最後に、著者らは、近点引数と昇交点の経度にゼロ以外の値を割り当てることの重要性を強調しました。
によって開発された作品チネリ2022天然衛星エウロパの周囲を低高度かつ高度傾斜の高い軌道で周回する探査機の寿命に関する研究結果が発表されました。その結果、第 3 天体の傾斜角と交点位相が探査機の寿命に影響を与えることが示されました。
自然衛星の周回軌道を長期間研究するには、提案されたミッションターゲットとの探査機の衝突を回避する方法を見つける必要がある。この意味で、チネリ2019、エウロパ周回軌道修正操作が提案されている。その結果、適切な修正操作戦略によって寿命を延ばすことができることが示された。軌道修正操作は、フェレイラ2022著者らは、土星の天然衛星タイタンの周りの長期軌道を分析した後、このような操作を実行するための最良の結果を提示している。
上記を踏まえ、本稿では、探査機がティタニアの表面と衝突するのを回避するための軌道操作のモデルを提示する。最初の操作では、探査機を初期の楕円軌道から最終的な円軌道に移行することを提案する。2 番目のモデルでは、初期の楕円軌道から最終的な楕円軌道への移行であり、両方とも同一平面上にある。この 2 番目のモデルでは、軌道のさまざまなポイントで操作を実行し、操作を衝突の近くで行うか、ミッションの存続期間の 2、3 日以内に行う方が実現可能かどうかを分析した。また、近点引数の小さな変動を修正するための操作モデルも提示する。これらの操作は、半長軸の偏差と離心率が小さいポイントを考慮して実行された。
2 数学モデル
ここで使用されるシステムには、中心天体としてのティタニア、ティタニアの周りを周回する宇宙探査機、そして第3の天体としての天王星が含まれる。天王星はティタニアの周りを半径1.5メートルのケプラー軌道で周回すると想定されている。
25.362×10^3 kmと質量8.68×10^25 kg ( https://ssd.jpl.nasa.gov/ )。数値シミュレーションで使用した軌道要素は表1に示す。また、チタニアの2つの主要な重力項も考慮する。
J2そしてC22、値は1.13×10^−4そして3、38×10^−5
、 それぞれチェン2014これらは、重力場においてケプラー項に次いで最も重要な項である。これらの項は、軌道の離心率や傾斜角など、いくつかの軌道要素に大きな変化をもたらす。このように、これらは物体の不規則な形状をモデル化するのに最も効果的な項となる。ツィルト2009;ツィルト2010;ザビエル2022チタニアの場合、これらの項が文献で利用可能な唯一のものであることは注目に値する。これらの係数に加えて、チタニアの質量(35.27×10^20kg)とその半径(788.9
この研究では、100km以上の距離の探査機が対象とされている。探査機の運動方程式は次のように表される。シーレス2006:

どこP→Tチタニアの重力ポテンシャルの2次までの拡張である。
PTx、PTyそしてPTzの構成要素であるPTベクター。
m宇宙探査機の質量はMTチタニアの質量とMu天王星の質量。
r→そしてr→uはそれぞれ探査機と天王星の半径ベクトルです。
表1:天王星に対するチタニアのパラメータ。
パラメータ 価値
半長径(km) 435.8×10^3
偏心 1.18×10^−3
傾斜(∘) 1.0×10^−1
近点引数(∘) 1.64×10^2
昇交点の経度(∘) 1.67×10^2
平均異常値(∘) 2.05×10^2
JPL ウェブサイト: https://ssd.jpl.nasa.gov/。
まず、軌道は方程式1 - 4で記述されるシステムを考慮して数値的に積分された。これらの数値積分中に、操作が行われた。軌道を積分し、操作を実行するために、マーキュリーパッケージに変更が加えられた。チェンバース1999。
2.1 軌道操作
軌道の減衰過程において、軌道要素は変化する。したがって、軌道操作を行う際には、半長軸(a)、偏心率(e)、傾斜(i)。たとえば、探査機がミッションターゲットの表面に衝突する直前で操作が行われたとします。その場合、軌道の離心率は大きくなり、長半径にかなりの変動が生じる可能性があります。したがって、このセクションでは、2 つの操作モデルを紹介します。最初に、初期の楕円軌道から最終的な円軌道への移行を検討し、その後、宇宙船を初期の楕円軌道から最終的な楕円軌道に移行させて、傾斜角を考慮せずに軌道の元の高度を修正します。両方の操作は共面です。最終軌道はミッションの目的の軌道であり、初期軌道は摂動が作用して初期軌道が変更された後の軌道です。
2.1.1 楕円軌道から円軌道への操縦。
ここで紹介する最初の操作は、宇宙探査機を楕円軌道から最終的な円軌道に移行することです。最初のインパルス(ΔV1)が楕円軌道の遠点に印加され、探査機はトランスファー楕円軌道に入る。2番目のインパルス(ΔV2) は、探査機がトランスファー軌道の遠点にあるときに適用され、探査機が最終的に希望する円軌道を占有するようにする。速度の総増分は、モジュール (ΔV1) そして (ΔV2軌道遷移を実行する時間は、遷移軌道の周期の半分です。この操作を実行するための方程式は次のように記述されます。


どこVap初期軌道の遠点における速度である。
Vp1移行軌道のポイント1における速度、ΔV1最初の衝動V2は移行軌道の遠点(点2)における速度である。
五c私r最終的な円軌道の速度、ΔV2
2番目の衝動とΔ五総衝動。
2.1.2 楕円軌道間の移動
この研究で紹介するもう一つの操縦は、最初の楕円軌道から、同じく楕円である別の最終軌道への操縦である。これらの軌道は共面である。これは、宇宙船の公称軌道が楕円である場合に起こる。この操縦では、最初のインパルス(Δ五1) は、最初の楕円軌道の近点に印加され、その後、探査機はトランスファー軌道に投入される。2 回目のインパルス (Δ五2) がトランスファー軌道の遠点に適用され、宇宙船は最終的な楕円軌道に配置されます。(Δ五1) そして (Δ五2) は、操作を実行するための速度の合計増加分になります。このような操作を実行するための方程式は次のように表されます。

どこrp1そしてra1初期軌道の近点と遠点です。さらに、rta転送楕円の遠点である。
rp2最終軌道の近点である。ra2=rtaは、望ましい最終軌道の遠点である。速度の増加に関しては、
Vp1初期軌道の点1における速度に等しい、Vpt移動楕円の点1における速度、ΔV1最初の衝動Vat
移動楕円の遠点における速度、Va2最終的な目標軌道に関する点2の速度、ΔV2 2番目の衝動とΔV総衝動。
3 結果の分析
最初に提示された結果は、最初の楕円軌道から最終的な円軌道への最初の操作に関するものである。これは、公称軌道が円で、摂動後の軌道が楕円である場合に発生する状況である。次に、最終的な望ましい軌道の半径は、最も長い軌道継続時間を持つ領域に従って選択された。これは、ザビエル2022この半径は1000~2000 kmの範囲で、200 km間隔で変化します。操作を実行する適切なタイミングの選択は次のように行われました。まず、初期の長半径が(ai=Ri)で、この軌道の減衰を分析し、開始位置からの変化が大きな値に達したときに操作を実行します。この点の軌道要素を取得し、それらを初期軌道の要素と見なします(黒い軌道、図1)。軌道の初期条件の小さな変化は、その寿命を短くし、軌道は大きな離心率と傾斜角に達します。したがって、初期位置の大幅な変更後に、傾斜角を無視して軌道を元の高度位置に戻す操作がいくつか実行されます。4つの初期傾斜角が検討されました。60∘、70∘、80∘そして90∘
図1は、操作がどのように実行されるかを示した図です。

図1:望ましい最終的な円軌道の表現。Rf軌道の半径です。紫色はRf=1000 km、緑Rf=1200 km、青はRf=1400 km、赤はRf=1600 km、ライトグリーンRf=1800 kmと濃い紫色Rf=2000 km。初期軌道は黒線で表されます
操縦を計画するために、私たちはチタニアの重力係数を考慮しました。
J2そしてC22、および天王星の重力係数も取得しました。その後、式6~11を利用して、目的の軌道を達成するために必要な操作を実行しました。
初期値の20~30%の最大偏差を持つ軌道(黒い軌道、図1)は、初期傾斜角が
60∘、70∘そして80∘全てのシミュレーションで、軌道が偏差に達すると寿命は240~250日に近づき、
ΔV再び半径1000kmの円軌道に到達するのに必要な距離は約
1×10^−2−6×10^−2 km/s。この傾斜角の軌道の総寿命が 252 日であることを考慮すると、最大の傾斜角の変化は衝突の数日前に発生すると結論付けられます。
初期傾斜角が90∘、最大の変動I最終軌道の5%である。しかし、
ΔV範囲は4×10^−2−1×10^−1 km/sで、減衰時間は1~17日の範囲です。
ΔV半径1000~1200kmの最終軌道に到達するための操作です。これらの軌道では傾斜角の変化率が最も高くなります。
長半径の変化は非常に小さく、初期値の0.1~0.9%の間です。分析された4つの傾斜については、
60∘、70∘、80∘そして90∘、半径の最大変化が0.6 - 0.9 %になるケースがあります。これらのケースでは、ΔV範囲は8×10^−2−1.1×10^−1 km/s。最も低い値を示したケースはΔV最終軌道は半径1000~1200kmです。
いくつかのミッションでは、宇宙船の位置が大きく変化する前に、短い寿命で位置を修正することを選択します。たとえば、図2は、最小値を見つけようとする研究を示しています。
ΔV軌道遷移を実行する前に、初期位置が大きく変化する。したがって、ここで注目する操作は、傾斜角または長半径の大きな変化を伴う操作ではない。以前のケースと同様に、分析した4つの傾斜角について、最小ΔV最終軌道の半径が 1000 ~ 2000 km の場合に計算されます。

図2:最小ΔV最終軌道の円半径の関数として。4つの初期傾斜を分析する
60∘、70∘、80∘そして90∘それぞれオレンジ、赤、緑、黒の色です。初期値:ai=Ri=1000−2000 キロメートル、ei=0そしてω=Ω=0∘
予定されている最終軌道の半径は1000−2000 キロ。図2に示すように、Δ五およそ5.4×10^−5
全ての傾斜角において、最終軌道半径1050kmの速度は毎秒1000kmである。
60∘、軌道修正は5日後に実行され、これは約45軌道周期に相当します。その時点で、軌道長半径と離心率は次の値でした。
1.0498×10^3 kmと2.8×10^−4それぞれ、長半径の変化率は0.016初期値の%と0.45傾斜の%。
軌道傾斜角が70∘この作戦は14日後に実行され、1つのそしてeは1.0492×10^3 kmと2.3×10^−4、それぞれである。このΔVは0.4%、長半径については0.01%.
Iのために等しい80∘そして90∘、最小ΔVは5日後に発見される。
I=80∘、操縦の瞬間、半長軸の値は1.0497×10^3 kmと離心率2.0×10^−4傾斜角と長半径の変化は0.36% そして0.02%である。90∘、この操作は、a=1.0497×10^3 kmとe=2.03×10^−4傾斜の変化はおよそ0.3% および半長軸上0.023%。この最小範囲内では、半径950kmの最終軌道の場合、ΔV軌道変更に必要な速度は、他の解析例よりも大きい。初期傾斜角が80∘そして90∘これらの値は5.7×10^−4 km/sの場合I=80∘そして5.55×10^−4 km/sの場合I=90∘。 のためにI=70∘この軌道はΔV=7.1×10^−4 km/秒。
表2:の価値ΔV軌道傾斜角と軌道長半径に大きなオフセット値を持つ軌道変更の場合。軌道傾斜角、軌道継続時間、遠点半径(rapo)、最終円軌道半径(rc私rc)、長半径オフセット(Def a)、傾斜角(Def I)のパーセンテージ、およびそれに相当する
ΔV。

最良の値を分析するためにΔⅤ軌道操作を行うために用いられるいくつかの値を示す表2は、ΔⅤ傾斜角と長半径が遅れている軌道に使用されます。各傾斜角について、I= 60∘、I= 70∘、I= 80∘そしてI= 90∘、の値ΔVおよび操作を実行するための初期条件が提示されています。半径が 1000、1200、1400、1600、1800、および 2000 km の最終軌道のケースが提示されています。
次の議論は、2つの楕円軌道間の操作で得られた結果についてである。ザビエル2022離心率が等しい物体の軌道の減衰は、
10^−4、10^−3、10^−2そして10^−1研究されている。著者らは、軌道離心率が大きいほど寿命が長くなると結論付けた。
10^−3したがって、この研究で調査された最終的な軌道は、その研究で研究された軌道と同じ離心率を持っています(10^−4、10^−3、10^−2そして10^−1)。これを偏心と呼ぶ。
ef図3にこれらの軌道を示します。

図3:最終的な楕円軌道の表現。オレンジは離心率10^−1緑は10^−2、ピンク10^−3青は10^−4。
それぞれの偏心に対する操作を実行するために、一連の数値シミュレーションが作成されました。
軌道上の6つのポイントが、各値に対して操作を実行するために選択されました。
e
この選択は、衝突前に複数の操作を異なる時間に行う方が実現可能か、それとも周回機が衛星に衝突する直前に1回だけ操作を行う方が実現可能かを分析することを目的としています。このような操作は𝐦𝐏、𝐦𝟏、𝐦𝟐、𝐦𝟑、𝐦𝟒そして𝐦𝟓。 いる
メートル
P、この操作が主な操作である理由は、この操作がティタニアの表面に最も近い地点、つまり衝突に最も近い地点で実行されるためです。この操作のおおよその近点は、すべての値で790 kmです。
e
. 操縦のポイントm5
ティタニアの表面から最も遠く、数日間の減衰で操作が実行される。
mp. の近点はm5約965kmです。m1、m2、m3、 そしてm4演習は中間地点で行われるmpそしてm5の近点はm1約825kmです。
m2≈860 キロメートル、m3≈895 キロメートル、m4≈930 kmとm5≈965 km。ポイントは35kmごとに変わります。
すべてのシミュレーションは以下を考慮して行われた。
a=1000 キロメートル、
I=90∘、ω=Ω=0∘、重力係数
J2そしてC22チタニアと天王星の重力の影響。
最初の一連の操作は、e=10^−4、総寿命は268.536日となる。軌道操作で考慮されるすべてのポイントは、図4(上部)に示されている。操作を実行する際のいくつかのパラメータの変化を関連付けるために、図4(下部)は、近点の位置(rp)、eそしてI時間の関数として。この図では、各操作が実行された日も視覚化できます。


図4:実行された6回の軌道位置の投影(mP、m1、m2、m3、m4そしてm5) のためにe=10^−4(上部)軌道要素の変化e、i
、および寿命と操縦時間の関数としての近点半径(下部)。初期条件:a=1000 キロメートル、
e=10^−4、i=90∘、ω=Ω=0∘。メイン作戦 mPパラメータは次のとおりです。a=9.993×10^2 km、e=2.094×10^−1、i=87.9∘
、近点は790.0 km、遠点は1208.59 km、軌道変更時間は267.26日です。これらの値を考慮すると、近点は約21%、傾斜角は2.3%、長半径は0.1%減少します。離心率も3桁増加しています。
mP衝突の約1日前に操縦が行われた。推定
ΔVこの移転は≈5.26×10^−2 km/s。この操作の位置は、図4の赤い点線で示されています。
2番目の操作(m1)、 のためにe=10^−4は、衝突の約 8 日前に、数値積分の 259.87 日以内に実行されました。この選択された時点で、軌道の近点は 825.09 km で、初期値の約 17.5% でした。その他の初期条件は次のとおりです。
a=9.989×10^2 km、e=1.740×10^−1、i=88.3∘
、遠点高度は1172.88kmである。この操作を実行するには、ΔV使用されたのは約4.34×10^−2 km/s。この軌道要素の変化を分析すると、259.87日間で近点が約180km減少し、傾斜角が1.4∘軌道半径は2km拡大した。m1図4では青い点線で表されます。
この操作(m2)は、衝突の約19日前、248.59日後に実行されました。この操作では、ΔV離心率の軌道に到達するのに必要な10^−4だった
3.45×10^−2 km/s。操作を実行するために次の初期条件が使用されました。a=9.991×10^2 キロメートル、e=1.392×10^−1、i=88.5∘
、近点は 860.01 km、遠点は 1138.35 km です。軌道の減少中に軌道要素のすべての変化の中で最も変化率が高いのは近点です。近点はほぼ 14% 減少しました。軌道長半径と軌道傾斜角はそれぞれ 0.1% と 1.66% 減少しました。離心率の場合は、初期値から 3 桁増加しました。図4のオレンジ色の線は、この操作を表しています。
図4では、操作を表す色(m3) のためにe=10^−4緑色で表示されます。この操作の有効期間は234.86日で、衝突の約33日前でした。この操作では、近点距離は初期値の999.9kmから895kmまで約10%減少しました。離心率は2桁増加し、e=9.970×10^−2、遠点高度は103km近く上昇した。長半径と傾斜角はそれぞれ0.1%と1.22%と小さな変化であった。
m3以前の軌道要素のオフセットは小さいが、その操作が行われる地点はミッションにとって興味深いものであり、ΔV必要なのは2.56×10^−2 km/秒。
(m4)は、図4で水色で示されており、マヌーバ実行に要した時間は218.20日であった。マヌーバは衝突の50.34日前に行われ、その近点は930.16kmで、初期値と比較して約7%低下した。傾斜に関しては、変化は小さく、約1.33%であった。
6.95×10^−2そしてΔVの1.70×10^−2 同じ原点位置に到達するために km/s が使用されました。
ピンク色の最後の動きe=10^−4図4に示すのは、軌道が187.84 すでに述べたように、この操作は他の操作よりもミッション開始からより短い日数で実行されるため、近点の減衰はより小さくなります。この点の初期条件はa=9.991×10^2 km、e=3.420×10^−2、I=89∘、近点は965.01km、遠点は1033.37kmである。近点オフセットは≈3.5%そしてその傾向≈1.11%速度増加を伴うΔV=8.31×10^−3 km/秒。
実行されたすべての操作を比較すると、e=10^−4、最善の策は(m5)。ΔVの8.31×10^−3 km/sは、生存日数に対してはるかに小さい。他の操縦と比較すると、(mP)例えば、2つの操作(m5)が実行されると、軌道の寿命は最大374日となり、2×ΔV等しい1.662×10^−2 km/s。2つの操作(mP)、私たちは一生≈534 日ですが合計ΔVの1.052×10^−1 km/s、総速度の約6倍ΔV(で使用されるm5)。もし、操縦のポイントで6回の操縦を行えば(m5) 、寿命が長くなり、燃料消費量が少なくなります。この比較は他の操作にも当てはまります。
以下の議論は計算のためのものであるΔ五のためにe=10^−3結果は、e=10^−4
、操作ポイントの投影図は省略します。前回と同様に、操作を実行するために軌道上の 6 つのポイントが選択されました。この場合、軌道継続時間は 313 日でした。
のm1この操作は衝突の 8.56 日前に 304.44 日間にわたって行われた。この操作では、近点は初期値より 17.4% 小さい 825.18 km、遠点は減衰前の値より約 15% 大きい 1157 km とされた。その他の初期条件は以下のとおりである。
a=9.999×10^2 km、e=1.747×10^−1、I=87.9∘の価値ΔVおよそ4.33×10^−2 km/sの値を比較するとΔV見つかったm1前の場合、値が非常に近く、違いは無関係であることがわかります。
機動用m2我々は、衝突の約18日前の295.15日の操縦時間という初期条件を使用しました。a=9.996×10^2 km 、e=1.396×10^−1、I=88.0∘
、近点は860.10km、遠点は1139.22kmです。パラメータの変化に関しては、近点では約14%、傾斜角では2.2%の減少がありました。これらの初期条件で、
Δ五の≈3.43×10^−2 km/s。前回の演習と同様に、ΔVのためにm2に非常に近いΔV同じ操作がケースで分析されたe=10^−4。
でm3、ΔVV見つかったのは2.54×10^−2 衝突の30.96日前の282.04日の間に、軌道は秒速kmで回転した。この時点で、軌道の長半径は
9.990×10^2 km、離心率1.041×10^−1、傾斜は88.2∘近点変動は10.4%、遠点変動は10.2%近く増加した。m3分析された値と類似の値も持っている
e=10^−4。 のためにm4、の値ΔV見つかったのは≈1.68×10^−2 264.93日間、毎秒キロメートルの速度で飛行した。これらの軌道変更では、近点の減少はほぼ7%、傾斜角は≈1.5% 近点は930.03 km、遠点は1069.74 km、離心率は6.986×10^−2同じ操作を分析すると、10^−4の値はΔV近づいています。
軌道遷移の初期条件はm5検討されたのは:a=9.989×10^2 km、e=3.388×10^−2、I=88.9∘、近点965.05km、遠点1032.76kmであった。結果は、ΔV=8.01×10^−3 km/s、減衰≈3.4%近点から≈1.22%傾斜角と寿命は234.19日で、衝突の約79日前です。
同様の分析を実施し、e=10^−4、今回はm5そしてm1、我々は、この操作に注目するm5最も実現可能な方法です。
m5過ごした8.01×10^−3 生後234日目に操縦を行うには、m1過ごした4.33×10^−2 304.44日間の人生でkm/s。2回の操縦を行えばm5探査機は468.38日間軌道上に留まり、合計ΔVの1.602×10^−2 km/s。2回の操縦の場合m1、合計ΔVだろう8.66×10^−2 608日強の寿命で毎秒キロメートルの速度で走行し、これはΔV 2つの操作に使用されるm5。
グラフで見ると、e=10^−2これらは、e=10^−1については後ほど紹介しますが、ここでは省略します。e=10^−2、その作戦mPは、ΔVの4.99×10^−2 km/sの値と比較するとΔVのためにmPの場合e等しい10^−4そして10^−3この値はわずかに低く、5%この操作では、近点オフセットは 20.2% で、傾斜角はわずか 0.6% でした。使用されたその他の初期条件は次のとおりです。a=9.988×10^2 km、e=2.089×10^−1、I=89.4∘ 遠点高度は 1207.00 km です。この操作は 152.68 日、つまり中心天体との衝突の 0.5 日前に発生しました。
の場合m1、機動時間は衝突のほぼ7日前(145.90日)であり、近点(825.01km)で約17%、傾斜角で1.2%減少しました。
ΔV転送を実行するために必要なのは≈4.10×10^−2 km/s。半径は9.995×10^2 km、離心率は1.745×10^−1遠点高度は1174.00kmである。
m1 また、同じ近点に対して、以前のケースで分析された操作よりもわずかに低い値(約 5%)を示しています。
所要時間はm2 135.00日、数値積分終了の18日前でした。この操作を実行するには、ΔVの≈2.92×10^−2 km/sが見つかりました。
ΔVケースについてe=10^−4そしてe=10^−3、ΔV今では約15%小さくなっています。当初の楕円軌道はa=9.991×10^2 km、e=1.389×10^−1
、i=89.6∘、近点は860.26 km(≈13%初期値より小さい)、遠点高度は1137.90 km(≈13%初期値より大きい)。
作戦のためにm3衝突の約 30 日前に実行された軌道の初期条件は次のとおりです。a=9.989×10^2 km、e=1.039×10^−1、I=89.5∘、近点は895.07kmで、ほぼ9%の減少で、遠点は1102.80kmで、初期値より約93km増加しました。速度の総衝撃は≈2.31×10^−2 km/sです。この値は、ΔV症例で発見e=10^−4そしてe=10^−3。
水色で表された操作は、m4 104.85日で起こった。速度の増加を見つけるにはΔVこの時点で、6%の変化を伴う近点が考慮された。傾斜角は約0.3%、操縦の瞬間まで。これらの初期条件では、長半径は9.993×10^2 km、e=6.931×10^−2、i=89.7∘、近点は930.07km、遠点は1068.6kmで、ΔVの1.45×10^−2 km/sという値が見つかりました。この値は、m4以前のケースでは。
最後の作戦、m5、 のためにe=10^−2は、生後74.11日後に実施されました。初期条件は次のとおりです。
a=9.999×10^2 キロメートル、e=3.482×10^−2、i=89.8∘、近点は965.14kmで2.5%の減衰、遠点は1034.7kmである。この場合、ΔVだった6.04×10^−3 km/秒。
離心率のある最終軌道に向けて実行されるすべての操作において10^−2、ΔV同じ操作で得られた値よりも低い値を示した。e=10^−4そしてe=10^−3パーセンテージで言えば、mP≈5%、m1≈5%、m2≈15%、m3≈9%、m4 15%から17%の間m5 25%から27%小さくなるe=10^−2以前のケースと比較して。
機動m5再び、これが最も良い作戦として発見された。ここでは、この作戦をm2 2つの操作を行うm5軌道寿命は約148日で、合計ΔVの1.208×10^−2 km/s。しかし、2回の操縦を行うとm2、軌道の寿命は合計270日になりますΔVの6.38×10^−2 km/sです。寿命はm2、ΔVのためにm5約5.2倍小さくなります。


図5:実行された4つの操作の軌道位置の投影(mP、m1、m2そしてm3) のために
e=10^−1(上部)軌道要素の変化eそしてI寿命と操縦時間の関数としての近点半径(下部)。初期条件:
a=1000 km、e=10^−1、i=90∘、ω=Ω=0∘シミュレーション時間は52日間です。
最後に、図5に、以下の操作の結果を示します。e=10^−1この場合、我々は4つの操作のみを考慮する。
mP、m1、m2、 そしてm3この選択は、軌道の初期近点が990kmから始まるため、操縦のためのポイントが
m4(近点距離は930km)とm5(近点距離は965km)は不可能です。色と点は、前の場合と同じです。
mPにm3この場合、合計統合時間は 52 日でした。
のmP軌道修正は、近点790km、遠点1209.5kmを考慮して行われた。9.998×10^2 km、e=2.098×10^−1そして
I=89.5∘総インパルス2.74×10^−2 km/sは衝突のほぼ1日前に与えられた。操縦の時点で、近点オフセットは約12.2%、傾斜角は0.55%であった。
ΔV分析されたmP前の例では、見つかった値は、e=10^−2、ほぼ48%小さくなりますe=10^−3そしてe=10^−4。
の場合m1速度の増加は衝突の約8日前、42.12日前に与えられた。ΔV=1.84×10^−2 km/sは、ケースの値より約55%小さい。e=10^−2 57%小さくなるe=10^−3 57.6%小さくなりましたe=10^−4この転送では、値1つの軌道は9.994×10^2 km、e=1.744×10^−1、I=89.5∘近点は825.07km、遠点は1173.7km、操縦時間は42.12日です。
操作を実行する時間m2衝突の21日強前の30.46日であった。ΔV軌道遷移を実行するために使用されたのは≈9.81×10^−3 km/s。操作時、初期軌道は近点860.0 kmで、初期値から4.44%の変化でした。1つの等しい1.0×10^3 km、e=1.399×10^−1、I=89.9∘遠点高度は1140.0kmで、当初の値より約4%高い。
ΔVこの操作で使用されたものは、m2以前のケースと比較してm2以前の症例で行われたこの操作では、ΔV71.5%と71.4%低いe=10^−4そしてe=10^−3それぞれ、
e=10^−2この差は66.4%小さくなりました。
最後の作戦(m3)のためにe=10^−1最も小さい値を持っていたΔV分析されたすべてのケースに関連して発見された、≈1.19×10^−3 km/s。離心率が高いため、中心天体との衝突は積分後数日以内に起こるため、操作は数日以内に実行されます。この場合、移行は軌道継続期間のわずか11.53日で発生しました。この操作を実行するために、次の初期条件が考慮されました。a=9.998×10^2 km、e=1.048×10^−1、I=89.5∘、遠点高度は895.0 km、遠点高度は1104.0 kmです。前述のように、この操作は、ある楕円軌道から別の楕円軌道への移動コストが最も低い操作です。e=10^−4、この操作にはΔV95%小さくなるe=10^−3この割合は95.3%で、94.8%はe=10^−2。


図6:軌道操作による燃費分析(ΔV/t)生涯の関係と比較。(ΔV/t)分析されたすべてのケースについて。a) 分析されたケース
e=10^−4b) ケーススタディe=10^−2初期条件:a=1000 km、I=90∘、ω=0∘そしてΩ=0∘。
2つの操作を行うmP与えるΔVの5.48×10^−2 km/sで寿命は100日強。2回の操縦を行うm3与えるだろう
ΔVの2.38×10^−3 km/sの場合≈23 日。この作戦のコストmPよりもはるかに高いm3、以来ΔV数日間の命を賭けた作戦で使用されたものは23倍も小さい。
mP別の作戦で、今度はm2この場合、m3より経済的でもあります。2つの操作を実行するにはm2、ΔV見つかったのは≈1.962×10^−2 km/sで60日をわずかに上回る寿命を達成します。この値は、ΔV2つの作戦のm3したがって、最善の策はe=10^−1はm3。
このセクションで説明した結果は、2 つの共平面楕円軌道を伴う操作を実行するための最適な条件を示すために不可欠でした。シミュレーションでは、最も経済的な操作は、軌道要素の変動をほとんど伴わずに実行される操作であることが示されました。これらの要素の変動と操作時間の関係を示す図では、これらの操作が最も実行可能であることは明らかです。
このセクションで示した結果から得られるもう一つの重要な事実は、コストの低いマヌーバは離心率が次の値に等しい最終軌道に対するマヌーバであるということ。
10^−2そして10^−1これらの値で最終軌道に到達するために実行された操作は、e低い値を示したΔV最終軌道で行われた他の操作と比較してe等しい10^−4そして
10^−3最終目的地がe=10^−1値を示したΔV他の値で実行された操作よりも最大95%低いe分析された。さらに、最終軌道への操作は、e=10^−3そしてe=10^−4非常に近いΔVしたがって、最終軌道への移行は、e=10^−3この離心率の軌道の寿命はより長く、離心率の低い軌道では約45日長くなります。
e=10^−4このセクションで説明する操作を実行する際に使用されるすべてのパラメータを表3に示します。
表3:の価値ΔVおよび操作を実行する際に使用される初期条件mP、m1、m2そしてm3離心の最終値e=10^−1そしてmP、m1、m2、m3、m4そしてm5のためにe=10^−2、
e=10^−3そしてe=10^−4。𝐓𝐦操作が行われた時間であり、𝐓𝐜衝突時間です。

ある作戦が他の作戦と比べてどれだけ経済的であるかを示す別の方法は、
ΔV操作を実行するために1日あたりに費やされる(ΔV/t)寿命の関数として。この分析は、次のような過去の研究で示されている。フェレイラ2022自然衛星の周りで宇宙船の軌道操作を行うためのより良いポイントを見つける。たとえば、図6 は離心率のいくつかの値に対する寿命の関数としてこの関係を示しています。
図6は、軌道の位置を修正するために1日あたりに必要な燃料の量を示しています。この図には、ΔV/tただし、この値の実現可能性を寿命日数の関数として分析する必要があります。
図6aでは、e=10^−4、最良の値は20~100日の範囲で見つかります。25日では、最小値は2.47×10^−6 km/(s.day)が見つかります。この時点で、ΔVは6.19×10^−5
km/s。このような操作を12回行えば、すでに操作と同じ寿命を達成できます。
mP衝突の1日前に実行され、最小限の燃料消費で済みます。
この場合、e=10^−3、軌道の持続時間が長くなり、軌道要素の変化が遅くなります。したがって、最小ΔV/t値は25~150日の範囲、より正確には95日の範囲にあります。1.37×10^−7 km/(s.day)は、ΔVの1.31×10^−5 km/s、前の場合と同様に、どちらが最良かΔV
寿命の観点で。この値を持つ操作を数回行うだけで、寿命が大幅に延びます。
図6bに示した分析では、e=10^−2の最小値はΔV/t数日間の積分で見られる。離心率が高いため、ΔV/t5日から40日程度です。20日では値が最小になります。
5.76×10^−6 km/(s.day)。この時点で、ΔVは1.15×10^−4 km/s。ΔV操縦のために発見されたmP衝突の数日前に行われたΔV
図6bの強調された点に関連して、衝突の数日前に操作を実行するよりも、最小値で複数の操作を実行する方がはるかに実現可能です。
1.15×10^−4 km/sで、軌道の継続時間を達成しますmP、燃料消費量が大幅に削減されます。
のためにe=10^−1この図から、ΔV/tは、前の場合と同様に動作します。見つかった最小値は1.82×10^−5 km/(s.day)、5日間の積分で。関連する
ΔVは9.11×10^−5 km/sで、この場合も最高ですΔVこの場合の値。
4 近点論を修正するための操作
ω最近、ザビエル2022;フェレイラ2022;タミス2022近点引数がゼロ以外の値であることを示す研究を発表した(ω)と昇交点の経度(Ω) は軌道の寿命を延ばすために不可欠である。これらの研究では、(ω) そして (Ω)軌道寿命を延ばすことができる。チネリ2019;張2019近点引数の変化を修正するための操作モデルが提案されています。これらの操作は、この角度が最も長い軌道寿命の領域で見られる値に近いままになり、軌道の持続時間を延長することを保証するため、不可欠です。
宇宙船の打ち上げ時に考慮される初期パラメータによっては、近点引数が目的の地理的位置に配置されない場合があり、そのため修正が必要になります。
図7は楕円を角度だけ回転させる様子を示している。
θ、これはまた、ω。

図7:楕円軌道の角度による回転θ。θはまた、ω操作中に修正される値。近点引数を値で変更したい場合θ半径を変えずにaそしてその奇抜さ
e、この操作は軌道面内で実行されなければならない。このような操作の実現は次のように表される。シディ1997:

どこa半長軸である。e偏心度はθ近点引数の望ましい変化は、Pは、初期軌道と操作後の軌道の共通点であり、ΔV軌道に加算される総速度は修正する
ωただし、式19は定数の場合にのみ有効であることに注意することが重要です。aそしてeこれらのパラメータの値が高い場合には効果がなくなります。
上記を踏まえると、ΔV近点引数の変動のいくつかのケースについて計算する。式19を効果的に使用するには、ΔV軌道長半径と離心率の変化が小さい期間にわたって計算されます。この研究で分析したケースでは、近点引数修正操作を実行するのに最適な時期は50日以内であり、それ以降は近点引数と離心率が大幅に変化します。チネリ2019。 したがって、ΔV50日以内の時点で計算され、最終的な望ましい軌道は前のセクションで分析したのと同じ離心率の値を持つことになります(ef=10^−4、10^−3、10^−2、10^−1)。
最終離心率が10^−4、a=1000 キロメートル、i=90∘、 そしてω=Ω=0∘、軌道長半径は積分全体を通じて約1kmの小さな変化を被ります。しかし、離心率は約80日で増加し、その後50日で軌道操作が実行されます。軌道がこの寿命に達すると、そのパラメータは軌道長半径です。
9.997×10^2 キロメートル、e=9.7×10^−4、θ=2.32×10^2度(近点引数の変化)。これらのパラメータを考慮すると、ΔVの1.92×10^−3km/s が得られます。
のためにef=10^−3、その他の初期条件は、e=10^−4
この場合、軌道長半径も約1kmとわずかに変化します。離心率は積分100日目頃まで非常に低いままですが、近点引数は大きく変化するため、50日目に軌道操作が行われます。50日目の軌道長半径は9.99×10^2km、離心率8.6×10^−4、 そしてθ8.0度に等しい。したがって、ΔV軌道上のこの点は5.85×10^−5km/s。前のセクションでは、最も実行可能な操作は、e等しい10^−3この離心率を持つ軌道は寿命が長く、長期間にわたって要素の変化が少ないままである。これはここでも示されている。ΔV=5.85×10^−5km/s は、このような操作ではかなり大きな値です。
操作を実行するための最適な間隔はef=10^−2 20日間です。この間、軌道の長半径は9.99×10^2km、離心率1.23×10^−2、θ22度に等しいので、ΔV=2.29×10^−3
km/s。初期パラメータは、前のケースで使用したものと同じです。
の場合ef=10^−1初期離心率は非常に高いため、機動実行に最適な間隔は最大8日間です。この間隔内の長半径と離心率は初期値からほとんど変化せず、ほぼ一定のままです。したがって、この間隔内の任意のポイントの値は、式19で使用して、目的の軌道を計算することができます。
ΔV例えば、8日間の積分では、半長軸は9.99×10^2kmの場合、離心率は1.0×10^−1、θ=1.8∘、そしてしたがってΔV必要なのは6.68×10^−3km/秒。
このセクションで提示された結果は、近点引数を修正するための操作の実現可能性を示しています。
ΔVs異なる離心率で見つかった結果から、最も実行可能な操作は、e等しい10^−3この場合の値は、10^−5km/sです。この場合、およそ0.058m/s 修正のみ1∘
近点引数の変動。
さらに、前のセクションで示したように、軌道の持続時間が短い場合に操作を実行すると、より効果的であることが示されました。
このセクションの議論全体の要約を表4に示す。
表4:の価値ΔV近点引数の変動を修正するための操作を実行する際に使用される初期条件(θ=ω)。 どこTm操作を実行する時間であり、
ef意図した最終軌道の公転性です。

図8は、最も良い値の一つである操縦の表現を示しています。
ΔV、初期軌道(黒線)、移行楕円(赤線)、および望ましい最終楕円軌道(緑)。この操作を実行するための値は、表3と図の説明に記載されています。

図8:最小値を用いた操作の表現
ΔV等しい8.01×10^−3初期条件:a=9.989×10^2km、ei=3.388×10^−2、i=88.9∘。
5最終コメント
この研究では、高傾斜角に対する軌道操作の研究を紹介します。どの軌道が軌道継続時間中により大きな変化を与えるかを調べるために、4つの初期傾斜角を考慮します。
60∘、70∘、80∘そして90∘最終軌道半径は1000~2000kmとなる。
我々の結果は、初期傾斜角が70∘他の傾斜よりも大きな偏向を示した。また、1000~1050 kmのより小さな軌道半径で最良の操作が見つかったことも観察した。最小
ΔVの5.4×10^−05 すべての傾斜に対して km/s。
また、最終離心率が10^−4、10^−3、10^−2、 そして10^−1
軌道上のいくつかの点について、ある操作の実現可能性を他の操作と比較します。
e=10^−4、e=10^−3、 そしてe=10^−2、そして3点e=10^−1。
この一連のシミュレーションは、事故発生から数日以内に実施される操縦が、衝突直前に実施される操縦よりも経済的であることを示した。これらの結果は、
ΔV/tこの比率は、軌道の持続期間が数日の場合、操作時間あたりの速度が実際に低くなり、その結果、軌道要素の変動が小さくなることを示しています。
最後に、近点変動の議論を修正できる操作のオプションを提示する。
ΔV関心のあるポイントで。私たちの結果は、統合後数日以内に実行される操作が衝突の近くで実行される操作よりも実行可能であることを示す以前の結果を裏付けています。
ΔV、初期軌道(黒線)、移行楕円(赤線)、および望ましい最終楕円軌道(緑)。この操作を実行するための値は、表3と図の説明に記載されています。

図8:最小値を用いた操作の表現
ΔV等しい8.01×10^−3初期条件:a=9.989×10^2km、ei=3.388×10^−2、i=88.9∘。
5最終コメント
この研究では、高傾斜角に対する軌道操作の研究を紹介します。どの軌道が軌道継続時間中により大きな変化を与えるかを調べるために、4つの初期傾斜角を考慮します。
60∘、70∘、80∘そして90∘最終軌道半径は1000~2000kmとなる。
我々の結果は、初期傾斜角が70∘他の傾斜よりも大きな偏向を示した。また、1000~1050 kmのより小さな軌道半径で最良の操作が見つかったことも観察した。最小
ΔVの5.4×10^−05 すべての傾斜に対して km/s。
また、最終離心率が10^−4、10^−3、10^−2、 そして10^−1
軌道上のいくつかの点について、ある操作の実現可能性を他の操作と比較します。
e=10^−4、e=10^−3、 そしてe=10^−2、そして3点e=10^−1。
この一連のシミュレーションは、事故発生から数日以内に実施される操縦が、衝突直前に実施される操縦よりも経済的であることを示した。これらの結果は、
ΔV/tこの比率は、軌道の持続期間が数日の場合、操作時間あたりの速度が実際に低くなり、その結果、軌道要素の変動が小さくなることを示しています。
最後に、近点変動の議論を修正できる操作のオプションを提示する。
ΔV関心のあるポイントで。私たちの結果は、統合後数日以内に実行される操作が衝突の近くで実行される操作よりも実行可能であることを示す以前の結果を裏付けています。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます