
ガリレオ衛星のエウロパの氷の厚さは不明だけど多重リング盆地の形成のシミュレーションから20㎞を超える必要があると出た。30㎞レベルなのか100㎞超えなのかはエウロパクリッパー待ちです。以下、機械翻訳。クレジット:Brandon Johnson generated with the assistance of AI.
多重リング盆地の形成がエウロパの氷殻の厚さを制限する
要約
木星の衛星エウロパには、厚さ不確かな氷の殻の下に海が存在します。エウロパには、いくつかの同心円状のリングを示す 2 つのマルチリング盆地があります。これらの多重リング盆地の形成は、氷殻の厚さと熱構造の影響を受けやすいと考えられています。ここでは、エウロパへの衝突で形成される多重環盆地をシミュレーションし、観察された環構造を再現するには総厚さ 20 キロメートルを超える氷の殻が必要であることを発見しました。薄い氷の殻(厚さ 15 キロメートル未満)は、観察されたリング構造と矛盾する圧縮テクトニクスをもたらします。私たちのシミュレーションは氷の殻の熱構造にも敏感であり、エウロパの少なくとも20キロメートルの氷の殻が、温かい対流する氷を覆う厚さ6〜8キロメートルの導電性の蓋で構成されていることを示しています。この研究から生じるエウロパの氷の殻構造に対する制約は、エウロパの潜在的な居住可能性についての我々の理解に直接関係している。
導入
エウロパには地下海洋があるという強力な証拠があります。エウロパの氷殻の厚さは、わずか数キロメートルの厚さから数十キロメートルの厚さ までと推定されています。エウロパの氷殻の厚さは、さまざまな表面特徴の形成メカニズムを制約し、氷殻内で起こるプロセスを決定します。氷の殻の厚さは、氷の殻内の潮汐加熱の程度 と、地表と海洋の間でどのように交換が起こるかも決定します。これらはどちらもエウロパの潜在的な居住可能性を理解する上で重要です 。
エウロパのクレーターは、氷の殻の構造を制約する重要な方法であると長い間考えられてきました。衝突により最初に一時的なクレーターが掘削され、このクレーターが重力によって崩壊し、衝突後のクレーターの形態が形成されます。私たちが今日観察している形態は、他の衝撃後のプロセスによって緩和と修正を経験している可能性があることに注意してください。いくつかのヨーロッパのクレーター内に中央の山が存在することは、衝突によって氷の殻全体が溶けなかったことが示唆され、氷の殻の厚さが少なくとも 3 ~ 4 km であることを示唆しています。エウロパのクレーターの深さの直径の傾向は、直径が約 8 km を超えるクレーターは、小さいクレーターよりも浅くなることを示しています。クレーター形成のシミュレーションは、一時的なクレーターの崩壊が深さの弱い層の影響を受けるという解釈を支持し、氷殻の導電性部分の厚さが約 7 km であることを示唆しています。しかし、これらのシミュレーションでは、上部の導電性氷の蓋の下にある、温かい対流氷で構成される弱い層と液体の水とを区別することができませんでした。多重環構造への遷移が深さで同様のレオロジー遷移を示し、このレオロジー遷移が氷と海の境界面に対応すると仮定すると、エウロパの氷の殻全体の厚さは 19 ~ 25 km になるでしょう。
カラニッシュとタイヤは、中心からほぼ 100 km まで延びるいくつかの同心円状の環状地溝を示すヴァルハラ型の多重環状盆地です。これらの多重リング盆地は、クレーターの縁内の中央盆地領域と、縁を越えた内輪領域と外輪領域の 3 つの領域で構成されています。地溝、溝状の特徴は、一対の正反対の正断層 によって生成され、外側のリング領域のリングを構成します。盆地リングは、一時的なクレーターの崩壊が、強いリソスフェアの下にある弱い物質の流れによって吸収されるときに形成されます。内向きの流れはリソスフェアを引き込み、伸長と正断層の形成を引き起こします。リソスフェアが十分に薄い場合、いくつかの同心の地溝が形成されると予想されます。したがって、多重リング盆地形成はターゲットの熱機械構造に敏感であり、エウロパ上の多重リング盆地形成のシミュレーションは、その氷殻の厚さと熱構造についての洞察を提供することができます。私たちは、iSALE-2D 衝撃物理コード ( 29 – 31 ) を使用して、エウロパ上のマルチリング盆地の形成をシミュレートしました。私たちは、メッシュ空間解像度 50 m で秒速 15 km でエウロパのような目標に衝突する半径 1.0 ~ 1.8 km の衝突体を検討しました。我々は、5~10 kmの導電性蓋に相当する34.60~17.31 K/kmのリソスフェア温度勾配で、10~50 kmの厚さの氷殻をテストしました。シミュレーションの主な制約として、観測された地溝 に基づく半径方向のひずみを使用しました。半径方向のひずみは、地溝によって受け入れられる拡張の大きさを表し、盆地の外側からその中心に向かう地溝の半径方向の変位を累積することによって計算されます。私たちのモデル設定と材料パラメーターは以前の研究 と一致しています。衛星の多環盆地形成のシミュレーションを動機として、ひずみに対する指数関数的な依存性を持つ損傷モデル と、ひずみの局在化を強化して断層のような挙動を引き起こす可能性があるダイラタンシー モデル も組み込みました。詳細については、「材料と方法」を参照してください。
結果
厚い氷殻の上に形成された多重リング盆地
私たちの基準モデルは、厚さ 6 km の導電性蓋と総厚さ 20 km の氷の殻を持つターゲットに 15 km/s で衝突する半径 1.5 km のインパクタです。6 km の導電性蓋は、熱伝導率が 3 W m^-1 K^-1 であると仮定すると、86 mW/m 2の熱流に相当することに注意してください。エウロパへの推定平均衝突速度は 26 km/s ですが、クレーターのスケーリングの法則は、26 km/s では、15 km/s で衝突する衝突体の 0.7 倍小さい衝突体が同じサイズの過渡現象を生成することを示唆しています。クレーターとなり、同様の盆地形態が形成されます。まず、クレーター崩壊のダイナミクスと、発生する総塑性ひずみに焦点を当てます。iSALE の断層は、個別の滑り面ではなく、局所的な全塑性ひずみの領域として現れます。衝撃により衝撃波が発生し、その後すぐに希薄化または解放波が発生します。これらの波の通過により物質が動き始め、深さ 19 km の一時的なクレーターが掘削されます (図 1Aおよび図 S1A)。一時的なクレーターは重力によって崩壊し、中央に大きな隆起が生じます(図1Bおよび図S1B)。中央の隆起が崩壊するにつれて、盆地中心から離れた物質は依然として内側に移動しており、盆地に向かう方向と遠ざかる方向の両方を切る小規模な正断層が形成されています(図1Cおよび図S1C)。中央隆起の崩壊により別の空洞が形成され、さらに空洞が崩壊し、より多くの内向きの流れが生じます。氷の内向きの流れの大部分は、表面から深さ約 8 km の弱い物質によって吸収され、盆地の中心から 50 km を超える深さの物質の内向きの流れのほとんどは、内向き崩壊の第 2 段階で発生します (図 1Dおよび図 1D)。図S1D)。崩壊の第 2 段階では、崩壊の第 1 段階で生じた正断層のひずみが 4 ~ 5 倍に増加します (図 1、C および D、図 S1、C、D)。2000 秒後、クレーターは最終状態に落ち着きます (図 S2A)。タイヤとカラニッシュの周囲で観察されたリングを構成する断層 (図 S3) と比較して、私たちのシミュレーションでは、より小さなオフセットを持つより多くの正規断層が生成されます (図 S4 を参照)。より低い解像度でのテストは、より高い解像度を考慮するとひずみの局在化が強化されることを示唆しています。ひずみの局在化を強化するレオロジーを考慮すると 、より大きなオフセットを持つ少数の断層にひずみが局在化する可能性が高くなります。しかし、断層の様式とこれらの断層によって適応される全ひずみは観測結果と一致しています。
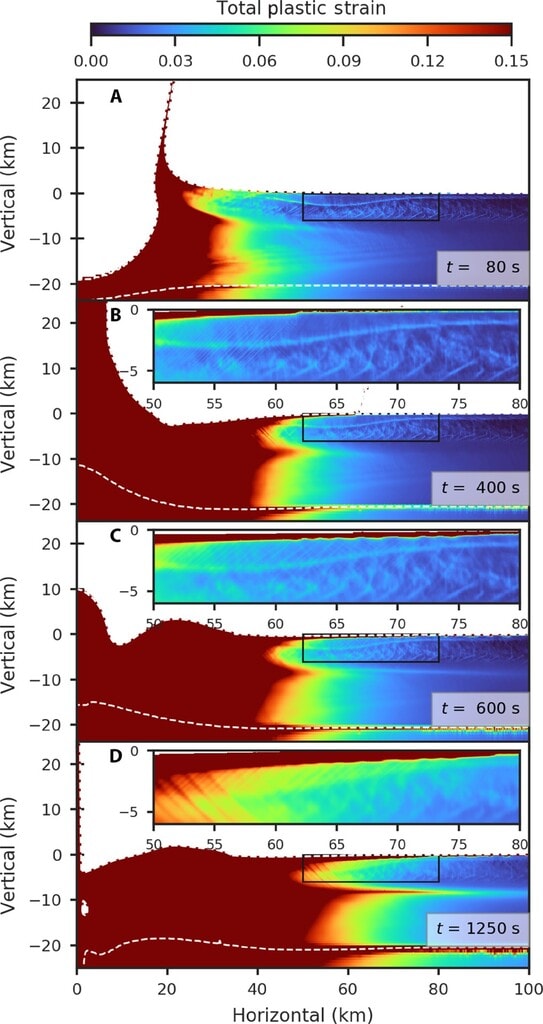
図1。氷のマルチリング盆地の形成に関する基準モデルの時系列。
シミュレーションは、厚さ6kmの導電性蓋を持つ厚さ20kmの氷殻に半径1.5kmの衝突体を衝突させるものである。材料は総塑性ひずみに応じて色付けされます。白い破線の曲線は、マテリアルの境界 (つまり、氷の殻と海洋) を示します。挿入図は、導電性の氷の蓋の上部 6 km と地溝が形成される盆地の外側部分の拡大図です。図 S1 は総塑性ひずみを対数スケールで示し、図 S1 は総塑性ひずみを示します。S4 は 600 秒の地溝の位置を示しています。ムービーS1はこの図をアニメーション化したものです。( A ) は一時的なクレーターの形成を示し、 ( B ) は中央隆起の形成を示し、 ( C ) は断層の形成を示し、 ( D ) は崩壊の二次段階での断層の強化を示します (主要な部分を参照)詳細についてはテキストを参照してください)。
観測された断層オフセット からの半径方向ひずみの推定により、地溝が発生する盆地の中心から 30 ~ 100 km の領域でモデルと観測を定量的に比較することができます (図 S3)。トレーサー粒子の半径方向の変位を追跡することにより、モデルの半径方向のひずみを計算します (材料と方法)。厚さ 20 km および 30 km の氷殻のシミュレーションでは、観察された放射状ひずみがよく再現されています (図 2A )。厚さ 20 km および 30 km の氷殻の半径方向のひずみは、カラニッシュで測定された最大ひずみ 0.6 ~ 1.2% の範囲内で 40 km で 0.8% です (図 2A )。タイヤはカラニッシュよりも大きく、盆地の中心から 40 km では半径方向の最大ひずみが 1.0 ~ 1.5% 大きくなります (図 3B を参照)。盆地の中心 (または任意の場所) から 40 km の位置で観測的に導出されたひずみ推定値は、その表面が元の位置から盆地の中心に向かって内側に移動することによってその場所で経験した半径方向のひずみの総量を表すことに注意してください。このひずみを決定するには、その点の外側のすべての断層に沿ったオフセットを追加する必要があります ( 21、22 )。タイヤとカラニッシュで観察されたように、純粋な伸長テクトニクスの場合、半径方向のひずみは盆地の中心に向かって移動するにつれて単調増加します。厚さ8km、10km、および15kmの氷殻シミュレーションでは、盆地の中心に向かって移動するにつれて半径方向のひずみは単調増加しません(図2B )。半径方向のひずみの局所的な減少は、中央の隆起が崩壊して材料を外側に押すときに発生する圧縮塑性ひずみと推力断層を表しています (図 S5 および S6)。したがって、15 km より薄い氷の殻は、観察された盆地の外輪と一致しません。Melosh と McKinnon ( 24 ) は、リソスフェアの下にある弱いアセノスフェアが流動的すぎる場合、クレーター底の振動によって外向きの波が生成され、その結果、放射状および同心円状の破壊が生じると予測したことに注目します。私たちのシミュレーションは、リングテクトニクス理論を広く検証しています アセノスフェアが弱すぎる場合にはヴァルハラ型多環盆地は生成されないという結論を含む。厚さ 20 ~ 50 km の氷殻の場合、氷殻の厚さが増加するにつれて盆地中心から 40 km の半径方向のひずみが減少することを除いて、結果は同様です。この類似性は、氷の多環盆地の形成において海洋が限定的な役割を果たしていることを示唆しています。さらに、現在の観測上の制約では、厚さ 20 ~ 50 km の氷殻はカラニッシュで観測された放射状ひずみを再現することができ、これらの盆地が氷殻の厚さの下限制約を提供するだけであることを示唆しています。しかし、ヴァルハラ型のマルチリング盆地では、クレーターの崩壊時に容易に流れることができる、暖かく弱い氷の上に重なる比較的薄い導電性の氷の殻が必要です。この熱構造は、暖かい内部と地下海洋を備えた氷の天体で発生する可能性が高いため、ヴァルハラ型多重環盆地形成における海洋の役割が限られているにもかかわらず、ヴァルハラ型多重環盆地と海洋世界とのつながりが依然として期待されています。
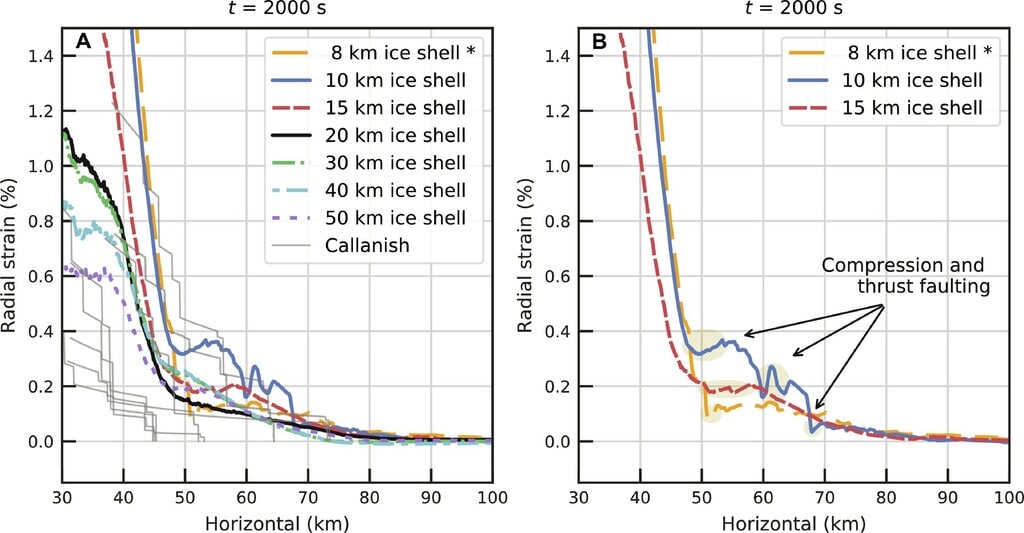
図2。半径方向のひずみに対する氷殻の厚さの影響。
半径方向のひずみは、初期深さ 1 km で計算されます (詳細は「材料と方法」を参照)。初期深さの選択は結果にほとんど影響を与えません (図 S11A)。( A ) カラニッシュの観測結果と比較した、インパクタ半径 1.5 km のシミュレーションによる半径方向ひずみ。それぞれの太い色の線は、異なる氷殻の厚さでのシミュレーションの結果を示しています (凡例を参照)。(A) の細い灰色の線は、カラニッシュ ( 21、22 )で観測された断層オフセットから決定された、さまざまな方位角での半径方向のひずみプロファイルです。8 km の氷の殻には導電性の蓋しか含まれていないことに注意してください。他のすべてのシミュレーションには、対流する氷を覆う厚さ 6 km の導電性蓋が含まれます。( B ) の影付きの領域は、圧縮断層と推力断層の領域を表します。

図3。導電性蓋の厚さとインパクタ半径が半径方向のひずみに及ぼす影響。
図 2と同じ図ですが、厚さ 20 km の氷殻上のさまざまな導電性蓋の厚さ (蓋導電性) と衝突子の半径 ( r imp ) を示しています (凡例を参照)。( A ) は、観測的に導出されたカラニッシュの半径方向ひずみと比較した半径 1.5 km のインパクタを使用したシミュレーション結果を示し、( B ) は、観測的に導出されたタイヤの半径方向ひずみと比較した、半径 1.8 km のインパクタを使用したシミュレーション結果を示します。(A) の細い灰色の線は、カラニッシュで観察された断層オフセットから決定された異なる方位角での半径方向のひずみプロファイルであり、(B) ではタイヤについてのそれです ( 21、22 )。
インパクターのサイズと導電性蓋の厚さは半径方向のひずみに影響します
氷殻の厚さ以外に、シミュレーションを最も制御できるパラメーターは、インパクターのサイズと氷殻の熱構造です。まず、厚さ 6 km の導電性蓋を使用したシミュレーションにおけるインパクタ サイズの影響について説明します。半径 1.0 km の衝突体によって生成される半径方向のひずみは、観察された盆地リングを説明するには小さすぎるため (図 4 )、シミュレーションでは明らかな断層は発生しません (図 S7)。厚さ 10 km の氷殻上の半径 1.2 km の衝突体の最終的な半径方向のひずみには明確な圧縮ゾーンはありませんが (図 4A )、中央隆起の崩壊中に衝上断層が発生していることがわかります (図 4A)。 .S8)、これは観察と一致しません。半径 1.2 km の衝突体が厚さ 20 km または 30 km の氷の殻に衝突すると、カラニッシュに適切に適合する放射状のひずみが生じます。ただし、厚さ 20 ~ 30 km の氷殻に対する、より大きな半径 1.5 km の衝突子のシミュレーションを推奨します。これにより、半径 1.2 km の衝突子よりもわずかに大きな半径方向のひずみと盆地中心からさらに広がる非ゼロの半径方向のひずみが生成されます。シミュレーション (図 4、B および C )。増大した放射状ひずみと断層の横方向の範囲は、盆地の中心から最大 75 km まで広がるカラニッシュの観察された環とより一致しています。20 kmの氷殻上のより大きな半径1.8 kmの衝突体はより大きな半径方向のひずみをもたらしますが、シミュレーションでは観測と一致しない圧縮も示されています(図4B)。したがって、一般に、インパクターのサイズを大きくすると、結果として生じる半径方向のひずみの大きさと横方向の広がりが増加し、それに応じてリングが盆地の中心からさらに離れて形成されることがわかります。しかし、衝突体のサイズが大きすぎると、その後の大きな中央隆起の崩壊によって氷の殻が外側に押し出され、観測と矛盾する位置に圧縮特徴が生じる可能性があります(図4)。
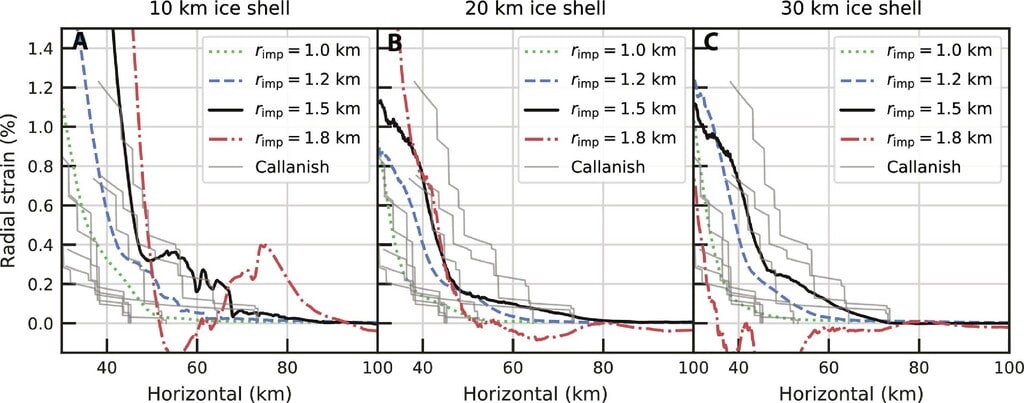
図4。インパクターの半径と氷殻の厚さが半径方向のひずみに及ぼす影響。
図 2と同じ図ですが、10 ~ 30 km の氷殻ケースの衝突半径 ( r imp ) を示しています。( A ) は厚さ 10 km の氷殻、( B ) 厚さ 20 km の氷殻、( C ) は厚さ 30 km の氷殻のシミュレーション結果を示しています。細い灰色の線は、カラニッシュの観測された断層オフセットから決定された、異なる方位角での放射状ひずみプロファイルです ( 21、22 )。すべてのシミュレーションは、対流する氷の上に厚さ 6 km の導電性蓋があることを前提としています。
氷殻の熱構造の影響を分離するために、衝突体の半径と氷殻の厚さをそれぞれ 1.5 km と 20 km に固定したまま、導電性の蓋の厚さの影響について議論します。厚さ 5 km の導電性の蓋を考慮すると、氷の殻が弱すぎるため、中央隆起の崩壊によってリングが観察される領域に強い圧縮が生じ、これは観察と矛盾します。しかし、265 Kで対流する氷の上にある厚さ6〜7 kmの導電性の氷の蓋は、観測されたカラニッシュ井戸の放射状ひずみを再現します(図3A )。これは、より小さなクレーターの形態に基づいて、 Silber と Johnsonによって発見された好ましい熱構造と一致しています。導電性の蓋が厚すぎ(≧8 km)、氷の殻が強すぎる場合、盆地の中心から約45 kmの内側に強い圧縮領域が発生します(図3A)。タイヤまたはカラニッシュの外輪領域には明確な圧縮特徴が観察されないため、これらのモデルは好ましくありません (図 S3)。さらに、これらの厚い導電性蓋の場合、リング形成と一致する局所的な特徴は見られません(図S9)。これらのより強力な氷殻の場合、中央隆起の崩壊は、厚さ 6 km の導電性蓋の場合のように単純に伸びの大きさを減少させるのではなく、盆地の中心近く (40 km の内側) で圧縮を引き起こします。これは、より厚い導電性蓋がリング形成を引き起こさないにもかかわらず、これらのモデルが盆地の中心から 40 km の外側で同様の半径方向のひずみをどのように維持するかを説明します。したがって、我々は、局所的なリング状の特徴を生成し、より小さなヨーロッパのクレーターの形態を再現するために必要な熱構造の以前の推定と一致する、6 km の導電性蓋を好みます ( 17 )。
私たちのシミュレーションは、エウロパの氷の殻が、暖かい対流する下層の上にある導電性の蓋で構成されていることを示唆しています。シルバーとジョンソン は、海洋上の完全に導電性の氷の殻も、エウロパのクレーターの深さと直径の比率の推移を説明できると示唆しました。しかし、厚さ 8 km の純粋な導電性の氷殻 (その下に海がある) への衝撃のシミュレーションでは、10 km および 15 km の氷殻の場合と同様の圧縮ひずみと推力断層が発生します。半径方向のひずみの減少は、圧縮領域を示しています (図 2B )。したがって、私たちのシミュレーションは、カラニッシュの場合、厚さ 20 km 以上で、暖かい対流する氷の上に厚さ 6 km の導電性氷の蓋で構成される氷の殻を明らかに支持しています。対流温度の選択も、多重リング盆地の形成に別の影響を与えます。対流温度が 255 K と低いため、対流副層内の降伏強度が大きくなります (図 S10)。その結果、対流温度が低くなり、内向きの流れが減少し、半径方向の歪みが減少します(図S11C)。入力パラメータの選択における小さな不確実性によって結果が影響を受けないことを確認するために、他の多くのパラメータを調査しました。損傷した材料の摩擦係数と最大ダイラタンシー係数を除いて、変更したパラメータのほとんどは結果にわずかな影響を与えます(補足資料および図S11およびS12)。
より大きなインパクターとより厚いタイヤ用導電性リッド
推定相当直径は 38 km で、タイヤはカラニッシュ [直径33 km ] より若干大きいです。さらに、タイヤ周囲の地溝の観察から推定された半径方向のひずみは、カラニッシュの場合よりも高い半径方向のひずみを意味します。これらのより大きな半径方向のひずみは、基準シミュレーションの半径 1.5 km と比較して、半径 1.8 km のより大きな衝突子の結果であることがわかります。厚さ 6 km の導電性蓋上の半径 1.8 km のインパクターは圧縮を示しますが (図 3A)、厚さ 8 km の導電性蓋上の半径 1.8 km のインパクターは、観察されたタイヤウェルの半径方向の歪みを再現しました (図 3A )。図3B)。このシミュレーションでは、局所的なリング状構造も形成されます (図 S13)。これは、同じ厚さ 8 km の導電性蓋を備えた半径 1.5 km のインパクターの場合には見られません (図 S9)。タイヤ (厚さ 8 km の導電性蓋) とカラニッシュ (厚さ 6 km の導電性蓋) に最適な導電性蓋の厚さのわずかな違いは、エウロパの熱流の空間的または時間的変化の結果である可能性があります。厚さ 7 km の導電性蓋は両方のケースに限界適合を生成するため、タイヤとキャラニッシュの導電性蓋の厚さが同様である可能性を排除できないことに注意してください。半径 1.8 km のインパクターを使用した実験で導電性の蓋が厚くなる (9 km 以上) と、盆地の中心近くで圧縮が発生します (図 3B )。繰り返しますが、これは地溝帯に圧縮の形態学的兆候が見つからないという観察結果と矛盾しています [( 21 , 22 )、考察も参照]。これらの傾向は、半径 1.5 km の衝突体で見られる傾向と類似しています (図 3Aおよび4B )。全体として、厚さ 8 km の導電性蓋を備えた厚さ 20 km 以上の氷の殻に衝突する半径 1.8 km の衝突体が、タイヤに最適なモデルです。
議論
私たちのシミュレーションは、観測されたエウロパの多重リング盆地の構造を再現するには、暖かい対流下層を覆う導電性の蓋で構成される厚さ 20 km を超える氷の殻が必要であることを示しています。また、衝突後の構造や、将来の宇宙船ミッションで観測される可能性のある、それに関連する氷殻の海洋隆起も考慮することができます。私たちの薄い氷の殻(10 kmと15 km)の場合、氷と海の境界面に大きな隆起が見られます(図S5DとS6D)。等静性を通じて、この隆起は、観測されたよりも深い、深さ 0.5 km の盆地を生成します [<0.1 km]。この隆起は、盆地が現在の地形に一致するように粘弾性的に緩和する必要があります。対照的に、20 kmの氷殻ケースでは、氷と海の境界面の隆起はほとんどありません(図S2)。マルチリング盆地の形成に必要な氷殻の暖かく弱い部分の効率的な内向きの流れにより、衝突後にほとんど乱れのない最終的な氷殻の厚さが得られます。これにより、地形が無視できる最終的なクレーター底が形成されます。したがって、最も適切なモデルでは、観察された地形と一致するために、衝撃後の粘弾性緩和を制限する必要があります。いずれの場合も、盆地の中心には融解プールが含まれており(図S2B)、厚い氷の殻の場合でも、表面と海洋の間で交換が起こる可能性があります。
私たちの結果は、インパクターのサイズとリソスフェアの厚さの間にはある程度のトレードオフがあることを示しています。私たちは、より厚いリソスフェアを伴うより大きな衝突体と、より薄いリソスフェアへの小さな衝突が同様の結果を生み出す可能性があることを発見しました(図3)。また、衝突体が大きくなると、一般に半径方向のひずみが大きくなり、盆地の中心からさらに離れたところにリングが形成されることもわかりました。この結果は、盆地リングの範囲は一時的なクレーターのサイズに比例するが、リソスフェアの厚さに反比例するというMelosh によって提唱されたスケーリング とほぼ一致しています。しかし、衝突体が大きすぎる場合、では考慮されていなかった中央隆起の崩壊により、広い圧縮領域が生じることがわかります (図 4 )。したがって、スケーリング は注意して使用する必要があります。
我々は、伸張テクトニクス(地溝)が観察される多重環盆地の外輪領域に焦点を当てており、半径方向のひずみに対して定量的な制約を与えています。タイヤとカラニッシュの内輪領域には、環状の山塊/尾根が存在します。山塊や尾根は通常、圧縮テクトニクスを暗示していることに言及する必要があります。しかし、タイヤとカラニッシュの内側の尾根は、破壊または伸張によって形成された傾斜したブロックのように見えます。これまでの研究では、での暫定的な提案を除いて、圧縮の結果として内側の隆起が生じるという仮説を立てていません。それにもかかわらず、内部領域に明白でない、または不可解な圧縮が存在する可能性を排除することはできません。より厚い導電性蓋を使用したシミュレーションでは、盆地の中心から 30 ~ 40 km で半径方向のひずみが減少しており、これは圧縮テクトニクスを示しています (図 3A では導電性蓋の厚さが 7 ~ 10 km、導電性蓋が 8 ~ 10 km)図3Bの厚さ)。これらの同じシミュレーションには、外輪領域での観察と一致する拡張特徴と半径方向のひずみが含まれています。したがって、内側のリング領域が圧縮を示している場合、20 km より厚い氷殻を使用したシミュレーションにより、内側のリング領域の圧縮と外側のリング領域の拡張を説明できます。対照的に、薄い氷の殻では、逆の構造パターンが発生します。薄氷シェルのシミュレーションでは、盆地から 30 ~ 40 km で伸長とそれを超えると圧縮が示され (図 2B )、これは観測結果と一致しません。
エウロパの氷殻の厚さの横方向の変化は、地球規模で限定されていると考えられています。したがって、ある場所の氷の殻の厚さをヨーロッパ全体に推定するのは合理的です。ただし、エウロパの氷の殻の厚さは時間の経過とともに大幅に変化する可能性があることが示唆されています 。エウロパの平均表面年齢はわずか 20 ~ 200 Ma であると推定されています が、タイヤとカラニッシュの両方が同様の年齢である可能性は低いです。タイヤは、厚さ 8 km のわずかに厚い導電性の蓋を備えたターゲットに衝撃を与えると最適であることがわかりました。これは、エウロパの熱流の空間的または時間的変化を示している可能性があります。しかし、どちらの盆地も、形成時に約 20 km より厚い氷の殻が必要です。これは、一時的な厚さの変化によって、現代において氷殻の厚さが 20 km 以下に減少する可能性は低いことを示唆しています。厚さが 20 km を超える氷の殻は、対流する下層 ( 44 )上の導電性の蓋で構成されている必要があります。これは、対流氷層の上に導電性の氷の蓋を持つ最小シェル厚さ 20 km に関する制約と一致します。厚さ 20 km の氷殻は、クレーターが浅くなり、多重リング構造を示す直径に基づく推定値とも一致します [氷殻の厚さは 19 ~ 25 km。シェンク ]。しかし、私たちの研究は、氷のマルチリング盆地の形成が、その上に形成される氷の殻の最小厚さに制約を与えることを示唆しています。したがって、で示唆されているように、エウロパの氷の殻は 20 km より厚い可能性があり、ガニメデとカリストの氷の殻は 80 ~ 105 km よりかなり厚い可能性があります。
材料と方法
数値的手法
エウロパの多重リング盆地形成を調べるために、iSALE-2D 衝撃物理コード を使用して衝突シミュレーションを実行します。iSALE コードは、惑星の衝突とクレーターをモデル化するために開発され、さまざまな状態方程式と強度モデル を含めることによって SALE コード から改良されました。球形の氷の衝突体が、地下海の上にある氷の殻からなる平らな標的に衝突すると仮定します。氷のマテリアルには Tillotson 状態方程式 (EOS) を使用し、水の海洋には ANEOS を使用します 。衝突体のサイズは半径 1.0 ~ 1.8 km の範囲にあり、これは木星系彗星のサイズの上限に相当します。ターゲットとインパクターに同じ EOS を使用するため、それらの密度は温度と圧力に依存します。それらの参照密度は 910 kg/m^3 です。我々は、Bray の強度モデル パラメーター を使用します。これは、無傷の氷 と損傷した氷の実験室測定に適合します。適度に斜めの衝撃の影響を近似するために、軸対称シミュレーションの衝撃速度は、斜めの衝撃の垂直成分であるとみなされることがよくあります。私たちが選択した 15 km/s は、約 35°の衝突角度での 26 km/s の斜め衝突速度の垂直成分に相当します。15 km/s での垂直衝撃のシミュレーションも計算コストを削減し、以前の研究との一貫性を維持します。我々は異なる衝突体のサイズを調査するだけですが、衝突速度の変動も結果に同様の影響を与えるでしょう。マルチリング盆地内の地溝を解決するには、50 m の解像度を使用します [iSALE の高解像度ゾーンのドメイン サイズは、水平 (半径) 方向に 100 km、垂直方向に 5 km です]。計算メッシュ領域は、結果に影響を与える可能性のある反射を防ぐのに十分な大きさであることに注意してください (iSALE の拡張ゾーンは、水平方向で最大 ~800 km、垂直方向で約 -400 ~ ~140 km をカバーします)。
エウロパの氷殻の厚さを自由パラメータとして扱い、厚さ 8、10、15、20、30、40、50 km の氷殻への衝突をシミュレートします。ターゲットの表面温度は 100 K であると仮定します。ターゲット内の温度プロファイルは、盆地形成の主な制御の 1つです。基準ケースとして、温度 265 K の対流下層上の厚さ 6 km の導電性氷の蓋で構成される氷殻を検討します。導電性氷蓋内の温度勾配は 28.85 K/km です。これは、エウロパの小さなクレーターの深さと直径の比を説明できる氷殻構造の 1 つです。温度プロファイルの影響をテストするために、厚さ 6 km の導電性蓋を備えた基準ケースから導電性蓋の厚さを 5 ~ 10 km の範囲で変化させました。また、対流温度が 255 K、導電性の蓋の厚さが 6 km のターゲットも検討します。これも、より小さなクレーターの形態を再現することがわかっています 。また、厚さ 8 km の完全に導電性の氷殻への衝突もシミュレーションしました。これにより、ヨーロッパのより小さなクレーターの形態も説明できます 。以前の研究に基づいて、シミュレーションに粘弾塑性氷レオロジーを含め、に続くダイラタンシー モデルを含めます。材料の入力パラメータを表 S1 にまとめます。
観測との一致を評価するために、トレーサ粒子の半径方向の変位を使用して半径方向のひずみを計算します。iSALE シミュレーションのラグランジュ トレーサ 粒子は、クレーター形成中のオイラー グリッドを通る物質の塊の動きを追跡します。表面近くの層の細胞は噴出物の定置によって過度に影響を受ける可能性があるため、最初の深さ約 1 km での半径方向の変位を考慮します。初期深さ (0.5 ~ 1.5 km) の半径方向ひずみへの依存性を調査したところ、シェル内の初期深さの選択は、盆地から 40 km を超える距離での基準ケースの半径方向ひずみプロファイルに影響を及ぼさないことが確認されました。中央(図S11A)。一方、より深い深さ (3.0 km および 4.0 km) での半径方向のひずみを考慮すると、半径方向のひずみは小さくなり、表面で観察される変形を表すものではなくなります。地溝は、タイヤとカラニッシュの盆地中心から水平距離約 40 ~ 80 km の範囲で観察されます (図 S3) 。盆地全体が中程度の解像度で画像化されているため、盆地中心の定義がタイヤにとってより適切であることに注意してください。カラニッシュ盆地の約半分だけが中程度から高解像度で画像化されており、これにより中心のフィットと半径方向のひずみのオフセットに不確実性が生じる可能性があります。Singerらの研究に続いて、は観測の半径方向のひずみを表し、100 km から中心に向かって半径方向の変位を ΣΔ r /( r + ΣΔ r ) として累積します。ここで、 rは半径方向の距離、Δ rは半径方向の距離です。変位; したがって、ΣΔ r は合計の内側への変位を表し、分母 ( r + ΣΔ r ) は初期距離を示します。数値シミュレーションでは、半径方向のひずみを計算するために、指定された初期深さにあるすべてのトレーサー粒子を考慮します。衝撃波の通過は衝突後 50 秒で終了するため、これをその時点のトレーサー粒子の半径方向の距離 [すなわちr ( t = 50)] と見なします。合計の内側への変位は、ΣΔ r = r ( t = 50) − r ( t= 2000)、正の値は内側への変位を示します。トレーサ粒子が受ける総塑性ひずみに関係なく、トレーサ粒子の内側への変位を計算することに注意してください。計算された半径方向ひずみの滑らかな変化は、シミュレーションにおける半径方向ひずみが現実ほど局所的ではないことを示すもう 1 つの指標です。観察された放射状ひずみの変動は、自然変動、またはカラニッシュの場合には利用可能なガリレオ画像を使用して盆地の中心を決定する際の不正確さに起因する可能性があります。したがって、観測によって得られたひずみデータと数値シミュレーションを水平方向に比較します。観察された地溝の幅は 0.4 ~ 4.7 km、深さは 14 ~ 210 m であることに注意してください。これらの深さを解決するには、少なくとも 20 m の解像度が必要です。50 m という分解能は観測された深さを分解するには十分ではありませんが、観測された半径方向のひずみを再現するには十分であることが結果からわかります。
多重リング盆地の形成がエウロパの氷殻の厚さを制限する
要約
木星の衛星エウロパには、厚さ不確かな氷の殻の下に海が存在します。エウロパには、いくつかの同心円状のリングを示す 2 つのマルチリング盆地があります。これらの多重リング盆地の形成は、氷殻の厚さと熱構造の影響を受けやすいと考えられています。ここでは、エウロパへの衝突で形成される多重環盆地をシミュレーションし、観察された環構造を再現するには総厚さ 20 キロメートルを超える氷の殻が必要であることを発見しました。薄い氷の殻(厚さ 15 キロメートル未満)は、観察されたリング構造と矛盾する圧縮テクトニクスをもたらします。私たちのシミュレーションは氷の殻の熱構造にも敏感であり、エウロパの少なくとも20キロメートルの氷の殻が、温かい対流する氷を覆う厚さ6〜8キロメートルの導電性の蓋で構成されていることを示しています。この研究から生じるエウロパの氷の殻構造に対する制約は、エウロパの潜在的な居住可能性についての我々の理解に直接関係している。
導入
エウロパには地下海洋があるという強力な証拠があります。エウロパの氷殻の厚さは、わずか数キロメートルの厚さから数十キロメートルの厚さ までと推定されています。エウロパの氷殻の厚さは、さまざまな表面特徴の形成メカニズムを制約し、氷殻内で起こるプロセスを決定します。氷の殻の厚さは、氷の殻内の潮汐加熱の程度 と、地表と海洋の間でどのように交換が起こるかも決定します。これらはどちらもエウロパの潜在的な居住可能性を理解する上で重要です 。
エウロパのクレーターは、氷の殻の構造を制約する重要な方法であると長い間考えられてきました。衝突により最初に一時的なクレーターが掘削され、このクレーターが重力によって崩壊し、衝突後のクレーターの形態が形成されます。私たちが今日観察している形態は、他の衝撃後のプロセスによって緩和と修正を経験している可能性があることに注意してください。いくつかのヨーロッパのクレーター内に中央の山が存在することは、衝突によって氷の殻全体が溶けなかったことが示唆され、氷の殻の厚さが少なくとも 3 ~ 4 km であることを示唆しています。エウロパのクレーターの深さの直径の傾向は、直径が約 8 km を超えるクレーターは、小さいクレーターよりも浅くなることを示しています。クレーター形成のシミュレーションは、一時的なクレーターの崩壊が深さの弱い層の影響を受けるという解釈を支持し、氷殻の導電性部分の厚さが約 7 km であることを示唆しています。しかし、これらのシミュレーションでは、上部の導電性氷の蓋の下にある、温かい対流氷で構成される弱い層と液体の水とを区別することができませんでした。多重環構造への遷移が深さで同様のレオロジー遷移を示し、このレオロジー遷移が氷と海の境界面に対応すると仮定すると、エウロパの氷の殻全体の厚さは 19 ~ 25 km になるでしょう。
カラニッシュとタイヤは、中心からほぼ 100 km まで延びるいくつかの同心円状の環状地溝を示すヴァルハラ型の多重環状盆地です。これらの多重リング盆地は、クレーターの縁内の中央盆地領域と、縁を越えた内輪領域と外輪領域の 3 つの領域で構成されています。地溝、溝状の特徴は、一対の正反対の正断層 によって生成され、外側のリング領域のリングを構成します。盆地リングは、一時的なクレーターの崩壊が、強いリソスフェアの下にある弱い物質の流れによって吸収されるときに形成されます。内向きの流れはリソスフェアを引き込み、伸長と正断層の形成を引き起こします。リソスフェアが十分に薄い場合、いくつかの同心の地溝が形成されると予想されます。したがって、多重リング盆地形成はターゲットの熱機械構造に敏感であり、エウロパ上の多重リング盆地形成のシミュレーションは、その氷殻の厚さと熱構造についての洞察を提供することができます。私たちは、iSALE-2D 衝撃物理コード ( 29 – 31 ) を使用して、エウロパ上のマルチリング盆地の形成をシミュレートしました。私たちは、メッシュ空間解像度 50 m で秒速 15 km でエウロパのような目標に衝突する半径 1.0 ~ 1.8 km の衝突体を検討しました。我々は、5~10 kmの導電性蓋に相当する34.60~17.31 K/kmのリソスフェア温度勾配で、10~50 kmの厚さの氷殻をテストしました。シミュレーションの主な制約として、観測された地溝 に基づく半径方向のひずみを使用しました。半径方向のひずみは、地溝によって受け入れられる拡張の大きさを表し、盆地の外側からその中心に向かう地溝の半径方向の変位を累積することによって計算されます。私たちのモデル設定と材料パラメーターは以前の研究 と一致しています。衛星の多環盆地形成のシミュレーションを動機として、ひずみに対する指数関数的な依存性を持つ損傷モデル と、ひずみの局在化を強化して断層のような挙動を引き起こす可能性があるダイラタンシー モデル も組み込みました。詳細については、「材料と方法」を参照してください。
結果
厚い氷殻の上に形成された多重リング盆地
私たちの基準モデルは、厚さ 6 km の導電性蓋と総厚さ 20 km の氷の殻を持つターゲットに 15 km/s で衝突する半径 1.5 km のインパクタです。6 km の導電性蓋は、熱伝導率が 3 W m^-1 K^-1 であると仮定すると、86 mW/m 2の熱流に相当することに注意してください。エウロパへの推定平均衝突速度は 26 km/s ですが、クレーターのスケーリングの法則は、26 km/s では、15 km/s で衝突する衝突体の 0.7 倍小さい衝突体が同じサイズの過渡現象を生成することを示唆しています。クレーターとなり、同様の盆地形態が形成されます。まず、クレーター崩壊のダイナミクスと、発生する総塑性ひずみに焦点を当てます。iSALE の断層は、個別の滑り面ではなく、局所的な全塑性ひずみの領域として現れます。衝撃により衝撃波が発生し、その後すぐに希薄化または解放波が発生します。これらの波の通過により物質が動き始め、深さ 19 km の一時的なクレーターが掘削されます (図 1Aおよび図 S1A)。一時的なクレーターは重力によって崩壊し、中央に大きな隆起が生じます(図1Bおよび図S1B)。中央の隆起が崩壊するにつれて、盆地中心から離れた物質は依然として内側に移動しており、盆地に向かう方向と遠ざかる方向の両方を切る小規模な正断層が形成されています(図1Cおよび図S1C)。中央隆起の崩壊により別の空洞が形成され、さらに空洞が崩壊し、より多くの内向きの流れが生じます。氷の内向きの流れの大部分は、表面から深さ約 8 km の弱い物質によって吸収され、盆地の中心から 50 km を超える深さの物質の内向きの流れのほとんどは、内向き崩壊の第 2 段階で発生します (図 1Dおよび図 1D)。図S1D)。崩壊の第 2 段階では、崩壊の第 1 段階で生じた正断層のひずみが 4 ~ 5 倍に増加します (図 1、C および D、図 S1、C、D)。2000 秒後、クレーターは最終状態に落ち着きます (図 S2A)。タイヤとカラニッシュの周囲で観察されたリングを構成する断層 (図 S3) と比較して、私たちのシミュレーションでは、より小さなオフセットを持つより多くの正規断層が生成されます (図 S4 を参照)。より低い解像度でのテストは、より高い解像度を考慮するとひずみの局在化が強化されることを示唆しています。ひずみの局在化を強化するレオロジーを考慮すると 、より大きなオフセットを持つ少数の断層にひずみが局在化する可能性が高くなります。しかし、断層の様式とこれらの断層によって適応される全ひずみは観測結果と一致しています。

図1。氷のマルチリング盆地の形成に関する基準モデルの時系列。
シミュレーションは、厚さ6kmの導電性蓋を持つ厚さ20kmの氷殻に半径1.5kmの衝突体を衝突させるものである。材料は総塑性ひずみに応じて色付けされます。白い破線の曲線は、マテリアルの境界 (つまり、氷の殻と海洋) を示します。挿入図は、導電性の氷の蓋の上部 6 km と地溝が形成される盆地の外側部分の拡大図です。図 S1 は総塑性ひずみを対数スケールで示し、図 S1 は総塑性ひずみを示します。S4 は 600 秒の地溝の位置を示しています。ムービーS1はこの図をアニメーション化したものです。( A ) は一時的なクレーターの形成を示し、 ( B ) は中央隆起の形成を示し、 ( C ) は断層の形成を示し、 ( D ) は崩壊の二次段階での断層の強化を示します (主要な部分を参照)詳細についてはテキストを参照してください)。
観測された断層オフセット からの半径方向ひずみの推定により、地溝が発生する盆地の中心から 30 ~ 100 km の領域でモデルと観測を定量的に比較することができます (図 S3)。トレーサー粒子の半径方向の変位を追跡することにより、モデルの半径方向のひずみを計算します (材料と方法)。厚さ 20 km および 30 km の氷殻のシミュレーションでは、観察された放射状ひずみがよく再現されています (図 2A )。厚さ 20 km および 30 km の氷殻の半径方向のひずみは、カラニッシュで測定された最大ひずみ 0.6 ~ 1.2% の範囲内で 40 km で 0.8% です (図 2A )。タイヤはカラニッシュよりも大きく、盆地の中心から 40 km では半径方向の最大ひずみが 1.0 ~ 1.5% 大きくなります (図 3B を参照)。盆地の中心 (または任意の場所) から 40 km の位置で観測的に導出されたひずみ推定値は、その表面が元の位置から盆地の中心に向かって内側に移動することによってその場所で経験した半径方向のひずみの総量を表すことに注意してください。このひずみを決定するには、その点の外側のすべての断層に沿ったオフセットを追加する必要があります ( 21、22 )。タイヤとカラニッシュで観察されたように、純粋な伸長テクトニクスの場合、半径方向のひずみは盆地の中心に向かって移動するにつれて単調増加します。厚さ8km、10km、および15kmの氷殻シミュレーションでは、盆地の中心に向かって移動するにつれて半径方向のひずみは単調増加しません(図2B )。半径方向のひずみの局所的な減少は、中央の隆起が崩壊して材料を外側に押すときに発生する圧縮塑性ひずみと推力断層を表しています (図 S5 および S6)。したがって、15 km より薄い氷の殻は、観察された盆地の外輪と一致しません。Melosh と McKinnon ( 24 ) は、リソスフェアの下にある弱いアセノスフェアが流動的すぎる場合、クレーター底の振動によって外向きの波が生成され、その結果、放射状および同心円状の破壊が生じると予測したことに注目します。私たちのシミュレーションは、リングテクトニクス理論を広く検証しています アセノスフェアが弱すぎる場合にはヴァルハラ型多環盆地は生成されないという結論を含む。厚さ 20 ~ 50 km の氷殻の場合、氷殻の厚さが増加するにつれて盆地中心から 40 km の半径方向のひずみが減少することを除いて、結果は同様です。この類似性は、氷の多環盆地の形成において海洋が限定的な役割を果たしていることを示唆しています。さらに、現在の観測上の制約では、厚さ 20 ~ 50 km の氷殻はカラニッシュで観測された放射状ひずみを再現することができ、これらの盆地が氷殻の厚さの下限制約を提供するだけであることを示唆しています。しかし、ヴァルハラ型のマルチリング盆地では、クレーターの崩壊時に容易に流れることができる、暖かく弱い氷の上に重なる比較的薄い導電性の氷の殻が必要です。この熱構造は、暖かい内部と地下海洋を備えた氷の天体で発生する可能性が高いため、ヴァルハラ型多重環盆地形成における海洋の役割が限られているにもかかわらず、ヴァルハラ型多重環盆地と海洋世界とのつながりが依然として期待されています。

図2。半径方向のひずみに対する氷殻の厚さの影響。
半径方向のひずみは、初期深さ 1 km で計算されます (詳細は「材料と方法」を参照)。初期深さの選択は結果にほとんど影響を与えません (図 S11A)。( A ) カラニッシュの観測結果と比較した、インパクタ半径 1.5 km のシミュレーションによる半径方向ひずみ。それぞれの太い色の線は、異なる氷殻の厚さでのシミュレーションの結果を示しています (凡例を参照)。(A) の細い灰色の線は、カラニッシュ ( 21、22 )で観測された断層オフセットから決定された、さまざまな方位角での半径方向のひずみプロファイルです。8 km の氷の殻には導電性の蓋しか含まれていないことに注意してください。他のすべてのシミュレーションには、対流する氷を覆う厚さ 6 km の導電性蓋が含まれます。( B ) の影付きの領域は、圧縮断層と推力断層の領域を表します。

図3。導電性蓋の厚さとインパクタ半径が半径方向のひずみに及ぼす影響。
図 2と同じ図ですが、厚さ 20 km の氷殻上のさまざまな導電性蓋の厚さ (蓋導電性) と衝突子の半径 ( r imp ) を示しています (凡例を参照)。( A ) は、観測的に導出されたカラニッシュの半径方向ひずみと比較した半径 1.5 km のインパクタを使用したシミュレーション結果を示し、( B ) は、観測的に導出されたタイヤの半径方向ひずみと比較した、半径 1.8 km のインパクタを使用したシミュレーション結果を示します。(A) の細い灰色の線は、カラニッシュで観察された断層オフセットから決定された異なる方位角での半径方向のひずみプロファイルであり、(B) ではタイヤについてのそれです ( 21、22 )。
インパクターのサイズと導電性蓋の厚さは半径方向のひずみに影響します
氷殻の厚さ以外に、シミュレーションを最も制御できるパラメーターは、インパクターのサイズと氷殻の熱構造です。まず、厚さ 6 km の導電性蓋を使用したシミュレーションにおけるインパクタ サイズの影響について説明します。半径 1.0 km の衝突体によって生成される半径方向のひずみは、観察された盆地リングを説明するには小さすぎるため (図 4 )、シミュレーションでは明らかな断層は発生しません (図 S7)。厚さ 10 km の氷殻上の半径 1.2 km の衝突体の最終的な半径方向のひずみには明確な圧縮ゾーンはありませんが (図 4A )、中央隆起の崩壊中に衝上断層が発生していることがわかります (図 4A)。 .S8)、これは観察と一致しません。半径 1.2 km の衝突体が厚さ 20 km または 30 km の氷の殻に衝突すると、カラニッシュに適切に適合する放射状のひずみが生じます。ただし、厚さ 20 ~ 30 km の氷殻に対する、より大きな半径 1.5 km の衝突子のシミュレーションを推奨します。これにより、半径 1.2 km の衝突子よりもわずかに大きな半径方向のひずみと盆地中心からさらに広がる非ゼロの半径方向のひずみが生成されます。シミュレーション (図 4、B および C )。増大した放射状ひずみと断層の横方向の範囲は、盆地の中心から最大 75 km まで広がるカラニッシュの観察された環とより一致しています。20 kmの氷殻上のより大きな半径1.8 kmの衝突体はより大きな半径方向のひずみをもたらしますが、シミュレーションでは観測と一致しない圧縮も示されています(図4B)。したがって、一般に、インパクターのサイズを大きくすると、結果として生じる半径方向のひずみの大きさと横方向の広がりが増加し、それに応じてリングが盆地の中心からさらに離れて形成されることがわかります。しかし、衝突体のサイズが大きすぎると、その後の大きな中央隆起の崩壊によって氷の殻が外側に押し出され、観測と矛盾する位置に圧縮特徴が生じる可能性があります(図4)。

図4。インパクターの半径と氷殻の厚さが半径方向のひずみに及ぼす影響。
図 2と同じ図ですが、10 ~ 30 km の氷殻ケースの衝突半径 ( r imp ) を示しています。( A ) は厚さ 10 km の氷殻、( B ) 厚さ 20 km の氷殻、( C ) は厚さ 30 km の氷殻のシミュレーション結果を示しています。細い灰色の線は、カラニッシュの観測された断層オフセットから決定された、異なる方位角での放射状ひずみプロファイルです ( 21、22 )。すべてのシミュレーションは、対流する氷の上に厚さ 6 km の導電性蓋があることを前提としています。
氷殻の熱構造の影響を分離するために、衝突体の半径と氷殻の厚さをそれぞれ 1.5 km と 20 km に固定したまま、導電性の蓋の厚さの影響について議論します。厚さ 5 km の導電性の蓋を考慮すると、氷の殻が弱すぎるため、中央隆起の崩壊によってリングが観察される領域に強い圧縮が生じ、これは観察と矛盾します。しかし、265 Kで対流する氷の上にある厚さ6〜7 kmの導電性の氷の蓋は、観測されたカラニッシュ井戸の放射状ひずみを再現します(図3A )。これは、より小さなクレーターの形態に基づいて、 Silber と Johnsonによって発見された好ましい熱構造と一致しています。導電性の蓋が厚すぎ(≧8 km)、氷の殻が強すぎる場合、盆地の中心から約45 kmの内側に強い圧縮領域が発生します(図3A)。タイヤまたはカラニッシュの外輪領域には明確な圧縮特徴が観察されないため、これらのモデルは好ましくありません (図 S3)。さらに、これらの厚い導電性蓋の場合、リング形成と一致する局所的な特徴は見られません(図S9)。これらのより強力な氷殻の場合、中央隆起の崩壊は、厚さ 6 km の導電性蓋の場合のように単純に伸びの大きさを減少させるのではなく、盆地の中心近く (40 km の内側) で圧縮を引き起こします。これは、より厚い導電性蓋がリング形成を引き起こさないにもかかわらず、これらのモデルが盆地の中心から 40 km の外側で同様の半径方向のひずみをどのように維持するかを説明します。したがって、我々は、局所的なリング状の特徴を生成し、より小さなヨーロッパのクレーターの形態を再現するために必要な熱構造の以前の推定と一致する、6 km の導電性蓋を好みます ( 17 )。
私たちのシミュレーションは、エウロパの氷の殻が、暖かい対流する下層の上にある導電性の蓋で構成されていることを示唆しています。シルバーとジョンソン は、海洋上の完全に導電性の氷の殻も、エウロパのクレーターの深さと直径の比率の推移を説明できると示唆しました。しかし、厚さ 8 km の純粋な導電性の氷殻 (その下に海がある) への衝撃のシミュレーションでは、10 km および 15 km の氷殻の場合と同様の圧縮ひずみと推力断層が発生します。半径方向のひずみの減少は、圧縮領域を示しています (図 2B )。したがって、私たちのシミュレーションは、カラニッシュの場合、厚さ 20 km 以上で、暖かい対流する氷の上に厚さ 6 km の導電性氷の蓋で構成される氷の殻を明らかに支持しています。対流温度の選択も、多重リング盆地の形成に別の影響を与えます。対流温度が 255 K と低いため、対流副層内の降伏強度が大きくなります (図 S10)。その結果、対流温度が低くなり、内向きの流れが減少し、半径方向の歪みが減少します(図S11C)。入力パラメータの選択における小さな不確実性によって結果が影響を受けないことを確認するために、他の多くのパラメータを調査しました。損傷した材料の摩擦係数と最大ダイラタンシー係数を除いて、変更したパラメータのほとんどは結果にわずかな影響を与えます(補足資料および図S11およびS12)。
より大きなインパクターとより厚いタイヤ用導電性リッド
推定相当直径は 38 km で、タイヤはカラニッシュ [直径33 km ] より若干大きいです。さらに、タイヤ周囲の地溝の観察から推定された半径方向のひずみは、カラニッシュの場合よりも高い半径方向のひずみを意味します。これらのより大きな半径方向のひずみは、基準シミュレーションの半径 1.5 km と比較して、半径 1.8 km のより大きな衝突子の結果であることがわかります。厚さ 6 km の導電性蓋上の半径 1.8 km のインパクターは圧縮を示しますが (図 3A)、厚さ 8 km の導電性蓋上の半径 1.8 km のインパクターは、観察されたタイヤウェルの半径方向の歪みを再現しました (図 3A )。図3B)。このシミュレーションでは、局所的なリング状構造も形成されます (図 S13)。これは、同じ厚さ 8 km の導電性蓋を備えた半径 1.5 km のインパクターの場合には見られません (図 S9)。タイヤ (厚さ 8 km の導電性蓋) とカラニッシュ (厚さ 6 km の導電性蓋) に最適な導電性蓋の厚さのわずかな違いは、エウロパの熱流の空間的または時間的変化の結果である可能性があります。厚さ 7 km の導電性蓋は両方のケースに限界適合を生成するため、タイヤとキャラニッシュの導電性蓋の厚さが同様である可能性を排除できないことに注意してください。半径 1.8 km のインパクターを使用した実験で導電性の蓋が厚くなる (9 km 以上) と、盆地の中心近くで圧縮が発生します (図 3B )。繰り返しますが、これは地溝帯に圧縮の形態学的兆候が見つからないという観察結果と矛盾しています [( 21 , 22 )、考察も参照]。これらの傾向は、半径 1.5 km の衝突体で見られる傾向と類似しています (図 3Aおよび4B )。全体として、厚さ 8 km の導電性蓋を備えた厚さ 20 km 以上の氷の殻に衝突する半径 1.8 km の衝突体が、タイヤに最適なモデルです。
議論
私たちのシミュレーションは、観測されたエウロパの多重リング盆地の構造を再現するには、暖かい対流下層を覆う導電性の蓋で構成される厚さ 20 km を超える氷の殻が必要であることを示しています。また、衝突後の構造や、将来の宇宙船ミッションで観測される可能性のある、それに関連する氷殻の海洋隆起も考慮することができます。私たちの薄い氷の殻(10 kmと15 km)の場合、氷と海の境界面に大きな隆起が見られます(図S5DとS6D)。等静性を通じて、この隆起は、観測されたよりも深い、深さ 0.5 km の盆地を生成します [<0.1 km]。この隆起は、盆地が現在の地形に一致するように粘弾性的に緩和する必要があります。対照的に、20 kmの氷殻ケースでは、氷と海の境界面の隆起はほとんどありません(図S2)。マルチリング盆地の形成に必要な氷殻の暖かく弱い部分の効率的な内向きの流れにより、衝突後にほとんど乱れのない最終的な氷殻の厚さが得られます。これにより、地形が無視できる最終的なクレーター底が形成されます。したがって、最も適切なモデルでは、観察された地形と一致するために、衝撃後の粘弾性緩和を制限する必要があります。いずれの場合も、盆地の中心には融解プールが含まれており(図S2B)、厚い氷の殻の場合でも、表面と海洋の間で交換が起こる可能性があります。
私たちの結果は、インパクターのサイズとリソスフェアの厚さの間にはある程度のトレードオフがあることを示しています。私たちは、より厚いリソスフェアを伴うより大きな衝突体と、より薄いリソスフェアへの小さな衝突が同様の結果を生み出す可能性があることを発見しました(図3)。また、衝突体が大きくなると、一般に半径方向のひずみが大きくなり、盆地の中心からさらに離れたところにリングが形成されることもわかりました。この結果は、盆地リングの範囲は一時的なクレーターのサイズに比例するが、リソスフェアの厚さに反比例するというMelosh によって提唱されたスケーリング とほぼ一致しています。しかし、衝突体が大きすぎる場合、では考慮されていなかった中央隆起の崩壊により、広い圧縮領域が生じることがわかります (図 4 )。したがって、スケーリング は注意して使用する必要があります。
我々は、伸張テクトニクス(地溝)が観察される多重環盆地の外輪領域に焦点を当てており、半径方向のひずみに対して定量的な制約を与えています。タイヤとカラニッシュの内輪領域には、環状の山塊/尾根が存在します。山塊や尾根は通常、圧縮テクトニクスを暗示していることに言及する必要があります。しかし、タイヤとカラニッシュの内側の尾根は、破壊または伸張によって形成された傾斜したブロックのように見えます。これまでの研究では、での暫定的な提案を除いて、圧縮の結果として内側の隆起が生じるという仮説を立てていません。それにもかかわらず、内部領域に明白でない、または不可解な圧縮が存在する可能性を排除することはできません。より厚い導電性蓋を使用したシミュレーションでは、盆地の中心から 30 ~ 40 km で半径方向のひずみが減少しており、これは圧縮テクトニクスを示しています (図 3A では導電性蓋の厚さが 7 ~ 10 km、導電性蓋が 8 ~ 10 km)図3Bの厚さ)。これらの同じシミュレーションには、外輪領域での観察と一致する拡張特徴と半径方向のひずみが含まれています。したがって、内側のリング領域が圧縮を示している場合、20 km より厚い氷殻を使用したシミュレーションにより、内側のリング領域の圧縮と外側のリング領域の拡張を説明できます。対照的に、薄い氷の殻では、逆の構造パターンが発生します。薄氷シェルのシミュレーションでは、盆地から 30 ~ 40 km で伸長とそれを超えると圧縮が示され (図 2B )、これは観測結果と一致しません。
エウロパの氷殻の厚さの横方向の変化は、地球規模で限定されていると考えられています。したがって、ある場所の氷の殻の厚さをヨーロッパ全体に推定するのは合理的です。ただし、エウロパの氷の殻の厚さは時間の経過とともに大幅に変化する可能性があることが示唆されています 。エウロパの平均表面年齢はわずか 20 ~ 200 Ma であると推定されています が、タイヤとカラニッシュの両方が同様の年齢である可能性は低いです。タイヤは、厚さ 8 km のわずかに厚い導電性の蓋を備えたターゲットに衝撃を与えると最適であることがわかりました。これは、エウロパの熱流の空間的または時間的変化を示している可能性があります。しかし、どちらの盆地も、形成時に約 20 km より厚い氷の殻が必要です。これは、一時的な厚さの変化によって、現代において氷殻の厚さが 20 km 以下に減少する可能性は低いことを示唆しています。厚さが 20 km を超える氷の殻は、対流する下層 ( 44 )上の導電性の蓋で構成されている必要があります。これは、対流氷層の上に導電性の氷の蓋を持つ最小シェル厚さ 20 km に関する制約と一致します。厚さ 20 km の氷殻は、クレーターが浅くなり、多重リング構造を示す直径に基づく推定値とも一致します [氷殻の厚さは 19 ~ 25 km。シェンク ]。しかし、私たちの研究は、氷のマルチリング盆地の形成が、その上に形成される氷の殻の最小厚さに制約を与えることを示唆しています。したがって、で示唆されているように、エウロパの氷の殻は 20 km より厚い可能性があり、ガニメデとカリストの氷の殻は 80 ~ 105 km よりかなり厚い可能性があります。
材料と方法
数値的手法
エウロパの多重リング盆地形成を調べるために、iSALE-2D 衝撃物理コード を使用して衝突シミュレーションを実行します。iSALE コードは、惑星の衝突とクレーターをモデル化するために開発され、さまざまな状態方程式と強度モデル を含めることによって SALE コード から改良されました。球形の氷の衝突体が、地下海の上にある氷の殻からなる平らな標的に衝突すると仮定します。氷のマテリアルには Tillotson 状態方程式 (EOS) を使用し、水の海洋には ANEOS を使用します 。衝突体のサイズは半径 1.0 ~ 1.8 km の範囲にあり、これは木星系彗星のサイズの上限に相当します。ターゲットとインパクターに同じ EOS を使用するため、それらの密度は温度と圧力に依存します。それらの参照密度は 910 kg/m^3 です。我々は、Bray の強度モデル パラメーター を使用します。これは、無傷の氷 と損傷した氷の実験室測定に適合します。適度に斜めの衝撃の影響を近似するために、軸対称シミュレーションの衝撃速度は、斜めの衝撃の垂直成分であるとみなされることがよくあります。私たちが選択した 15 km/s は、約 35°の衝突角度での 26 km/s の斜め衝突速度の垂直成分に相当します。15 km/s での垂直衝撃のシミュレーションも計算コストを削減し、以前の研究との一貫性を維持します。我々は異なる衝突体のサイズを調査するだけですが、衝突速度の変動も結果に同様の影響を与えるでしょう。マルチリング盆地内の地溝を解決するには、50 m の解像度を使用します [iSALE の高解像度ゾーンのドメイン サイズは、水平 (半径) 方向に 100 km、垂直方向に 5 km です]。計算メッシュ領域は、結果に影響を与える可能性のある反射を防ぐのに十分な大きさであることに注意してください (iSALE の拡張ゾーンは、水平方向で最大 ~800 km、垂直方向で約 -400 ~ ~140 km をカバーします)。
エウロパの氷殻の厚さを自由パラメータとして扱い、厚さ 8、10、15、20、30、40、50 km の氷殻への衝突をシミュレートします。ターゲットの表面温度は 100 K であると仮定します。ターゲット内の温度プロファイルは、盆地形成の主な制御の 1つです。基準ケースとして、温度 265 K の対流下層上の厚さ 6 km の導電性氷の蓋で構成される氷殻を検討します。導電性氷蓋内の温度勾配は 28.85 K/km です。これは、エウロパの小さなクレーターの深さと直径の比を説明できる氷殻構造の 1 つです。温度プロファイルの影響をテストするために、厚さ 6 km の導電性蓋を備えた基準ケースから導電性蓋の厚さを 5 ~ 10 km の範囲で変化させました。また、対流温度が 255 K、導電性の蓋の厚さが 6 km のターゲットも検討します。これも、より小さなクレーターの形態を再現することがわかっています 。また、厚さ 8 km の完全に導電性の氷殻への衝突もシミュレーションしました。これにより、ヨーロッパのより小さなクレーターの形態も説明できます 。以前の研究に基づいて、シミュレーションに粘弾塑性氷レオロジーを含め、に続くダイラタンシー モデルを含めます。材料の入力パラメータを表 S1 にまとめます。
観測との一致を評価するために、トレーサ粒子の半径方向の変位を使用して半径方向のひずみを計算します。iSALE シミュレーションのラグランジュ トレーサ 粒子は、クレーター形成中のオイラー グリッドを通る物質の塊の動きを追跡します。表面近くの層の細胞は噴出物の定置によって過度に影響を受ける可能性があるため、最初の深さ約 1 km での半径方向の変位を考慮します。初期深さ (0.5 ~ 1.5 km) の半径方向ひずみへの依存性を調査したところ、シェル内の初期深さの選択は、盆地から 40 km を超える距離での基準ケースの半径方向ひずみプロファイルに影響を及ぼさないことが確認されました。中央(図S11A)。一方、より深い深さ (3.0 km および 4.0 km) での半径方向のひずみを考慮すると、半径方向のひずみは小さくなり、表面で観察される変形を表すものではなくなります。地溝は、タイヤとカラニッシュの盆地中心から水平距離約 40 ~ 80 km の範囲で観察されます (図 S3) 。盆地全体が中程度の解像度で画像化されているため、盆地中心の定義がタイヤにとってより適切であることに注意してください。カラニッシュ盆地の約半分だけが中程度から高解像度で画像化されており、これにより中心のフィットと半径方向のひずみのオフセットに不確実性が生じる可能性があります。Singerらの研究に続いて、は観測の半径方向のひずみを表し、100 km から中心に向かって半径方向の変位を ΣΔ r /( r + ΣΔ r ) として累積します。ここで、 rは半径方向の距離、Δ rは半径方向の距離です。変位; したがって、ΣΔ r は合計の内側への変位を表し、分母 ( r + ΣΔ r ) は初期距離を示します。数値シミュレーションでは、半径方向のひずみを計算するために、指定された初期深さにあるすべてのトレーサー粒子を考慮します。衝撃波の通過は衝突後 50 秒で終了するため、これをその時点のトレーサー粒子の半径方向の距離 [すなわちr ( t = 50)] と見なします。合計の内側への変位は、ΣΔ r = r ( t = 50) − r ( t= 2000)、正の値は内側への変位を示します。トレーサ粒子が受ける総塑性ひずみに関係なく、トレーサ粒子の内側への変位を計算することに注意してください。計算された半径方向ひずみの滑らかな変化は、シミュレーションにおける半径方向ひずみが現実ほど局所的ではないことを示すもう 1 つの指標です。観察された放射状ひずみの変動は、自然変動、またはカラニッシュの場合には利用可能なガリレオ画像を使用して盆地の中心を決定する際の不正確さに起因する可能性があります。したがって、観測によって得られたひずみデータと数値シミュレーションを水平方向に比較します。観察された地溝の幅は 0.4 ~ 4.7 km、深さは 14 ~ 210 m であることに注意してください。これらの深さを解決するには、少なくとも 20 m の解像度が必要です。50 m という分解能は観測された深さを分解するには十分ではありませんが、観測された半径方向のひずみを再現するには十分であることが結果からわかります。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます