火星が軽く形成された原因が他に見つかりグランドタックシナリオは閉店のようです。木星が太陽に向かって移動しない理由が分かればグランドタックシナリオも迷わず成仏できるのです。以下、機械翻訳。
太陽系は低粘性円盤で形成された可能性がある:巨大惑星の移動からニースモデルまでの動的研究
要約
背景。低粘性原始惑星円盤 (PPD) の文脈では、太陽系の形成シナリオを再検討する必要があります。
特に、木星と土星のペアは、一般的に内側に移動しながら 2:1 の平均運動共鳴に固定されることが示されており、グランド タック シナリオは不可能です。
目的。低粘性円盤で複数の巨大惑星の共鳴チェーンがどのようなものになるか、また、これらの構成がガス円盤後の段階で太陽系を形成するように進化できるかどうかを調べます。
方法。FARGOCA コードによる流体力学シミュレーションを使用して、粘性パラメータ α = 10^−4 の円盤での巨大惑星の移動を調べました。ガスのない構成への移行段階の後、リバウンドを使用した N 体シミュレーションを実行して、得られた共鳴鎖の安定性を、残った微惑星の円盤との相互作用を通じて研究しました。
結果。巨大惑星によって開かれた隙間は、粘性が低いほど広く深くなり、円盤の減衰効果が減少します。したがって、惑星が共鳴状態に入ると、共鳴角は循環に近いままになり、鎖は弱くなります。多数の構成を調査し、4 つまたは 5 つの惑星からなる 5 つの安定した共鳴鎖を発見しました。薄い (冷たい) PPD では、4 つの巨大惑星は移動を元に戻し、外側に移動します。円盤の分散後、微惑星のベルトの影響を受けて、一部の共鳴鎖は不安定な段階を経ますが、他の共鳴鎖は 10 億年かけてスムーズに移動していきます。3 つの共鳴鎖では、最終的な構成の約 1% が太陽系に適合する 4 つの基準を満たしています。最も成功した実行は、巨大な微惑星円盤を持つ冷たい PPD で形成されたシステムで得られます。
結論。この研究は、原始惑星円盤段階から巨大惑星の不安定性に至るまで、太陽系の巨大惑星の動的歴史の完全に一貫した研究を提供します。低粘性の円盤で共鳴構成を構築することは困難ですが、冷たく低粘性の原始惑星円盤から太陽系を再現することは可能であることがわかりました。
キーワード。惑星-円盤相互作用、原始惑星円盤、惑星と衛星: 形成と動的進化と安定性
1. はじめに
私たちの太陽系は、この分野で明らかに最も研究されている惑星系です。そのため、惑星と惑星系の形成の理論をテストするための優れた実験室になりますが、その非常によく制約された特徴により、私たちのモデルを適合させることは困難です。多種多様な太陽系外惑星系の発見以来、私たちは今や私たちの太陽系を珍しいものとみなすことができます。したがって、一般的な惑星形成理論では、太陽系は起こり得る結果ではあるが、最も可能性の高い結果ではないとしている。
太陽系の寿命のさまざまな期間に焦点を当てたさまざまなモデルが、今日観測されている多数の特徴を説明するために提案されている。一方では、原始惑星系円盤 (PPD) 段階におけるグランド タック シナリオ (Walsh ら、2011) では、木星と土星の移動を利用して、地球に対する火星の質量の低さと小惑星帯の構成の変化を説明できる可能性がある。このモデルでは、木星は 1.5 au 程度に達するまで内側に移動し、その時点で土星は 3:2 の平均運動共鳴 (MMR) に固定され、木星は Masset & Snellgrove (2001) のメカニズムにより移動方向の反転を引き起こす。しかし、火星の質量の低さと小惑星帯の減少を説明する別のメカニズムが発見されたため、グランド タック モデルは魅力を失いつつあります (例: Dr˛a˙zkowska
et al. 2016; Clement et al. 2018, 2019; Nesvorný et al. 2021;Morbidelli et al. 2022)。
しかし、木星の内側への移動を阻止することは、木星が他の恒星の周りで観測されるほとんどの木星質量惑星に典型的な 1-2 au の半長軸を獲得しなかった理由を説明するために依然として必要です。一方、原始惑星系円盤が消散すると、巨大惑星はコンパクトな共鳴構成になりますが、今日の太陽系は非常に異なる状況にあります。したがって、太陽系の形成の最終段階を説明するには、別のモデル、つまりニース モデルが必要です。これは、激しい不安定性によって惑星が現在の位置に至った経緯を説明する魅力的なシナリオです。この不安定性は、巨大惑星と太陽系の端にある残存微惑星の円盤との間の重力相互作用によって引き起こされました。このモデルは、巨大惑星と木星のトロヤ小惑星の軌道構成、または小惑星帯と残存カイパーベルト内の小惑星の大きな離心率と傾斜角から始めて、現在の太陽系におけるさまざまな制約を同時に再現することができます (レビューについては、Nesvorný 2018 を参照してください)。
初期の惑星配置の選択と不安定性の特性は、ニース モデルのさまざまな研究を通じて進化してきました。オリジナルのニース モデル (以下 ONM、Tsiganis 他 2005、Morbidelli 他 2005、Gomes 他 2005) では、この不安定性の引き金となる、木星と土星の間の 2:1 MMR の内側から外側への交差に焦点が当てられました。惑星が微惑星と角運動量を交換すると、土星、天王星、海王星の場合は外向きに、木星の場合は内向きに移動し、微惑星は太陽系から追い出されます。微惑星が発散移動をすると、木星と土星は 2:1 MMR に近づき、これがそれらの離心率を刺激し、最終的にシステムが不安定になります。残った微惑星は、惑星の軌道を今日知られている安定した構成に戻すのに役立ちます。ONM は、木星と土星の離心率がゼロでない理由を説明します。また、不規則衛星の分布、木星のトロヤ群、メインベルト内の小惑星の分布、そして最終的には後期重爆撃 (LHB) のシナリオとも一致しています。最初のニース モデル研究当時の LHB は、太陽系の歴史の後半 (約 7 億年頃) に巨大不安定性が発生する主な制約の 1 つでした。ただし、ONM では、不安定性のタイミングは微惑星の円盤の初期位置に大きく依存していました。ONM のもう 1 つの弱点は、惑星の初期構成が任意であることに関係しています。ガス円盤段階での惑星の移動の結果、円盤が分散するまでに惑星は共鳴構成になった可能性が高く、これは ONM では考慮されていませんでした。当時の移動研究では、木星と土星はおそらく 3:2 の MMR で固定されていることが判明しました (Masset & Snellgrove 2001; Morbidelli & Crida 2007)。そのため、Morbidelli ら (2007) は、木星と土星の研究を拡張し、天王星と海王星を追加しました。彼らは 6 つの共鳴チェーンの可能性を発見しました。そのうち 2 つは 1 億年以上安定していましたが、後に微惑星の円盤によって不安定化する可能性があります。これにより、後に Nice Model 2 と呼ばれる Nice Model が更新されました (Levison ら 2011)。このモデルでは、惑星の初期構成は、円盤段階での惑星移動を考慮した流体力学シミュレーションから取得されました。この新しいバージョンのモデルでは、著者らは、初期条件の広い範囲で不安定性が遅く発生する可能性があることを発見しました。ただし、初期には微惑星円盤が海王星から十分離れており、惑星と微惑星の散乱が起こらないことが条件です。
しかし、それ以来、月への衝突の年代順は修正されています。月への衝突が3.9 Gyr前(つまり、月の形成から6億年後)に激しかったことは事実です。しかし、アポロ計画の余波では、このような激しい衝突は、静止期の後に衝突率が急激に上昇した結果であると考えられていましたが (Tera et al. 1974; Ryder 2000)、月のサンプルの個々の鉱物と月の隕石の衝突年代の新しい分析では、その時期以前には衝突が明らかに少なかったわけではないことが示されています (Zellner 2017 を参照)。月の衝突率の単調な減少は、力学シミュレーション、月のクレーター記録、および月の後期ベニアと一致することが示されています。ただし、月が4.35 Gyr 以前にクレーターと高度に親鉄性の元素の痕跡を失った場合、つまり月のマントルがその時まで部分的に溶融していた場合、そのようになるはずです (Morbidelli 他 2018、Zhu 他 2019、Nesvorný 他 2023)。したがって、3.9 Gyr 前の月の衝突率を説明するために、後期巨大惑星の不安定性を持ち出す必要はありません。ニース モデルの不安定性に関する最も広範な研究は、Nesvorný & Morbidelli (2012) によるものです。その研究で、著者らは、惑星の初期位置、微惑星円盤の位置と質量、および系に最初に存在した惑星の数を含む幅広いパラメータ空間で、惑星の不安定性の統計的研究を行った。今日の木星の軌道励起と、その不規則衛星とトロヤ群小惑星の存在は、この巨大ガス惑星が他の惑星との遭遇を経験したに違いないという証拠を示している。その結果、その惑星は系から簡単に放出される。したがって、系の初期に4つの惑星しか存在していなかった場合、今日の太陽系を再現することはできない。したがって、Nesvorný & Morbidelli (2012) は、最終的に木星によって放出される3番目、さらには4番目の巨大氷惑星が存在する可能性を検討した。ただし、彼らの研究では、惑星の初期位置は、ガス円盤フェーズを模倣した移動処方を使用して設定されている。これにより、共鳴鎖構築のより安価でより広範な調査が可能になりますが、流体力学的シミュレーションのように惑星とディスクの相互作用の複雑さをすべて再現するわけではありません。
ディスクフェーズの終わりにおける巨大惑星の正確な初期構成はわかりませんが、ニースモデルの出発点として、現実的な移動履歴を考慮することが重要です。原始惑星系円盤の物理は、共鳴惑星系の構築にかなりの影響を及ぼします。これまでに引用したすべての研究の時点では、原始惑星系円盤は非常に粘性が高いと考えられていました。しかし、現在では円盤はそれほど乱流ではないと考えられています(理論的議論のレビューについては、Turner et al. (2014) または Lesur et al. (2022) を、観測的制約については Pinte et al. (2016)、Dullemond et al. (2018)、Sellek et al. (2020)、Villenave et al. (2022) を参照してください)。Pierens et al. (2014) の結果に加えて、私たちは最近 Griveaud et al. で次のことを示しました。 (2023) は、低粘性円盤における惑星ペアの移動は、高粘性の場合とは大きく異なることを明らかにしました。木星と土星は、3:2 ではなく 2:1 MMR で固定されています。ただし、Pierens ら (2014) とは異なり、私たちの研究では、この構成でペアの外向きの移動は確認されていません。この結果は、円盤の質量、アスペクト比、および外惑星の初期位置と質量の変更に関して堅牢であることを示しました。前回の論文で述べたように、2 つの研究はエネルギー方程式の扱いと表面密度プロファイルが異なります。これらの違いが、ペアの移動方向の違いを説明できる可能性があります。それでも、前回の研究から、上記のグランド タック シナリオは、太陽系の原始惑星円盤の粘性が低い場合は不可能であると結論付けることができます。しかし、前述のように、グランド タックはもはや必要ないため、低粘性の原始太陽系星雲が考慮される可能性が開かれますが、木星の内側への移動を阻止するメカニズムを見つけることが重要です。したがって、この論文では、Griveaud ら (2023) の結果をニース モデルに拡張することに興味があります。
参考までに、ニース モデルに関するこれまでに引用された研究のほとんどは、木星と土星を 3:2 構成としていました。
一部の研究では、主に学術目的で、木星と土星を 2:1 MMR とする共鳴チェーンをいくつか散発的に検討しました (Nesvorný & Morbidelli 2012、Batygin & Brown 2010、Thommes ら 2008、Pierens ら 2014)。最近では、Clement らが、木星と土星を 2:1 MMR とする共鳴チェーンをいくつか散発的に検討しました。 (2021b,a) は、2 つの惑星の離心率を 0.025 から 0.25 の範囲で調整する 2:1 共鳴における木星と土星の不安定性を広範に研究しました。
しかし、これらの研究はすべて、原始惑星系円盤の物理的性質に関係なく共鳴チェーンを構築し、簡略化された方法で惑星の移動を模倣しました。対照的に、Crida (2009) は、流体力学的シミュレーションを使用して、さまざまな密度プロファイルの粘性円盤内の 4 つの太陽系巨大惑星の移動を研究しましたが、円盤後の段階については取り上げませんでした。私たちの知る限り、Morbidelli ら (2007) だけが、単一の研究で両方の段階を統合し、惑星の移動と巨大惑星の不安定性の間に橋を架けました。彼らの研究と同様に、本論文の目的は、低粘性円盤の文脈で、太陽系の巨大惑星の軌道進化を原始惑星円盤段階から今日の構成まで自己矛盾なく研究することです。まず、そのような円盤で共鳴構成がどのように形成されるか、低粘性がどのようにこれらのシステムの構築に影響を与えるかを調べます。次に、流体力学シミュレーションの出力をニースモデルのN体シミュレーションの初期条件として使用します。
また、Morbidelli ら (2007) は地球全体の不安定性の概念実証 N 体シミュレーションをいくつか示しただけでしたが、私たちは太陽系の再現の成功率を評価します。
この論文は 2 つの主要なセクションに分かれています。セクション 2 では、原始惑星系円盤内の惑星移動の段階について説明します。
まず、セクション 2.1 で流体力学シミュレーションの実行方法について説明します。次に、セクション 2.2 で、2 つの異なる円盤スケールの高さでの 4 つまたは 5 つの惑星の移動の結果を示します。N 体シミュレーションに移行するために、セクション 2.4 でガス円盤の散逸を模倣し、惑星系への影響について説明します。セクション 2.5 では、低粘性円盤での共鳴チェーンの形成に関する「中間的な」結論を示します。論文はセクション 3 に続き、以前に構築された共鳴チェーンからガス ディスクが分散した後の巨大惑星の不安定性段階を研究します。セクション 3.1 で手法を示し、セクション 3.2 で Nesvorný & Morbidelli (2012) の基準に基づいてシミュレーションの成功を評価する方法を説明します。結果はセクション 3.3 で示します。最後に、セクション 4 で完全な研究について説明し、結論を出します。

図 1. 公称シミュレーション N4 におけるディスクの平坦化された表面密度の時間スナップショット。空の円は、木星 (赤)、土星 (青)、天王星 (緑)、海王星 (白) の位置を示します。パネル a は、天王星が土星との 2:1 MMR に入ったことを示しています。パネル b は、海王星が天王星との 3:2 共鳴に固定された瞬間を示しています。パネル c では、4 つの惑星が最終的な共鳴構成 (2:1、3:2、4:3) に入ります。最後に、パネル d は、模擬ディスク分散フェーズの開始時の安定したシステムを示しています (詳細については、セクション 2.4 を参照してください)。これらの瞬間は、図 2 に示されている惑星軌道の進化のスナップショットです。

図 2. 公称シミュレーション N4 における 4 つの惑星の軌道パラメータの進化。網掛け部分は、惑星の近点遠心の位置、それぞれ q = a(1−e) と Q = a(1+e) を示しています。
プロットの始まりの約 150,000 年までは、Griveaud ら (2023) の公称シミュレーション N を示しています。天王星と海王星は、シミュレーションで連続して追加され、最終的な共鳴チェーンは (2:1、3:2、4:3) です。ここで、海王星の導入時間は TN,0 = 250,000 年でした (図 3 を参照)。破線と点線の垂直線は、それぞれ模擬ディスク分散の開始 (t0) と終了 (tf) の時間を示しています。詳細については、セクション 2.4 を参照してください。

図 3。図 2 と同じですが、海王星の導入時間 TN,0 = 238,000 年、つまりシミュレーション Nbis4 です。ここで、天王星は 355,000 年でシステムから排除されます。シミュレーションの後半で、天王星質量の別の氷巨星を追加し、最終的な共鳴チェーン (2:1、2:1、4:3) を取得します。

図 4。図 3 と同じですが、シミュレーション Nbis5 では、天王星質量の氷巨星がシミュレーションに追加され、最終的な共鳴チェーン (2:1、2:1、4:3、5:4) が得られました。このシミュレーションは、ガス ディスク フェーズでは安定していますが、模擬蒸発フェーズでは不安定になります (詳細についてはセクション 2.4 を参照)。

図 5。図 2 と同様に、この図は、より低温のディスク、つまりより低いアスペクト比で進化する 4 つの巨大惑星の軌道パラメータを示しています。シミュレーション C4.2 さらに、図の背景には、シミュレーション全体の時間の関数として、ディスクの方位角平均表面密度プロファイルが表示されています。わかりやすくするために、プロットの左半分には、すべての惑星の軌道パラメータが白で表示されています。プロットの後半では、約 35 万年前から、ガス ディスクの分散フェーズが開始されます。垂直の破線と点線は、このフェーズの開始 t0 と終了 tf を示しています (詳細については、セクション 2.4 を参照してください)。システムは共鳴チェーン (2:1、3:2、5:4) で安定しています。

図 6。図 5 と似ていますが、シミュレーション C5 では、質量 6M⊕ の惑星が追加されています。最終的な共鳴チェーンは (2:1、3:2、5:4、4:3) です。

図 7. シミュレーション C4 における表面密度の半径プロファイルを木星の位置に合わせて再スケールしたもの。青緑色の線は、木星と土星だけが円盤内にあるとき (基本的には Griveaud ら (2023) のシミュレーション) に対応しています。その時点 (t=142 kyr) では、図 5 に示すように、2 つの惑星はゆっくりと内側に移動しています。マゼンタ色の線は、t=308 kyr で 4 つの巨大惑星が外側に移動しているときのプロファイルを示しています。惑星の位置は円マーカーで示されています。垂直の点線は、木星の内側リンドブラッド共鳴 (ILR) と土星の外側リンドブラッド共鳴 (OLR) の位置を示しています (詳細については本文を参照)。

図 8. 外向き移動の場合のガス除去が惑星軌道に与える影響。上図: シミュレーション C4 延長 (実線)、模擬ガス蒸発段階を含む C4 (破線、図 5 に対応)、および C5 (点線、模擬蒸発段階前の図 6 に対応) による木星、土星、天王星、海王星の軌道長半径の進化。下図: 上図で説明した 2 つの C4 ケースにおける木星と土星の離心率の進化。
4. 考察と結論
この研究の目的は、太陽系の巨大惑星の原始惑星円盤段階からニースモデルまでの力学史をたどることです。私たちは、まず完全な流体力学的シミュレーションを使用して共鳴チェーンを構築し、次に模擬円盤蒸発段階の後に、最後の惑星軌道の外側に配置された微惑星円盤と惑星の相互作用を統合することでこれを達成しました。このような完全に一貫した研究は、いわゆるニースモデル2におけるMorbidelliら(2007)とLevisonら(2011)の統合研究以来行われていませんでした。しかし、これらは一方では高粘性の原始惑星円盤という状況で、他方ではニースモデルの後期不安定性の要件で行われました。それ以来、原始惑星系円盤のパラダイムは低粘性円盤へと移行し、不安定性のタイミングに関する制約はなくなりました。そのため、この新しい状況で太陽系の形成の可能性について完全に一貫した研究を行う必要がありました。まず、粘性パラメータ α = 10−4 で 2 次元流体力学シミュレーションを実行し、巨大惑星の収束移動を研究しました。Griveaud ら (2023) で、木星と土星のペアがこのような低粘性円盤で 2:1 MMR を超えることは決してないことをすでに示していました。この系に 2 つの氷巨星を追加し、2 つの異なる円盤スケールの高さに対して 3 つの異なる共鳴チェーンを発見しました。逆境にもかかわらず、5 つの惑星を持つ 2 つの共鳴チェーンも取得しました。最後に、ニース モデル フェーズを研究するために、原始惑星系円盤の蒸発フェーズを模倣し、惑星系がその構成を断熱的に再調整できるようにしました。
この研究の前半は、共鳴チェーンを構築するための流体力学的研究の重要性を示しています。上記の研究を除き、他のすべてのニース モデル研究では、惑星の離心率と半長軸に対する移動の処方または単純な減衰力のいずれかを使用して N 体積分器を使用して構築された共鳴チェーンが使用されています。この研究では、流体力学的シミュレーションで共鳴チェーンを構築することははるかに複雑になる可能性があることを示しています。チェーンの安定性は、惑星の周りのガスの分布に大きく依存します。このような低粘性の円盤では、巨大惑星が広く深いギャップを作成し、共鳴に対するガスの散逸力を大幅に削減します。したがって、低粘性円盤内の複数の巨大惑星のシステムは、特に 3 つ以上の惑星の場合は不安定になりやすい。
私たちが得た 5 つの共鳴チェーンは、ニース モデル研究で以前に研究されたものよりも幅が広い。これは、木星と土星のペアが常に 2:1 MMR にあるためである。2 つのケースでは、2 番目のペアも 2:1 MMR にあり、他のチェーンでは 3:2 にある。以前の研究では、主に学術的な目的で木星と土星を 2:1 MMR で検討していたが、2 番目のペアも 2:1 MMR で検討し、これらのシステムは非常に安定していると結論付けた研究もある (Nesvorný & Morbidelli 2012)。私たちの結果はこの声明と一致しており、シミュレーション Nbis4 と Nbis5 ではほとんど不安定性は見られない。 2 番目の惑星ペアが 3:2 MMR にある場合、文献ではこれらのチェーンが一般に不安定性を引き起こさないことも示されています (Deienno 他 2017; Clement 他 2021b; Nesvorný & Morbidelli 2012)。私たちの結果では、チェーンが冷たい PPD 内に構築されている場合、システムは微惑星ディスクと相互作用するときに非常に不安定になります。30M⊕ ディスクではシステム内のすべての惑星を維持するのに十分ではありませんが、50M⊕ ディスクでは 4 つまたは 5 つの惑星の場合でも成功した結果が得られます。ただし、チェーンが公称 PPD 内に形成される場合、システムはより安定しますが、50M⊕ 微惑星ディスクの場合は多少の不安定性が発生する可能性があります。冷たい原始惑星系円盤で形成される共鳴鎖は、惑星の近傍にガスの減衰効果がないため弱く安定していると考えられ、したがって私たちの結果と、おそらく文献との相違を説明できる。低粘性の状況では、私たちの冷たい円盤と同様にアスペクト比の低い原始惑星系円盤を考慮することが現実的である。また、そのような円盤では、4つの巨大惑星が原始惑星系円盤の段階で外側に移動し、ホットジュピターになることを防いでいることも指摘する。私たちが研究したすべてのシステムの中で、3つの構成が太陽系の制約に適合するために必要な4つの基準をそれぞれ約1%の成功率で満たしており、これはNesvorný & Morbidelli (2012) の最良のケースよりわずかに低いが、同じ桁である。図13では、原始惑星系円盤から現在までのそのような進化の例を示しています。太陽系は一般的な惑星系ではないため、統計的な成功ではなく、シミュレーションから得られる可能性のある結果だけが必要です。したがって、成功率が1%の場合、この研究は太陽系が低粘性の原始惑星系円盤から出現した。現在までに、太陽系の4つの巨星に匹敵する惑星系は発見されていないため、この構成がシミュレーションで最も頻繁に発生する結果である必要はない。結果が微惑星円盤の特性にどのように依存するか(不安定性のタイミングなど)は、この論文の範囲をはるかに超えており、今後の研究の対象となる。

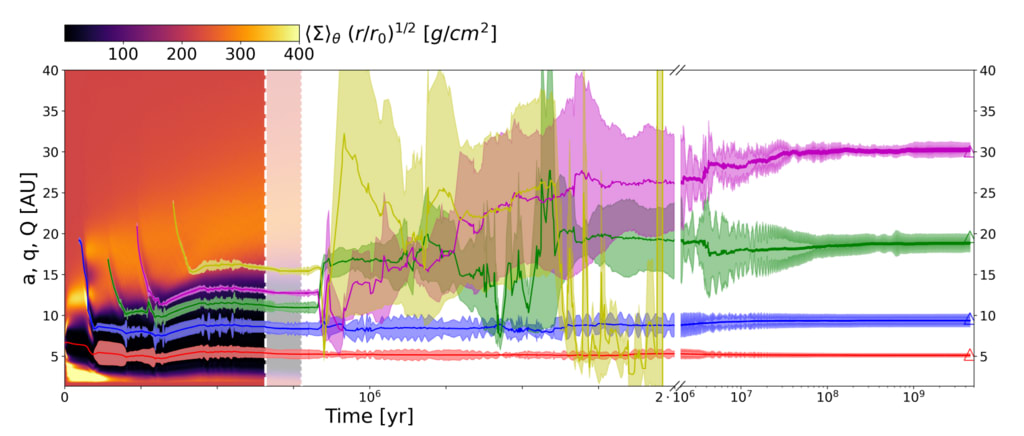
図 13. 太陽系の 4 つの巨大惑星が、低温で粘性の低い原始惑星円盤で形成され、最後の惑星から 0.5 au 離れた 50M⊕ の微惑星円盤と相互作用した場合の、その力学史の考えられるシナリオ。このシナリオでは、初期の惑星系は 5 つの惑星で構成され、5 番目の惑星は P9 に相当する可能性のある 6M⊕ の惑星です。最初の 800 kyr は、惑星が共鳴構成に移行する原始惑星円盤段階の流体力学的シミュレーションを示しています。背景には、円盤内のガス表面密度の半径プロファイルを示しています。次に、模擬ガス分散期間 (2 つの白い破線の間) をシミュレーションします。最後に、惑星が微惑星円盤と相互作用する 1 つの N 体シミュレーションの結果を示します。システムは急速に不安定になり、2 Myr 未満で 5 番目の惑星を放出します。次に、このシステムを数十億年にわたって積分し(x 軸のスケールを線形から対数に変更)、現在の太陽系の良好な類似体を取得します(三角形は巨大惑星の実際の長半径を示します)。
太陽系は低粘性円盤で形成された可能性がある:巨大惑星の移動からニースモデルまでの動的研究
要約
背景。低粘性原始惑星円盤 (PPD) の文脈では、太陽系の形成シナリオを再検討する必要があります。
特に、木星と土星のペアは、一般的に内側に移動しながら 2:1 の平均運動共鳴に固定されることが示されており、グランド タック シナリオは不可能です。
目的。低粘性円盤で複数の巨大惑星の共鳴チェーンがどのようなものになるか、また、これらの構成がガス円盤後の段階で太陽系を形成するように進化できるかどうかを調べます。
方法。FARGOCA コードによる流体力学シミュレーションを使用して、粘性パラメータ α = 10^−4 の円盤での巨大惑星の移動を調べました。ガスのない構成への移行段階の後、リバウンドを使用した N 体シミュレーションを実行して、得られた共鳴鎖の安定性を、残った微惑星の円盤との相互作用を通じて研究しました。
結果。巨大惑星によって開かれた隙間は、粘性が低いほど広く深くなり、円盤の減衰効果が減少します。したがって、惑星が共鳴状態に入ると、共鳴角は循環に近いままになり、鎖は弱くなります。多数の構成を調査し、4 つまたは 5 つの惑星からなる 5 つの安定した共鳴鎖を発見しました。薄い (冷たい) PPD では、4 つの巨大惑星は移動を元に戻し、外側に移動します。円盤の分散後、微惑星のベルトの影響を受けて、一部の共鳴鎖は不安定な段階を経ますが、他の共鳴鎖は 10 億年かけてスムーズに移動していきます。3 つの共鳴鎖では、最終的な構成の約 1% が太陽系に適合する 4 つの基準を満たしています。最も成功した実行は、巨大な微惑星円盤を持つ冷たい PPD で形成されたシステムで得られます。
結論。この研究は、原始惑星円盤段階から巨大惑星の不安定性に至るまで、太陽系の巨大惑星の動的歴史の完全に一貫した研究を提供します。低粘性の円盤で共鳴構成を構築することは困難ですが、冷たく低粘性の原始惑星円盤から太陽系を再現することは可能であることがわかりました。
キーワード。惑星-円盤相互作用、原始惑星円盤、惑星と衛星: 形成と動的進化と安定性
1. はじめに
私たちの太陽系は、この分野で明らかに最も研究されている惑星系です。そのため、惑星と惑星系の形成の理論をテストするための優れた実験室になりますが、その非常によく制約された特徴により、私たちのモデルを適合させることは困難です。多種多様な太陽系外惑星系の発見以来、私たちは今や私たちの太陽系を珍しいものとみなすことができます。したがって、一般的な惑星形成理論では、太陽系は起こり得る結果ではあるが、最も可能性の高い結果ではないとしている。
太陽系の寿命のさまざまな期間に焦点を当てたさまざまなモデルが、今日観測されている多数の特徴を説明するために提案されている。一方では、原始惑星系円盤 (PPD) 段階におけるグランド タック シナリオ (Walsh ら、2011) では、木星と土星の移動を利用して、地球に対する火星の質量の低さと小惑星帯の構成の変化を説明できる可能性がある。このモデルでは、木星は 1.5 au 程度に達するまで内側に移動し、その時点で土星は 3:2 の平均運動共鳴 (MMR) に固定され、木星は Masset & Snellgrove (2001) のメカニズムにより移動方向の反転を引き起こす。しかし、火星の質量の低さと小惑星帯の減少を説明する別のメカニズムが発見されたため、グランド タック モデルは魅力を失いつつあります (例: Dr˛a˙zkowska
et al. 2016; Clement et al. 2018, 2019; Nesvorný et al. 2021;Morbidelli et al. 2022)。
しかし、木星の内側への移動を阻止することは、木星が他の恒星の周りで観測されるほとんどの木星質量惑星に典型的な 1-2 au の半長軸を獲得しなかった理由を説明するために依然として必要です。一方、原始惑星系円盤が消散すると、巨大惑星はコンパクトな共鳴構成になりますが、今日の太陽系は非常に異なる状況にあります。したがって、太陽系の形成の最終段階を説明するには、別のモデル、つまりニース モデルが必要です。これは、激しい不安定性によって惑星が現在の位置に至った経緯を説明する魅力的なシナリオです。この不安定性は、巨大惑星と太陽系の端にある残存微惑星の円盤との間の重力相互作用によって引き起こされました。このモデルは、巨大惑星と木星のトロヤ小惑星の軌道構成、または小惑星帯と残存カイパーベルト内の小惑星の大きな離心率と傾斜角から始めて、現在の太陽系におけるさまざまな制約を同時に再現することができます (レビューについては、Nesvorný 2018 を参照してください)。
初期の惑星配置の選択と不安定性の特性は、ニース モデルのさまざまな研究を通じて進化してきました。オリジナルのニース モデル (以下 ONM、Tsiganis 他 2005、Morbidelli 他 2005、Gomes 他 2005) では、この不安定性の引き金となる、木星と土星の間の 2:1 MMR の内側から外側への交差に焦点が当てられました。惑星が微惑星と角運動量を交換すると、土星、天王星、海王星の場合は外向きに、木星の場合は内向きに移動し、微惑星は太陽系から追い出されます。微惑星が発散移動をすると、木星と土星は 2:1 MMR に近づき、これがそれらの離心率を刺激し、最終的にシステムが不安定になります。残った微惑星は、惑星の軌道を今日知られている安定した構成に戻すのに役立ちます。ONM は、木星と土星の離心率がゼロでない理由を説明します。また、不規則衛星の分布、木星のトロヤ群、メインベルト内の小惑星の分布、そして最終的には後期重爆撃 (LHB) のシナリオとも一致しています。最初のニース モデル研究当時の LHB は、太陽系の歴史の後半 (約 7 億年頃) に巨大不安定性が発生する主な制約の 1 つでした。ただし、ONM では、不安定性のタイミングは微惑星の円盤の初期位置に大きく依存していました。ONM のもう 1 つの弱点は、惑星の初期構成が任意であることに関係しています。ガス円盤段階での惑星の移動の結果、円盤が分散するまでに惑星は共鳴構成になった可能性が高く、これは ONM では考慮されていませんでした。当時の移動研究では、木星と土星はおそらく 3:2 の MMR で固定されていることが判明しました (Masset & Snellgrove 2001; Morbidelli & Crida 2007)。そのため、Morbidelli ら (2007) は、木星と土星の研究を拡張し、天王星と海王星を追加しました。彼らは 6 つの共鳴チェーンの可能性を発見しました。そのうち 2 つは 1 億年以上安定していましたが、後に微惑星の円盤によって不安定化する可能性があります。これにより、後に Nice Model 2 と呼ばれる Nice Model が更新されました (Levison ら 2011)。このモデルでは、惑星の初期構成は、円盤段階での惑星移動を考慮した流体力学シミュレーションから取得されました。この新しいバージョンのモデルでは、著者らは、初期条件の広い範囲で不安定性が遅く発生する可能性があることを発見しました。ただし、初期には微惑星円盤が海王星から十分離れており、惑星と微惑星の散乱が起こらないことが条件です。
しかし、それ以来、月への衝突の年代順は修正されています。月への衝突が3.9 Gyr前(つまり、月の形成から6億年後)に激しかったことは事実です。しかし、アポロ計画の余波では、このような激しい衝突は、静止期の後に衝突率が急激に上昇した結果であると考えられていましたが (Tera et al. 1974; Ryder 2000)、月のサンプルの個々の鉱物と月の隕石の衝突年代の新しい分析では、その時期以前には衝突が明らかに少なかったわけではないことが示されています (Zellner 2017 を参照)。月の衝突率の単調な減少は、力学シミュレーション、月のクレーター記録、および月の後期ベニアと一致することが示されています。ただし、月が4.35 Gyr 以前にクレーターと高度に親鉄性の元素の痕跡を失った場合、つまり月のマントルがその時まで部分的に溶融していた場合、そのようになるはずです (Morbidelli 他 2018、Zhu 他 2019、Nesvorný 他 2023)。したがって、3.9 Gyr 前の月の衝突率を説明するために、後期巨大惑星の不安定性を持ち出す必要はありません。ニース モデルの不安定性に関する最も広範な研究は、Nesvorný & Morbidelli (2012) によるものです。その研究で、著者らは、惑星の初期位置、微惑星円盤の位置と質量、および系に最初に存在した惑星の数を含む幅広いパラメータ空間で、惑星の不安定性の統計的研究を行った。今日の木星の軌道励起と、その不規則衛星とトロヤ群小惑星の存在は、この巨大ガス惑星が他の惑星との遭遇を経験したに違いないという証拠を示している。その結果、その惑星は系から簡単に放出される。したがって、系の初期に4つの惑星しか存在していなかった場合、今日の太陽系を再現することはできない。したがって、Nesvorný & Morbidelli (2012) は、最終的に木星によって放出される3番目、さらには4番目の巨大氷惑星が存在する可能性を検討した。ただし、彼らの研究では、惑星の初期位置は、ガス円盤フェーズを模倣した移動処方を使用して設定されている。これにより、共鳴鎖構築のより安価でより広範な調査が可能になりますが、流体力学的シミュレーションのように惑星とディスクの相互作用の複雑さをすべて再現するわけではありません。
ディスクフェーズの終わりにおける巨大惑星の正確な初期構成はわかりませんが、ニースモデルの出発点として、現実的な移動履歴を考慮することが重要です。原始惑星系円盤の物理は、共鳴惑星系の構築にかなりの影響を及ぼします。これまでに引用したすべての研究の時点では、原始惑星系円盤は非常に粘性が高いと考えられていました。しかし、現在では円盤はそれほど乱流ではないと考えられています(理論的議論のレビューについては、Turner et al. (2014) または Lesur et al. (2022) を、観測的制約については Pinte et al. (2016)、Dullemond et al. (2018)、Sellek et al. (2020)、Villenave et al. (2022) を参照してください)。Pierens et al. (2014) の結果に加えて、私たちは最近 Griveaud et al. で次のことを示しました。 (2023) は、低粘性円盤における惑星ペアの移動は、高粘性の場合とは大きく異なることを明らかにしました。木星と土星は、3:2 ではなく 2:1 MMR で固定されています。ただし、Pierens ら (2014) とは異なり、私たちの研究では、この構成でペアの外向きの移動は確認されていません。この結果は、円盤の質量、アスペクト比、および外惑星の初期位置と質量の変更に関して堅牢であることを示しました。前回の論文で述べたように、2 つの研究はエネルギー方程式の扱いと表面密度プロファイルが異なります。これらの違いが、ペアの移動方向の違いを説明できる可能性があります。それでも、前回の研究から、上記のグランド タック シナリオは、太陽系の原始惑星円盤の粘性が低い場合は不可能であると結論付けることができます。しかし、前述のように、グランド タックはもはや必要ないため、低粘性の原始太陽系星雲が考慮される可能性が開かれますが、木星の内側への移動を阻止するメカニズムを見つけることが重要です。したがって、この論文では、Griveaud ら (2023) の結果をニース モデルに拡張することに興味があります。
参考までに、ニース モデルに関するこれまでに引用された研究のほとんどは、木星と土星を 3:2 構成としていました。
一部の研究では、主に学術目的で、木星と土星を 2:1 MMR とする共鳴チェーンをいくつか散発的に検討しました (Nesvorný & Morbidelli 2012、Batygin & Brown 2010、Thommes ら 2008、Pierens ら 2014)。最近では、Clement らが、木星と土星を 2:1 MMR とする共鳴チェーンをいくつか散発的に検討しました。 (2021b,a) は、2 つの惑星の離心率を 0.025 から 0.25 の範囲で調整する 2:1 共鳴における木星と土星の不安定性を広範に研究しました。
しかし、これらの研究はすべて、原始惑星系円盤の物理的性質に関係なく共鳴チェーンを構築し、簡略化された方法で惑星の移動を模倣しました。対照的に、Crida (2009) は、流体力学的シミュレーションを使用して、さまざまな密度プロファイルの粘性円盤内の 4 つの太陽系巨大惑星の移動を研究しましたが、円盤後の段階については取り上げませんでした。私たちの知る限り、Morbidelli ら (2007) だけが、単一の研究で両方の段階を統合し、惑星の移動と巨大惑星の不安定性の間に橋を架けました。彼らの研究と同様に、本論文の目的は、低粘性円盤の文脈で、太陽系の巨大惑星の軌道進化を原始惑星円盤段階から今日の構成まで自己矛盾なく研究することです。まず、そのような円盤で共鳴構成がどのように形成されるか、低粘性がどのようにこれらのシステムの構築に影響を与えるかを調べます。次に、流体力学シミュレーションの出力をニースモデルのN体シミュレーションの初期条件として使用します。
また、Morbidelli ら (2007) は地球全体の不安定性の概念実証 N 体シミュレーションをいくつか示しただけでしたが、私たちは太陽系の再現の成功率を評価します。
この論文は 2 つの主要なセクションに分かれています。セクション 2 では、原始惑星系円盤内の惑星移動の段階について説明します。
まず、セクション 2.1 で流体力学シミュレーションの実行方法について説明します。次に、セクション 2.2 で、2 つの異なる円盤スケールの高さでの 4 つまたは 5 つの惑星の移動の結果を示します。N 体シミュレーションに移行するために、セクション 2.4 でガス円盤の散逸を模倣し、惑星系への影響について説明します。セクション 2.5 では、低粘性円盤での共鳴チェーンの形成に関する「中間的な」結論を示します。論文はセクション 3 に続き、以前に構築された共鳴チェーンからガス ディスクが分散した後の巨大惑星の不安定性段階を研究します。セクション 3.1 で手法を示し、セクション 3.2 で Nesvorný & Morbidelli (2012) の基準に基づいてシミュレーションの成功を評価する方法を説明します。結果はセクション 3.3 で示します。最後に、セクション 4 で完全な研究について説明し、結論を出します。

図 1. 公称シミュレーション N4 におけるディスクの平坦化された表面密度の時間スナップショット。空の円は、木星 (赤)、土星 (青)、天王星 (緑)、海王星 (白) の位置を示します。パネル a は、天王星が土星との 2:1 MMR に入ったことを示しています。パネル b は、海王星が天王星との 3:2 共鳴に固定された瞬間を示しています。パネル c では、4 つの惑星が最終的な共鳴構成 (2:1、3:2、4:3) に入ります。最後に、パネル d は、模擬ディスク分散フェーズの開始時の安定したシステムを示しています (詳細については、セクション 2.4 を参照してください)。これらの瞬間は、図 2 に示されている惑星軌道の進化のスナップショットです。

図 2. 公称シミュレーション N4 における 4 つの惑星の軌道パラメータの進化。網掛け部分は、惑星の近点遠心の位置、それぞれ q = a(1−e) と Q = a(1+e) を示しています。
プロットの始まりの約 150,000 年までは、Griveaud ら (2023) の公称シミュレーション N を示しています。天王星と海王星は、シミュレーションで連続して追加され、最終的な共鳴チェーンは (2:1、3:2、4:3) です。ここで、海王星の導入時間は TN,0 = 250,000 年でした (図 3 を参照)。破線と点線の垂直線は、それぞれ模擬ディスク分散の開始 (t0) と終了 (tf) の時間を示しています。詳細については、セクション 2.4 を参照してください。

図 3。図 2 と同じですが、海王星の導入時間 TN,0 = 238,000 年、つまりシミュレーション Nbis4 です。ここで、天王星は 355,000 年でシステムから排除されます。シミュレーションの後半で、天王星質量の別の氷巨星を追加し、最終的な共鳴チェーン (2:1、2:1、4:3) を取得します。

図 4。図 3 と同じですが、シミュレーション Nbis5 では、天王星質量の氷巨星がシミュレーションに追加され、最終的な共鳴チェーン (2:1、2:1、4:3、5:4) が得られました。このシミュレーションは、ガス ディスク フェーズでは安定していますが、模擬蒸発フェーズでは不安定になります (詳細についてはセクション 2.4 を参照)。

図 5。図 2 と同様に、この図は、より低温のディスク、つまりより低いアスペクト比で進化する 4 つの巨大惑星の軌道パラメータを示しています。シミュレーション C4.2 さらに、図の背景には、シミュレーション全体の時間の関数として、ディスクの方位角平均表面密度プロファイルが表示されています。わかりやすくするために、プロットの左半分には、すべての惑星の軌道パラメータが白で表示されています。プロットの後半では、約 35 万年前から、ガス ディスクの分散フェーズが開始されます。垂直の破線と点線は、このフェーズの開始 t0 と終了 tf を示しています (詳細については、セクション 2.4 を参照してください)。システムは共鳴チェーン (2:1、3:2、5:4) で安定しています。

図 6。図 5 と似ていますが、シミュレーション C5 では、質量 6M⊕ の惑星が追加されています。最終的な共鳴チェーンは (2:1、3:2、5:4、4:3) です。

図 7. シミュレーション C4 における表面密度の半径プロファイルを木星の位置に合わせて再スケールしたもの。青緑色の線は、木星と土星だけが円盤内にあるとき (基本的には Griveaud ら (2023) のシミュレーション) に対応しています。その時点 (t=142 kyr) では、図 5 に示すように、2 つの惑星はゆっくりと内側に移動しています。マゼンタ色の線は、t=308 kyr で 4 つの巨大惑星が外側に移動しているときのプロファイルを示しています。惑星の位置は円マーカーで示されています。垂直の点線は、木星の内側リンドブラッド共鳴 (ILR) と土星の外側リンドブラッド共鳴 (OLR) の位置を示しています (詳細については本文を参照)。

図 8. 外向き移動の場合のガス除去が惑星軌道に与える影響。上図: シミュレーション C4 延長 (実線)、模擬ガス蒸発段階を含む C4 (破線、図 5 に対応)、および C5 (点線、模擬蒸発段階前の図 6 に対応) による木星、土星、天王星、海王星の軌道長半径の進化。下図: 上図で説明した 2 つの C4 ケースにおける木星と土星の離心率の進化。
4. 考察と結論
この研究の目的は、太陽系の巨大惑星の原始惑星円盤段階からニースモデルまでの力学史をたどることです。私たちは、まず完全な流体力学的シミュレーションを使用して共鳴チェーンを構築し、次に模擬円盤蒸発段階の後に、最後の惑星軌道の外側に配置された微惑星円盤と惑星の相互作用を統合することでこれを達成しました。このような完全に一貫した研究は、いわゆるニースモデル2におけるMorbidelliら(2007)とLevisonら(2011)の統合研究以来行われていませんでした。しかし、これらは一方では高粘性の原始惑星円盤という状況で、他方ではニースモデルの後期不安定性の要件で行われました。それ以来、原始惑星系円盤のパラダイムは低粘性円盤へと移行し、不安定性のタイミングに関する制約はなくなりました。そのため、この新しい状況で太陽系の形成の可能性について完全に一貫した研究を行う必要がありました。まず、粘性パラメータ α = 10−4 で 2 次元流体力学シミュレーションを実行し、巨大惑星の収束移動を研究しました。Griveaud ら (2023) で、木星と土星のペアがこのような低粘性円盤で 2:1 MMR を超えることは決してないことをすでに示していました。この系に 2 つの氷巨星を追加し、2 つの異なる円盤スケールの高さに対して 3 つの異なる共鳴チェーンを発見しました。逆境にもかかわらず、5 つの惑星を持つ 2 つの共鳴チェーンも取得しました。最後に、ニース モデル フェーズを研究するために、原始惑星系円盤の蒸発フェーズを模倣し、惑星系がその構成を断熱的に再調整できるようにしました。
この研究の前半は、共鳴チェーンを構築するための流体力学的研究の重要性を示しています。上記の研究を除き、他のすべてのニース モデル研究では、惑星の離心率と半長軸に対する移動の処方または単純な減衰力のいずれかを使用して N 体積分器を使用して構築された共鳴チェーンが使用されています。この研究では、流体力学的シミュレーションで共鳴チェーンを構築することははるかに複雑になる可能性があることを示しています。チェーンの安定性は、惑星の周りのガスの分布に大きく依存します。このような低粘性の円盤では、巨大惑星が広く深いギャップを作成し、共鳴に対するガスの散逸力を大幅に削減します。したがって、低粘性円盤内の複数の巨大惑星のシステムは、特に 3 つ以上の惑星の場合は不安定になりやすい。
私たちが得た 5 つの共鳴チェーンは、ニース モデル研究で以前に研究されたものよりも幅が広い。これは、木星と土星のペアが常に 2:1 MMR にあるためである。2 つのケースでは、2 番目のペアも 2:1 MMR にあり、他のチェーンでは 3:2 にある。以前の研究では、主に学術的な目的で木星と土星を 2:1 MMR で検討していたが、2 番目のペアも 2:1 MMR で検討し、これらのシステムは非常に安定していると結論付けた研究もある (Nesvorný & Morbidelli 2012)。私たちの結果はこの声明と一致しており、シミュレーション Nbis4 と Nbis5 ではほとんど不安定性は見られない。 2 番目の惑星ペアが 3:2 MMR にある場合、文献ではこれらのチェーンが一般に不安定性を引き起こさないことも示されています (Deienno 他 2017; Clement 他 2021b; Nesvorný & Morbidelli 2012)。私たちの結果では、チェーンが冷たい PPD 内に構築されている場合、システムは微惑星ディスクと相互作用するときに非常に不安定になります。30M⊕ ディスクではシステム内のすべての惑星を維持するのに十分ではありませんが、50M⊕ ディスクでは 4 つまたは 5 つの惑星の場合でも成功した結果が得られます。ただし、チェーンが公称 PPD 内に形成される場合、システムはより安定しますが、50M⊕ 微惑星ディスクの場合は多少の不安定性が発生する可能性があります。冷たい原始惑星系円盤で形成される共鳴鎖は、惑星の近傍にガスの減衰効果がないため弱く安定していると考えられ、したがって私たちの結果と、おそらく文献との相違を説明できる。低粘性の状況では、私たちの冷たい円盤と同様にアスペクト比の低い原始惑星系円盤を考慮することが現実的である。また、そのような円盤では、4つの巨大惑星が原始惑星系円盤の段階で外側に移動し、ホットジュピターになることを防いでいることも指摘する。私たちが研究したすべてのシステムの中で、3つの構成が太陽系の制約に適合するために必要な4つの基準をそれぞれ約1%の成功率で満たしており、これはNesvorný & Morbidelli (2012) の最良のケースよりわずかに低いが、同じ桁である。図13では、原始惑星系円盤から現在までのそのような進化の例を示しています。太陽系は一般的な惑星系ではないため、統計的な成功ではなく、シミュレーションから得られる可能性のある結果だけが必要です。したがって、成功率が1%の場合、この研究は太陽系が低粘性の原始惑星系円盤から出現した。現在までに、太陽系の4つの巨星に匹敵する惑星系は発見されていないため、この構成がシミュレーションで最も頻繁に発生する結果である必要はない。結果が微惑星円盤の特性にどのように依存するか(不安定性のタイミングなど)は、この論文の範囲をはるかに超えており、今後の研究の対象となる。

図 13. 太陽系の 4 つの巨大惑星が、低温で粘性の低い原始惑星円盤で形成され、最後の惑星から 0.5 au 離れた 50M⊕ の微惑星円盤と相互作用した場合の、その力学史の考えられるシナリオ。このシナリオでは、初期の惑星系は 5 つの惑星で構成され、5 番目の惑星は P9 に相当する可能性のある 6M⊕ の惑星です。最初の 800 kyr は、惑星が共鳴構成に移行する原始惑星円盤段階の流体力学的シミュレーションを示しています。背景には、円盤内のガス表面密度の半径プロファイルを示しています。次に、模擬ガス分散期間 (2 つの白い破線の間) をシミュレーションします。最後に、惑星が微惑星円盤と相互作用する 1 つの N 体シミュレーションの結果を示します。システムは急速に不安定になり、2 Myr 未満で 5 番目の惑星を放出します。次に、このシステムを数十億年にわたって積分し(x 軸のスケールを線形から対数に変更)、現在の太陽系の良好な類似体を取得します(三角形は巨大惑星の実際の長半径を示します)。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます