2019年1月11日のケンタウルス「ビエノール」による多弦星掩蔽の様子

ケンタウルス（54598）ビエノールの掩蔽観測の結果、直径150±20km　リングは無さそう衛星は位置の関係で地球に影を落とさなかった可能性があるので無いと断言できない。以下、機械翻訳。

2019年1月11日のケンタウルス「ビエノール」による多弦星掩蔽の様子

ABSTRACT 海王星以遠天体やケンタウルスの物理的特性を調べるプログラムの中で、ケンタウルス（54598）ビエノールによる恒星掩蔽が20 19年1月11日に発生し、観測可能性が高いと予測した。高精度な天体観測データを得て予測を精緻化した結果、イベリア半島に有 利な影の道筋が示されました。これに後押しされ、掩蔽観測キャンペーンを実施したところ、4つの観測地点から5つの陽性検出 を得ることができました。ケンタウルス族の多弦（2弦以上）の恒星掩蔽が観測されたのは、これまでに(2060) Chiron, (10199) Chariklo, (95626) 2002 GZ32 の3つで、今回が4つ目です。掩蔽和の解析と掩蔽直後に得られた回転光度曲線から、ビエノールは面積換算直径が であり、150±20kmである。この直径は、熱測定から得られた直径よりも約30km小さい。また、恒星掩蔽の解析から得られた最適 な楕円の短軸の位置角度は、長期測光モデルから得られたスピン軸の位置角度と一致しないことが分かりました。また、回転光 度曲線の極小値のひとつに強い凹凸があり、これは回転光度曲線がどのようなアスペクト角を持つかによらず存在します。 の観測が行われました。異なる手法による結果を調和させるために、異なるシナリオを提示した。リングや衛星の可能性に関連 した二次的な落下は検出されなかった。それにもかかわらず、チャリクロと同じような大きさのリングは、データの精度が低い ため、捨てることができない。 キーワード海王星間天体 - カイパーベルト天体：個体。ビエノール -測光 - 恒星掩蔽

1. はじめに ケンタウルスは、木星と海王星の間の軌道半長軸で太陽 を周回する天体である。動的進化モデルによると、これ らの天体は海王星を越える領域で生まれたが、主に海王 星との惑星衝突の結果、太陽系内側に注入されたことが 分かっている。また、動的シミュレーションによると、3 2個の有名なケンタウルス天体の平均半減期は2.7Myrであ り(Horner et al. 2004)、その生涯のほとんどを海王星超領域で過ごしてい ることになる。このため、ケンタウルス族は、より地球 に近い場所にある小さな海王星以遠天体（TNO）を研究し 、その物理的特性を明らかにする絶好の機会となってい ます。ケンタウルスは、小惑星や彗星などの天体に比べ て、現在の領域での寿命が短いため、化学反応や放射線分 解を受けにくい。したがって、この集団の物理的性質の 研究は、太陽系形成と進化の歴史を再構築するのに重要 な情報を提供する。ここ数年、(10199)Charikloの周りにリング系が発見さ れ、ケンタウルス族への関心が高まっています(BragaRibas et al. 2014)。また、(2060)Ch鉄によるいくつかの恒星掩蔽のデータからも、Charikloで 見つかったものと似た特徴が見つかっていますが、これら の特徴がリングによるものかどうかについては、まだ議論 があります (Ortiz et al. 2015; Ruprecht et al. 2015; Sickafoose et al. 2020)。環状星系の発見は、これらのリングがどのように形成され、これらの小 さなボディの周りでどのように生き残るかを理解するた めの新しい研究分野を開きました。衝突や回転破壊は、 その形成のためのもっともらしいシナリオのようです (Braga-Ribas et al. 2014; Ortiz et al. 2015; Sicardy et al. 2019, and references therein を参照)。さらに、準惑星ハウメアの周りに別の環系 が発見されたこと（Ortiz et al. 2017）は、環が惑星との遭遇によって生存する海王星横 断領域で形成されるかどうかという問題を提起する（こ れはあまりあり得ないとは思えない、Araujo et al.）また、巨大惑星との遭遇による衛星の潮汐破壊とい う説も提案されているが（Hyodo et al.2016）、その可能性は非常に低いと思われる（例えば 、Melita et al.2017）。また、ハウメアの星系（海王星以遠領域で唯一 知られている動的な天体群を含む、Brown et al.2007; Ortiz et al.2012; Proudfoot & Ragozzine 2019; Ortiz et al.2020a) も説明できないでしょう。ただし、これら3つの天体、 Chariklo、Chiron、Haumeaは、いくつかの物理的特性を 共有しています。例えば、いずれも高度に伸長した楕円 形であり、比較的速く回転し、未分離スペクトルには水 の氷が見られます（すなわち、本体とリング、例えば、 以下を参照してください。Barucci et al. 2011; BragaRibas et al. 2014; Duffard et al. 2014b; Ortiz et al. 2017; Cikota et al. 2018; Sicardy et al. 2019; Morgado et al. 2021, and references therein) で、それらの性質が環の存在に関係している可能性が高い です。

E.フェルナンデスバレンズエラら。2019年1月11日のケンタウルス「ビエノール」による多弦星掩蔽の様子 -7 (54598) Bienor は、仮符号 2000 QC243 で、これまでに知られている最大のケンタウルスの一つ で、Chiron や Chariklo のそれよりもわずかに小さい (Braga-Ribas et al. 2014; Ortiz et al. 2015)。その大きさは、Duffardら（2014a）がハーシェル 宇宙望遠鏡（Herschel）の放射性測定値を用いて決定し 、直径198+6 kmが与えられている。その後、Lellouchら(2017) ビエノールのサイズを179〜184±6kmの範囲（モデルや ジオメトリによって異なる）に更新しました。 ALMAのデータ) 1 .また、Bienor はこの2つの天体と楕円形であることや水のようなスペクトルを持つことが共通しています (例えば、Dotto et al. 2003; Rabinowitz et al. 2007; Fernández-Valenzuela et al. 2017）、しかし、その自転周期（約9.14時間）はTNOや ケンタウルス族の平均をわずかに超えています（Thirouin et al. 2014）。これらの の特徴から、Fernández-Valenzuela et al. (2017) は、ビエノールが上記の小天体に見られるようなリング 系を持つ可能性を提唱しています。実際、ビエノールの 経年的な測光データでは、約0.7等という急な輝度上昇と 約0.6等という回転光度曲線の振幅の減少が見られ、リン グモデルと整合的であると思われます。しかし、Fernánd ez-Valenzuela et al. (2017)で検討された他の可能性、例えば静水圧平衡から 外れた非常に細長い天体もかなりよく合います。太陽系 外縁天体による恒星の掩蔽を検出するための国際的 な共同研究において、我々はビエノールが2019年1月11日 th 、ガイアDR2 236278279941456256星を掩蔽すると予測した。これ は、ビエノールの明るさが急激に増加した理由を解明す る絶好の機会となった。最初の予測は、小惑星の運動の 数値積分（NIMA）ソリューション（Desmars 2015; Desmars et al.2015）を用いて行われた。我々は、セクション 2 で説明するように、特別な観測を行い、この予測を改良 した。星掩蔽は4つの観測地点で成功し(セクション3)、 他の4つの地点では星掩蔽がないと報告された。4 章では、データ解析とその結果を報告する。また、ビエ ノールの回転光度曲線を取得し、恒星掩蔽の解釈の助け にしました (5章)。最後に、6節で詳細な解析を行い、7節で結果の考 察を行い、8節で結論を述べます。

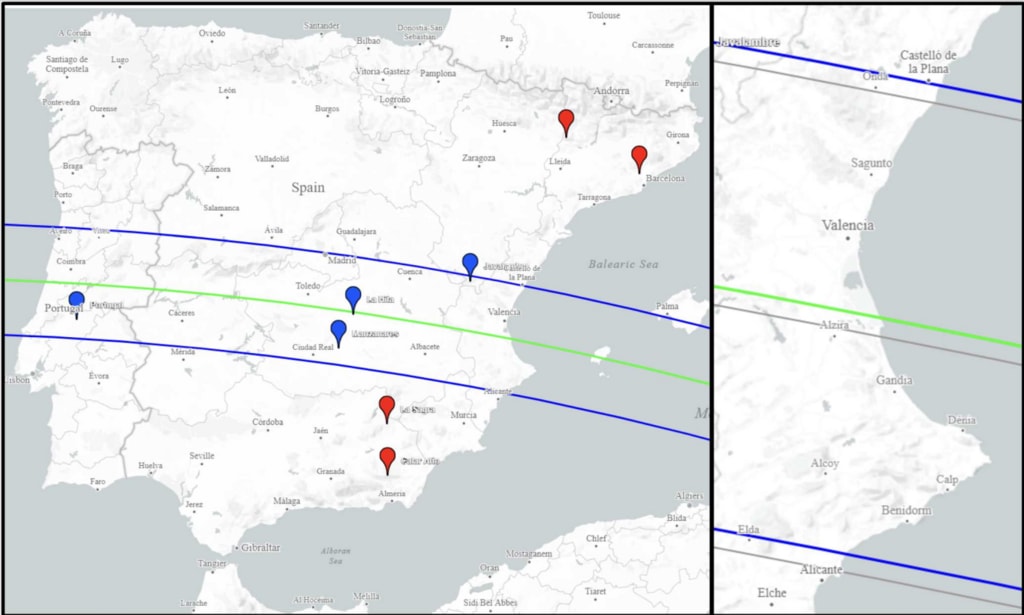
図1：2019年1月11日（th ）にBienorで発生した恒星掩蔽の掩蔽後の影道（青線） を表す地図（緑線が影の中心を表す）。地図上の影道の 幅は、S1 シナリオの適合パラメータからのものである（6 章参照）。影の向きは東から西である。青と赤のタグは 表2の観測所の位置を示しており、青は正検出、赤は負 検出を意味する。右図は、スペイン東海岸を拡大したも ので、予測された影の道（灰色の線）と掩蔽後の影の道 （左図と同じカラーコード）の差、つまり10masの差を 示しています。

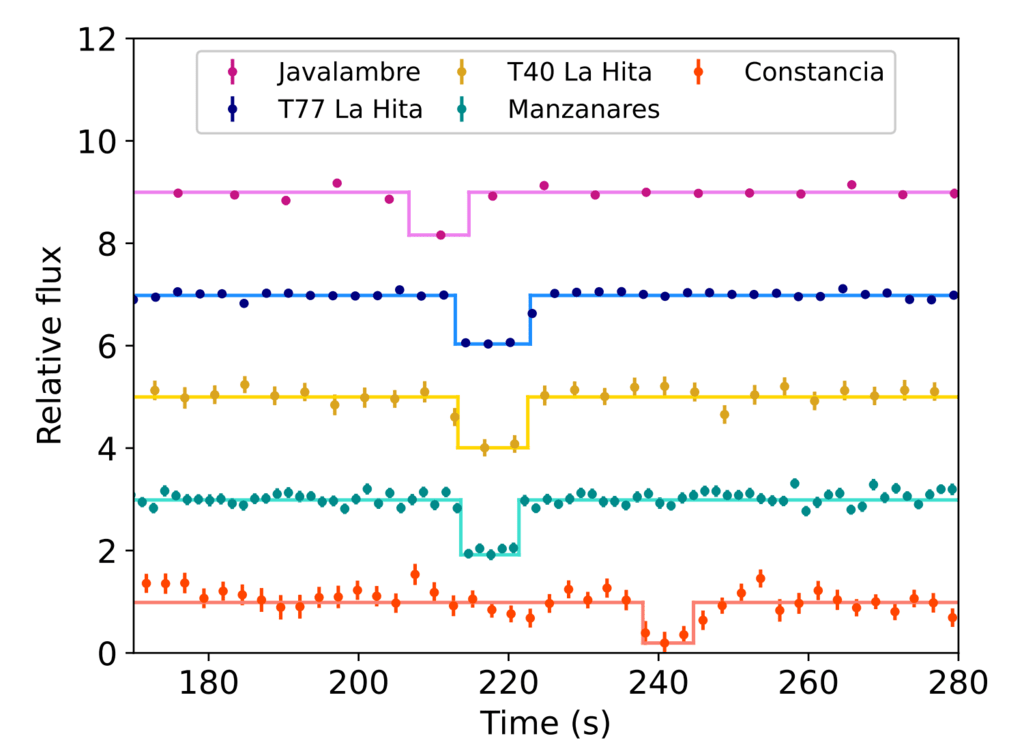
図 2: 影に沿って分布するさまざまな望遠鏡から得られた肯定的な検出を伴う掩蔽光曲線

道。 色の点は不確実性を伴う観測データを表し、線は観測データによく適合する正方形を表します。 時間は 2019 年 1 月 11 日以降の秒数で与えられます

01:00:00 UT。 ライト カーブは 1 つの外側に正規化されています

このプロットでは、掩蔽が低下し、明確にするために任意のオフセットでシフトされます。

図 3: (a) 2014 年、2015 年、2019 年の測光データから得られたロム ピリオドグラム スペクトル パワー。 スペクトルパワーがプロットされます

頻度（サイクル/日）の関数として。 106 の最大スペクトル パワーは 2.61670 サイクル/日で、これは

9.1718時間の回転周期。 (b) 2014 年、2015 年、2019 年の測光データから得られた PDM プロット。 θの最小値が与えられます

2.61669 サイクル/日の頻度 (すなわち、P = 9.17188 h)。

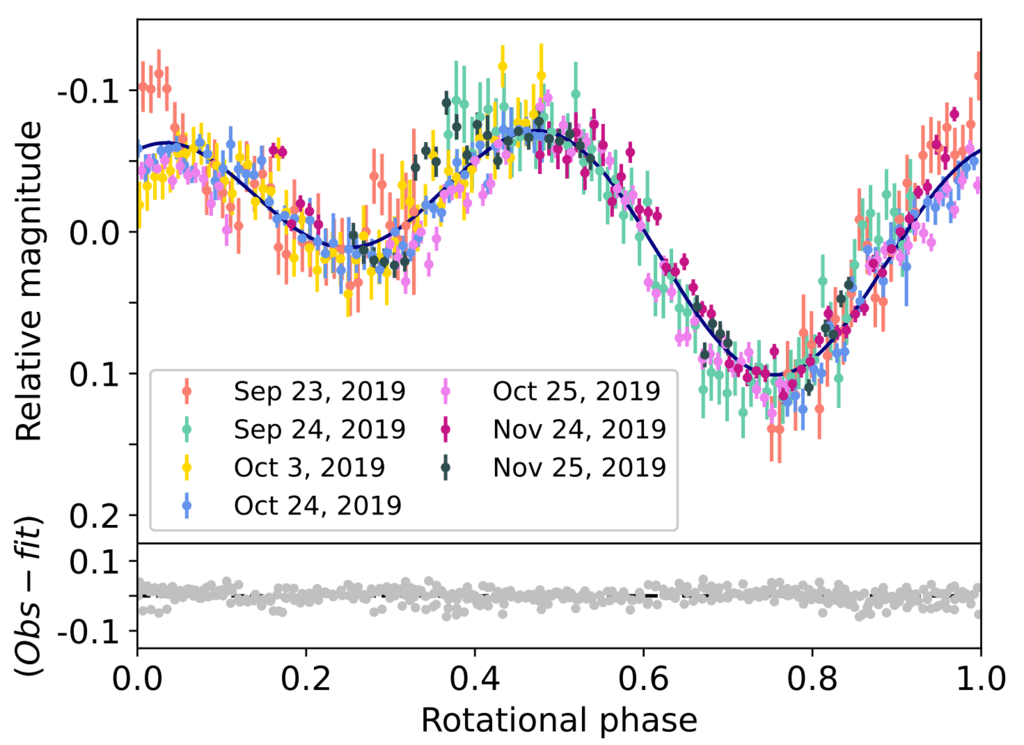
図 4: データを使用して得られた Bienor の回転光度曲線

1.23 m と 1.5 m の望遠鏡から (ここで使用される望遠鏡の詳細な説明については、セクション 5 を参照してください)。 データは

9.1719 ± 0.0002 時間の回転周期を使用して折り畳まれています。

掩蔽時のゼロ回転位相。 違う

によって説明されているように、色は異なる観測夜を表します

伝説。 青い線は二次フーリエ関数を表します

観測データへの適合、ピークから谷までの振幅

fit の値は 0.172 ± 0.003 mag です。 下部パネルで、グレー

ドットは観測データへの適合の残差を表し、標準偏差0.02等。

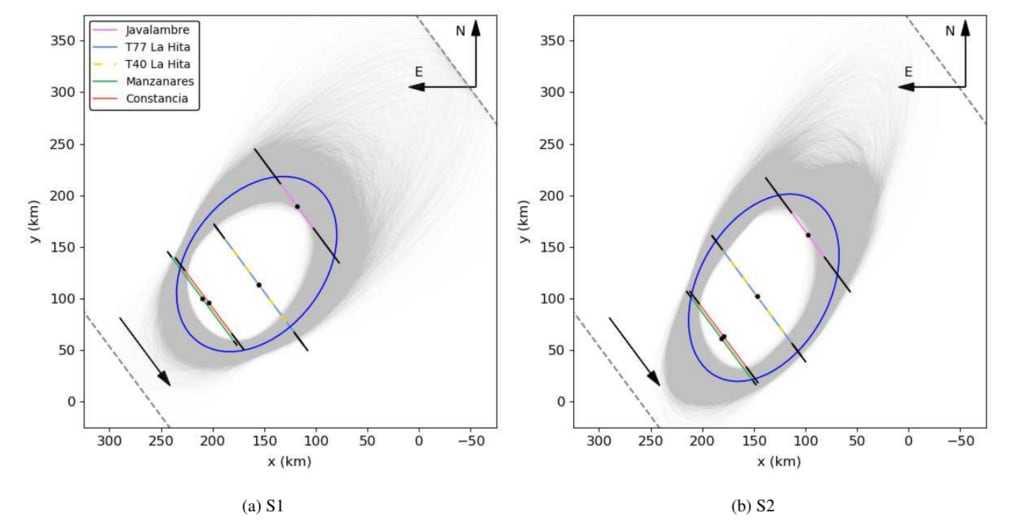
図 5: 図 2 に示す光度曲線から得られた 5 つの掩蔽弦への楕円近似 (x と y は距離を表す)

それぞれ東西方向と南北方向の空平面で。灰色の影付きの領域は、10,000 個の楕円を表します

モンテカルロ法によって与えられ、青色の楕円は最小二乗法による弦の端への最適なフィットを表します

幾何学的距離の最小化。参考までに、コードの色は図 2 のものと一致し、黒い実線が表示されます。

入口/出口時間の1-σの不確実性を表す四肢。 La Hita T40 と T77 のコードは

互いに重なり合っています。楕円の外側の灰色の破線は、最も近い位置 (オブジェクトの北と南) を表します。

Agrupación Astronómica de Sabadell (Sabadell) からのデータに対応する星食が検出されなかった場所

ラ サグラ (グラナダ)。左下隅の黒い矢印は、ケンタウロスに対する星の動きを示しています。 (a) マンサナレスの

弦は、コンスタシアの進入に一致するように移動されます (S1 フィット)。 (b) すべての弦の中心が揃っています (S2 フィット)。

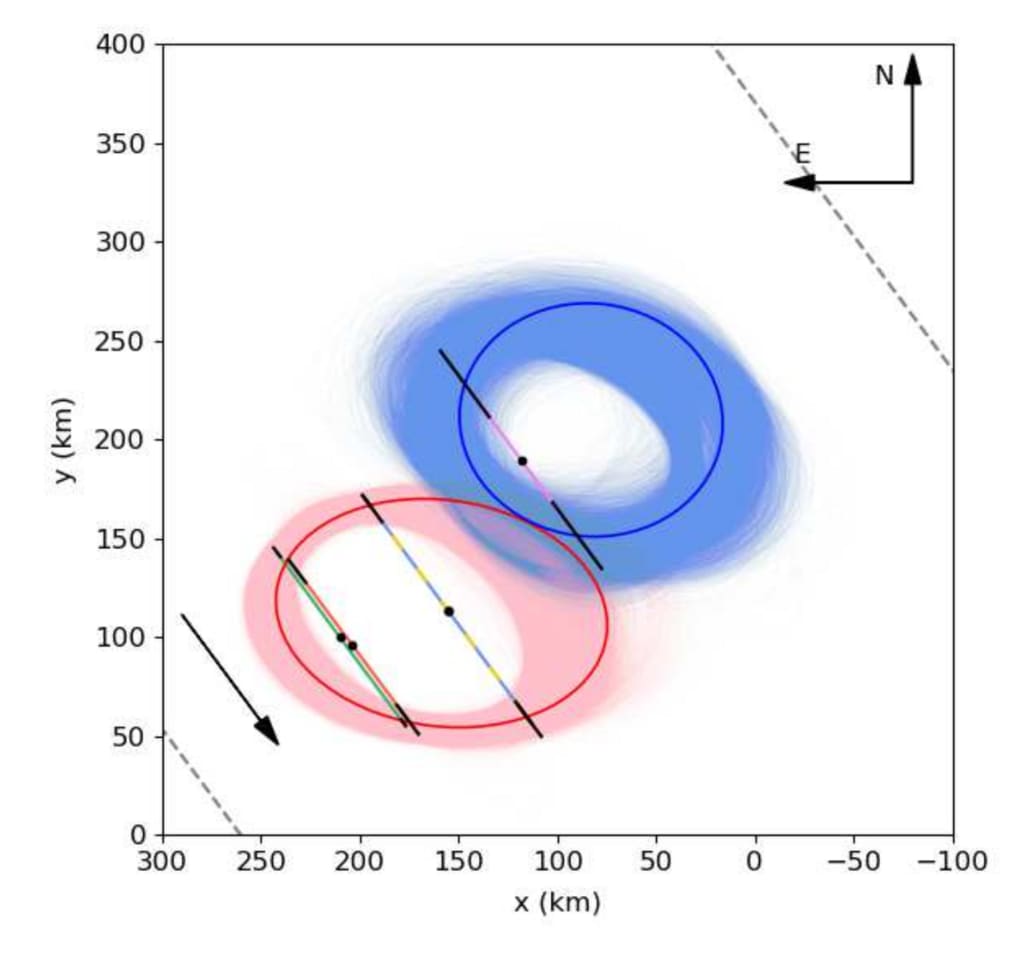
図 6: 2 つの楕円の 5 つの弦への同時適合

図 2 の光度曲線 (x と y は違いを表す)

JPL軌道と影の中心の間。 （シフトなし

マンサナレス以外のコードが適用されています。

コンピュータ同期のエラー)。青と赤

楕円は、χ2 の最小化に関して最適なものを表します。

青と赤の影付きの領域が表す関数

モンテカルロ法によって与えられた 10,000 の可能な解すべて。

参考までに、コードの色は図 2 のものと一致します。

四肢の黒い実線は 1-

σ 入力/出力時間の不確実性。私たちは、ラ・ヒタに注意します

T40 と T77 のコードが重なり合っています。灰色の破線

楕円の外側の線は、最も近い場所を表します (

恒星食があった天体の北と南

Agrupación Astron’omica de Sabadell (サバデル) および La Sagra (グラナダ) からのデータに対応します。の

左下隅の黒い矢印は、影の動きを示しています。

7. ディスカッション

Bienor のサイズを考えると、Bienor が静水圧平衡は合理的であり、その形状は逸脱する可能性があります

3軸楕円体からかなり離れています。 この可能性は、コードがボディに対してやや不規則な形状を示す最初のシナリオ S1 で考慮されます。 ただし、和音のみ

体の 3 つの場所では、いくつかの物理的特性を取得するために、楕円形のフィッティングを実行することに制限されています。 別の可能性としては、Bienor が実際に静水圧平衡にある可能性があります。

したがって、すべてのコードに中心があると予想されます

エラーバー内に整列。 これは、異なる和音間の変位がさまざまな体系的なものによるものであることを意味します。

エラー (コンピューターの同期に関連するエラーなど)。

この可能性は、2 番目のシナリオ (S2) で評価されます。

すべてのコードの中心を揃えました。

ただし、セクション 6 で述べたように、どちらのシナリオでも、熱モデルから得られる直径よりも 30 km 小さい面積相当直径が生成されます。

ルルーシュ等。 (2017)、および 198+6

ダファードらによると-7 km。

(2014b)。この違いが Bienor の回転変調によるものかどうかを知るために、Bienor の回転位相を計算しました。

どの Herschel 測定値が得られたか 6、

セクション 5 で得られた正確な自転周期、および最も近い

は、2014 年に取得されたハーシェル測定に合わせた回転光度曲線を発表しました (Fernández-Valenzuela et al.

2017)。 Herschel と

両方とも同じ回転位相で、最も明るい最小値の間

(図 7 の灰色の垂直線)、推定された不確実性

0.768 h (つまり、回転フェーズで ~ 0.08、図 7の灰色の影付きの領域)。 Herschel の測定値は

最小の明るさで、振幅が小さいためです。

回転光曲線、このサイズの違いは

回転変動。どちらもアスペクト角の変化によるものではありません。

近年増加傾向にある (2014 年から 0.083 ± 0.008 等)。

2019)、これは、オブジェクトが以前の状態から変化していることを意味します。

ポールオン構成からエッジオン構成へ。

一方、はめあいによって提供される位置角度は、

S1 と S2 は、Fernández-Valenzuela らの長期測光モデルの結果と矛盾する可能性があります。 （2017）。

言い換えれば、異なるアスペクト角で得られた光の回転曲線を使用して得られた極の向きは、単一の天体を使用した場合の恒星掩蔽データからの適合結果と互換性がない可能性があります。これは、他のオブジェクトのこの種のモデルの結果であるため、予期しない結果です。

星食によって得られたものと一致します。例えば、

6 Herschel 画像の露出の中間時間: 2011-01-24T12:52:20 および

2011-01-24T22:00:27.

2013年に検出されたカリクローによる恒星食

極方向の 2 組の値: (λp, βp) = (138◦, 28◦)

または (λp, βp) = (26◦, −7◦)、Braga-Ribas et al. を参照。 （2014）。後で、

ダファード等。 (2014a) は、長期測光モデルを使用した解の 1 つを破棄しました (Duffard et al. 2014a の図 1 を参照)。

同様の状況は、カイロンの場合にも現れます。

オリエンテーションは一連の星食によって得られました

そのうちの 1 つは、長期測光データに完全に適合します。

(オルティスら 2015)。近接バイナリ システムは、仮想シナリオです。

これにより、恒星掩蔽の結果を、フェルナンデス・バレンズエラ 他(2017) そして、それはまた、等価直径が大きく、放射計から導出されたものとの互換性が高くなります。接触を形成するまで軌道を縮小する潮汐力によって、システムが相互作用している可能性があると推測できます。

アロコスのために提案された形成シナリオと同様のバイナリ

(McKinnon et al. 2020)、New が訪れた TNO コンタクト バイナリ

2019 年 1 月の Horizons 宇宙船。さらに、このシナリオ

166±9 km の面積相当直径となり、熱測定 (181 ± 8キロ;ルルーシュ等。 2017)。

同期バイナリ システムも Bienor の説明になります。

上で不変の形状を示す回転光曲線。年、振幅の変動は変化に起因する

システムのアスペクト角で。これは別のヒントになるかもしれません

不規則なオブジェクトを破棄します。さまざまなアスペクト角で観察すると、回転光曲線のさまざまな形状が予想されます。両者のスピンと軌道の同期

コンポーネントは、所要時間から合理的な仮定です。

このステータスを達成することは、太陽の時代よりもはるかに小さいです

以下に示すように、システム (1.5 × 10^17 秒)。の

コンポーネントの 1 つが潮汐ロック、tlock、

次の式を使用して取得できます (Hubbard 1984)。

tlock = 2π／3K G a1^3 T0δ(ｄ^6M1/M2^2). (8)

この方程式では、K は永年愛の数であり、

均質な物体の 3/2 の値、G は重力定数、a1 と T0 は長半径と初期回転

最大成分の速度、それぞれ、δ は次のように表されます。

arctan(1/Q) Q = 100 が散逸係数、d が

小さい成分が最大の成分を周回する距離、M1 と M2 は各成分の質量です。

二次が一次を周回する距離は、

次の式から得られます。

d3 = Ts^2G MT/4π ,           (9)

ここで、Ts はセカンダリの軌道周期、MT は

システムの質量。両方の方程式を組み合わせて仮定する

両方のコンポーネントの質量と半径が類似していること (つまり、M1 ≈

M2 = M、および R1 ≈ R2 = R、それぞれ)、システムの時間

潮汐ロックされるには、次から取得できます。

tlock = T4s G M 6π T0K a3 1δ ,   (10)

M = Vρ = 4/3πR3ρ で、R は有効半径、ρ

同じようなサイズのケンタウロスを考慮すると、密度は 700 です。

kg/m−3。したがって、T0 ≥ 9.1718 h (Bienor の回転

現時点での期間):

tlock . 2.5×10^7G、               (11)

これは太陽の年齢よりも桁違いに小さい

システム。

式で与えられる Roche 限界に注意してください。

dR = 2.44a1 ρ1

ρ2 !1/3 ≈ 2.44a1, (12)

a1 = 84 km (S3 E1 から、表 4 を参照)、結果は 205 km、

これは、中心間の距離よりも若干大きい

図 6 で測定された 2 つの物体のうち、d = 150 ± 20 km。ただし、バイナリ フィットは縮退しているため、物体間の距離が大きい別の解が存在します。一方で、

ボディにある程度の内部強度がある場合、コンポーネントは

液体のような物体の公称ロシュ制限よりも近い。

8. 推定環系の限界

リングシステムの存在もより良いマッチングを提供します

恒星の食と熱モデルからの面積等価直径の間。このシナリオを提案したのは、

フェルナンデス・バレンズエラ 他(2017) 似ているから

サイズ、形状、および水っぽいスペクトルでの Bienor の Chariklo および Chiron に対する (まだ議論中ですが、Ortiz et al. 2015;

シカフース等。 2020）。そこに提示された長期測光モデルはかなりうまく機能し、実際、

本体の小さいサイズ用（面積に一致）

この作業で導出された等価直径)、潜在的なので

リングは明るさの大部分に寄与し、

Bienor のスペクトルで水の氷が検出された場合 (例えば、

どっとら。 2003;バークメ等。 2008) として、リングに位置しています。

カリクロの場合 (Duffard et al. 2014a)。主張されている

何人かの著者によると、ケンタウロスは色の二峰性を示し、

非常に赤いオブジェクトとあまり赤いオブジェクトの間で集団を分割する

(Thébault & Doressoundiram 2003; Peixinho et al. 2012)、

それぞれ～8%と～5%のアルベドの中央値(Müller et al.

2020）。絶対等級を使用した研究ではありますが、

観測が行われる位相角の影響を受けません

そのような二峰性を反映していない (Alvarez-Candal et al.

2019）。いずれにせよ、非常に赤くなることと

アルベドはケンタウロスにまだ存在します。 V − R の色で

0.44等 (例えば、Delsanti et al. 2001; Doressoundiram et al.

2002)、Bienor はあまり赤くないケンタウロスの 1 つであり、これは、私たちとは反対に、Bienor のアルベドがやや低いことを示唆しています。

を取得します (表 4 を参照)。 Bienor の周りの水のリングは、本体のアルベドをより小さな値に減少させ、

Fernández-Valenzuela et al。 （2017）。熱データ

ハーシェルからは本体の組み合わせになります

とリングの再放出により、本体の値が大きくなり、

これは、面積相当の違いを説明します

恒星の掩蔽と熱データからの直径。

Bienorが現在、ポールオンの方向に近づいていると仮定します

過去 20 年間の回転光度曲線の振幅の減少のもっともらしい説明として、

推定リングの領域は非常に露出しており、可能性があります

私たちのデータで検出されました。そのため、範囲内で検索しました

Bienor の恒星掩蔽データですが、それらに似た特徴はありません

カリクローとカイロンで発見されました。しかし、その不足は

セカンダリ ドロップの数は、リングやサテライトがないことを証明するものではありません。一方では、衛星を検出する確率

ほんの一握りの和音を持つBienorの周りは無視できます。