天王星の自転軸が傾いてるのは地球クラスの惑星が衝突した説が有力ですが、古代エウロパクラスの衛星が天王星の周辺に有り天王星に吸収されるまで天王星半径の10倍以上移動したら80度天王星の自転軸を傾けられる説です。残り18度はどないすんねんと思いますがニースモデルでは海王星と土星に遭遇していることになってるので、それで傾いたか、足りなければ微惑星の衝突で傾いた事にする。以下、機械翻訳。
太古の衛星の移動による天王星の傾き
2022 年 9 月 21 日提出
環境。天王星の 98° の傾斜角は、惑星形成の最後に発生した巨大な衝突に起因すると一般的に考えられています。ただし、この図には弱点がないわけではありません。
ねらい。木星と土星の衛星の潮汐移動は、10 億年の時間スケールで、それらのスピン軸のダイナミクスに強く影響することが示されています。このメカニズムに照らして、天王星を傾けるシナリオを再検討することを目指しています。
メソッド。天王星の歳差運動スペクトルを分析し、傾斜の原因となる可能性のある永年スピン軌道共鳴の候補を特定します。捕獲に必要な架空の古代衛星の特性を決定し、ダイナミクスを数値的に調査します。
結果。天王星の半径の 10 倍以上移動する場合、最小質量が天王星の質量 4e^-4 の単一の衛星は、天王星をわずかな傾斜角から傾けて 90° に収束させることができます。太陽系の年齢未満で傾斜を達成するためには、衛星の平均ドリフト率が衛星の現在の軌道膨張に匹敵する必要があります。これらの条件下では、シミュレーションは、天王星が容易に 80° 以上傾いていることを示しています。この点を超えると、衛星は非常に不安定になり、惑星の自転軸の無秩序な動きの段階を引き起こします。衛星が惑星に衝突すると、無秩序な段階が終了し、最終的に惑星の傾斜が順行状態または単純な逆行状態 (今日の天王星のように) で凍結します。天王星に似たスピン状態が80%もの確率で得られ、しかし、質量が 1.7e^-3 天王星以上の、より大きな衛星が優先されます。それでも、より小さな古代の衛星が完全に除外されているわけではなく、将来の研究でこの基本的なシナリオを改善する余地があります. いくつかの既存の衛星間の相互作用は有望な可能性です。
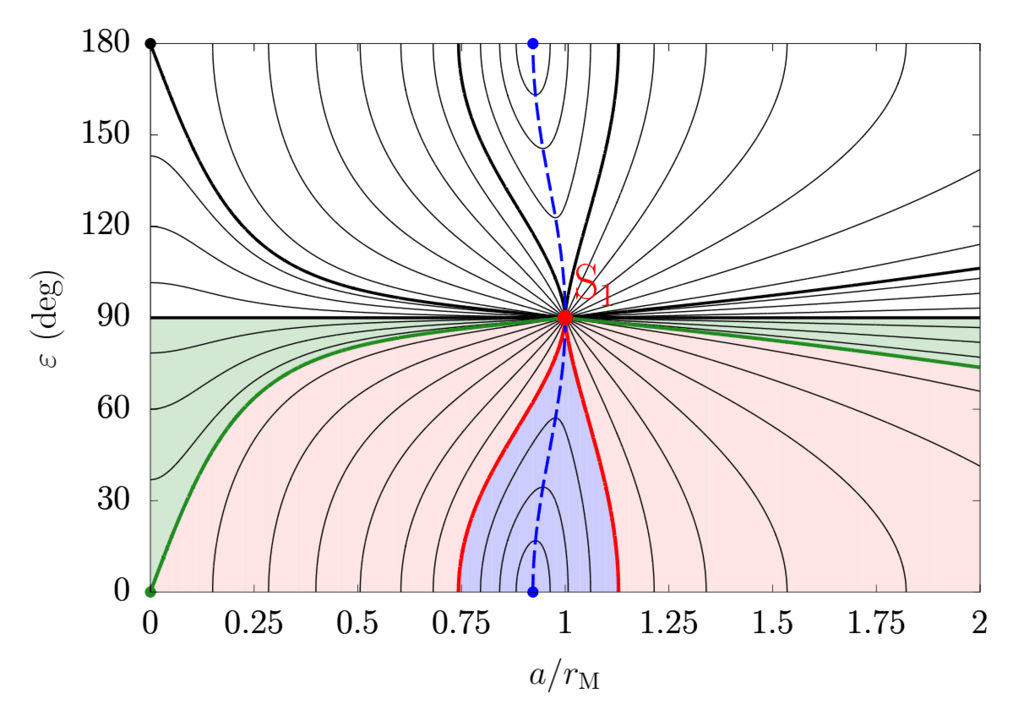
図 1. 惑星のスピン軸歳差運動速度のレベル曲線
その傾きとその衛星の距離の関数。 簡素化された
式の式。 (3) はここでは η = 20 で使用されます。ピンク色の領域の曲線は ε = 0 を結びます。
◦
S1へ。 青い領域の曲線は ε = 0◦ を結びます
に ε = 0◦
また。 緑の領域の曲線は決して ε = 0◦ にはなりません
しかしそれらは S1 に接続します。 ミラー レベル カーブは、逆の歳差運動で ε > 90° に対して存在します。 赤レベルに沿った歳差運動率は
Ω0 = pη/2。 濃い緑色のレベルに沿った歳差運動率は Ω0 = p です。
(a, ε) = (0, 0◦)S1へ。 破線の青い曲線は尾根です
近くと遠くの衛星体制を分ける線。 表情がある
(腕)5 = [pcos2(2ε) + 24 − cos(2ε)]/6. Saillenfest & の図 17 を参照してください。
他の値の η を使用した例については、Lari (2021)。

図 2. 衛星の異なる質量に対する一次永年スピン軌道共鳴の位置と幅。 各パネルで、ラベル付けされた質量 mj
天王星が νj 共鳴に達し、0°から傾くことができるようにするための衛星の最小質量です。
~90°
(表 2 を参照)。 全部の程度
共鳴はピンクで示され、νj 共鳴の中心は赤い曲線で強調表示されます。 終点を分けるおおよその稜線
遠方の衛星体制は、青い破線で示されています(図1と同じ)。 黒い縞模様の領域は、衛星の古典的な領域 E1 です。
ラプラス平面は不安定です。 赤い点は特異点 S1 です。 共鳴は、強制項の周波数 νj によってラベル付けされます (矢印)。
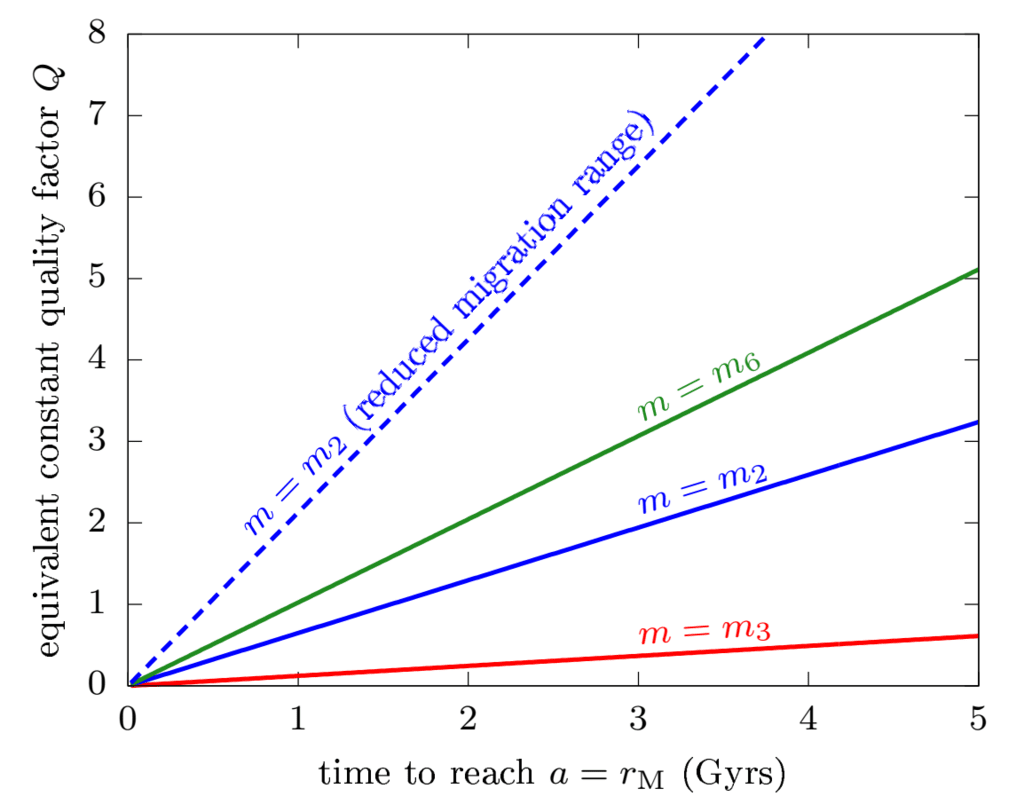
図3 天王星内の潮汐エネルギー散逸のクオリティファクター
衛星が a = 0.8 rM から a = rM に移動するため。 比 k2/Q
は古典的な式から計算され、愛を仮定してここにプロットされます
天王星の数 k2 = 0.1 (Gavrilov & Zharkov 1977)。 質量
衛星のは、曲線の上にラベル付けされています。 比較のために、点線
青い線は、a = 0.96 rM から
a = rM (つまり、移行範囲が ∆a = 2 Req に縮小)、
セクションの数値実験。 3.3.

図 4. 永年スピン軌道共鳴における捕獲と大きな傾斜角への傾斜の例。 衛星の質量と共鳴は次のようにラベル付けされています
数十億年の時間スパンで左から右(黒い点)に移動する数値の軌跡。 衛星の移動タイムスケール τ は
パネル a では 9 Gyrs、パネル b と c では 6 Gyrs。 積分は、ここで使用される数値モデルが失敗するハッチングされた領域で停止します。

図 5. 不安定領域まで傾斜していない共鳴相互作用の例。 シンボルは図4と同じで、衛星は
質量 m3 はすべてのパネルです。 衛星の移動タイムスケール τ は、パネル a、b、および c でそれぞれ 9、2、および 0.2 Gyrs です。

図 6 天王星が傾く確率と衛星の初期傾斜角と移動速度。 各パネルで、パラメーター
規則的なグリッドでサンプリングされ、各パラメータ セットに対して、ランダムな初期スピン軸位相で 240 の数値積分が実行されます。
ψ ∈ [0, 2π)。 カラー マップは、統合中に ε = 80° を超える 240 の軌跡の一部を示しています。 衛星はで初期化されます
a0 = 0.8 rM であり、式 (1) の移行法則で伝播されます。 (9)。 数値積分は、4 Gyrs の後、または衛星がそれを超えたときに停止します
不安定地帯の限界。 衛星の質量は、表 2 の表記を使用して各パネルに表示されます。上部の横軸は、
衛星が a = rM に到達するのに必要な時間。 これは、天王星の実効潮汐係数 Q に変換できます (図 3 を参照)。

図 7. 衛星の離心率が増加する時間スケール
不安定になります。 カラー スケールは、不安定な平衡点で線形化された方程式から計算されるように、離心率が係数 100 で乗算されるのに必要な時間を示します (Tremaine et al. を参照)。
2009; Saillenfest & Lari 2021)。

図 8. 完全結合された永年モデルを使用したシミュレーションの例。
黒と青は、惑星の自転軸に関連する量に使用されます
および衛星の軌道、それぞれ。 永年スピン軌道共鳴角
σ2 = ψ + φ2 です。 衛星の軌道要素は、
日付の赤道と分点を尊重します。 衛星の質量は
m/M = 2.2 × 10^−3
. 衛星はローカルラプラスの近くで初期化されます
a = 37 Reqで平衡し、タイムスケールで外側に移動しました
τ = 6.5 Gyrs。
5. まとめと結論
巨大惑星は原始惑星系円盤の中で形成されると考えられている
ガスとほこりの。最後の形成段階では、ガス降着が最終的なスピン状態を支配し、原始的なほぼゼロの傾斜角を与えます。四大巨人の共通点
太陽系の惑星、特にその自転速度は、このような共通の形成メカニズムを示唆しており、好ましくない可能性があります
主要な形成成分として、ジャイアントインパクトのような確率過程。このビューでは、小から中程度の傾斜
木星の値 (3◦)、土星(27°))、海王星(30°))することができます
形成後の出来事によって説明されます(例えば、ウォードとハミルトンを参照してください
2004;ハミルトン & ウォード 2004;ウォード & カナップ 2006; Vokrouhlický & Nesvorný 2015;ロゴジンスキー & ハミルトン 2020; Saillenfestら。 2021a)。天王星の極端な傾斜を説明する
(98°)はより挑戦的です。あまり影響を与えずに天王星を傾ける
そのスピン速度は、スピ軸の歳差運動を含む遅いプロセスを必要とします。そのようなプロセスは、タイムスパンにほとんど適合しません
初期の太陽系の進化の特定の段階 (例えば、ガス円盤の散逸、または後期の惑星移動) によって提供されます。
これが、天王星の傾きを調査する以前の研究が次のようになっている理由です。
結成後のイベントはタイムスケールの問題に直面しました(ブーエとラスカー2010;キレン等。 2018;ロゴジンスキー & ハミルトン 2021)。
対照的に、衛星の潮汐移動は永遠です。
自然の衛星の軌道をゆっくりと変えることができるプロセス
数十億年。巨大な衛星は、惑星のスピン軸運動に影響を与えることが知られています (例えば Tremaine 1991; French et al.
1993; Boué & Laskar 2006)、および太陽電池の寿命
木星と土星の主要な衛星のシステム移動は、それらの衛星に劇的な傾斜の変化を潜在的に生み出す可能性があります。
ホスト惑星 (Saillenfest et al. 2020, 2021b)。この記事では、このメカニズムが天王星にも適用できるかどうかを調べました。
おそらくその極端な傾斜を説明します。
ここで考えられるメカニズムには、永年スピン軌道が含まれます
共鳴、つまり、歳差運動間の共鳴
惑星のスピン軸とその軌道の歳差運動に現れるいくつかのハーモニクス。衛星として2つの異なるフェーズで構成されています
移動: i) 共鳴の捕捉と安定した傾斜角の増加、
ii) 傾斜角が 70 度を超えると、衛星が激しく不安定化します。
~80°
(Saillenfest & Lari 2021)。両方のフェーズ
衛星の特性を決定するために使用できます。
天王星の現在のスピン状態を再現するために必要です。
フェーズ 1: 非常に遅いプロセスを研究しており、天王星の軌道は何十億年もの間安定しているため、次のことを行う必要があります。
天王星の現在の軌道ダイナミクスを、
そのスピン軸運動。これにより、可能性に強い制約が課せられます。
永年スピン軌道共鳴が関与しています。軌道強制項
天王星のスピン軸の歳差運動率に最も近いものには周波数があります
ν15 = g7 − g8 + s7 (ここで、gj と sj はアプシダルとノード1 から数えた太陽系惑星の歳差運動モード
水星の場合は海王星の場合は 8 まで)。共鳴を生み出すために
ν15 の場合、天王星には最小質量の衛星があったに違いありません
m/M = 3.5 × 10^−4
(当時、天王星に衛星が 1 つあったと仮定すると);ただし、この共鳴は弱すぎて許可できません
の年齢未満での断熱捕獲と傾斜のために
太陽系。 2 番目に近い強制項には頻度があります
ν3 = s8。 ν3との共鳴を引き起こし、天王星を上に傾ける
大きな傾斜にするには、最小質量の衛星が必要です
m/M = 4.4×10^−4
、つまり、m ≈ 4×10^22 kg (木星よりも小さい)
衛星のエウロパ)。シミュレーションは、天王星がこの共鳴で捕捉されて傾く確率が 100% であることを示しています。
衛星移動率の広い間隔と原始
0◦ の間の傾き εと 20◦傾斜を完了するには
フェーズでは、衛星は約 10 半径の範囲にわたって移動する必要があります。
その歴史の中での天王星。この距離を
太陽系の年齢は、衛星が移動する必要があります
少なくとも6cm/ yr
平均して。この移行率は、過去のモデルから推測できるものよりも桁違いに高い
天王星内の潮汐消散のタイタンで測定された 11 cm/yr (Lainey et al. 2020 を参照)。 Fullerらによって説明されたものと同様のメカニズム。 (2016)は
天王星の周りの急速な衛星拡大の実行可能な説明。
m/M の質量 = 4.4 × 10^−4
天王星の現在の衛星の総質量の約 4 倍です。これは、
関連する衛星はもはや存在せず、存在していたに違いありません
進化の第 2 段階で破壊されました。より大規模な古代の衛星は、他の共鳴に到達することを可能にします。
最も強い共鳴は ν2 = s7 で、衛星の質量 m/M = 2.2 × 10^−3 で到達できます。
.他の有望な共鳴候補は、ν7 = g5 − g7 + s7 および ν5 = −g5 + g6 + s6 であり、到達可能です。
質量 m/M = 1.3 × 10^−3
および 1.7 × 10^−3、それぞれ(つまり木星の衛星カリストとガニメデの質量の間)。
これらの質量推定値は、単一の古代衛星に当てはまります。天王星の場合
当時、追加の内側の衛星系がありました。必要な質量が減少します。たとえば、天王星の現在の衛星と仮想の古代衛星を一緒に配置すると、
システム、上記のすべての質量推定値はで割る必要があります
およそ 2 倍です。
フェーズ 2: 衛星の軌道と
惑星のスピン軸ダイナミクス。システムが
不安定なゾーン、衛星の軌道は非常に急速に興奮する可能性があります
離心率と傾きのほぼすべての値に到達します。もしも
衛星は十分に巨大で、その野生の軌道変動が惑星の自転軸に逆反応を引き起こします: 惑星は掃引します
さまざまな永年スピン軌道共鳴を超えて、不規則な傾斜キックを受けます。これらのキックにより、惑星は大きく動くことができます
不安定な領域でより深くなり、今日の天王星と同様の傾斜角に達します。遅かれ早かれ衛星は
ロシュ限界(または惑星に衝突)、
混沌としたダイナミクスと、最後の惑星の自転を化石化する
州。衛星の衝突は、経年変化の作用によって発生します
赤道傾斜角に位置する共鳴 2ω+ Ω IQ ≈ 56◦
、 と
IQ ≈ 124◦ でその対称対応する 2ω − Ω に
.この共鳴は人工衛星でよく知られています (例えば、Daquin et al.
2022年)。惑星の傾き ε = 90° では消えるので
、 衛生
衝突は、惑星の傾斜角が 90 度よりかなり大きい場合にのみ発生します。
(今日の天王星のように)、またはかなり小さい
90°以上
.興味深いことに、天王星の現在の状態は、
ε > 90◦ におけるヒストグラムの最大値
側。これはあるかもしれません
ここで提案されたメカニズムの支持。
より大きな共鳴とより大規模な衛星が生み出す
より強い斜めキック。私たちのシミュレーションは、m/M = 4.4×10^−4
、衛星は一般的に傾斜が80°に達する前に惑星に衝突します。
.そのため再現は難しいようです
共鳴ν3での捕捉による天王星の現在の状態、
この共鳴が素晴らしい捕獲と傾斜を示したとしても
効率。を生成する可能性のある他の現象について説明しました。
そのような小さな古代の衛星の余分な傾き (例えば、小惑星とのその後の衝突) を見逃していましたが、満足のいくものではありませんでした。
より大規模な衛星は、天王星の現在のスピン状態を再現することにはるかに成功しています。衛星に質量がある場合
m/M 2 ~ 3 × 10^−3、成功の確率 共鳴 ν2 での捕捉は 86% にもなります。わずかに
より小さな質量 (m/M ≈ 1.5 ~ 2 × 10^−3)、共鳴 ν5 と ν7
また、成功率が高く、50% に達するものもあります。
パラメータの範囲。以前のように、天王星がすでに追加のセットを持っていると仮定すると、これらの質量推定値を減らすことができます
当時の内月。しかし、彼らの生存は保証されていません。
共鳴 ν2 は、天王星自身のノードの歳差運動モード s7 との永年スピン軌道共鳴であるため、特別です。そのため
幅が大きいと、衛星を非常に早い段階で不安定にする可能性のある傾斜の大きな振幅の振動が生成されます。
フェーズ 1 の短い通過。さらに、レゾナンス ν2 は非常に強力なキックを生成し、傾斜をすばやく上昇させることができます。
天王星の現在の値に。このため、私たちのシミュレーションは、
衛星が適切な距離で初期化されている限り
(a0 ≈ 50 Req)、共鳴 ν2 を介した傾斜メカニズムは、非常に小さな移動範囲 (代わりに数 Req のみ) まで動作できます。
一般的なケースでは 10 の要件)。の成り立ちを勉強するとき、
Mosqueira & Estrada (2003a,b) は、ガス状の惑星周円盤にある木星、土星、天王星の主要な衛星から、次のことを発見しました。
約 50 Req の距離は、まさに人が期待する場所です。
天王星の周りに形成される巨大な衛星。天王星の現在の主な衛星(ミランダ、アリエル、ウンブリエル、チタニア、オベロン)
巨大惑星の他の衛星と比較して、それらは非常に小さく見えるかもしれません。これらの議論から、少なくとも質量のある衛星を形成すると主張するかもしれません。
比 m/M ≈ 2 × 10^−3
a0 ≈ 50 の距離では Req は見えません
衛星形成理論の文脈ではあまりにも不合理です。
成功した傾斜シナリオは、単に再現するだけではありません。
天王星の現在のスピン状態だけでなく、その存在も可能にします
観測衛星システム。
天王星の今日の主な衛星は、
軌道を順行し、それらは軌道に形成された兆候を示しています
潮汐ディスク (Crida & Charnoz 2012)。可能性について話し合った
天王星の架空の古代衛星の破壊によって生成されたデブリディスクから形成された.
ロシュの制限を下回っています。新世代の形成
衛星は、他の動的プロセスと比較して非常に高速であると予想されます。次に、生まれたばかりの衛星が必要になります
同期軌道から外側に移動する (a ≈ 3.4 Req)
現在の距離まで (Oberon は ≈ 23 Req です)。そのような
従来の潮汐モデルのコンテキストでは、大きな移動範囲は非現実的に見えますが、10億年で達成できる可能性があります
タイタンについて最近提案された「潮汐ロック」と同様のメカニズムが天王星の衛星にも作用している場合のタイムスケール (フラー
ら。 2016;レイニー等。 2020).しかし、これが事実である場合、衛星は、Crida & Charnoz (2012) によって記述された特異な分布に従う特別な理由はありません。
潮汐ディスクの起源。私たちの間の可能な関係
提案された古代の衛星と現在のものは、したがって、
簡単な質問です。
さらに、天王星のスピン状態をうまく再現したシミュレーションのサブセットでは、古代の
衛星が逆行しているときにほとんど常に発生します (IQ ≈ 124◦)。したがって、単純化された長期モデルでは提供されません。
そのから順行潮汐ディスクを生成する簡単な方法
破片、破砕プロセスをモデル化する必要があります
ディスクの特性を評価するための詳細 – 潮汐を含む
衛星内の散逸、軌道および衝突進化
破片の、およびからの追加の噴出物の可能性
星。
これらの問題は、天王星の現在の衛星が原始的であり、同じ気体で形成されていると考えると解決されます
私たちの架空の古代衛星としてのディスク (つまり、Mosqueira & Estrada 2003a,b のシナリオに従う)。明確ではありませんが、
現在の衛星が生き残ったかどうか
それらの大規模な隣人の激しい不安定な段階、およびかどうか
彼らは今日と同じように軌道を非興奮状態に保っていたでしょう。
その後、離心率は潮の散逸によって減衰する可能性があります。
しかし、傾斜は減衰時間スケールがはるかに長くなります。この問題の可能な解決策は、現在の衛星が傾斜中に天王星に近かったことを考慮することです。
その赤道面にしっかりと固定されており、それらが実質的に
その後移住。これらのシナリオには複数の月が含まれるため、
N体シミュレーションを使用してそれらを調査する必要があります
明確な答えを得る。
私たちの結果は、実行された数値探査に基づいています
経年モデルで。の任意の値に対して高速で有効であること
偏心と傾斜、これらのモデルにより、
膨大なパラメータ。進化の第一段階では、
質的に正確な画像を提供することが保証されています。
逆に、第 2 段階では、衛星の離心率が 1 に近づき、歳差が
とても早い。衛星の正確な最終的な運命と潮汐ディスクの特性を決定するには、さらに多くの作業が必要です。
それは作成します。この極端な動的レジームでは、平均化されていない
おそらく数値積分が必要です。
潮汐散逸の影響はまだ調査していません
サテライト内。再び、潮の散逸が影響を与えるだろう
進化の第 2 段階で、衛星の離心率が大幅に増加します。不安定化プロセスの正確な結果を先験的に予測することは困難です。
競合する効果: 惑星内の潮汐散逸 (外向きの衛星移動を生み出す)、動的不安定化
(離心率を増加させる)、および内の潮の散逸
衛星(軌道を円形化し、内側に
移行)。衛星への正味の影響は、以下に大きく依存します。
これら 3 つの競合する効果の相対的なタイムスケール。
でのエネルギー散逸の特定のメカニズムに関連しています。
遊ぶ。巨大氷惑星内部の消散過程は今日では本質的に知られていないため、天王星の内部組成は
古代の衛星は非常に投機的であるため、取得しようとはしませんでした。
ここで明確な答え。ただし、私たちの結果はロバストとして役立ちます
今後の実験の出発点: レベルに応じて
衛星内の潮汐散逸、我々は3つの異なることを期待することができます
挙動: i) 散逸が非常に強い場合、衛星の不安定化は抑制され、我々のシナリオは天王星のスピン状態を再現できません。
ii) 散逸が中程度、不安定化は遅れるかもしれませんが、抑制されません。これにより、1回の実行で成功する割合が増加する可能性があります
小型衛星、質量 m/M ≈ 4.4 × 10^−4 まで
; iii) 散逸が小さい場合、ここで概説した図は変化しません。この記事では、基本的な成分をまとめました。
太古の衛星の移動を介して天王星の現在の状態を再現することができます。このシナリオには洗練のために余地があります
。 1つの有望なバリアントは、2つを呼び出すことです
衛星: 遠くにある大きな衛星 (ここで説明したもの) と小さな衛星
1 つは天王星に非常に近い位置にあります。この構成では、内側の衛星は潮汐移動をはるかに起こしやすくなります。
外側のもの;内側のサテライトが外側に移動する間
数回の Req で、外側の方は効果の変化を感じるでしょう。
天王星の J2 パラメータ。これにより、その特性半径 rM が増加します。その結果、傾斜機構全体は次のようになります。
たとえ遠くの大きな衛星が移行する必要はまったくありません。このバリアント シナリオは、
大きなエネルギーの両方で制約を緩和することが可能です
天王星の内部で必要な散逸(近くの衛星は、より少ないエネルギー散逸を必要とします。遠くのものの移動)、および移動に必要な大きな質量について
古代の衛星(いくつかの適度に組み合わされたアクションとして)大規模な衛星でも同じ効果が得られます)。探検
これと他の可能なバリアント シナリオのうち、将来のために残されます。
動作します。
上記の未回答の質問にもかかわらず、この新しい
天王星の傾斜の写真は、私たちにとって非常に有望に見えます.
私たちの知る限りでは、これは初めての単一のメカニズムです。
天王星を傾ける (フェーズ 1) ことと、その回転軸を化石化することができます。
巨大な衝撃を引き起こすことなく、最終的な状態 (フェーズ 2) で、または
その他の外的現象。成功した実行の大部分はピークに達します
天王星の位置で、これは天王星の自然な結果として現れる
ダイナミクス。この図は、一般的な現象としても魅力的です。今日、木星は傾斜段階を開始しようとしています (Saillenfest et al. 2020)、土星はその中間にある可能性があります (Saillenfest et al.
2021b)、そして天王星は最終段階を完了し、その衛星の破壊.この写真を観察に直面させることは簡単な作業ではありません.
答えの一部は、天王星の現在の衛星の潮汐移動速度の尺度によって与えられます。高い率は、それらが天王星のかなり近くで形成されたことを示します。
それらが古代の衛星の破片から形成された可能性、またはそれらがその野生の不安定化段階から保護された可能性を与えます.
太古の衛星の移動による天王星の傾き
2022 年 9 月 21 日提出
環境。天王星の 98° の傾斜角は、惑星形成の最後に発生した巨大な衝突に起因すると一般的に考えられています。ただし、この図には弱点がないわけではありません。
ねらい。木星と土星の衛星の潮汐移動は、10 億年の時間スケールで、それらのスピン軸のダイナミクスに強く影響することが示されています。このメカニズムに照らして、天王星を傾けるシナリオを再検討することを目指しています。
メソッド。天王星の歳差運動スペクトルを分析し、傾斜の原因となる可能性のある永年スピン軌道共鳴の候補を特定します。捕獲に必要な架空の古代衛星の特性を決定し、ダイナミクスを数値的に調査します。
結果。天王星の半径の 10 倍以上移動する場合、最小質量が天王星の質量 4e^-4 の単一の衛星は、天王星をわずかな傾斜角から傾けて 90° に収束させることができます。太陽系の年齢未満で傾斜を達成するためには、衛星の平均ドリフト率が衛星の現在の軌道膨張に匹敵する必要があります。これらの条件下では、シミュレーションは、天王星が容易に 80° 以上傾いていることを示しています。この点を超えると、衛星は非常に不安定になり、惑星の自転軸の無秩序な動きの段階を引き起こします。衛星が惑星に衝突すると、無秩序な段階が終了し、最終的に惑星の傾斜が順行状態または単純な逆行状態 (今日の天王星のように) で凍結します。天王星に似たスピン状態が80%もの確率で得られ、しかし、質量が 1.7e^-3 天王星以上の、より大きな衛星が優先されます。それでも、より小さな古代の衛星が完全に除外されているわけではなく、将来の研究でこの基本的なシナリオを改善する余地があります. いくつかの既存の衛星間の相互作用は有望な可能性です。
図 1. 惑星のスピン軸歳差運動速度のレベル曲線
その傾きとその衛星の距離の関数。 簡素化された
式の式。 (3) はここでは η = 20 で使用されます。ピンク色の領域の曲線は ε = 0 を結びます。
◦
S1へ。 青い領域の曲線は ε = 0◦ を結びます
に ε = 0◦
また。 緑の領域の曲線は決して ε = 0◦ にはなりません
しかしそれらは S1 に接続します。 ミラー レベル カーブは、逆の歳差運動で ε > 90° に対して存在します。 赤レベルに沿った歳差運動率は
Ω0 = pη/2。 濃い緑色のレベルに沿った歳差運動率は Ω0 = p です。
(a, ε) = (0, 0◦)S1へ。 破線の青い曲線は尾根です
近くと遠くの衛星体制を分ける線。 表情がある
(腕)5 = [pcos2(2ε) + 24 − cos(2ε)]/6. Saillenfest & の図 17 を参照してください。
他の値の η を使用した例については、Lari (2021)。

図 2. 衛星の異なる質量に対する一次永年スピン軌道共鳴の位置と幅。 各パネルで、ラベル付けされた質量 mj
天王星が νj 共鳴に達し、0°から傾くことができるようにするための衛星の最小質量です。
~90°
(表 2 を参照)。 全部の程度
共鳴はピンクで示され、νj 共鳴の中心は赤い曲線で強調表示されます。 終点を分けるおおよその稜線
遠方の衛星体制は、青い破線で示されています(図1と同じ)。 黒い縞模様の領域は、衛星の古典的な領域 E1 です。
ラプラス平面は不安定です。 赤い点は特異点 S1 です。 共鳴は、強制項の周波数 νj によってラベル付けされます (矢印)。

図3 天王星内の潮汐エネルギー散逸のクオリティファクター
衛星が a = 0.8 rM から a = rM に移動するため。 比 k2/Q
は古典的な式から計算され、愛を仮定してここにプロットされます
天王星の数 k2 = 0.1 (Gavrilov & Zharkov 1977)。 質量
衛星のは、曲線の上にラベル付けされています。 比較のために、点線
青い線は、a = 0.96 rM から
a = rM (つまり、移行範囲が ∆a = 2 Req に縮小)、
セクションの数値実験。 3.3.

図 4. 永年スピン軌道共鳴における捕獲と大きな傾斜角への傾斜の例。 衛星の質量と共鳴は次のようにラベル付けされています
数十億年の時間スパンで左から右(黒い点)に移動する数値の軌跡。 衛星の移動タイムスケール τ は
パネル a では 9 Gyrs、パネル b と c では 6 Gyrs。 積分は、ここで使用される数値モデルが失敗するハッチングされた領域で停止します。

図 5. 不安定領域まで傾斜していない共鳴相互作用の例。 シンボルは図4と同じで、衛星は
質量 m3 はすべてのパネルです。 衛星の移動タイムスケール τ は、パネル a、b、および c でそれぞれ 9、2、および 0.2 Gyrs です。

図 6 天王星が傾く確率と衛星の初期傾斜角と移動速度。 各パネルで、パラメーター
規則的なグリッドでサンプリングされ、各パラメータ セットに対して、ランダムな初期スピン軸位相で 240 の数値積分が実行されます。
ψ ∈ [0, 2π)。 カラー マップは、統合中に ε = 80° を超える 240 の軌跡の一部を示しています。 衛星はで初期化されます
a0 = 0.8 rM であり、式 (1) の移行法則で伝播されます。 (9)。 数値積分は、4 Gyrs の後、または衛星がそれを超えたときに停止します
不安定地帯の限界。 衛星の質量は、表 2 の表記を使用して各パネルに表示されます。上部の横軸は、
衛星が a = rM に到達するのに必要な時間。 これは、天王星の実効潮汐係数 Q に変換できます (図 3 を参照)。

図 7. 衛星の離心率が増加する時間スケール
不安定になります。 カラー スケールは、不安定な平衡点で線形化された方程式から計算されるように、離心率が係数 100 で乗算されるのに必要な時間を示します (Tremaine et al. を参照)。
2009; Saillenfest & Lari 2021)。

図 8. 完全結合された永年モデルを使用したシミュレーションの例。
黒と青は、惑星の自転軸に関連する量に使用されます
および衛星の軌道、それぞれ。 永年スピン軌道共鳴角
σ2 = ψ + φ2 です。 衛星の軌道要素は、
日付の赤道と分点を尊重します。 衛星の質量は
m/M = 2.2 × 10^−3
. 衛星はローカルラプラスの近くで初期化されます
a = 37 Reqで平衡し、タイムスケールで外側に移動しました
τ = 6.5 Gyrs。
5. まとめと結論
巨大惑星は原始惑星系円盤の中で形成されると考えられている
ガスとほこりの。最後の形成段階では、ガス降着が最終的なスピン状態を支配し、原始的なほぼゼロの傾斜角を与えます。四大巨人の共通点
太陽系の惑星、特にその自転速度は、このような共通の形成メカニズムを示唆しており、好ましくない可能性があります
主要な形成成分として、ジャイアントインパクトのような確率過程。このビューでは、小から中程度の傾斜
木星の値 (3◦)、土星(27°))、海王星(30°))することができます
形成後の出来事によって説明されます(例えば、ウォードとハミルトンを参照してください
2004;ハミルトン & ウォード 2004;ウォード & カナップ 2006; Vokrouhlický & Nesvorný 2015;ロゴジンスキー & ハミルトン 2020; Saillenfestら。 2021a)。天王星の極端な傾斜を説明する
(98°)はより挑戦的です。あまり影響を与えずに天王星を傾ける
そのスピン速度は、スピ軸の歳差運動を含む遅いプロセスを必要とします。そのようなプロセスは、タイムスパンにほとんど適合しません
初期の太陽系の進化の特定の段階 (例えば、ガス円盤の散逸、または後期の惑星移動) によって提供されます。
これが、天王星の傾きを調査する以前の研究が次のようになっている理由です。
結成後のイベントはタイムスケールの問題に直面しました(ブーエとラスカー2010;キレン等。 2018;ロゴジンスキー & ハミルトン 2021)。
対照的に、衛星の潮汐移動は永遠です。
自然の衛星の軌道をゆっくりと変えることができるプロセス
数十億年。巨大な衛星は、惑星のスピン軸運動に影響を与えることが知られています (例えば Tremaine 1991; French et al.
1993; Boué & Laskar 2006)、および太陽電池の寿命
木星と土星の主要な衛星のシステム移動は、それらの衛星に劇的な傾斜の変化を潜在的に生み出す可能性があります。
ホスト惑星 (Saillenfest et al. 2020, 2021b)。この記事では、このメカニズムが天王星にも適用できるかどうかを調べました。
おそらくその極端な傾斜を説明します。
ここで考えられるメカニズムには、永年スピン軌道が含まれます
共鳴、つまり、歳差運動間の共鳴
惑星のスピン軸とその軌道の歳差運動に現れるいくつかのハーモニクス。衛星として2つの異なるフェーズで構成されています
移動: i) 共鳴の捕捉と安定した傾斜角の増加、
ii) 傾斜角が 70 度を超えると、衛星が激しく不安定化します。
~80°
(Saillenfest & Lari 2021)。両方のフェーズ
衛星の特性を決定するために使用できます。
天王星の現在のスピン状態を再現するために必要です。
フェーズ 1: 非常に遅いプロセスを研究しており、天王星の軌道は何十億年もの間安定しているため、次のことを行う必要があります。
天王星の現在の軌道ダイナミクスを、
そのスピン軸運動。これにより、可能性に強い制約が課せられます。
永年スピン軌道共鳴が関与しています。軌道強制項
天王星のスピン軸の歳差運動率に最も近いものには周波数があります
ν15 = g7 − g8 + s7 (ここで、gj と sj はアプシダルとノード1 から数えた太陽系惑星の歳差運動モード
水星の場合は海王星の場合は 8 まで)。共鳴を生み出すために
ν15 の場合、天王星には最小質量の衛星があったに違いありません
m/M = 3.5 × 10^−4
(当時、天王星に衛星が 1 つあったと仮定すると);ただし、この共鳴は弱すぎて許可できません
の年齢未満での断熱捕獲と傾斜のために
太陽系。 2 番目に近い強制項には頻度があります
ν3 = s8。 ν3との共鳴を引き起こし、天王星を上に傾ける
大きな傾斜にするには、最小質量の衛星が必要です
m/M = 4.4×10^−4
、つまり、m ≈ 4×10^22 kg (木星よりも小さい)
衛星のエウロパ)。シミュレーションは、天王星がこの共鳴で捕捉されて傾く確率が 100% であることを示しています。
衛星移動率の広い間隔と原始
0◦ の間の傾き εと 20◦傾斜を完了するには
フェーズでは、衛星は約 10 半径の範囲にわたって移動する必要があります。
その歴史の中での天王星。この距離を
太陽系の年齢は、衛星が移動する必要があります
少なくとも6cm/ yr
平均して。この移行率は、過去のモデルから推測できるものよりも桁違いに高い
天王星内の潮汐消散のタイタンで測定された 11 cm/yr (Lainey et al. 2020 を参照)。 Fullerらによって説明されたものと同様のメカニズム。 (2016)は
天王星の周りの急速な衛星拡大の実行可能な説明。
m/M の質量 = 4.4 × 10^−4
天王星の現在の衛星の総質量の約 4 倍です。これは、
関連する衛星はもはや存在せず、存在していたに違いありません
進化の第 2 段階で破壊されました。より大規模な古代の衛星は、他の共鳴に到達することを可能にします。
最も強い共鳴は ν2 = s7 で、衛星の質量 m/M = 2.2 × 10^−3 で到達できます。
.他の有望な共鳴候補は、ν7 = g5 − g7 + s7 および ν5 = −g5 + g6 + s6 であり、到達可能です。
質量 m/M = 1.3 × 10^−3
および 1.7 × 10^−3、それぞれ(つまり木星の衛星カリストとガニメデの質量の間)。
これらの質量推定値は、単一の古代衛星に当てはまります。天王星の場合
当時、追加の内側の衛星系がありました。必要な質量が減少します。たとえば、天王星の現在の衛星と仮想の古代衛星を一緒に配置すると、
システム、上記のすべての質量推定値はで割る必要があります
およそ 2 倍です。
フェーズ 2: 衛星の軌道と
惑星のスピン軸ダイナミクス。システムが
不安定なゾーン、衛星の軌道は非常に急速に興奮する可能性があります
離心率と傾きのほぼすべての値に到達します。もしも
衛星は十分に巨大で、その野生の軌道変動が惑星の自転軸に逆反応を引き起こします: 惑星は掃引します
さまざまな永年スピン軌道共鳴を超えて、不規則な傾斜キックを受けます。これらのキックにより、惑星は大きく動くことができます
不安定な領域でより深くなり、今日の天王星と同様の傾斜角に達します。遅かれ早かれ衛星は
ロシュ限界(または惑星に衝突)、
混沌としたダイナミクスと、最後の惑星の自転を化石化する
州。衛星の衝突は、経年変化の作用によって発生します
赤道傾斜角に位置する共鳴 2ω+ Ω IQ ≈ 56◦
、 と
IQ ≈ 124◦ でその対称対応する 2ω − Ω に
.この共鳴は人工衛星でよく知られています (例えば、Daquin et al.
2022年)。惑星の傾き ε = 90° では消えるので
、 衛生
衝突は、惑星の傾斜角が 90 度よりかなり大きい場合にのみ発生します。
(今日の天王星のように)、またはかなり小さい
90°以上
.興味深いことに、天王星の現在の状態は、
ε > 90◦ におけるヒストグラムの最大値
側。これはあるかもしれません
ここで提案されたメカニズムの支持。
より大きな共鳴とより大規模な衛星が生み出す
より強い斜めキック。私たちのシミュレーションは、m/M = 4.4×10^−4
、衛星は一般的に傾斜が80°に達する前に惑星に衝突します。
.そのため再現は難しいようです
共鳴ν3での捕捉による天王星の現在の状態、
この共鳴が素晴らしい捕獲と傾斜を示したとしても
効率。を生成する可能性のある他の現象について説明しました。
そのような小さな古代の衛星の余分な傾き (例えば、小惑星とのその後の衝突) を見逃していましたが、満足のいくものではありませんでした。
より大規模な衛星は、天王星の現在のスピン状態を再現することにはるかに成功しています。衛星に質量がある場合
m/M 2 ~ 3 × 10^−3、成功の確率 共鳴 ν2 での捕捉は 86% にもなります。わずかに
より小さな質量 (m/M ≈ 1.5 ~ 2 × 10^−3)、共鳴 ν5 と ν7
また、成功率が高く、50% に達するものもあります。
パラメータの範囲。以前のように、天王星がすでに追加のセットを持っていると仮定すると、これらの質量推定値を減らすことができます
当時の内月。しかし、彼らの生存は保証されていません。
共鳴 ν2 は、天王星自身のノードの歳差運動モード s7 との永年スピン軌道共鳴であるため、特別です。そのため
幅が大きいと、衛星を非常に早い段階で不安定にする可能性のある傾斜の大きな振幅の振動が生成されます。
フェーズ 1 の短い通過。さらに、レゾナンス ν2 は非常に強力なキックを生成し、傾斜をすばやく上昇させることができます。
天王星の現在の値に。このため、私たちのシミュレーションは、
衛星が適切な距離で初期化されている限り
(a0 ≈ 50 Req)、共鳴 ν2 を介した傾斜メカニズムは、非常に小さな移動範囲 (代わりに数 Req のみ) まで動作できます。
一般的なケースでは 10 の要件)。の成り立ちを勉強するとき、
Mosqueira & Estrada (2003a,b) は、ガス状の惑星周円盤にある木星、土星、天王星の主要な衛星から、次のことを発見しました。
約 50 Req の距離は、まさに人が期待する場所です。
天王星の周りに形成される巨大な衛星。天王星の現在の主な衛星(ミランダ、アリエル、ウンブリエル、チタニア、オベロン)
巨大惑星の他の衛星と比較して、それらは非常に小さく見えるかもしれません。これらの議論から、少なくとも質量のある衛星を形成すると主張するかもしれません。
比 m/M ≈ 2 × 10^−3
a0 ≈ 50 の距離では Req は見えません
衛星形成理論の文脈ではあまりにも不合理です。
成功した傾斜シナリオは、単に再現するだけではありません。
天王星の現在のスピン状態だけでなく、その存在も可能にします
観測衛星システム。
天王星の今日の主な衛星は、
軌道を順行し、それらは軌道に形成された兆候を示しています
潮汐ディスク (Crida & Charnoz 2012)。可能性について話し合った
天王星の架空の古代衛星の破壊によって生成されたデブリディスクから形成された.
ロシュの制限を下回っています。新世代の形成
衛星は、他の動的プロセスと比較して非常に高速であると予想されます。次に、生まれたばかりの衛星が必要になります
同期軌道から外側に移動する (a ≈ 3.4 Req)
現在の距離まで (Oberon は ≈ 23 Req です)。そのような
従来の潮汐モデルのコンテキストでは、大きな移動範囲は非現実的に見えますが、10億年で達成できる可能性があります
タイタンについて最近提案された「潮汐ロック」と同様のメカニズムが天王星の衛星にも作用している場合のタイムスケール (フラー
ら。 2016;レイニー等。 2020).しかし、これが事実である場合、衛星は、Crida & Charnoz (2012) によって記述された特異な分布に従う特別な理由はありません。
潮汐ディスクの起源。私たちの間の可能な関係
提案された古代の衛星と現在のものは、したがって、
簡単な質問です。
さらに、天王星のスピン状態をうまく再現したシミュレーションのサブセットでは、古代の
衛星が逆行しているときにほとんど常に発生します (IQ ≈ 124◦)。したがって、単純化された長期モデルでは提供されません。
そのから順行潮汐ディスクを生成する簡単な方法
破片、破砕プロセスをモデル化する必要があります
ディスクの特性を評価するための詳細 – 潮汐を含む
衛星内の散逸、軌道および衝突進化
破片の、およびからの追加の噴出物の可能性
星。
これらの問題は、天王星の現在の衛星が原始的であり、同じ気体で形成されていると考えると解決されます
私たちの架空の古代衛星としてのディスク (つまり、Mosqueira & Estrada 2003a,b のシナリオに従う)。明確ではありませんが、
現在の衛星が生き残ったかどうか
それらの大規模な隣人の激しい不安定な段階、およびかどうか
彼らは今日と同じように軌道を非興奮状態に保っていたでしょう。
その後、離心率は潮の散逸によって減衰する可能性があります。
しかし、傾斜は減衰時間スケールがはるかに長くなります。この問題の可能な解決策は、現在の衛星が傾斜中に天王星に近かったことを考慮することです。
その赤道面にしっかりと固定されており、それらが実質的に
その後移住。これらのシナリオには複数の月が含まれるため、
N体シミュレーションを使用してそれらを調査する必要があります
明確な答えを得る。
私たちの結果は、実行された数値探査に基づいています
経年モデルで。の任意の値に対して高速で有効であること
偏心と傾斜、これらのモデルにより、
膨大なパラメータ。進化の第一段階では、
質的に正確な画像を提供することが保証されています。
逆に、第 2 段階では、衛星の離心率が 1 に近づき、歳差が
とても早い。衛星の正確な最終的な運命と潮汐ディスクの特性を決定するには、さらに多くの作業が必要です。
それは作成します。この極端な動的レジームでは、平均化されていない
おそらく数値積分が必要です。
潮汐散逸の影響はまだ調査していません
サテライト内。再び、潮の散逸が影響を与えるだろう
進化の第 2 段階で、衛星の離心率が大幅に増加します。不安定化プロセスの正確な結果を先験的に予測することは困難です。
競合する効果: 惑星内の潮汐散逸 (外向きの衛星移動を生み出す)、動的不安定化
(離心率を増加させる)、および内の潮の散逸
衛星(軌道を円形化し、内側に
移行)。衛星への正味の影響は、以下に大きく依存します。
これら 3 つの競合する効果の相対的なタイムスケール。
でのエネルギー散逸の特定のメカニズムに関連しています。
遊ぶ。巨大氷惑星内部の消散過程は今日では本質的に知られていないため、天王星の内部組成は
古代の衛星は非常に投機的であるため、取得しようとはしませんでした。
ここで明確な答え。ただし、私たちの結果はロバストとして役立ちます
今後の実験の出発点: レベルに応じて
衛星内の潮汐散逸、我々は3つの異なることを期待することができます
挙動: i) 散逸が非常に強い場合、衛星の不安定化は抑制され、我々のシナリオは天王星のスピン状態を再現できません。
ii) 散逸が中程度、不安定化は遅れるかもしれませんが、抑制されません。これにより、1回の実行で成功する割合が増加する可能性があります
小型衛星、質量 m/M ≈ 4.4 × 10^−4 まで
; iii) 散逸が小さい場合、ここで概説した図は変化しません。この記事では、基本的な成分をまとめました。
太古の衛星の移動を介して天王星の現在の状態を再現することができます。このシナリオには洗練のために余地があります
。 1つの有望なバリアントは、2つを呼び出すことです
衛星: 遠くにある大きな衛星 (ここで説明したもの) と小さな衛星
1 つは天王星に非常に近い位置にあります。この構成では、内側の衛星は潮汐移動をはるかに起こしやすくなります。
外側のもの;内側のサテライトが外側に移動する間
数回の Req で、外側の方は効果の変化を感じるでしょう。
天王星の J2 パラメータ。これにより、その特性半径 rM が増加します。その結果、傾斜機構全体は次のようになります。
たとえ遠くの大きな衛星が移行する必要はまったくありません。このバリアント シナリオは、
大きなエネルギーの両方で制約を緩和することが可能です
天王星の内部で必要な散逸(近くの衛星は、より少ないエネルギー散逸を必要とします。遠くのものの移動)、および移動に必要な大きな質量について
古代の衛星(いくつかの適度に組み合わされたアクションとして)大規模な衛星でも同じ効果が得られます)。探検
これと他の可能なバリアント シナリオのうち、将来のために残されます。
動作します。
上記の未回答の質問にもかかわらず、この新しい
天王星の傾斜の写真は、私たちにとって非常に有望に見えます.
私たちの知る限りでは、これは初めての単一のメカニズムです。
天王星を傾ける (フェーズ 1) ことと、その回転軸を化石化することができます。
巨大な衝撃を引き起こすことなく、最終的な状態 (フェーズ 2) で、または
その他の外的現象。成功した実行の大部分はピークに達します
天王星の位置で、これは天王星の自然な結果として現れる
ダイナミクス。この図は、一般的な現象としても魅力的です。今日、木星は傾斜段階を開始しようとしています (Saillenfest et al. 2020)、土星はその中間にある可能性があります (Saillenfest et al.
2021b)、そして天王星は最終段階を完了し、その衛星の破壊.この写真を観察に直面させることは簡単な作業ではありません.
答えの一部は、天王星の現在の衛星の潮汐移動速度の尺度によって与えられます。高い率は、それらが天王星のかなり近くで形成されたことを示します。
それらが古代の衛星の破片から形成された可能性、またはそれらがその野生の不安定化段階から保護された可能性を与えます.




















※コメント投稿者のブログIDはブログ作成者のみに通知されます