
YORP効果で小惑星の赤道にレゴリスが集まり自転速度が上昇して遠心力が引力に勝ると分離してリングになる。リングが離れてロシュ限界を超えるとリング内の物質が集まり衛星になる。以下、機械翻訳。
ディモルフォス形成の再考: ピラミッド体制の視点とディンキネシュの衛星への応用
• Didymos は地滑りを介して物質を軌道上に堆積させます。
• 瞬間的な単一の地滑りは通常、扁長のレモン型のディモルフォスをもたらします。
• 堆積が遅い場合、ディモルフォスは、衝突体とターゲットの質量比が大きい低速衝突によって成長します。
• 堆積が遅い場合、ディモルフォスは非扁長の形状を持つことが予想されます。
• 衝突体と標的の質量比が大きい低速衝突もディンキネシュの衛星形状を説明する可能性がある
概要
ディモルフォスの扁円形は形成モデルに課題をもたらします。 によって誘発されたディディモスの地滑り
YORP 効果により、おそらくディモルフォスが形成されたであろう破片のリングが作成されました。
それにもかかわらず、リング由来の衛星は通常、扁平なレモンの形で形成されます。 を踏まえて、
最新の Dimorphos 形状モデルでは、以前の研究である Madeira らを再検討します。 (2023a)、および
1.0 から 1.5 までの拡張領域で材料堆積を伴う新しい 1D シミュレーションを実施しました。
ディディモス半径。 瞬間的な地滑りにより、長大なディモルフォスが急速に形成される
リングから直接。 さて、ディディモスが徐々に質量を蓄積すると、ディモルフォスは成長します
インパクターとターゲットの質量比が大きい低速衝突 (ピラミッド型の成長)。 平日規模の急速な堆積中に、ディモルフォスはこれらの衝撃のいずれかを経験します。
堆積が遅い場合、衛星の形成は主にピラミッド型の衝突によって行われます。 このプロセスは、
衛星を扁円形 (Leleu et al., 2018) または接触バイナリ形状に再形成します。
調査に値するシナリオであり、より適切なツールを使用して将来的に調査する必要があります。
私たちの結論は、NASA のルーシーによって最近発見されたディンキネシュの衛星にも適用できます。
ミッション。
キーワード:
小惑星、ダイナミクス デブリディスク 惑星環 衛星、形成 衛星、形状
1. はじめに
Didymos の衛星であるDimorphosは、2022年 9月に NASA の DART ミッション探査機によって影響を受けました。
動的偏向技術の初の天文学的スケールのテストのため (Thomas et al., 2023)。 の前に位置します。
ディディモス中心から 𝑎𝑑 = 1183 m での衝突、ディモルフォスの推定質量と密度は 𝑀𝑑 = 4.3 × 10^9 kg 𝜌𝑑 = 2400 kg/m^3
、それぞれ(Naidu et al.、2020; Daly et al.、2022、2023; Thomas et al.、2023)。 明らかになったように
DARTミッションからのデータによると、この物体は著しく扁平な形状をしており、ほぼ軸対称の赤道を持っています。
この領域 (Daly et al., 2023) は、ディモルフォス形成の現在のモデルにとって障害となることが証明されています。 ディディモス
は自転限界近くで回転しており、過去に地滑りや形状変形を経験したと考えられている(Yu et al.,2018年; Zhang et al.、2021; Trogolo et al.、2023)。 これらの出来事により、地球からの破片の輪が発生したと考えられています。
ディモルフォスが形成したと考えられています。 それにもかかわらず、リング降着から直接形成された衛星が期待されています
扁円形とは対照的に、扁平な形状を示す (Porco et al., 2007; Charnoz et al., 2010; Madeira et al., 2023c,a)
ディモルフォスで観察された形状 (Daly et al., 2023)。 ここで、Madeira らの研究を再検討します。 (2023a、以下M23)
そして、1D シミュレーションを通じて、衛星が扁円形 (または
接触バイナリ)形状。 セクション 2 では、M23 の作業と新しい一連の数値シミュレーションについて簡単に説明します。
私たちの結果についてはセクション 3 で取り上げ、結論はセクション 4 で説明します。
2. マデイラらの研究を再訪する。 (2023a)
M23は、ディディモスのスピンアップによる地滑りから生じたディディモスの破片リングからディモルフォスの起源を提案している
YORP 効果によって引き起こされる(Yu et al., 2018; Zhang et al., 2021; Trógolo et al., 2023)。 粘性リングの広がりにより、
ディディモスの流体ロシュ限界 (FRL=1.6926𝑅𝐷) での原始衛星の形成、そして最終的には
ディモルフォスの研究(杉浦ら、2021; 兵藤および杉浦、2022; マデイラら、2023a)。 M23は粘性を重視
1DハイブリッドコードHYDRORINGSを使用したリングの進化とディモルフォの形成(Salmon et al.、2010;Charnoz et al.、2010、2011)。
2 つの異なるシナリオが考慮されます。1 つは、単一の瞬間的なイベントでディディモスの表面に最初の破片のリングが形成されたシナリオで、もう 1 つは、物質が徐々に変化するシナリオです。
物質の堆積関数に従ってディディモスの表面に堆積します。
𝑀̇ (𝑡) =𝑀𝑇/𝜏×exp(−𝑡/𝜏)、(1)
ここでMTはリングに堆積される総質量、𝑡は𝜏形成される最大の衛星の質量は主にMTに依存します
ディディモスの質量の 25% (MD = 5.6 × 10^11 kg、
Daly et al., 2023) の論文が発表されたとき、ディモルフォスの推定質量を備えた衛星を形成するには、円盤に堆積する必要があります。
書かれた。 𝜏 ≤ 1 年間、FRL を超えて広がった物質は凝固してプロトディモルフォスになり、
「継続的体制」(Crida & Charnoz、2012)。 この体制では、新しく形成された衛星は蓄積によって成長します。
リングから直接素材を取り出します。 言い換えれば、リングの端は衛星のヒル球の内側にあるため、どんな物質でも
リングを離れると、近くにある巨大な衛星によって降着されます (詳細については、Crida & Charnoz、2012 を参照。
兵藤ら、2015)。 リングのトルクにより、ディモルフォスは外側に移動し、FRL で形成された小惑星が降着します。
それらは重力の影響範囲内にあります (「離散体制」の成長、Crida & Charnoz、2012)。 このシナリオでは、ディモルフォスは
数十年で最終質量に達し、扁長凝集体になると予想される (Porco et al., 2007; Charnoz et al.,2010)。
𝜏 ≧10^2 年以上の場合、状況は異なります。衛星は、10^2 年の間、ディモルフォスの質量の数パーセントにしか到達しません。
継続的な体制。 衛星が遠ざかるにつれて、システムは同様のサイズの衛星の集合に進化します。
最終的に衝突してディモルフォスを形成します。 この成長体制は「ピラミッド体制」として定義されます(Crida & Charnoz、
2012)、ディモルフォスが形成されるまでには数千年かかります。 レルーら。 (2018) は、低速の影響があることを示しています。
ピラミッド型の状態では、土星で観察されたものと同様に、扁円形の天体が形成される可能性があります。
これは扁平ディモルフォスにも関連する可能性があります (Daly et al., 2023)。
ただし、ピラミッド型体制におけるディモルフォの形成が遅いことに関しては、いくつかの注意点があります。 数値
シミュレーションによると、地滑りは通常数時間しか続かないことが示されています (Sagiura et al., 2021; Hyodo & Sugaura, 2022)。
私たちのものよりもかなり短いタイムスケールです。 さらに、ディディモスは太陽の影響を強く受けるため、
物体の周囲の材料の寿命 (Rossi et al., 2022; Madeira et al., 2023b を参照)。 したがって、より迅速な形成
ディモルフォスがおすすめです。
ここでは、ディモルフォスのピラミッド型体制の成長をより正確に調査するための新しいシミュレーションを紹介します。 私たちの数値
モデルは永年摂動理論を使用して改良され、一次衛星相互作用を計算しました (Brouwer &クレマンス、1961年。 ダーモットとニコルソン、1986)。 永年相互作用は軌道要素の振動を誘発し、
シミュレーションの各ステップで、衛星の妨害関数の永年項を導き出し、それを解いて、
強制要素 (詳細については、Murray & Dermott、1999 年の第 7 章を参照)。 さらに、偏心率を計算します。
一次平均運動共鳴の交差により衛星を蹴る (Murray & Dermott、1999; Madeira & ジュリアッティ冬、2020)。
これにより、衛星の離心率を (少なくとも大きさのオーダーで) 計算できます。
これにより、衝突速度を大まかに推定できるようになります。
シミュレーションを高速化するために、限られた領域ではなく、より広い領域を占めるデブリ リングから開始します。
プライマリーの表面に。 確かに兵藤・杉浦 (2022); トローゴロら。 (2023) は材料が
M23で想定されていたものよりもはるかに広い領域にわたって放出され、その結果に基づいて、我々は一様な分布を想定している。
Didymos の表面 (𝑅𝐷 = 382 m、Daly et al.、2023) から 1.5𝑅𝐷 までの物質の堆積。 Didymos の潮汐パラメータは
𝑘2∕𝑄 = 10^−5 として設定します。
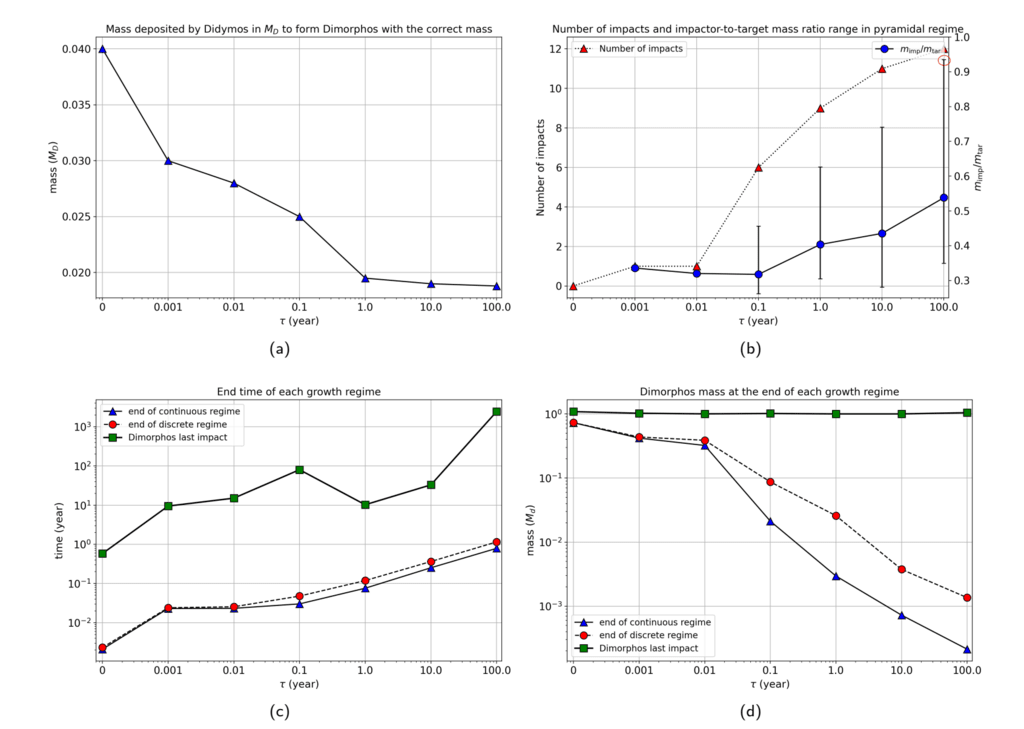
図 1: 堆積時間スケールの関数としてのディモルフォ形成の概要 𝜏 を示すパネル: a) 総質量𝑀𝑇
ディモルフォ編成用。 b) ピラミッド型体制における衝突の数 (左の Y スケール、破線) と平均
インパクターとターゲットの質量比 mimp/mtar (右の y スケール、実線)。エラーバーは mimp/mtar の範囲を示します。 c) 時間
d) 連続体制、離散体制、およびディモルフォスとの最後の衝突の終わりにおけるディモルフォスの質量。
3. 拡張デブリリングシミュレーションとディモルフォ形成
まず、瞬間的に形成されたリングの場合 (𝜏 = 0) を検討し、次に Didymos が発生するシナリオを検討します。
堆積時間スケールにわたって段階的にリングを供給します 𝜏^1(𝜏 = 10^−3− 10^2 年)。 私たちのシミュレーションを要約すると、
瞬間的な堆積の場合、ディモルフォはわずか 0.04 MD のリングから形成できます (図 1a)。
狭く閉じ込められたリングを想定した M23 で報告された値よりもはるかに低い値です。 この矛盾は主に、
どちらの場合もリングの角運動量が同等であるためです。 M23 の場合、全角運動量は
系への角運動量は ~ 2 × 10^−12 𝑚^2∕𝑠 ですが、瞬間的に形成された拡張リングの角運動量は次のようになります。
3 × 10^−12 𝑚^2∕𝑠.瞬間的な場合、プロトディモルフォスは約 0.74 Md に達します。
連続21時間(~0.04年)で離散レジーム(図1c、1d)。 衛星は、リング トルクにより到達可能な最も遠い距離であるロシュ限界 (a ~ 1027 m) の 2:1 MMR 位置に到達するまで外側に移動します。 この場所で、ディモルフォスはその目的を達成します。
最終質量 Md
インパクターとターゲットの質量比が mimp/mtar ~ 5 ~ 15% の 3 回の衝突で、~ 6 か月以内。 これ
ここの衝突体は原ディモルフォスよりもはるかに小さいため、典型的なピラミッド型の体制とは異なります。 を考慮して
これにより、ピラミッド型レジームで考慮される影響の限界値 mimp/mtar=0.25 を定義します。 インパクトが満たされない
この条件は 𝜏 = 0 年であり、したがって、扁長ディモルフォスが形成されると予想されます。
次に、Didymos が徐々にリングを供給するシナリオを検討してみましょう。 𝜏ディモルフォスの形成が減少します。 𝜏
ディディモスに落下し、リング質量を衛星に変換する効率が向上します。 ただし、これも結果として、
ロシュ限界でのより小さな衛星の形成において。 その結果、𝜏
連続的および離散的領域では成長が見られますが、ピラミッド型ではインパクトの数が増加しています。
政権。
𝜏 = 0.001 年と 0.01 年の場合、ディモルフォスは連続領域と離散領域で約 0.4Md の質量を獲得します。
その後、ピラミッド型政権の影響は 1 つだけ発生しました。 ただし、これにより形が変わる可能性があります。 𝜏
ほとんどの場合、ピラミッド状領域で形成され、より高い質量比でより多くの衝突が得られます。 これらの衝突は次の場所で発生します。
相互逃走速度が ~ 2 ~ 3 であり、部分的な降着や当て逃げを引き起こす可能性があり、潜在的に危険を引き起こす可能性があります。
非扁平衛星に(Leleu et al., 2018)。 これは、𝜏 = 100 年で特に顕著であり、最大 mimp/mtar = 0.94 (赤丸) であるため、接触連星形状の衛星が発生する可能性があります。 このような速度で同様のサイズの物体が関与する衝突は、Leleu らの場合に似ています。 (2018) 扁円形が得られます。
4. 結論
マデイラらを再訪します。 (2023a) 拡張ディスクとより短い質量堆積による新しいシミュレーションを実施
ディディモスのタイムスケール。 ディディモスで瞬間的な地滑りが起こり、その質量の 4% が均一に分布し、
おそらく扁長の形状ではあるものの、わずか数時間でディモルフォスが形成されます。 しかし、有限の堆積事象を仮定すると、
持続期間中、リングから直接ディモルフォスの成長は抑制され、衛星は低速、高質量比の衝突を通じて質量を蓄積します。 数日間続く堆積の中でも、ディモルフォスはそのような衝撃を受けます。
潜在的にその初期の扁平形状を変える可能性があります。 より長い期間のイベントはピラミッドのほぼ完全な成長につながります
(Crida & Charnoz、2012)。 この体制に関連する衝撃により、観察されたように扁平な物体が生じる可能性があります。
DARTミッションによる。 これらの結論は、最近発見された小惑星 (152830) の衛星にも確かに当てはまります。
ルーシーミッションによるディンキネシュ。 この衛星は接触連星であり、2 つの衛星間の低速遭遇の結果です。
等しいサイズの衛星、これがピラミッド型の体制を定義します。
ディモルフォス形成の再考: ピラミッド体制の視点とディンキネシュの衛星への応用
• Didymos は地滑りを介して物質を軌道上に堆積させます。
• 瞬間的な単一の地滑りは通常、扁長のレモン型のディモルフォスをもたらします。
• 堆積が遅い場合、ディモルフォスは、衝突体とターゲットの質量比が大きい低速衝突によって成長します。
• 堆積が遅い場合、ディモルフォスは非扁長の形状を持つことが予想されます。
• 衝突体と標的の質量比が大きい低速衝突もディンキネシュの衛星形状を説明する可能性がある
概要
ディモルフォスの扁円形は形成モデルに課題をもたらします。 によって誘発されたディディモスの地滑り
YORP 効果により、おそらくディモルフォスが形成されたであろう破片のリングが作成されました。
それにもかかわらず、リング由来の衛星は通常、扁平なレモンの形で形成されます。 を踏まえて、
最新の Dimorphos 形状モデルでは、以前の研究である Madeira らを再検討します。 (2023a)、および
1.0 から 1.5 までの拡張領域で材料堆積を伴う新しい 1D シミュレーションを実施しました。
ディディモス半径。 瞬間的な地滑りにより、長大なディモルフォスが急速に形成される
リングから直接。 さて、ディディモスが徐々に質量を蓄積すると、ディモルフォスは成長します
インパクターとターゲットの質量比が大きい低速衝突 (ピラミッド型の成長)。 平日規模の急速な堆積中に、ディモルフォスはこれらの衝撃のいずれかを経験します。
堆積が遅い場合、衛星の形成は主にピラミッド型の衝突によって行われます。 このプロセスは、
衛星を扁円形 (Leleu et al., 2018) または接触バイナリ形状に再形成します。
調査に値するシナリオであり、より適切なツールを使用して将来的に調査する必要があります。
私たちの結論は、NASA のルーシーによって最近発見されたディンキネシュの衛星にも適用できます。
ミッション。
キーワード:
小惑星、ダイナミクス デブリディスク 惑星環 衛星、形成 衛星、形状
1. はじめに
Didymos の衛星であるDimorphosは、2022年 9月に NASA の DART ミッション探査機によって影響を受けました。
動的偏向技術の初の天文学的スケールのテストのため (Thomas et al., 2023)。 の前に位置します。
ディディモス中心から 𝑎𝑑 = 1183 m での衝突、ディモルフォスの推定質量と密度は 𝑀𝑑 = 4.3 × 10^9 kg 𝜌𝑑 = 2400 kg/m^3
、それぞれ(Naidu et al.、2020; Daly et al.、2022、2023; Thomas et al.、2023)。 明らかになったように
DARTミッションからのデータによると、この物体は著しく扁平な形状をしており、ほぼ軸対称の赤道を持っています。
この領域 (Daly et al., 2023) は、ディモルフォス形成の現在のモデルにとって障害となることが証明されています。 ディディモス
は自転限界近くで回転しており、過去に地滑りや形状変形を経験したと考えられている(Yu et al.,2018年; Zhang et al.、2021; Trogolo et al.、2023)。 これらの出来事により、地球からの破片の輪が発生したと考えられています。
ディモルフォスが形成したと考えられています。 それにもかかわらず、リング降着から直接形成された衛星が期待されています
扁円形とは対照的に、扁平な形状を示す (Porco et al., 2007; Charnoz et al., 2010; Madeira et al., 2023c,a)
ディモルフォスで観察された形状 (Daly et al., 2023)。 ここで、Madeira らの研究を再検討します。 (2023a、以下M23)
そして、1D シミュレーションを通じて、衛星が扁円形 (または
接触バイナリ)形状。 セクション 2 では、M23 の作業と新しい一連の数値シミュレーションについて簡単に説明します。
私たちの結果についてはセクション 3 で取り上げ、結論はセクション 4 で説明します。
2. マデイラらの研究を再訪する。 (2023a)
M23は、ディディモスのスピンアップによる地滑りから生じたディディモスの破片リングからディモルフォスの起源を提案している
YORP 効果によって引き起こされる(Yu et al., 2018; Zhang et al., 2021; Trógolo et al., 2023)。 粘性リングの広がりにより、
ディディモスの流体ロシュ限界 (FRL=1.6926𝑅𝐷) での原始衛星の形成、そして最終的には
ディモルフォスの研究(杉浦ら、2021; 兵藤および杉浦、2022; マデイラら、2023a)。 M23は粘性を重視
1DハイブリッドコードHYDRORINGSを使用したリングの進化とディモルフォの形成(Salmon et al.、2010;Charnoz et al.、2010、2011)。
2 つの異なるシナリオが考慮されます。1 つは、単一の瞬間的なイベントでディディモスの表面に最初の破片のリングが形成されたシナリオで、もう 1 つは、物質が徐々に変化するシナリオです。
物質の堆積関数に従ってディディモスの表面に堆積します。
𝑀̇ (𝑡) =𝑀𝑇/𝜏×exp(−𝑡/𝜏)、(1)
ここでMTはリングに堆積される総質量、𝑡は𝜏形成される最大の衛星の質量は主にMTに依存します
ディディモスの質量の 25% (MD = 5.6 × 10^11 kg、
Daly et al., 2023) の論文が発表されたとき、ディモルフォスの推定質量を備えた衛星を形成するには、円盤に堆積する必要があります。
書かれた。 𝜏 ≤ 1 年間、FRL を超えて広がった物質は凝固してプロトディモルフォスになり、
「継続的体制」(Crida & Charnoz、2012)。 この体制では、新しく形成された衛星は蓄積によって成長します。
リングから直接素材を取り出します。 言い換えれば、リングの端は衛星のヒル球の内側にあるため、どんな物質でも
リングを離れると、近くにある巨大な衛星によって降着されます (詳細については、Crida & Charnoz、2012 を参照。
兵藤ら、2015)。 リングのトルクにより、ディモルフォスは外側に移動し、FRL で形成された小惑星が降着します。
それらは重力の影響範囲内にあります (「離散体制」の成長、Crida & Charnoz、2012)。 このシナリオでは、ディモルフォスは
数十年で最終質量に達し、扁長凝集体になると予想される (Porco et al., 2007; Charnoz et al.,2010)。
𝜏 ≧10^2 年以上の場合、状況は異なります。衛星は、10^2 年の間、ディモルフォスの質量の数パーセントにしか到達しません。
継続的な体制。 衛星が遠ざかるにつれて、システムは同様のサイズの衛星の集合に進化します。
最終的に衝突してディモルフォスを形成します。 この成長体制は「ピラミッド体制」として定義されます(Crida & Charnoz、
2012)、ディモルフォスが形成されるまでには数千年かかります。 レルーら。 (2018) は、低速の影響があることを示しています。
ピラミッド型の状態では、土星で観察されたものと同様に、扁円形の天体が形成される可能性があります。
これは扁平ディモルフォスにも関連する可能性があります (Daly et al., 2023)。
ただし、ピラミッド型体制におけるディモルフォの形成が遅いことに関しては、いくつかの注意点があります。 数値
シミュレーションによると、地滑りは通常数時間しか続かないことが示されています (Sagiura et al., 2021; Hyodo & Sugaura, 2022)。
私たちのものよりもかなり短いタイムスケールです。 さらに、ディディモスは太陽の影響を強く受けるため、
物体の周囲の材料の寿命 (Rossi et al., 2022; Madeira et al., 2023b を参照)。 したがって、より迅速な形成
ディモルフォスがおすすめです。
ここでは、ディモルフォスのピラミッド型体制の成長をより正確に調査するための新しいシミュレーションを紹介します。 私たちの数値
モデルは永年摂動理論を使用して改良され、一次衛星相互作用を計算しました (Brouwer &クレマンス、1961年。 ダーモットとニコルソン、1986)。 永年相互作用は軌道要素の振動を誘発し、
シミュレーションの各ステップで、衛星の妨害関数の永年項を導き出し、それを解いて、
強制要素 (詳細については、Murray & Dermott、1999 年の第 7 章を参照)。 さらに、偏心率を計算します。
一次平均運動共鳴の交差により衛星を蹴る (Murray & Dermott、1999; Madeira & ジュリアッティ冬、2020)。
これにより、衛星の離心率を (少なくとも大きさのオーダーで) 計算できます。
これにより、衝突速度を大まかに推定できるようになります。
シミュレーションを高速化するために、限られた領域ではなく、より広い領域を占めるデブリ リングから開始します。
プライマリーの表面に。 確かに兵藤・杉浦 (2022); トローゴロら。 (2023) は材料が
M23で想定されていたものよりもはるかに広い領域にわたって放出され、その結果に基づいて、我々は一様な分布を想定している。
Didymos の表面 (𝑅𝐷 = 382 m、Daly et al.、2023) から 1.5𝑅𝐷 までの物質の堆積。 Didymos の潮汐パラメータは
𝑘2∕𝑄 = 10^−5 として設定します。

図 1: 堆積時間スケールの関数としてのディモルフォ形成の概要 𝜏 を示すパネル: a) 総質量𝑀𝑇
ディモルフォ編成用。 b) ピラミッド型体制における衝突の数 (左の Y スケール、破線) と平均
インパクターとターゲットの質量比 mimp/mtar (右の y スケール、実線)。エラーバーは mimp/mtar の範囲を示します。 c) 時間
d) 連続体制、離散体制、およびディモルフォスとの最後の衝突の終わりにおけるディモルフォスの質量。
3. 拡張デブリリングシミュレーションとディモルフォ形成
まず、瞬間的に形成されたリングの場合 (𝜏 = 0) を検討し、次に Didymos が発生するシナリオを検討します。
堆積時間スケールにわたって段階的にリングを供給します 𝜏^1(𝜏 = 10^−3− 10^2 年)。 私たちのシミュレーションを要約すると、
瞬間的な堆積の場合、ディモルフォはわずか 0.04 MD のリングから形成できます (図 1a)。
狭く閉じ込められたリングを想定した M23 で報告された値よりもはるかに低い値です。 この矛盾は主に、
どちらの場合もリングの角運動量が同等であるためです。 M23 の場合、全角運動量は
系への角運動量は ~ 2 × 10^−12 𝑚^2∕𝑠 ですが、瞬間的に形成された拡張リングの角運動量は次のようになります。
3 × 10^−12 𝑚^2∕𝑠.瞬間的な場合、プロトディモルフォスは約 0.74 Md に達します。
連続21時間(~0.04年)で離散レジーム(図1c、1d)。 衛星は、リング トルクにより到達可能な最も遠い距離であるロシュ限界 (a ~ 1027 m) の 2:1 MMR 位置に到達するまで外側に移動します。 この場所で、ディモルフォスはその目的を達成します。
最終質量 Md
インパクターとターゲットの質量比が mimp/mtar ~ 5 ~ 15% の 3 回の衝突で、~ 6 か月以内。 これ
ここの衝突体は原ディモルフォスよりもはるかに小さいため、典型的なピラミッド型の体制とは異なります。 を考慮して
これにより、ピラミッド型レジームで考慮される影響の限界値 mimp/mtar=0.25 を定義します。 インパクトが満たされない
この条件は 𝜏 = 0 年であり、したがって、扁長ディモルフォスが形成されると予想されます。
次に、Didymos が徐々にリングを供給するシナリオを検討してみましょう。 𝜏ディモルフォスの形成が減少します。 𝜏
ディディモスに落下し、リング質量を衛星に変換する効率が向上します。 ただし、これも結果として、
ロシュ限界でのより小さな衛星の形成において。 その結果、𝜏
連続的および離散的領域では成長が見られますが、ピラミッド型ではインパクトの数が増加しています。
政権。
𝜏 = 0.001 年と 0.01 年の場合、ディモルフォスは連続領域と離散領域で約 0.4Md の質量を獲得します。
その後、ピラミッド型政権の影響は 1 つだけ発生しました。 ただし、これにより形が変わる可能性があります。 𝜏
ほとんどの場合、ピラミッド状領域で形成され、より高い質量比でより多くの衝突が得られます。 これらの衝突は次の場所で発生します。
相互逃走速度が ~ 2 ~ 3 であり、部分的な降着や当て逃げを引き起こす可能性があり、潜在的に危険を引き起こす可能性があります。
非扁平衛星に(Leleu et al., 2018)。 これは、𝜏 = 100 年で特に顕著であり、最大 mimp/mtar = 0.94 (赤丸) であるため、接触連星形状の衛星が発生する可能性があります。 このような速度で同様のサイズの物体が関与する衝突は、Leleu らの場合に似ています。 (2018) 扁円形が得られます。
4. 結論
マデイラらを再訪します。 (2023a) 拡張ディスクとより短い質量堆積による新しいシミュレーションを実施
ディディモスのタイムスケール。 ディディモスで瞬間的な地滑りが起こり、その質量の 4% が均一に分布し、
おそらく扁長の形状ではあるものの、わずか数時間でディモルフォスが形成されます。 しかし、有限の堆積事象を仮定すると、
持続期間中、リングから直接ディモルフォスの成長は抑制され、衛星は低速、高質量比の衝突を通じて質量を蓄積します。 数日間続く堆積の中でも、ディモルフォスはそのような衝撃を受けます。
潜在的にその初期の扁平形状を変える可能性があります。 より長い期間のイベントはピラミッドのほぼ完全な成長につながります
(Crida & Charnoz、2012)。 この体制に関連する衝撃により、観察されたように扁平な物体が生じる可能性があります。
DARTミッションによる。 これらの結論は、最近発見された小惑星 (152830) の衛星にも確かに当てはまります。
ルーシーミッションによるディンキネシュ。 この衛星は接触連星であり、2 つの衛星間の低速遭遇の結果です。
等しいサイズの衛星、これがピラミッド型の体制を定義します。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます