
「解の公式」と呼ばれるものには色々ありますが,その中でも多くの方にとって最初に(そしてひょっとすると最後に?)出逢うのが【2次方程式の解の公式】なのではないかと思います.
一般に x の2次方程式は,定数 a (≠ 0), b, c を用いて次のように表すことができます:
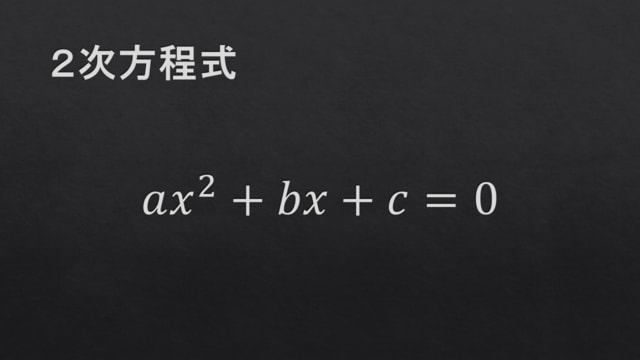
このような方程式を解きたいとき,解の公式はとても頼りになります(☞注1):

色々な方法で証明することができますが,今回は【平方完成】によって導いてみました:
最初に 4a を掛け算しているのは,後の式変形で a^2 の根号(ルート)を外すというステップが現れるのをあらかじめ防ぐためです.つまり厄介な議論を回避するのが主な目的です(☞注2).
1分間で間に合ったようです.
3次や4次の方程式の解の公式を果たして1分間で証明することは可能なのでしょうか...? 僕では公式を書くだけでも1分で足りないような気がします(笑)
注1.「方程式を解く」というのは要するに,「このような関係を満たす未知数 x は何でしょう?」というなぞなぞに答えることです.
注2.このトリックは,昔どこかで聞いて知ったものだったような気もしますが,よく思い出せません.高校生になって実定数の2次方程式について解の公式を導こうとしたとき,場合分けが要ることに気づきました.中学生のときの自分が納得していた導出には穴があったのだと知って愕然としました.また複素定数だと一体どうしたらよいのだろうと震えたことを覚えています(笑)
もし文献をご存知の方がいらっしゃいましたら,教えていただけると嬉しいです.
















※コメント投稿者のブログIDはブログ作成者のみに通知されます