【１分レシピ】 タンジェントの加法定理

　先の記事において【タンジェント（tan）の加法定理】を用いましたので，あわせて証明を紹介します．

 

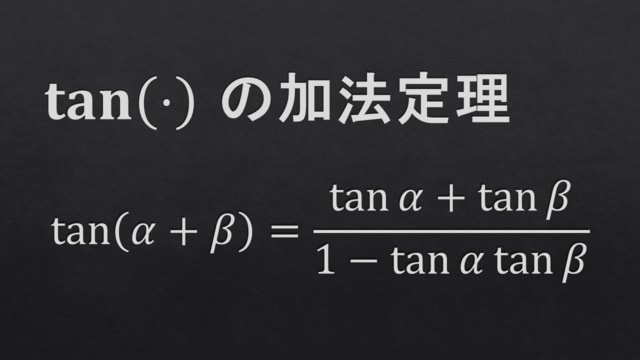
　今回は，サイン（sin）およびコサイン（cos）の加法定理は既に知っているものとします（※こちらも面白いので別の記事にて改めて証明やその周辺を紹介したい所存です）．

 

　次のようにして，素朴に導くことができます：

 

【余談】

　三角関数には複数の定義の仕方があり，それぞれで定義域が異なります．しかし，sin(・) と cos(・) の加法定理を前提として用いれば，特に定義域を気にすることなく tan(・) の加法定理を導出できます．その点で上記の証明の方針は優れているように思います．

　一方，定義域を制限して (0, π/2) とすれば（i.e. 直角三角形を用いた定義），幾何的でもっと直感に訴えかけるような証明ができそうな気がします🤔

　もし面白い証明方法をご存知の方がいらっしゃいましたら，ご教示いただけると嬉しいです．

 

数学ランキング