先の記事において【タンジェント（tan）の加法定理】を用いましたので，あわせて証明を紹介します．
今回は，サイン（sin）およびコサイン（cos）の加法定理は既に知っているものとします（※こちらも面白いので別の記事にて改めて証明やその周辺を紹介したい所存です）．
次のようにして，素朴に導くことができます：
【余談】
三角関数には複数の定義の仕方があり，それぞれで定義域が異なります．しかし，sin(・) と cos(・) の加法定理を前提として用いれば，特に定義域を気にすることなく tan(・) の加法定理を導出できます．その点で上記の証明の方針は優れているように思います．
一方，定義域を制限して (0, π/2) とすれば（i.e. 直角三角形を用いた定義），幾何的でもっと直感に訴えかけるような証明ができそうな気がします🤔
もし面白い証明方法をご存知の方がいらっしゃいましたら，ご教示いただけると嬉しいです．
本日の数理パズルは，京都大学の入試問題から．
稀に見る問題文の短さから，受験業界では非常に有名な過去問なのだそうです．
【問題】 tan(1°) は有理数か？
シンプルですが面白い問題ですよね．僕の解答案は次の通りです：
※今のところ，この動画のシリーズを視聴してくださる方のおよそ半数が英語話者なので，スライドのみ英語にて作成してみています．字幕（日本語・英語）を利用できます．動画内で用いた記法やロジックについて，必要あれば注1，2を参照ください．
動画内では，【タンジェントの加法定理】を用いて，【背理法】によって示しました．
タンジェントの加法定理は，次式で表されます：
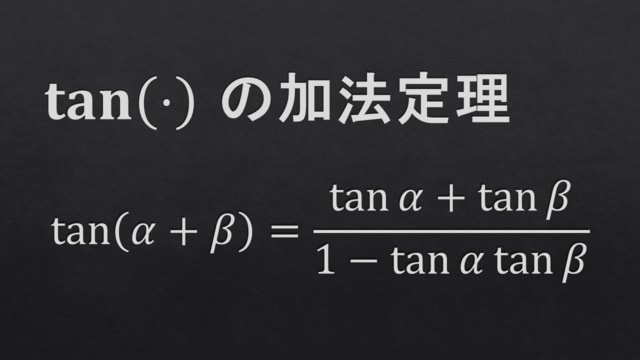
※先日証明したので，別の記事にて簡単に紹介したい所存です．
また類題として「cos(1°)，sin(1°) は有理数か？」が素朴に思いつきます．
cos と sin，tan の間には
sin(1°) = tan(1°) cos(1°)
という関係があるので，cos(1°) または sin(1°) のいずれかが無理数であることを示せれば，（背理法によって）他方も無理数であることがただちに示せます．またsec(1°), csc(1°), cot(1°) が無理数であることもただちに従います．
みなさんは cos(1°)，sin(1°)，tan(1°) の無理数性をどのように証明されますか？
注1．動画内で用いた記法について
(1) 有理数全体の集合をQという記号で表しています．
(2) 「a ∈ S」というのは「要素 a は集合 S に属す」ことを表す記法です．
たとえば「tan(1°) ∈ Qと仮定する」と書かれていれば，「tan(1°) は有理数であると仮定する」という意味です．
(3) 「a ∉ S」というのは「要素 a は集合 S に属さない」ことを表す記法です．
たとえば「tan(1°) ∉ Q」と書かれていれば「tan(1°) は有理数でない」，つまり「tan(1°) は無理数である」という意味です．
注2．証明のロジックについて
(4) 【有理数】とは，a, b という2つの整数（..., -2, -1, 0, 1, 2, ...という数）を使って比 a/b で表すことができる数のことです（ただし b ≠ 0 とする）．
(5) 2つの有理数 r と s について，和 r + s，差 r - s，積 rs，商 r/s（ただし s ≠ 0）のいずれもまた有理数となります．
(6) 「tan(1°) が有理数である」と仮定するとき，tan(1°) + tan(1°) は有理数どうしの和なので有理数です．
また 1 - tan(1°)tan(1°) は有理数から有理数どうしの積を引いたものなので，やはり有理数ということになります．
(7) 【タンジェントの加法定理】より，tan(2°) というのは tan(1°) + tan(1°) を 1 - tan(1°)tan(1°) で割ったものです．つまり，仮定の下では有理数どうしの商で表されるので，「tan(2°) もまた有理数」ということになります．3°以降についても同様の議論を繰り返します．
【出典】
京都大学．(2006)．後期入試試験，第6問．
一部の界隈で話題になっているTシャツを，少し前にネットショップで購入しました．
衝動的に黒と紺の2色も買ってしまったのですが，デザインがとても気に入っています：
しかし，届いたものを手に取って眺めてみると2つほど【違和感】に気づきました．．．
みなさんもお気づきになられたでしょうか？
そうです．y = sin(x) のグラフの位相が π だけずれているのです😨
そして y = log_a(x) のグラフに至っては，なぜか逆関数（y = a^x : 0 < a < 1）を示しています．
買うときには気づかなかったなあ（笑）
でも，それも含めて数学好きの方との話の種になるので良いかな，と思っています．
いわゆるマスメディアを全く観ないこともあって世情に疎く，幼いときから流行りには感冒くらいしか付いていけたことがありません．
ですから，同年代の方々が流行り言葉を使っていても，頭にクエスチョンマーク（？）が浮かぶことがしばしばです．
近年，「神〇〇」や「まじで神！」などという言い回しをよく耳にしますが，とにかく違和感がすごいです（笑） ずいぶん安い「神」だなあ．．．
この手の言葉ではじめて耳にしたのは【神対応】でした．思いがけない語彙の組合せだったので，度肝を抜かれました．
脳裏に過ぎったのは数学の集合論でいうところの「対応」．僕のなかではこんなイメージです（笑）：
定義 「f が神対応である」
※どうしようもないダジャレによるお目汚し，たいへん失礼したしました．
よい一日を．
おはようございます！本日もパズルを紹介します．
【問題】 次の平行四辺形の面積はいくつでしょうか？
この問題も以前，塾でアルバイトしていたとき生徒さんに QUIZ（小テスト）として出題していたものです．
たとえば，次のような等積変形を考えることで算出できます：
※今のところ，この動画のシリーズを視聴してくださる方のおよそ半数が英語話者なので，スライドのみ英語にて作成してみています．字幕（日本語・英語）を利用できます．
もともとは高校生のとき，2次の行列式の幾何的な意味を考えている中で思いついた解法です．画期的なアイディアだとは思いませんが，一つの素朴なイメージとして個人的には気に入っています．
3次の行列式も同様に6つの直方体の体積を足し引きすることによって，（3本のベクトルによって空間上に張られる）平行六面体の符号付き体積を表すと解釈できたはずです．
”はず” というのは，項が多いため久々にやろうとするのが億劫で躊躇っているからです（笑）今晩，寝床のなかで考えてみたいと思います．
3次の場合の幾何的な導出に成功された方がいらっしゃいましたら，ぜひコメントにてご教示のほどお願いします！
【蛇足】 ボツにした追加問題
4次元のユークリッド空間において，2つの線型独立なベクトル (x_1, y_1, z_1, w_1) および (x_2, y_2, z_2, w_2) が張る平行四辺形の面積はどのように表されるでしょうか？
※ 2次元のユークリッド空間の場合，2つの線型独立なベクトル (x_1, y_1) および (x_2, y_2) が張る平行四辺形の面積 S は，上で紹介したように S = |x_1 * y_2 – x_2 * y_1| と表すことができます．
