学校は4月が新学期スタートですが、
塾ではもう2月から新学年ですね。
4年生だけど、5年生のこと。
スタートで躓きたくない。
はやく新しい塾に慣れなくては。
初めのテストでよい点を取ってよい滑り出しにしたい。
そんな想いを持ちながら新しい学年を迎えている生徒さんも多いの
確かにそうです。
初めが肝心
今日は、
についてお話ししたいと思います。
①計算力
どんな問題でも最低限の計算力は必要になります。
以下に示す数値は、
まずは、暗記しておいてほしい数値、それは、分数から小数、
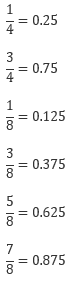
また、円周率3.14の計算も一桁倍は覚えておきましょう。
3.14×1=3.14
3.14×2=6.28
3.14×3=9.42
3.14×4=12.56
3.14×5=15.70
(
3.14×6=18.84
3.14×7=21.98
3.14×8=25.12
3.14×9=28.26
なぜ覚えなくてはいけないのか。
それは、
見たことある数値だな。あれ?見たことない数がでたぞ。
と、テストを受けているときに、自問自答しながら解いていくと、
自分で計算ミスに気付けるようになってきます。
②文章をよく読む
この言葉は、1月の受験直前期、
解くことに夢中になってしまうと、どうしても「読みミス」「
をしてしまいます。
とにかく、
では、どういうところで間違えてしまうのか。
例えば、
(1)101を割ると5余り、
という問題と、
(2)7で割ると5余り、
という2つの問題があるとします。
この問題でよくあるミスが、「を」と「で」の読み間違いです。
割る数を出すのか、割られる数を求めるのかが違うのです。
(1)101を割ると5余り、135を割ると3余る数の中で最も
(2)7で割ると5余り、5で割ると3余る整数の中で一番小さい
似ている問題ですが、「を」と「で」
(1)を式に表してみると、
101÷□=△…5
135÷□=〇…3
(2)を式に表してみると、
□÷7=☆…5
□÷3=◆…3
(1)と(2)で違うのは、□の位置です。
A÷Bを日本語にしてみると「AをBで割る」と言いますよね。
つまり、「~を」の~には、A=割られる数、「~で」の~には、
「を」と「で」で全く違うんですよね。
この「を」と「で」の違いは、
算数的には、倍数を求めるのか、
A=割られる数を求めるときは、倍数です。
B=割る数を求めるときは、約数になります。
では、(1)を解いていきましょう。
101÷□=△…5
135÷□=〇…3
101-5=96
135-3=132
この2つの数はともに割り切れる数になるので、96と132の公
右図の連除法で解くと、

つまり、2×2×3=12←最大公約数
12の約数=〔1,2,3,4,6,12〕
で、余りの5と3より大きい数字でなくてはいけないので、
その中で一番小さい数は6
次に(2)は、
□÷7=☆…5
□÷5=◆…3
□が割るの前にあります。
つまり、□は割られる数なので、倍数を求めることになります。
また、この問題はもう一つ解くポイントがあります。
それは、7-5=2、5-3=2となり、割る数―
そこに注目し、まずは、7と5の最小公倍数=35を求め、
35-2=33
この「を」と「で」
③「もし」「~すると」の言葉に注意
問題:AはBの5倍のお金を持っています。もし、
という問題があるとします。
結局聞かれていることは、Aが持っているお金、つまり、
「もし、~~あげると」とあるように、まだあげていません。
まだ推定です。あげるとそうなるけど、
現在の所持金を答えなくてはいけません。
大したことない問題かもしれませんが、
では、解いていきましょう。
AとBの和は、
比を求めて、和に注目します。
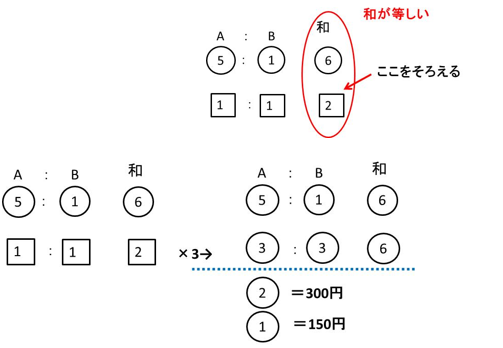
①=150円なので、Aの所持金は、⑤=150×5=750円
大丈夫だとは思うのですが、
問題を解いているときは、
簡単なところでまちがってしまうということがあります。
言葉は大事ですね。
ちょっとした部分もしっかりと読み取って、
心がけていきましょう。
授業では、そういった細かいミスを見逃さないよう、
つっこみを入れていきます。
「文章を読む」「問題文をしっかりと読む」
算数の勉強の躓きを一緒になくしていきましょう!















