線分図 中学算数 後半

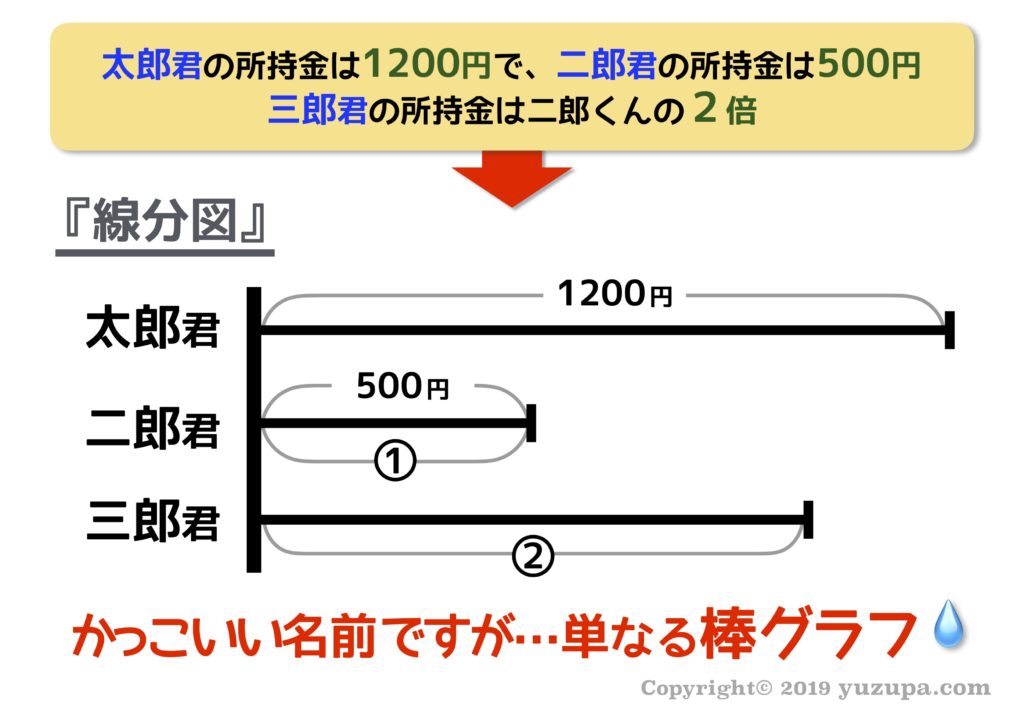
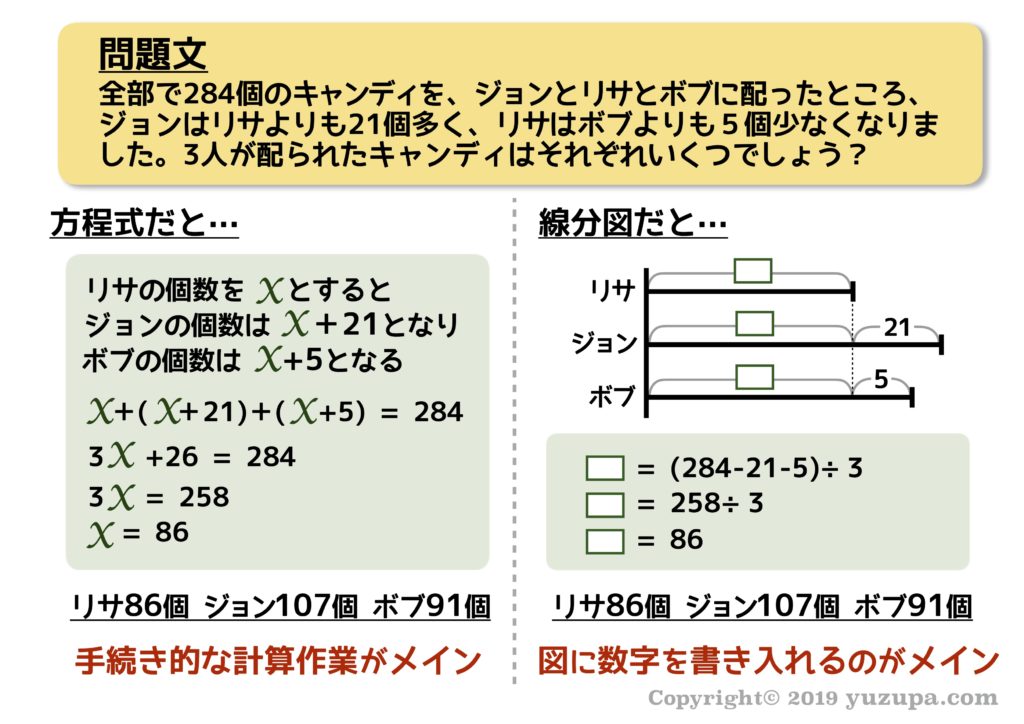
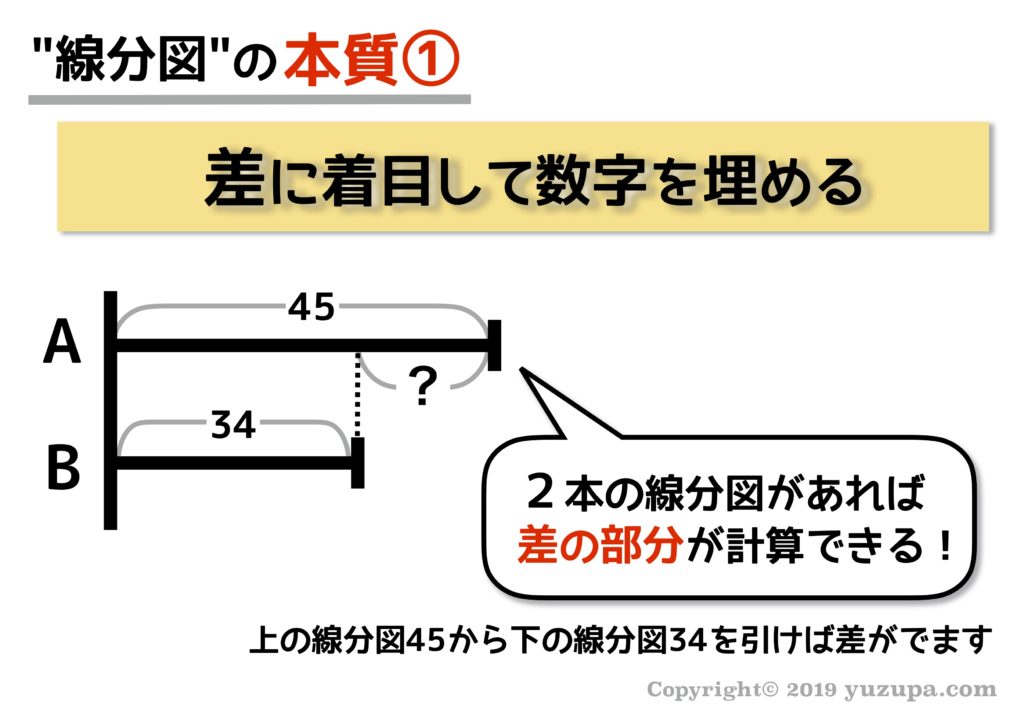
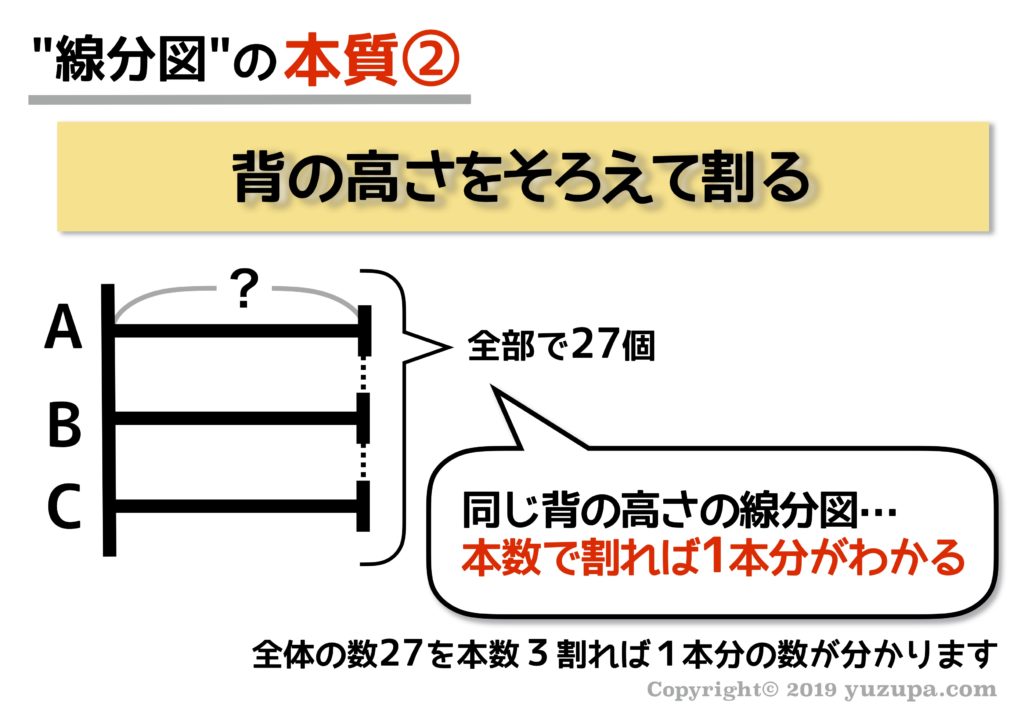
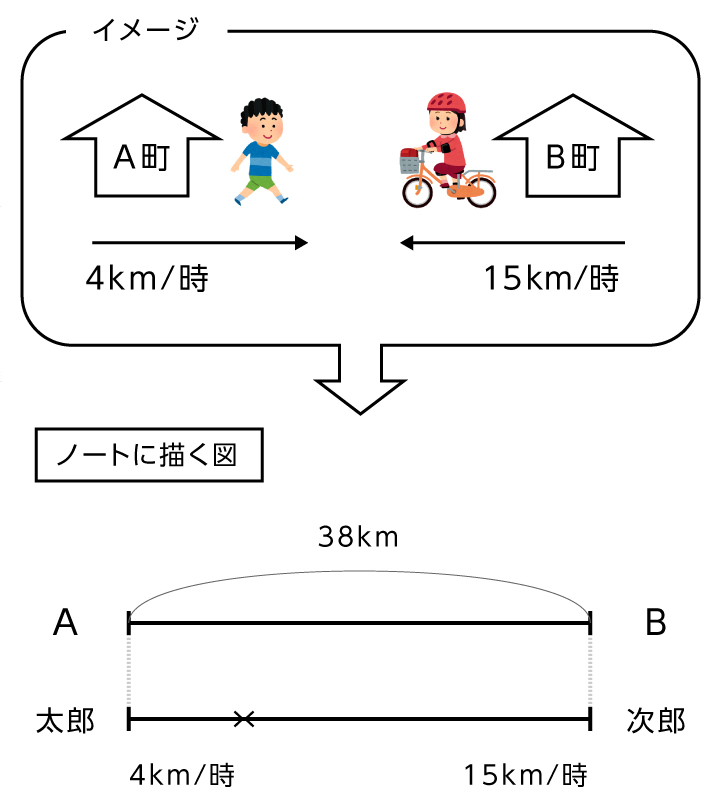
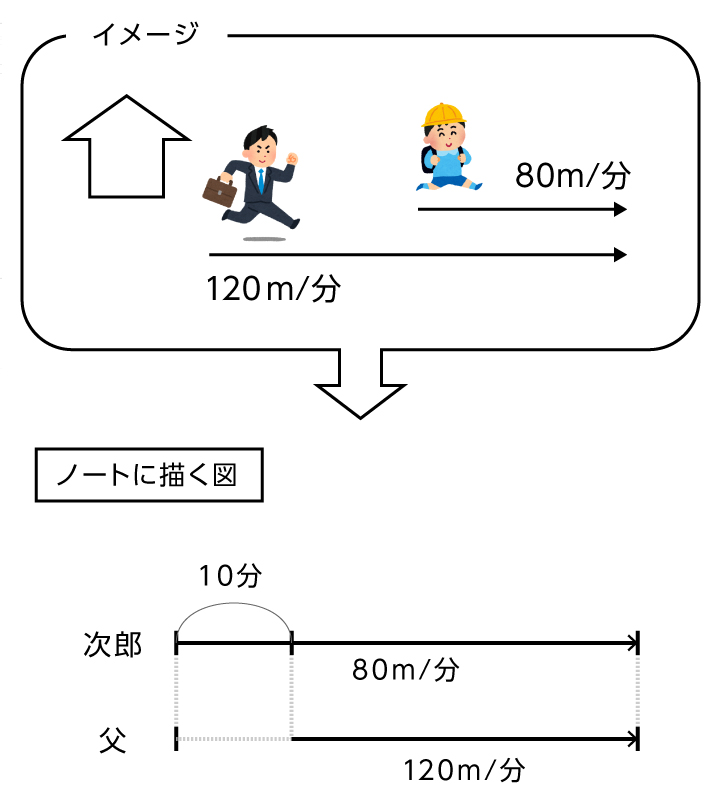
線分図を使った問題の解き方

問題を解くための全体の流れ

線分図を使って問題を解く場合、３つのステップで解いていくのが良い でしょう。最初のステップは、問題文をよく読みながら線分図を描く事。次に”本質①”を使って埋められる数字をトコトン埋める事。最後は”本質②”と”本質③”を使えないか試行錯誤する事です。

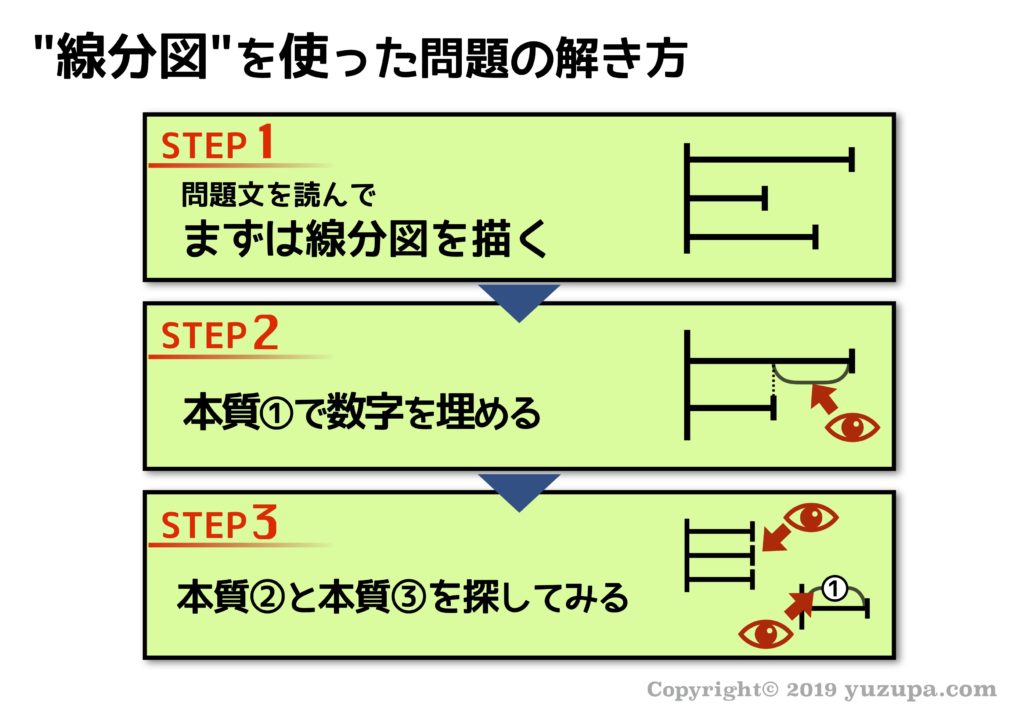
それでは順番に見てみましょう！

STEP1：問題を読み線分図を描く

まずは問題文をよく読みながら、線分図を描きます。問題文に使われている数字は問題を解くために必ず必要になる数字ですので、もっとも注意すべきことは数字の見逃しですd(^_^o)

ただ… 問題によって線分図を描くためのちょっとしたコツが必要です(-_-;) 特に年齢を扱う年齢算や、商売を扱う損益算は線分図を書く練習が必要 です。こちらについては過去の記事でも詳しく解説していますd(^_^o)

参考リンク：年齢算は”線分図の伸び縮み”で理解

参考リンク：損益算は”色付き線分図”を描け！

STEP2：本質①に注目して値を埋める

何本かの線分図を並べて描くと、必然的に”差”が浮き彫りになりますね！２つ目のステップは ”差”に着目してひたすら数字を埋めること です。これは本質①ですねd(^_^o)

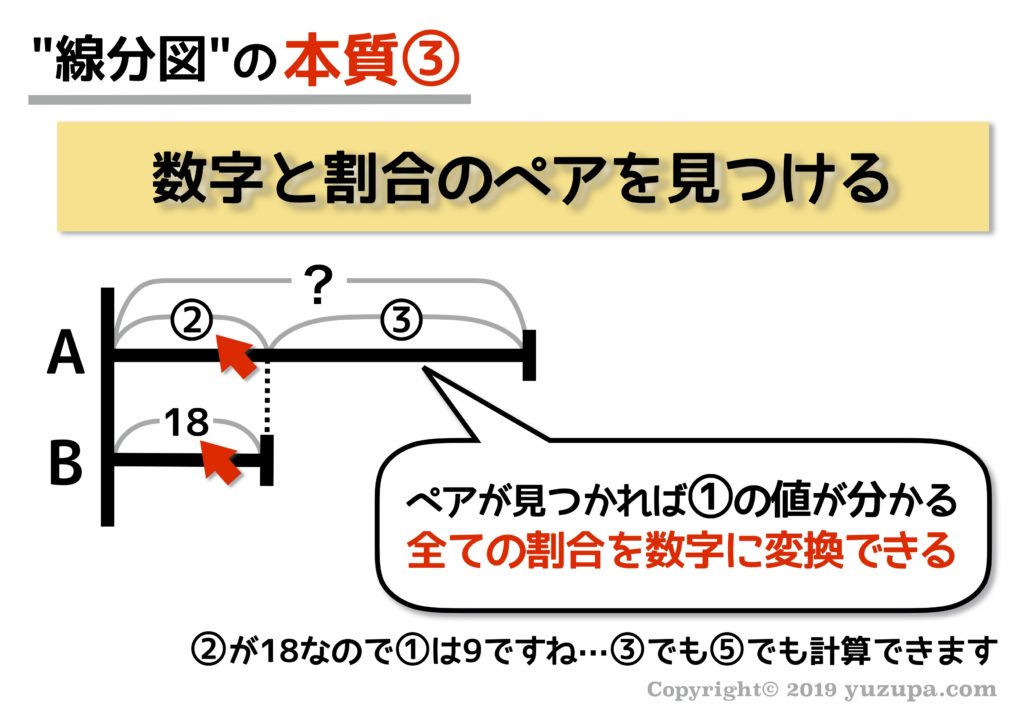
ここで注意すべきことは 実際の数値だけでなく割合も差を求めることができる という事です。そして割合は実際の数字と区別するために丸数字で書くということもポイントです！

STEP3：本質②と本質③を探してみる

最後はSTEP2までに出来上がった線分図を眺めて、本質②と本質③を使えるところがないか探してみます。背の高さを合わせられるところは無いか？丸数字と実数字がペアになっているところが無いか？

ここで 本質②や本質③を見つけることが出来れば解けたも同然 です！

ちなみに… STEP2とSTEP3は順不同 です。簡単なヒントから埋めていくのが一般的なので敢えて順序を描いてみました。当然、簡単な問題だとSTEP2までで解けてしまうこともあります(^_^;)

 

具体的な解き方の例

和差算の例

まずは和差算です。和差算とは２つの値の和と差が与えられている問題 です。解説サイトによっては不親切にも公式だけがポツンと書かれている場合がありますが、その公式は線分図を描かいて導き出した公式です(^_^;)

公式の暗記はその公式がなぜそんな式になっているか？ を理解しているのが大前提！公式の元ネタが分かっていれば応用問題が出されても対応できますd(^_^o) 逆に…単なる公式の丸暗記は応用が効かなくなるので注意を！

それでは問題をどうぞd(^_^o)

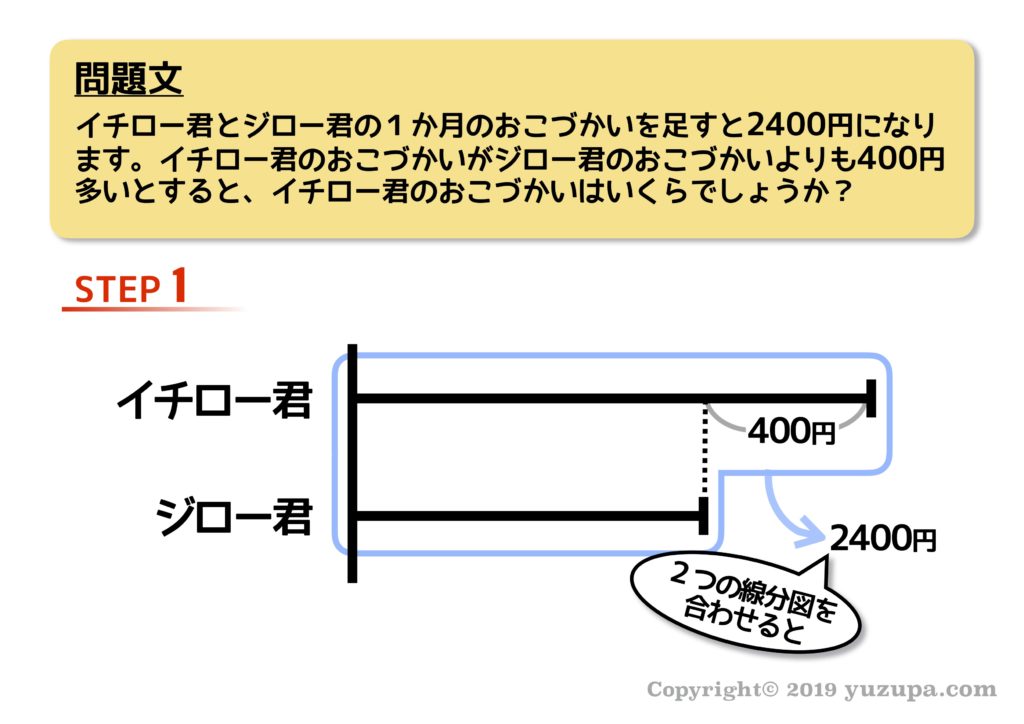
STEP1では問題文をよく読みながら線分図のベースを描きます。この問題の場合とてもシンプルですね！ 和の部分はこんな感じで線で囲んで描くのが良いでしょうd(^_^o)

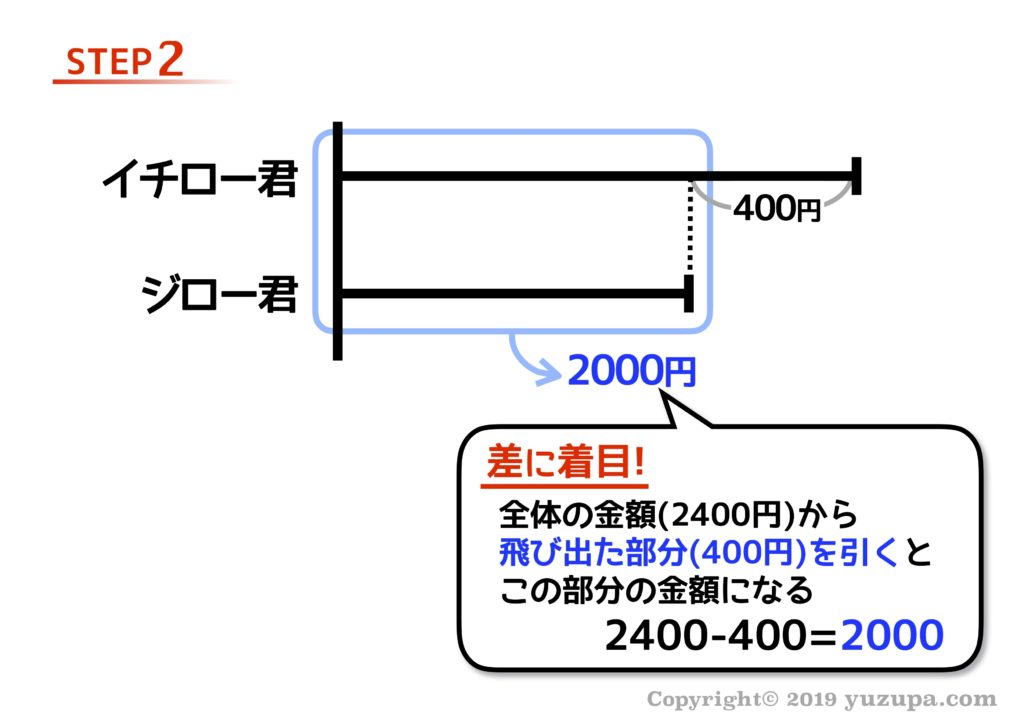
線分図に現れる”差”に着目 すると飛び出た部分以外の数字を出すことができますねd(^_^o)

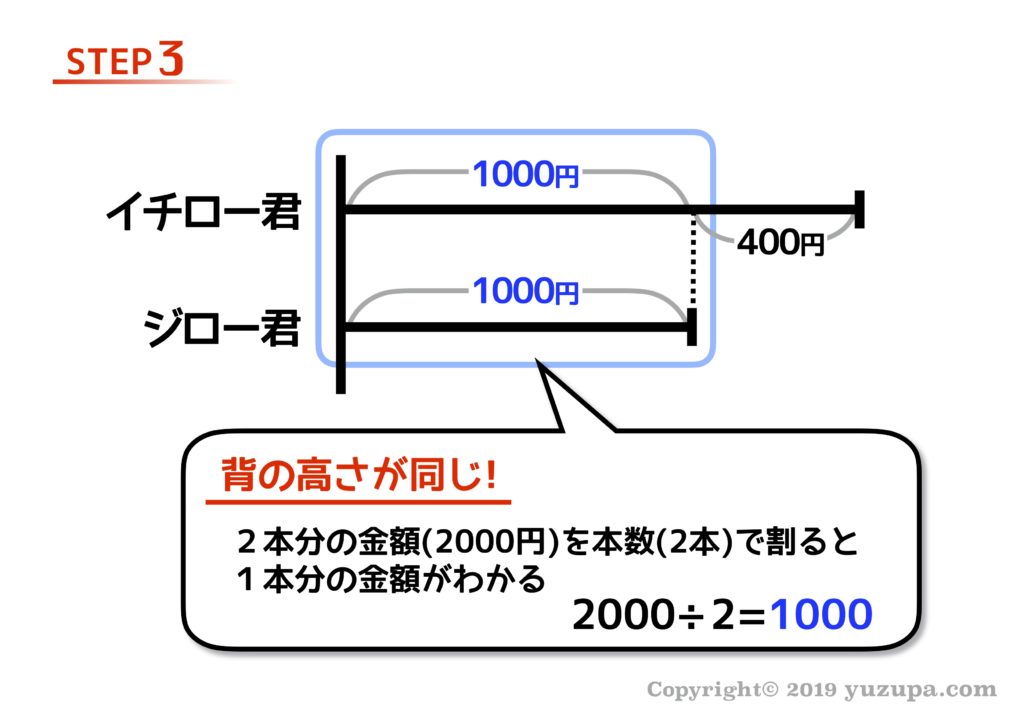
和差算ではだいたい本質②を使います。２つの線分図の高さをそろえてあげて２で割れば１本分の高さが分かりますねd(^_^o) ここまで来れば答えが出ます。イチロー君のおこづかいは、1,400円ですね！ ちょっと安い…。

 

分配算の例

次は分配算です。分配算とはアメ玉を複数の人に分配したり… お金をみんなで分けたり… 何かを複数の人に分配するときの条件が与えられている問題 です。せっかくなので今度は線分図が３本になる問題をd(^_^o)

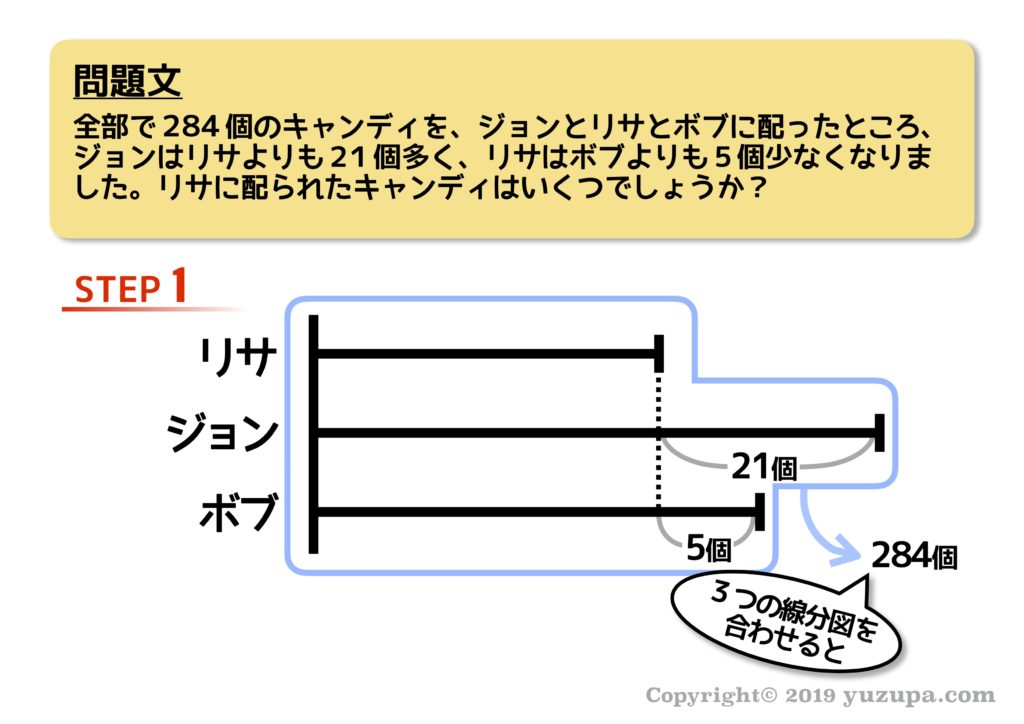
ここまでは問題文を読むことができれば描けるはずです。もし間違ってしまう場合は問題文を読むための国語力や、慌てず落ち着いて問題文を読む注意力の問題かもしれません。ちなみに我が家の場合… ”よーく問題を読め！”と何度も息子に注意しました(-_-;)

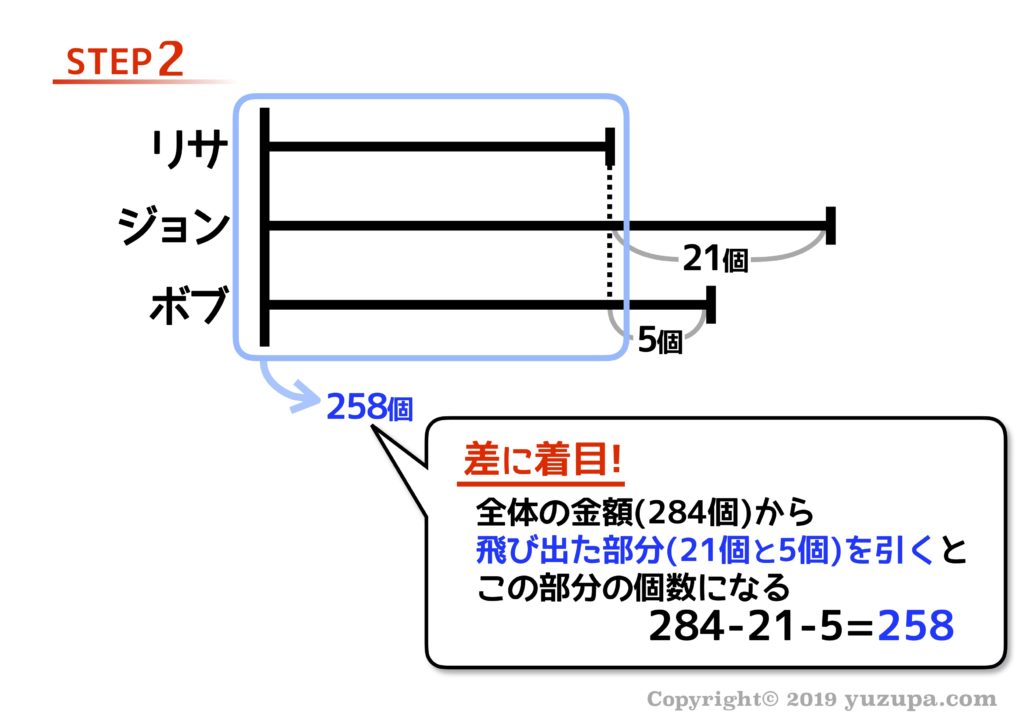
和差算とほぼ同様…　線分図を眺めながら”差”に着目する と出っ張った以外の部分の数字が分かりますd(^_^o)

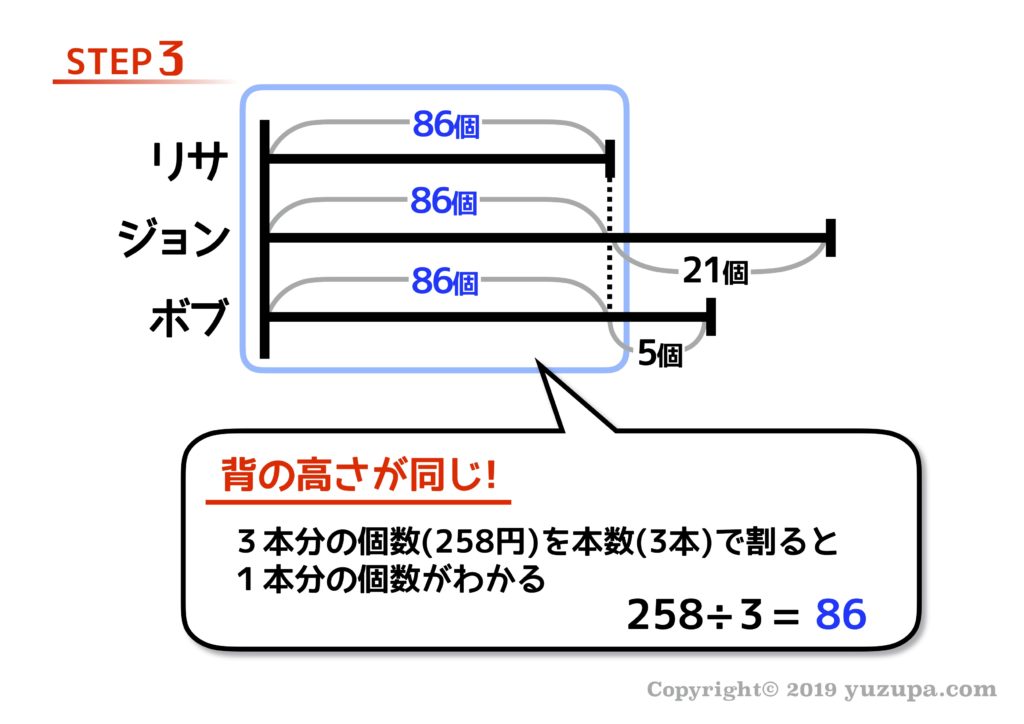
そうすると… 同じ高さの線分図３本が見つかりました！ 今度は線分図の数は３本ですので、３で割ってあげれば１本分の値を出すことができますねd(^_^o)

リサに配られたキャンディーは86個です！

年齢算の例

次は年齢算です。年齢算とは年齢を扱う問題です。年齢算も線分図の本質を使って難なく解けるのですが、ベースの線分図を描くのに、ちょっとコツが必要です。詳しくは こちらの記事 で解説していますのでご参照を！

それでは問題です。

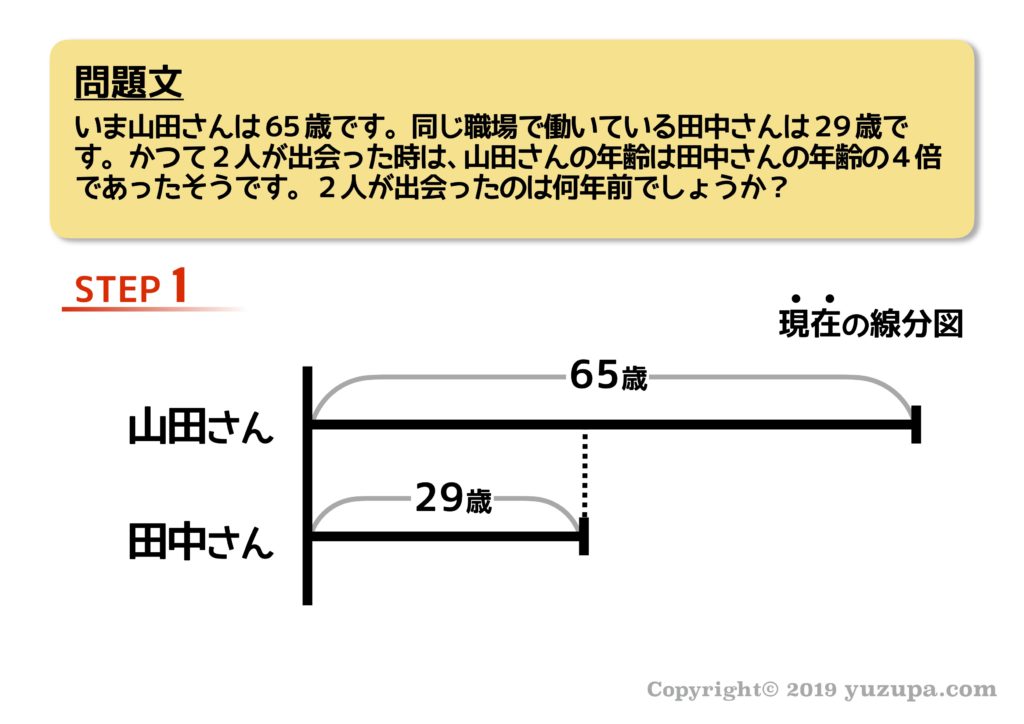
ここまでは問題を読めば誰でも線分図を描けますね。線分図を描く上での ポイントは “出会った頃”の線分図を描かなくてはならない事 です。こう描きます。

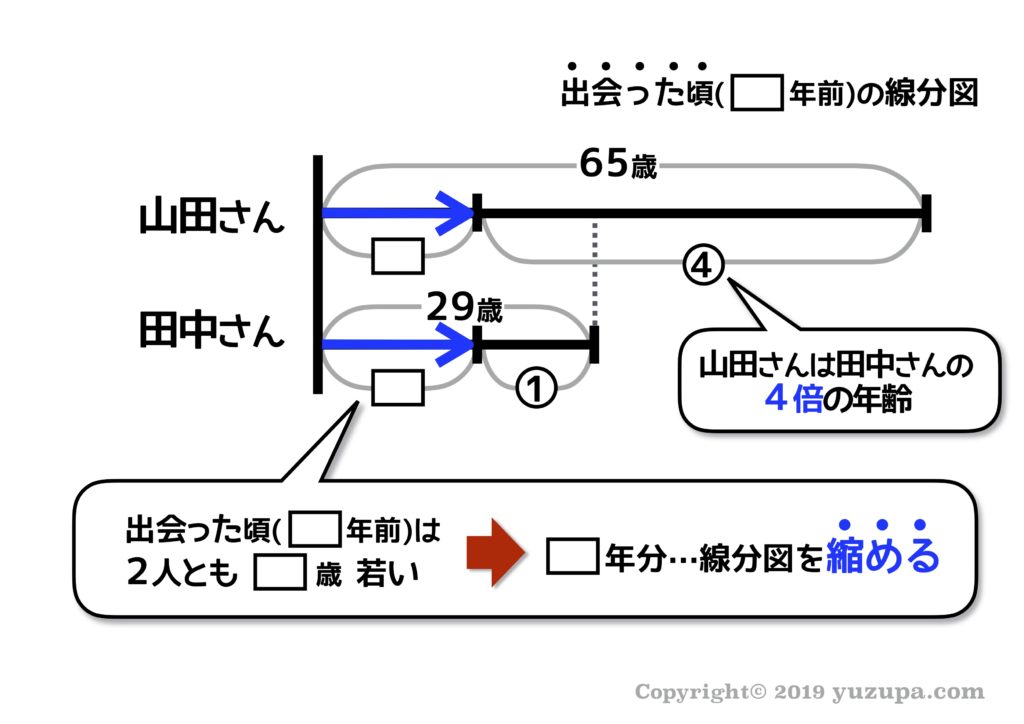
何年前か分かりませんが、過去の線分図を描く場合は同じ長さだけ線分図を縮める事でキレイな線分図を描くことができます。

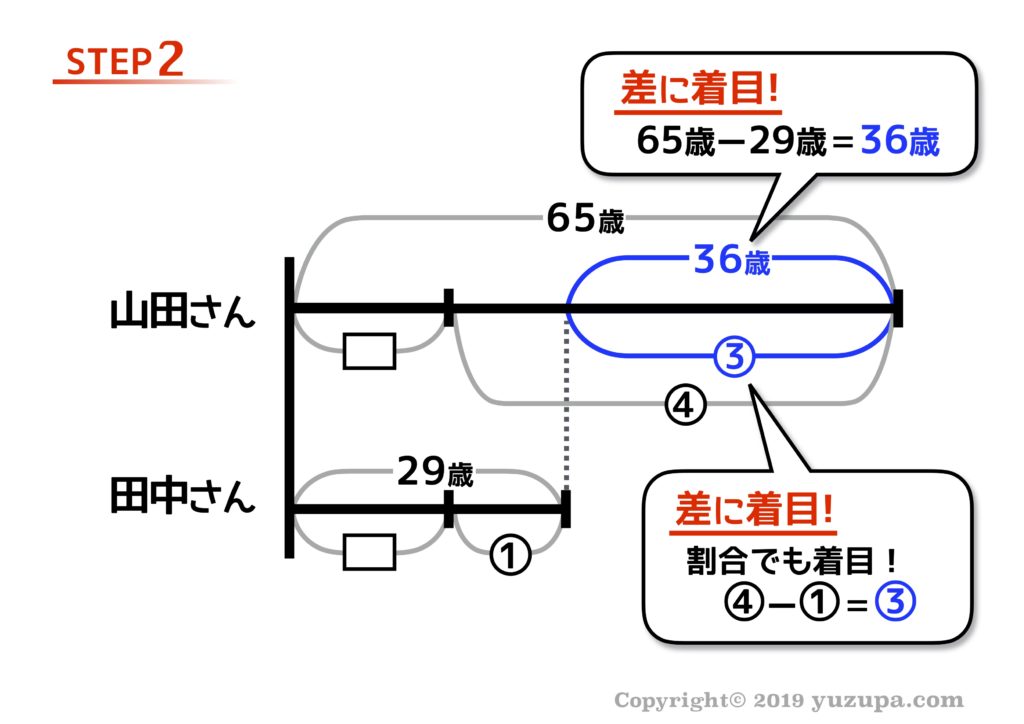
STEP2とSTEP3では、セオリー通り“差”が分かるところを片っ端から埋めてみましょうd(^_^o)

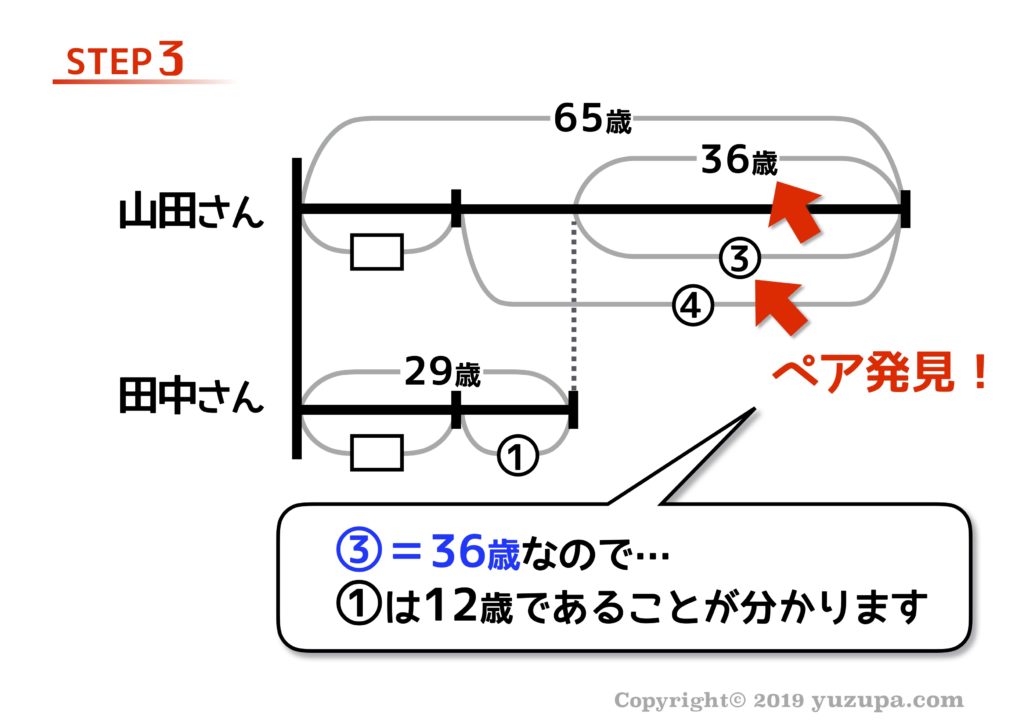
そうすると本質③の割合と数字のペアが見つかりますね∑(ﾟДﾟ)　割合と数字のペアが見つかったら、丸数字１つ分がいくつなのか計算をします。この問題の場合は①は12歳分ですね！

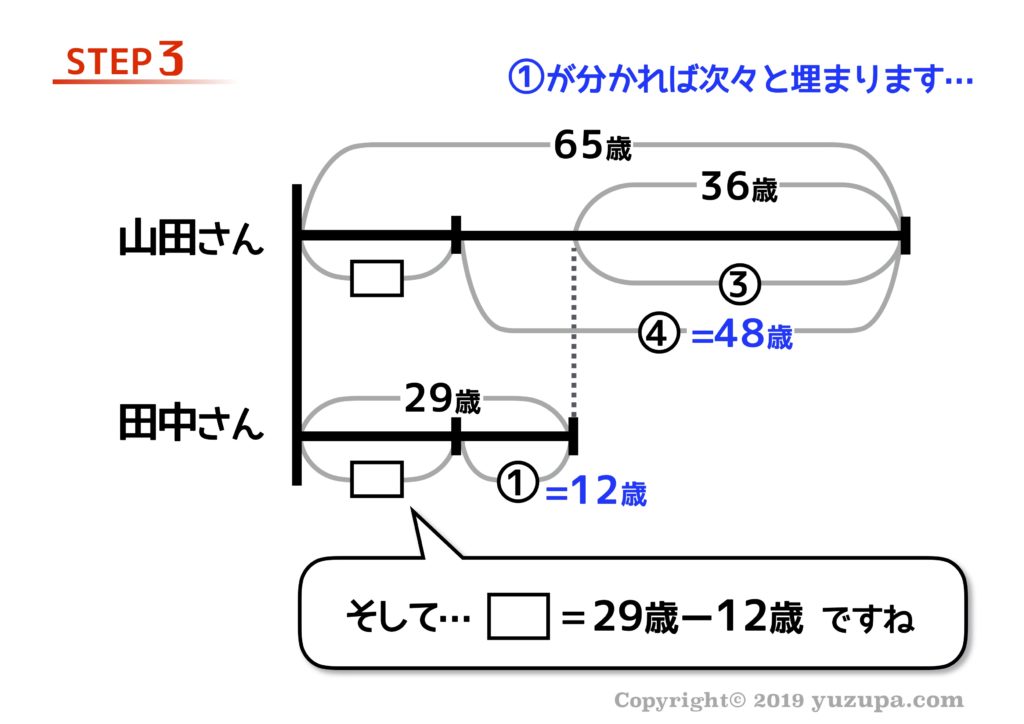
割合と数字のペアさえ見つかってしまえば 線分図の数字は一気に埋まります。出会ったのは田中さんが12歳の時。今から17年前ですね d(^_^o)

相当算の例

お次は相当算なるものです。相当算とは割合や比が登場すると同時に、いつくかの実数値が出る問題を総称して、そう呼ぶそうです(^_^;) 割合が出てくるので実数値とのペアを見つけることが出来れば、割合を一気に実数値に変えることができます。

それでは例題をどうぞ。

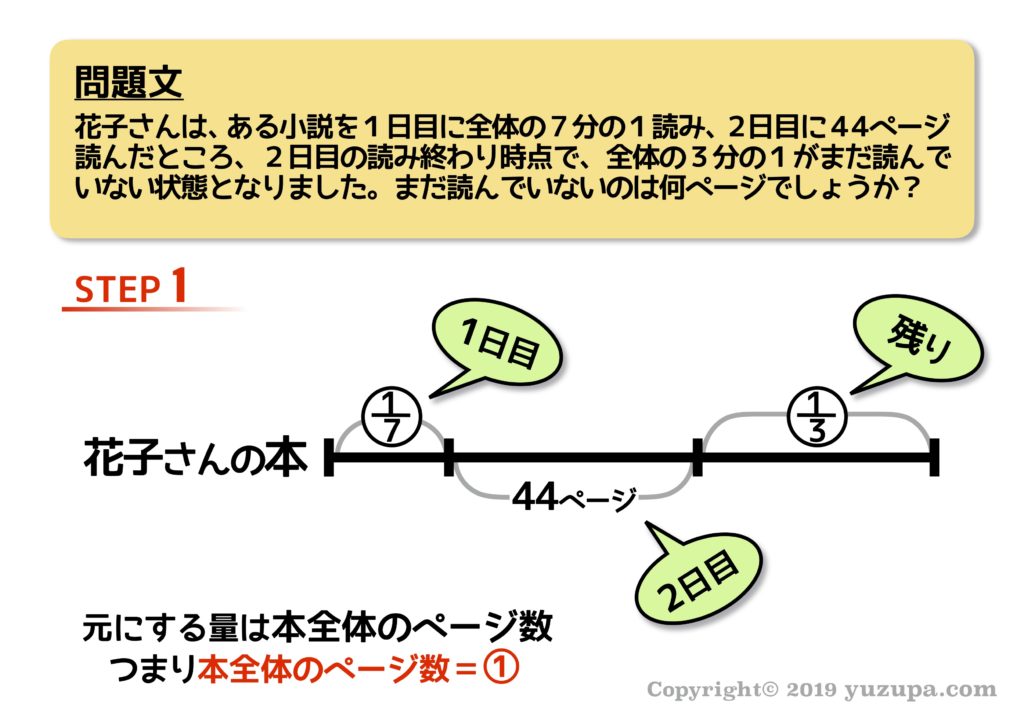
問題文を読みながらベースとなる線分図を書いていきますが、注意すべきは割合の”元になる数” です。何の７分の１なのか？ 何の３分の１なのか？しっかり意識しましょう。

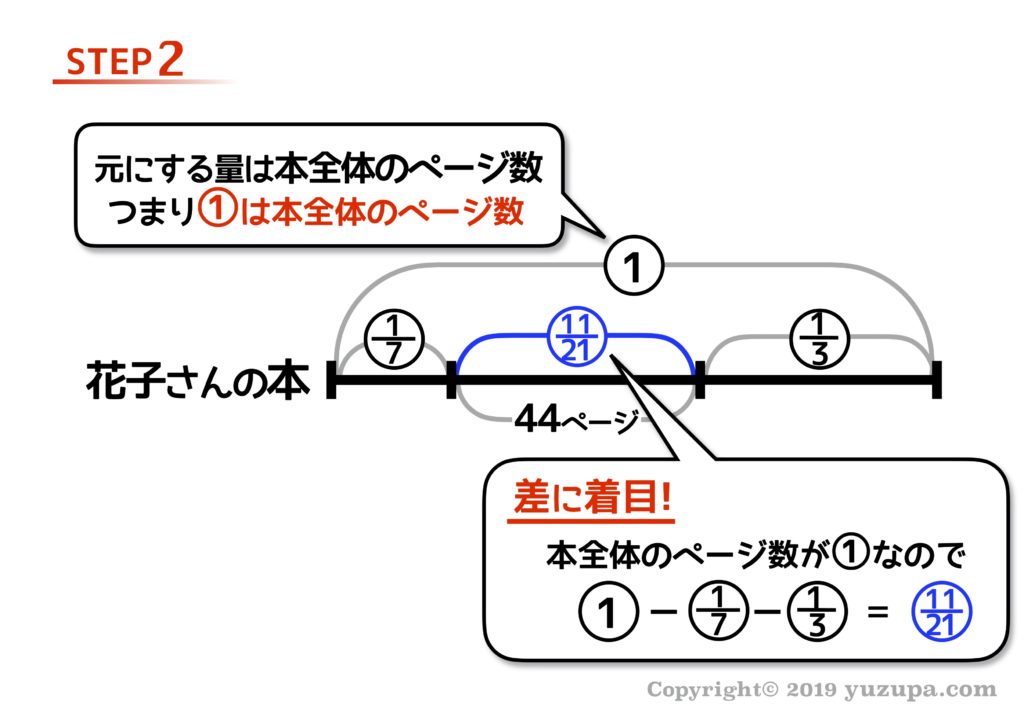
差に着目すると、２日目に読んだ部分の、割合が分かりますね。

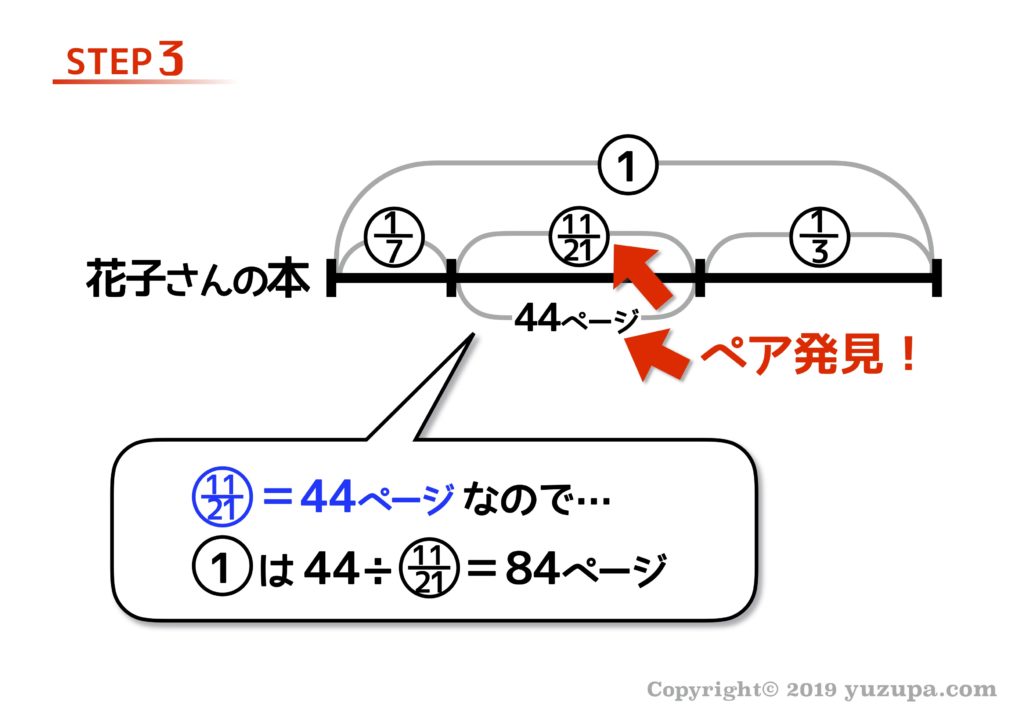
そして割合と数字のペアが見つかりましたd(^_^o) あとは割合をジャンジャカ実際の数字に変換させましょう！

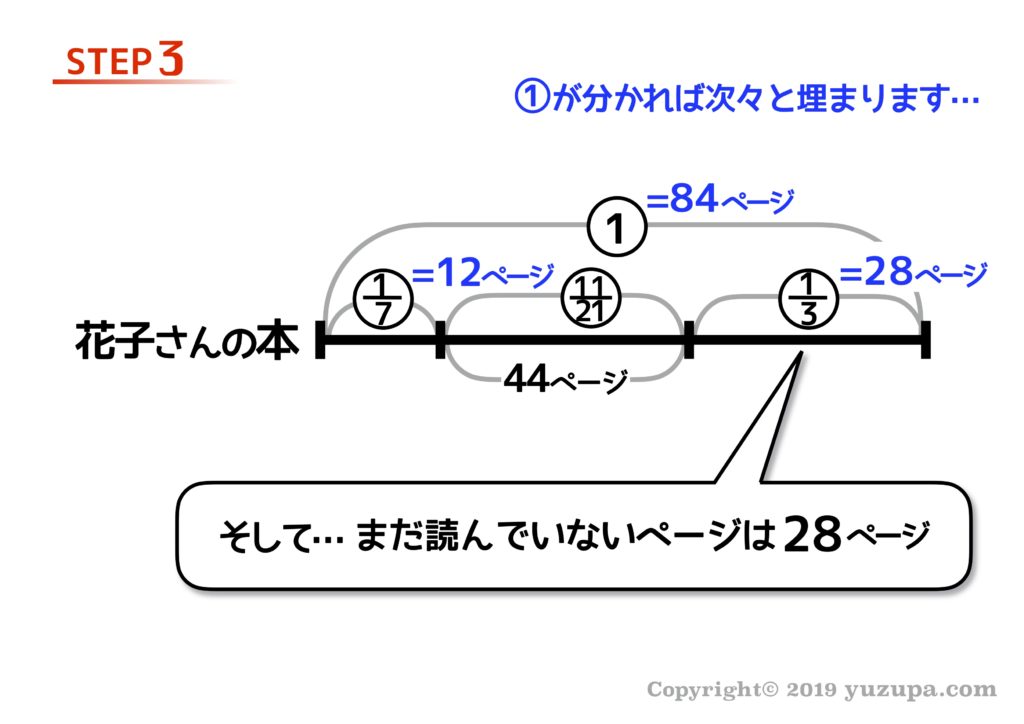
おのずと答えが導き出されます。この本のまだ読んでいないページ数は28ページですねd(^_^o)

倍数算の例

次は倍数算なるものです。倍数算とは倍数と実際の数字が出てきて答えを求める問題…。ん？どこかで聞いたような。そうです。相当算と定義がほぼ一緒です(^_^;)

ちなみに…先ほど紹介した年齢算も実は倍数算の一種です∑(ﾟДﾟ)

中学受験でやたら出てくる “特殊算” ですが、色々な有識者が考案しては世の中に浸透するという事を繰り返したため全く体系化されていません(^_^;) 解法を探るヒントくらいに思っておくのが良いかと思います。

では倍数算の例題をどうぞ。

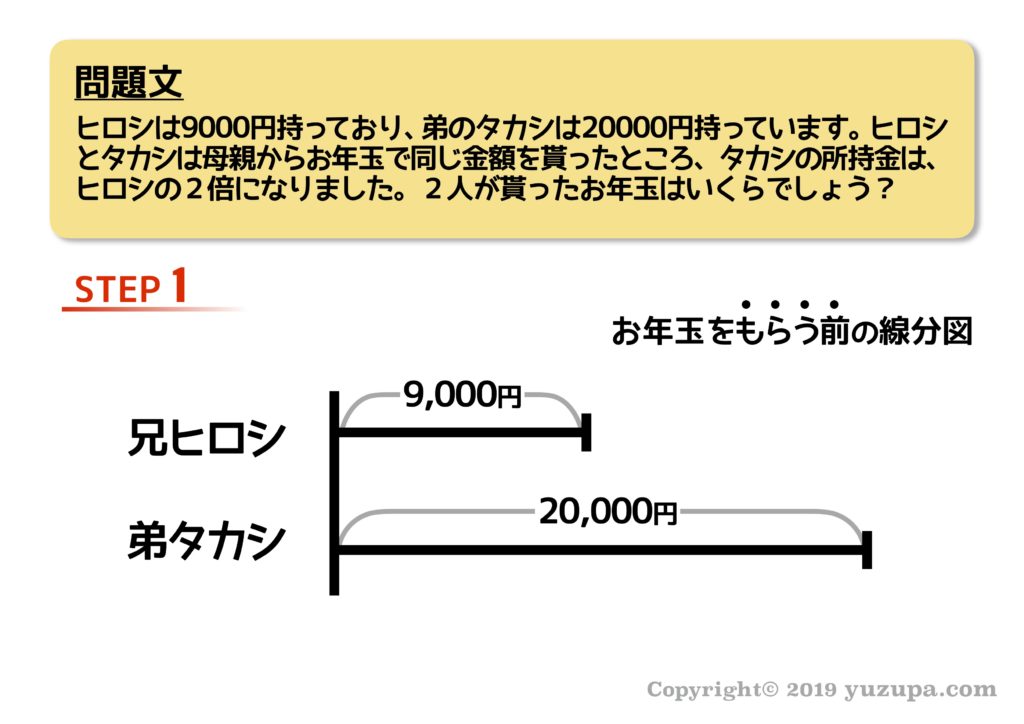
今までで最もシンプルな線分図ですね(^_^;) 兄の方が所持金が少ないのが気になりますが…ポイントはお年玉をもらったあとの線分図を描くところ ですd(^_^o)

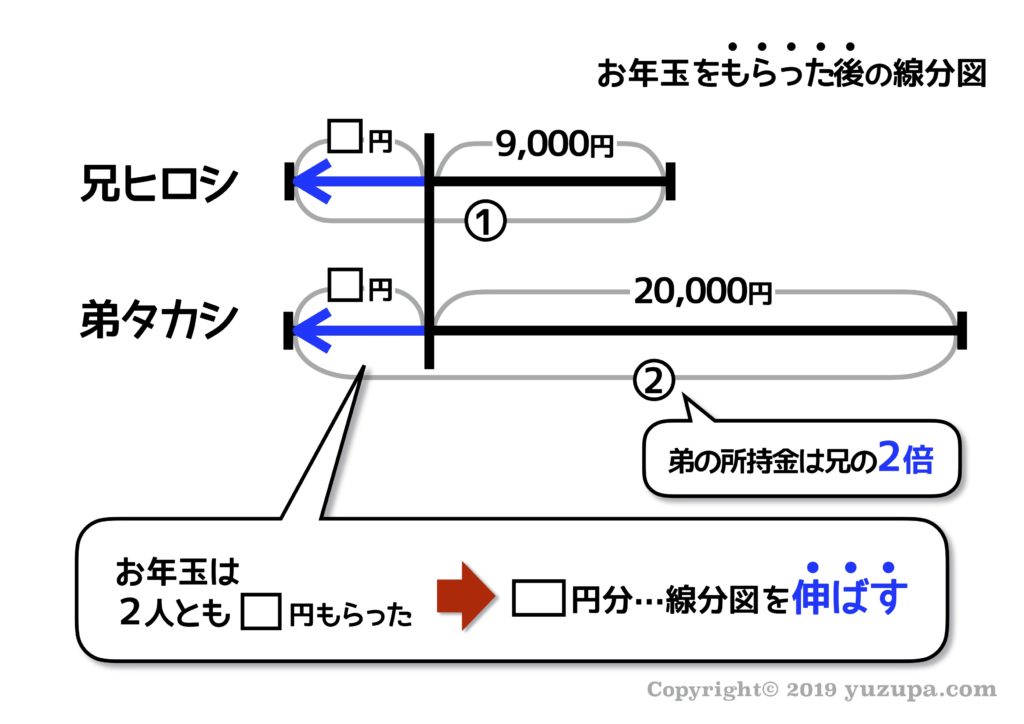
先ほどご紹介した年齢算と同じように線分図を伸び縮みさせます。今回は２人とも同じ金額をもらっているので 線分図を同じ長さだけ伸ばします d(^_^o)

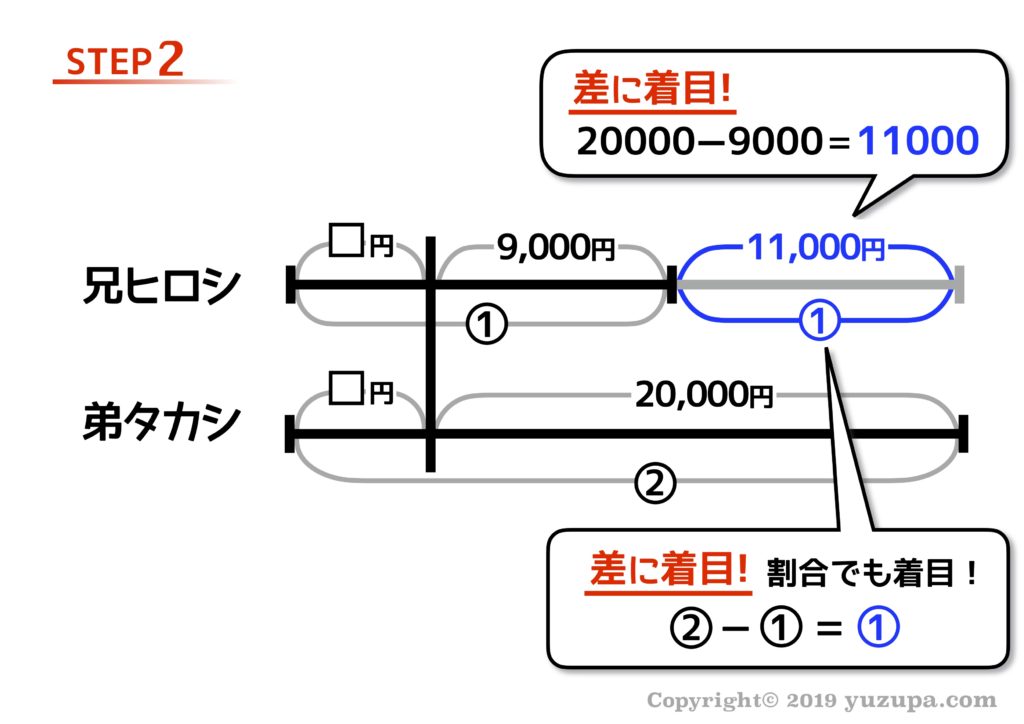
線分図が描けたらいつもどおり“差”を意識して線分図を埋めます。この問題の場合は、実数字の差もありますし、割合の差もありますねd(^_^o)

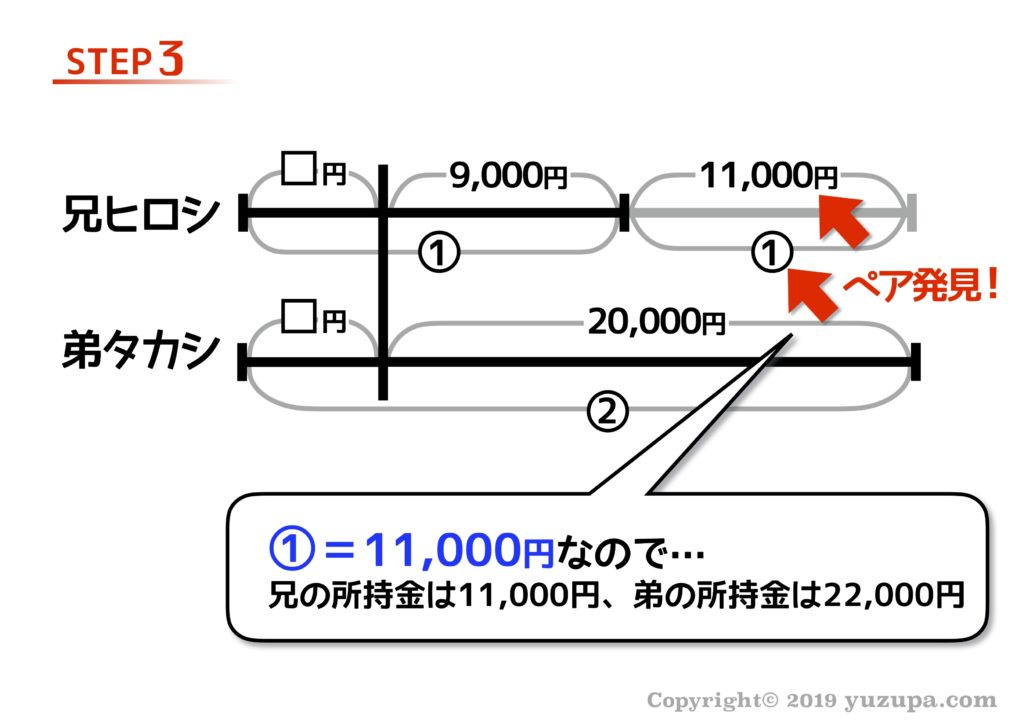
最後は割合と数字のペアが見つかりました。本質③ですねd(^_^o) ペアさえ見つかってしまえば、線分図の数値埋めはガンガン進みます。お年玉としてもらったお金は2000円 であることが分かります。

損益算の例

最後は損益算です。損益算というたいそうな名前がついていますが、売上や原価や利益を計算する問題を総称してそう呼んでいるようです(^_^;) さっそく例題を見てみましょう。

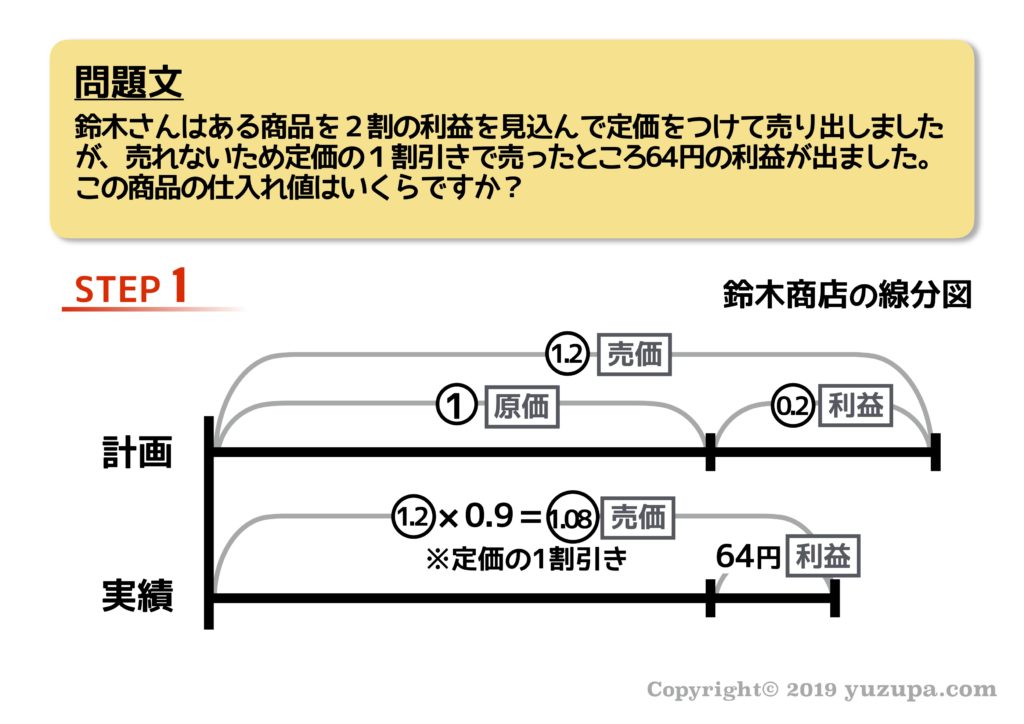
問題を読んで大人はこの線分図をスンナリ描けるのですが、子供は苦戦したりします(@_@) 私の息子の場合、原因は言葉の定義がイマイチだったためでした_φ(･_･

もしこの例題の線分図が描けない場合は、損益算で使ういわゆる”商売用語”を先に学習した方が良いかもしれません。こちらの記事 で詳しく解説していますd(^_^o)

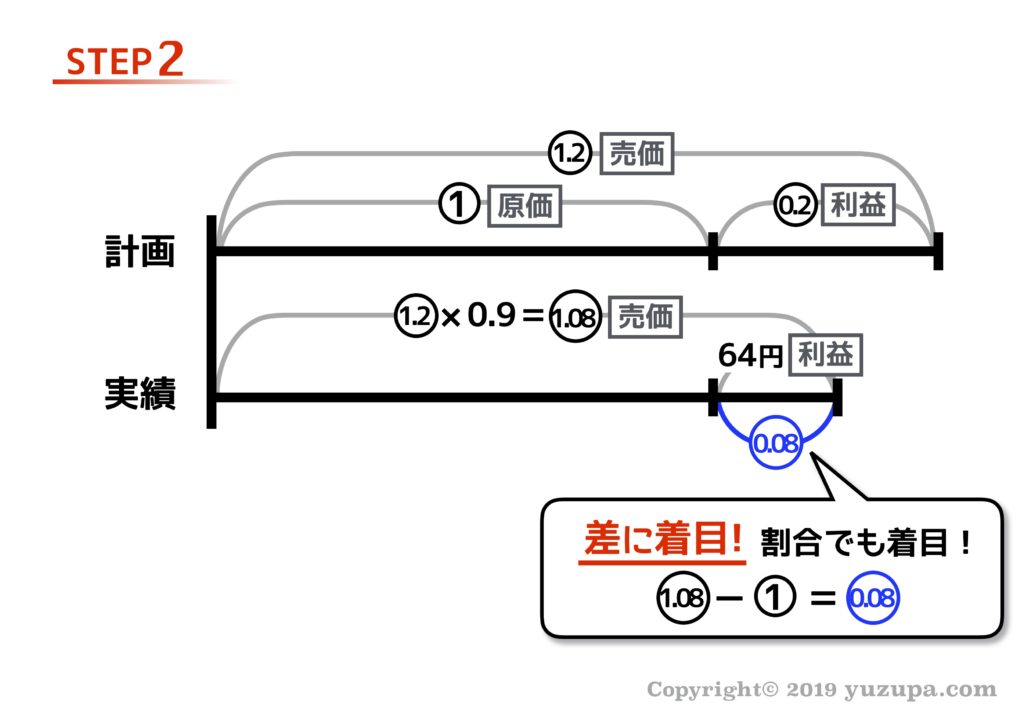
いつもどおり”差”に着目すると、割合と数字のペアが見つかりますねd(^_^o)

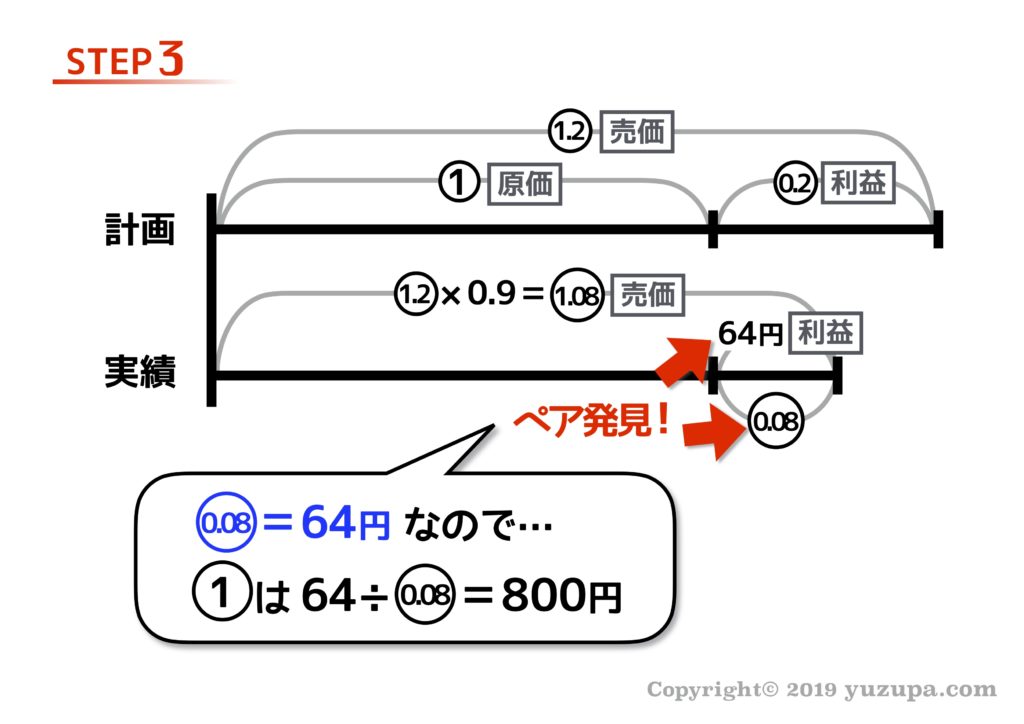
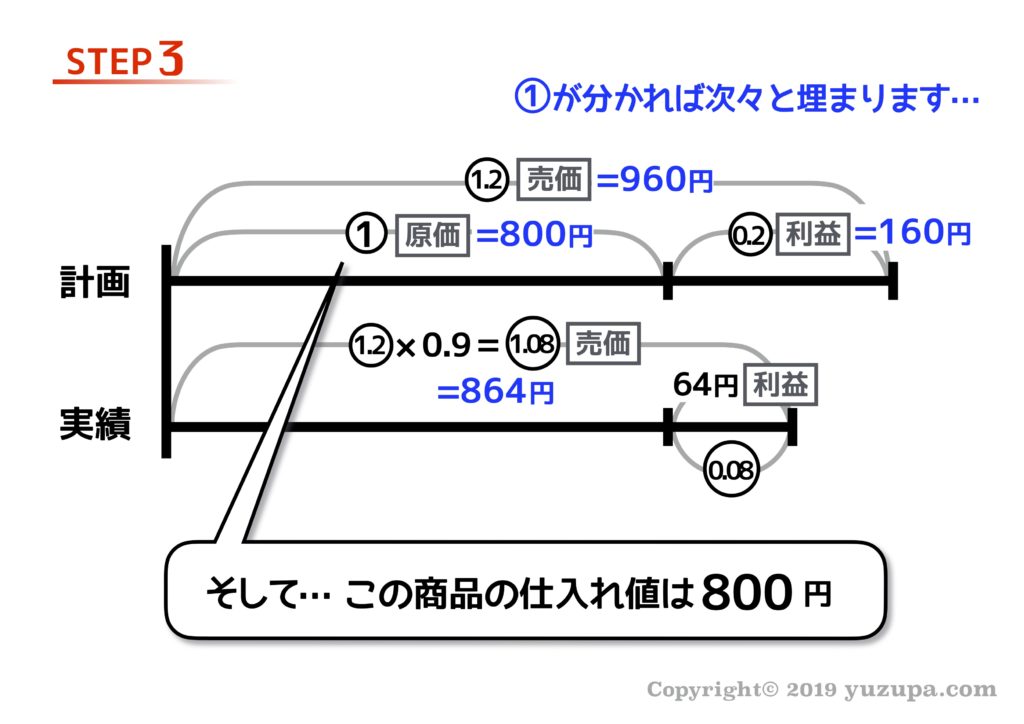
繰り返しとなりますが、ペアさえ見つかってしまえば線分図の大部分を埋めることができるようになりますd(^_^o)

 

 

まとめ

中学受験で登場する”線分図”という謎のツールの基本から、実際の例題を通して使い方をまとめてみました。例題も全て読んでいただいた方は お気づきかと思いますが実は超シンプルです…

言い換えると、たった３つの本質をビジュアルにとらえるために線分図があるようなものですd(^_^o) ６つの特殊算の解法としてご紹介しましたが大切なのは ３つの本質を意識して線分図を眺めることです！

① 線分図はどんな時に使う？
　和差算・分配算・年齢算・相当算・倍数算・損益算の６つの特殊算

② 線分図のたった３つの本質
　１. 差に着目して数字を埋める
　２. 背の高さをそろえて割る
　３. 数字と割合のペアを見つける

 

線分図 中学算数 前半

中学受験：線分図はいつ使う？ たった３つの本質で解ける

中学受験の世界の謎のツール”線分図”…実はたった”３つの本質”で解ける超シンプルなもの

中学受験の独特な世界観… 江戸時代の鶴亀算からはじまり塾の先生方が作り上げた ナントカ算（別名：特殊算）という算数問題を解くための体系… そこで使うツールが “線分図” です。

“線分図”という名前がついてはいますが…実は単なる棒グラフです(^_^;) それでも色々な問題で使われるので子供達は “どんな時に使ったらよいのか？どうやって使ったらよいのか？” 混乱している模様(@_@)

でも問題を子供と多数といていると
実はとってもシンプルなものであることが分かりますd(^_^o)

① 線分図はどんな時に使う？
　和差算・分配算・年齢算・相当算・倍数算・損益算の６つの特殊算

② 線分図のたった３つの本質
　１. 差に着目して数字を埋める
　２. 背の高さをそろえて割る
　３. 数字と割合のペアを見つける

ちなみに… こちらの記事 でも紹介しておりますが、”特殊算” とは塾の先生を中心とした有識者が算数の解法を考案しては名前をつけ…浸透したもの。実はバラバラで体系的ではありません(^_^;)

 

スポンサーリンク

目次 [非表示]

• 1 線分図とは？
  • 1.1 線分図とは何か？
  • 1.2 線分図の利点は？
  • 1.3 線分図を使うべき６分野
  • 1.4 線分図を使うための “３つの本質”
• 2 線分図を使った問題の解き方
  • 2.1 問題を解くための全体の流れ
  • 2.2 STEP1：問題を読み線分図を描く
  • 2.3 STEP2：本質①に注目して値を埋める
  • 2.4 STEP3：本質②と本質③を探してみる
• 3 具体的な解き方の例
  • 3.1 和差算の例
  • 3.2 分配算の例
  • 3.3 年齢算の例
  • 3.4 相当算の例
  • 3.5 倍数算の例
  • 3.6 損益算の例
• 4 まとめ

線分図とは？

線分図とは何か？

線分図とは… 数字を横軸にとった模式図です。左端をそろえて描くことが一般的ですので 複数の棒グラフが並んでいると思ってしまって差し支えありません(^_^;) 実際の例題で簡単な線分図を描いてみましょう。

太郎くんの所持金は1200円で、二郎くんの所持金は500円、三郎くんの所持金は二郎くんの２倍です。この線分図を描いてみると以下のようになります。ほら…とてもシンプルな棒グラフですねd(^_^o)

線分図の利点は？

さて線分図というものは シンプルな棒グラフ であることが分かりましたが…これって何が嬉しいのでしょうか？ 面積図の記事でも同様の事をお伝えしましたが 方程式を使わなくても問題が解けてしまう事…

えぇ…こんなもの覚えるより、小学生と言えども１次方程式くらいなら教えてしまった方が良いのでは？と…思いますよね (^_^;) ただ方程式を教えずに敢えて “線分図” を使うことには以下のメリットがあります。

方程式であっても式を立てるところまでは小学生でも簡単にできるんです。でも…  “負の数”が出てきたり…”文字式”の計算が出てきたり… 方程式は結構な ”計算力” が必要なため思った以上にハードルは高い です ∑(ﾟДﾟ)

ためしに…簡単な例題を “方程式” と “線分図” で解いて比較してみましょう。式は立てられても方程式を計算ミスなく解けるように練習するのは骨が折れそうです。

線分図を使うべき６分野

小学生に方程式を教えるのはハードルが高いから…といって多くの特殊算が考え出された結果、どんな時に線分図を使うと便利なのかを判別できなくなるという課題 が出てきました…∑(ﾟДﾟ)

パーフェクトな答えはありませんが、以下の６つの特殊算は線分図を使うと概ねうまく解けますd(^_^o) 問題を多くこなせば “こういう問題は線分図だ” という感覚ができあがりますが、まずはこの６つを線分図で！

線分図を使うための “３つの本質”

さて…最後は線分図を使う事の本質に触れたいと思います。線分図を描いた後に… この３つの本質を使って数字を埋める事こそが線分図を使った解法の全て なんです d(^_^o)

本質①： 差に着目して数字を埋める
線分図の正体は棒グラフでしたね？ 棒グラフで最も視覚的にわかるのは “差” です。線分図を描けば いろんな値の差が手に取るように分かりますよね。これこそが線分図を描く事のメインの目的です。

本質②： 背の高さをそろえて割る
線分図の高さをそろえる事ができれば割り算をすることができるという点が２つ目の本質です。ちょっとイメージしにくいかと思いますので例をもとに見てみましょう。

本質③： 数字と割合のペアを見つける
こちらの記事 でも紹介しましたが、割合と数字のペアが１組でも見つかると一気にゴールに近づく事ができます。あらゆる割合の実際の数字を求めることができます。線分図でも同様ですねd(^_^o)

 

 

 

中学算数 わりあま

【ナルホド・ザ・中学受験算数】

今回は割り算の割る数と余りから割られる数を突き止める問題（条件式2本）です。

[問題]6で割ると2余り、8で割ると4余る整数があります。このような整数のうち、2ケタでもっとも大きい整数はいくつですか？

[考え方]写真の2つの式をご覧ください。この問題では両方の式で「割る数と余りの差」が4（青色）にそろっていることが大事なポイントです。求める整数□があと4大きければ、6でも8でも割り切れるはずです。すぐにピンとこなければ、1つめの式で簡単な数を考えてみてください。たとえば8÷6＝1あまり2ですが、割られる数が4増えて12になれば割り切れますね。2つめの式でも同じことです。このことを整理して言い直すと、求める整数□は、6と8の公倍数より4小さい整数ということになります。公倍数とは「最小公倍数の倍数」だから、6と8の公倍数とは24の倍数のことで、求める整数□は24の倍数より4小さい整数なのです。2ケタでもっとも大きいという条件を加味すると、24を4倍した96から4を引いた92が正解となります。

[解答]92

解説

本問は「割る数と余りの差がそろっているタイプ」ですが、他には「余りだけがそろっているタイプ」「特にそろっているものがないタイプ」もあります。

[お宝公式]★割る数と余りの差がそろっているとき→割られる数＝割る数の公倍数－そろっている差

方陣算 中学受験 中学算数

方陣算がおもしろい！ 正方形の形に並べた碁石の数を上手に数えてみよう

 

 

「方陣」という言葉をご存知ですか？ 算数に登場する方陣として有名なのは「魔方陣」でしょう。魔方陣とは、数字を縦と横に同じ数だけ並べて、横・縦・斜めの和がすべて等しくなるようにした問題をいいます。中学受験算数でも魔方陣を時々見かけます。

しかし、それよりも出題頻度が高いのは「方陣算」です。方陣算は、正方形の形に並べた碁石の数を数える問題です。今回は、この方陣算について解説します。

Contents [hide]

• 中実方陣と中空方陣の考え方を理解しよう
  • 中実方陣のすべての碁石の数は平方数になる
  • 中空方陣では4つの角に位置する碁石に注意する
• 黒い碁石と白い碁石を並べる方陣算の問題を解いてみよう
• 碁石を三角形や五角形などの形に並べる問題もある

中実方陣と中空方陣の考え方を理解しよう

方陣算には、碁石が中までぎっしりつまった中実方陣と、中の碁石が取り除かれている中空方陣の2種類があります。

それぞれの方陣算について、どのように考えればいいのでしょうか？

中実方陣のすべての碁石の数は平方数になる

碁石が中までぎっしりつまった中実方陣では、（縦の碁石の数）×（横の碁石の数）＝（すべての碁石の数）になります。ここで（縦の碁石の数）＝（横の碁石の数）なので、（すべての碁石の数）は1、4、9、16、…という平方数になります。このことをふまえて、次の問題を解いてみましょう。

下の図は、あるきまりに従って碁石を並べたものです。10番目に並んでいる碁石の数は全部で何個ですか。

「あるきまり」がどのようなものかを考えます。1番目に並んでいる碁石は全部で4個です。同じように、2番目は9個、3番目は16個です。このことから、n番目に並んでいる碁石の数は全部で（n＋1）×（n＋1）で表されることがわかります。したがって、10番目に並んでいる碁石の数は全部で11×11＝121（個）です。

すべての碁石の数を数えるだけなら簡単でした。一方、周りに並んでいる碁石の数を数える場合、中空方陣になるので、少しだけ難しくなります。中空方陣については、次で解説します。

中空方陣では4つの角に位置する碁石に注意する

中の碁石が取り除かれている中空方陣では、正方形の4つの角に位置する碁石をどうするかがポイントです。次の2つの考え方があります。

4つの角に位置する碁石の数も数える方法（上図：左）では、5×4＝20（個）を求めた後、4つの角に位置する碁石4個を引きます。したがって、20－4＝16（個）となります。

一方、4つの角に位置する碁石の数を数えない方法（上図：右）では、初めから角に位置する碁石を外して計算します。したがって、4×4＝16（個）です。

どちらの考え方を使っても同じ答えになりますので、好きな方で計算するといいでしょう。

下の図は、あるきまりに従って碁石を並べたものです。一番外側のひとまわりに60個の碁石が並んでいるのは何番目ですか。

4つの角に位置する碁石の数も数える方法で考えます。n番目の正方形の一辺に並んでいる碁石の数を□とすると、n＋1＝□です。□×4－4＝60なので□＝16です。したがって、n＋1＝16となってn＝15（番目）が答えです。4つの角に位置する碁石の数を数えない方法でも同じ答えになることも確かめてみてください。

 

黒い碁石と白い碁石を並べる方陣算の問題を解いてみよう

方陣算の中には、黒い碁石と白い碁石を規則的に並べていく問題もあります。次の問題を考えてみましょう。

下の図は、あるきまりに従って碁石を並べたものです。このとき、11番目には、黒い碁石と白い碁石がそれぞれ何個ずつありますか。

白い碁石が1番目、3番目、5番目、…と奇数番目で増えていくので、まずは白い碁石の個数を求めることにします。白い碁石の個数を書き出してみます。

・1番目…3（個）
・3番目…3＋7（個）
・5番目…3＋7＋11（個）
・7番目…3＋7＋11＋15（個）
・9番目…3＋7＋11＋15＋19（個）
・11番目…3＋7＋11＋15＋19＋23（個）

これより、11番目の白い碁石の数は、3＋7＋11＋15＋19＋23＝78（個）です。実際に書き出してみると規則性（一番外側の白い碁石の個数は、4ずつ増える等差数列になっている）がわかって、簡単に個数を求められます。

一方、黒い碁石の個数は、（すべての碁石の個数）－（白い碁石の個数）で求めます。11番目のすべての碁石の個数は12×12＝144（個）なので、11番目の白い碁石の個数は144－78＝66（個）です。

方陣算では、まずは数字を書き出してみて、そこから規則性を考えましょう。碁石の数が等差数列になっていることが多いので、問題によっては等差数列の公式も使えます。

碁石を三角形や五角形などの形に並べる問題もある

方陣算の類問には、碁石を三角形や五角形などの形に並べる問題もあります。どのような形になっても考え方は同じだということを理解できると、

方陣算がさらに楽しくなるでしょう。

 

旅人算 中学受験 令和二年 皇紀2680年

 

旅人算とは――中学受験ではどんな扱い？

旅人算とは、「速さ」の単元の問題の一種で、複数の人がでてきます。さまざまなバリエーションがあるのが特徴で、「駅にむかった母親を、自転車で追いかける」「池の周りを逆向きに走って出会う」といった問題が出題されます。

かなり複雑な問題もあり、特に難関校を受けるお子さんは対策が必須です。旅人算は速さの計算が身についていないと解けないので、あらかじめ、「速さ」「時間」「距離」を自由に使いこなせるようにしておきましょう。

 

旅人算の基本的な解き方

旅人算の基本的なパターンは「向かい合わせで出発する」パターンと、「追いかける」パターンです。それぞれの解き方を解説します。

旅人算の基本パターン1――向かい合わせで出発

■例題1
A町とB町の間は38km離れています。太郎君はA町から時速4kmで歩き始め、花子さんはB町を時速15kmの自転車で出発しました。2人が同時に出発すると、出発してから何時間後に出会うでしょうか。

まずは、状況を図にします。

【図1】

太郎君は1時間に4km、花子さんは1時間に15km進むので、2人合わせて1時間に

4＋15＝19km

進みます。

2人合わせて38kmの道のりを進めばよいので、かかる時間は

38（km）÷19（km/時）＝2時間

となります。

旅人算の基本パターン2――追いかける

■例題2
次郎君は午前7時に、毎分80mで家から学校に向かいました。10分後に、家にいたお父さんが忘れ物に気がつき、毎分120mで走って追いかけました。何時何分に、お父さんは次郎君に追いつくでしょう。

状況を図にします。

【図2】

次郎君が出発してからお父さんが忘れ物に気づくまで、次郎君は

80（m/分）×10（分）＝800m

進んでいます。

お父さんと次郎君の速さの差は

120（m/分）－80（m/分）＝40（m/分）

です。

800mの距離を、40m/分で近づいていくので、

800（m）÷40（m/分）＝20（分）

午前7時10分にお父さんは家を出発しているので、

午前7時10分＋20分＝午前7時30分

に2人は出会います。

旅人算の問題には、2人が「池の周りを回る」などの形もあります。しかし、何かの周囲を回る問題も、ここで紹介した2パターンが基本です。まずは、「向かい合う」「追いかける」という2つの基本をおさえましょう。

旅人算で子供がつまずきやすいポイントとその対策

旅人算で子供がつまずきやすいポイントは、大きく分けて3つあります。

［1］図が描けない
［2］処理方法がわからない
［3］応用問題に対処できない

それぞれの対策を見ていきましょう。

［1］図が描けない

旅人算を解くうえで、図を描くことは非常にとても重要です。図を描かないと、状況が理解できないからです。

まずは【図1】【図2】の「イメージ」のような絵で、何が起きているのかを想像させましょう。そこから図を描くトレーニングをします。

図の描き方もパターンがあります。繰り返し解いていくうちに、「このパターンは、この図だな」とわかるようになります。

［2］処理方法がわからない

「図は描けているのに、その後の処理がわからない」といった場合、そもそも図の意味が理解できていないことがあります。もう一度、和差算にさかのぼって、図を使った解き方を復習しましょう。

また、旅人算はそもそも速さの計算がスムーズにできないと、図を描いても処理できないことがあります。お子さんが速さの計算でつまずいている場合は、そちらを優先的にフォローしましょう。

［3］応用問題に対処できない

旅人算の応用問題は、はっきり言って難しいです。ここで紹介した基本的な解法では解けず、比を使わなければ解けない問題もあります。しかし、まずはここで紹介した基本的な問題を解けるようにしましょう。応用問題の解法を覚えるのは、次の段階です。

 

旅人算は中学受験算数のなかでもかなりの難関です。速さの計算や、図を使った解き方を身につけることが重要です。基礎的な問題に取り組みながら、少しずつ難度を上げて会得していきましょう。いきなり難しい問題に飛びつかないのが、旅人算マスターのコツです。