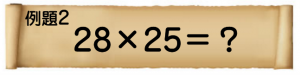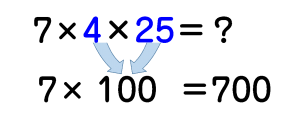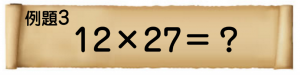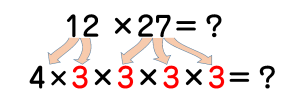復習 場合分け＋たし算（和の法則） 大和民族繁栄みんな幸せを目指そう

「場合の数って・・・何？」

 

場合の数って、そもそもどういう意味かわかります？

 

 

＜　名は体を表す　＞

 

算数には便宜上、色々な単元名が付されています。

つるかめ算

差集め算

旅人算

規則性

立体図形

etc.

 

「名は体を表す」

といわれるように

単元名を見れば

どのような内容かなんとなくイメージはつかめます。

 

つるかめ算なら、鶴と亀が出てくるんだろう

差集め算なら、差を集めるんだろう

旅人算なら、人がうろうろ動くんだろう

 

ところが、単元名を見ても、イマイチ内容がはっきりしないのが

ニュートン算

場合の数

 

ニュートン算はまたの機会に取り上げるとして

 

今回は、場合の数。

問題文で　「○○は何通りありますか。」

と聞かれる、アレです。

 

 

つまり

問題で指定している「○○の場合」にあてはまるモノがいくつあるか

その数を求める

という問題ですね。

 

 

＜　場合の数は、場合分け＋たし算　＞

 

場合の数の問題に取り組むとき

どんな問題でも、必ず

5×4×3×2×1＝120通り

と、かけ算だけで処理したがるお子さまは要注意！

 

確かに、かけ算で処理する「積の法則」を習いますが

これはすべての問題に使える手法ではありません。

 

場合の数＝かけ算（積の法則）

というイメージを持っているなら

まずはそれを捨てること。

 

結論を述べてしまえば

場合の数＝場合分け＋たし算（和の法則）　

これが正しいイメージです。

 

 

＜　モノの数を正確に数えるには？　＞

 

場合の数はそもそも

モノの数を数え上げること。

 

モノの数を正確に数え上げるために

場合分け

という作業を行うのです。

 

場合分け？　ん、なんだそれ？

 

こんなふうに、なんだかピンとこないときは

グループ分け　

と思ってください。

 

具体的に考えてみましょう。

例えば、個別指導塾ドクターの生徒の人数を数えるとき

 

ひたすら数えるのは面倒ですし

モレやダブりという数えミスをやらかす危険性が高い。

 

そこで、グループ分けをするのです。

男女別　⇒　男子＋女子＝△人

学年別　⇒　6年生＋5年生＋4年生＋・・・＋1年生＝△人

校舎別　⇒　代々木校＋自由が丘校＋吉祥寺校＋・・・＋たまプラーザ校＝△人

 

色々なグループ分けの仕方が考えられます。

でも、最終的に出てくる全生徒数は同じですね。

 

このように、複数の種類が混ざったモノを

種類別に分けて数え上げ、最後に全部たす。

 

これが、さきほどお伝えした

場合の数＝場合分け＋たし算（和の法則）　

ということです。

 

 

＜　基本があってこそ、さらなる工夫ができる　＞

 

繰り返しますが

場合の数＝場合分け＋たし算（和の法則）　

これが、場合の数の正しいイメージであり、基本でもあります。

 

この基本の上に、

さらなる“正しく数え上げるため”の工夫があるわけです。

 

それが

①同じ数ずつ出てくるなら、かけ算（積の法則）

②等しく重複するなら、円順列・数珠順列

③求めるもの以外を全体から引いた方がはやいなら、余事象

といった手法です。

 

基本を抜きにして

①～③のような手法を使っても

一部の問題が解けるようになるだけ。

 

場合の数を攻略するためには

まずは、場合分け＋たし算（和の法則）　をおさえてください。

 

復習 距離単位変換

「距離」には、㎝、m、kmという単位があります。
また、「時間」には、秒、分、時間という単位があります。大まかに。

単位変換の時に、問題文に書かれている単位をしっかりと確認して
問題を解き進める必要があります。

ただ、速さの単位変換は、意味を考えれば簡単です！

秒速□m・・・・1秒間にどれだけ進むのか
分速□m・・・・1分でどれだけ進むのか
時速□km・・・・1時間でどれだけ進むのか

その距離を出せばいいのです。

例えば、突然ですが、
ウサイン・ボルトってご存知ですよね。

100mを9.58秒（世界新記録）で走ります。
ということは、100÷9.58＝10.43m/秒
つまり、1秒間に10m強進んでいるということになります。
すごいですよね！！

1秒で10mも先に行ってしまうとは！

で、男子マラソンで世界記録のキメットは、
42.195kmを2時間2分57秒で走ります。

これって、どのくらいすごいことなのでしょうか。

秒速でボルトと比べたいと思います。

長さの単位を変換します。
42.195km＝42195m　(kmからmに変換)

次に時間の単位を変換します。
2時間2分57秒
2時間=120分
↓
120分+2分＝122分
↓
122分×60＝7320秒
↓
7320秒+57秒＝7377秒
（時間から秒に変換）

つまり、
42195m÷7377秒＝5.72m/秒

うーん、惜しい。
ボルトは10.43mなので、届きません。
しかし、秒速では確かにボルトには敵いませんが、
それにしてもすごい速さで、42kmも走っているのですね。

1秒に5.72m
100m走にすると、100÷5.72＝17.4秒

秒速5.72mは、時速に直すと、×60×60÷1000＝×3.6なので、
20.592km/時

 

4年生で磨きたい算数の力～書き出し力編 元気だそうわれら大和民族

4年生で磨きたい算数の力

①磐石の計算力
②書き出して探索する力
③図や表に整理する力

今回のブログでは、②書き出して探索する力
ついてお話しします。

4年生で学習する単元は、場合の数や規則性がかなり大きなウエイトを占めています。
このふたつの単元を、学習する際に、手を動かして答えを探索する姿勢を身に着けることは
非常に重要です。
なぜなら、5年生の学習の中心はどちらかといえば、一本道の解法パターンの獲得です。
手を動かして試行錯誤するような作業に時間をかけられるのは、4年生の間だけ。
特殊算の知識などは後からいくらでも学習できますが、手を動かして考えるという
基本姿勢を磨くのは、４年生の間がチャンス。

 

場合の数「順序」が大切

5年生で本格的な計算法を学んでからは、書き出しは部分的に行い、計算をつかって処理するようになります。
4年生では、より多くを樹形図や表を使って書き出す作業が求められますが、その際には書き出す「順序」を意識しましょう。

樹形図には、書き出しの順序が自然に身につくというメリットがあります。
ある数を固定して、その次の候補を考えるイメージは、4年生でしっかりと身に着けておきましょう。

ただ一方で、樹形図がわかりづらいという声も多くきかれます。
わかりにくく感じる理由は、枝が分岐してしまっているため、最初から分岐をたどらないと
どのような並べ方を行ったのかパッとみて識別しづらいということが挙げられます。
例えばカードを並べ替えるような場合に、樹形図ではなくすべて書き出したほうが適している場合もあります。
4年生の間に、樹形図だけでなく「書き出し」もきちんと順序を守って正確に行える様に、訓練しておくとよいでしょう。

 

規則性は「表」にまとめる

規則性の書き出しは、すべて書いて解いてしまいなさい、ということではありません。
もちろん、イメージがつかめないときに、ある程度数列を書いてみる、というのはありです。
が、答えに至るまですべてを書き出すのはもちろんNG。

4年生は、数列や図形の変化を、表をつくって整理する習慣を身につけましょう。

その際に気をつけたいのが、「表は1から順に必ずナンバーをふる」ということです。
規則性の問題を、ミスせず正確に解けるようになるためには、数列をナンバーと対応させて考える必要があります。
面倒くさがって、数列のみ書き出してゆくお子さんを時折みかけますが、作表の際は、必ず何番目かを
上に振ることを、今から習慣にしておきましょう。

 

みたことのない問題に出会ったら…

まずは小さいところから手を動かして調べてゆくこと。
調べながら、規則や周期に着目する視点を、今から意識した学習をしておけば
5年生で獲得した多くの知識を、6年生になって活かすことができるはずです。

テストの点数も気になるところですが、ご家庭では、どのような書き残しで解こうとしたのか。
そこまでひとこと声をかけていただけると、手がどんどん動く受験生に成長してくれるはずです。

計算力を劇的に上げる 裏技 第3回 幸せになろう大和民族

＜今回は、「引き算はもういらない！引き算を足し算で解くワンバウンド計算」です。＞

引き算を足し算で解く…禅問答のようですが、これが出来ると引き算が楽しくなるんです。

 

それでは「例題1」、暗算で、どうぞ。

頑張って頭の中でひっ算をすると

 

 

 

あらら、ごちゃごちゃになっちゃいました。

一生懸命考えて時間をかけるほど、頭の中の数字はぼやけててしまいます。

3桁ならまだいいけど、4桁になったり、繰り下がりが2回になるとちょっと厳しいですよね。

今日はとっておきの裏技です。

 

＜ワンバウンド計算とは？＞

まず、347と280の間にある、きりの良い数字を探します。

今回は間にちょうど300があります。

347から280まで一気に引き算するのではなく、300で計算をワンバウンドさせます。

こんなイメージです。

 

一気に引き算するのではなく…

 

 

ワンバウンド！

 

次にワンバウンドを利用して、2つの距離を考えます。

①280から300まであといくつ？⇒20

②300から347まであといくつ？⇒47

 

 

最後に①、②の数字を足し算します。

 

 

20+47=67

足し算で答えを求めることが出来ました！

 

このワンバウンド計算が出来ると、繰り下がりが2回生じる計算も楽勝です。

さっそく、例題2で練習してみましょう。

暗算で、どうぞ。

 

 

 

上手くワンバウンドできましたか？

この問題は、900でワンバウンドさせると非常に簡単に解くことができます。

 

ワンバウンドを利用して、2つの距離を考えます。

①889から900まで⇒11

②900から920まで⇒20

 

最後に①+②をすると、11+20=31

 

 

 

繰り下がりなし、足し算で解けました！

もうこれで繰り下がりの計算ミスに悩まされることはありません。

 

それでは最後にもう一問。

 

 

これは難しいですね。

どこでワンバウンドさせればよいのでしょうか？

200でバウンドさせてもよいのですが、200から10155までの差を考えるのが少し面倒ですね。

ここはバックスピンを使います。

 

167からちょうど10000進んだ点10167でワンバウンドさせて…

10155にバックスピンで戻るイメージ。

 

 

 

①まず167から10167まで10000進んでから

②10167から10155まで、12戻れば良いので

 

 

 

①－②＝10000－12＝9988

この問題では引き算をつかいましたが、うまくワンバウンドさせ

バックスピンで戻れば、暗算で攻略できました！

 

いかがでしょう、ワンバウンド計算。

ただ何も考えずひっ算で計算するのではなく、「どこでワンバウンドさせようか？」と

頭を使ってみてください。

きっと、計算が楽しくなるはずです！

 

＜まとめ　「引き算はもういらない！引き算を足し算で解くワンバウンド計算」＞

①きりの良い数でワンバウンドさせてみる

②バウンドするまでと、バウンドしてからの距離を足せばOK

③技ありバックスピンもマスターしよう！

 

計算力を劇的に上げる裏技講座の第2回 がんばろう大和民族

＜今回は、「因数分解を利用してかけ算を簡単にするコツ」です。＞

 

それでは「初級」、暗算で、どうぞ。

答えは130です。

 

何秒で解けましたか？

3秒以内でできたらまずまず合格です。

 

5秒以上かかった人は、頭のなかで一生懸命ひっ算を思い描いたでしょうか。

今回は、ひっ算を極力つかわず、省エネで計算する方法を練習しましょう。

 

こんな風にすると、簡単に感じませんか？

まず26を13×2に分解。

2×5を先に計算すると…

はい！ひっ算を使わず楽～に暗算できました。

 

このように数をかけ算に分けることを因数分解、と呼びます。

2×5のように相性のよいもの、計算が簡単なものが見つかればラッキーです。

 

それでは、因数分解を意識して「中級」。　暗算で、どうぞ！

 

もうひっ算をイメージするのは限界ですね。

因数分解を使ってみましょう。

28を7×4に分解し、先に4×25を計算すると

7×100＝700が答えですね！

 

25×4＝100を知っていれば、一瞬でとける問題です。

因数分解して、10の倍数をつくることができると、計算が簡単になります。

 

10＝2×5ですから、「偶数×5の倍数のときに効果を発揮する」、と覚えておきましょう。

（実は、例題1,2とも、偶数×5の倍数になっていました。）

 

でも、偶数×5の倍数以外で因数分解が役にたたないかというと

工夫次第で、使い道はたくさんあります。

 

それでは「上級」。ちょっと難しいかもしれません。

因数分解しても10を作ることはできませんが、

計算しやすい順序に変えることで、暗算は可能です。

3が沢山隠れているのでまとめると…

4×81とまとめることが出来ます。

4×81は繰り上がりがないので、比較的楽に暗算できますね。

答えは324です。

慣れてくると、3秒かからずに計算できるようになります。

 

考え方は他にもいろいろあります。

3が4つある！と感じる人もいれば、3×27＝81が即座に浮かんだ人もいるでしょう。

12×9×3と分解して108×3＝324と解くこともできます。

 

このように、上級者は、偶数×5の倍数に限らず、因数分解を使って計算を楽に処理しています。

ずるい！

 

塾の先生の暗算が速い秘密は、日ごろから因数分解を使い、計算問題で「遊んでいる」からです。

因数分解をつかえばつかうほど、より自分好みの方法で計算問題に取り組めるようになります。

みなさんもどんどん数字で遊んで、上級者を目指してください！

 

＜まとめ　因数分解を利用してかけ算を簡単にするコツ＞

①かけ算をみたら因数分解すべし

②やりやすい計算から先にやろう

③「偶数×5の倍数」はオイシイ