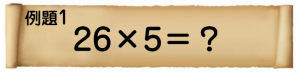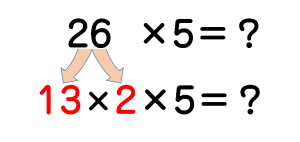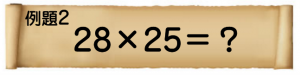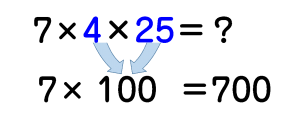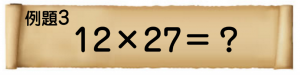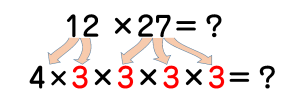<今回は、「因数分解を利用してかけ算を簡単にするコツ」です。
それでは「初級」、暗算で、どうぞ。
答えは130です。
何秒で解けましたか?
3秒以内でできたらまずまず合格です。
5秒以上かかった人は、
今回は、ひっ算を極力つかわず、
こんな風にすると、簡単に感じませんか?
まず26を13×2に分解。
2×5を先に計算すると…
はい!ひっ算を使わず楽~に暗算できました。
このように数をかけ算に分けることを因数分解、と呼びます。
2×5のように相性のよいもの、
それでは、因数分解を意識して「中級」。 暗算で、どうぞ!
もうひっ算をイメージするのは限界ですね。
因数分解を使ってみましょう。
28を7×4に分解し、先に4×25を計算すると
7×100=700が答えですね!
25×4=100を知っていれば、一瞬でとける問題です。
因数分解して、10の倍数をつくることができると、
10=2×5ですから、「偶数×5の倍数のときに効果を発揮する
(実は、例題1,2とも、偶数×5の倍数になっていました。)
でも、偶数×5の倍数以外で因数分解が役にたたないかというと
工夫次第で、使い道はたくさんあります。
それでは「上級」。ちょっと難しいかもしれません。
因数分解しても10を作ることはできませんが、
計算しやすい順序に変えることで、暗算は可能です。
3が沢山隠れているのでまとめると…
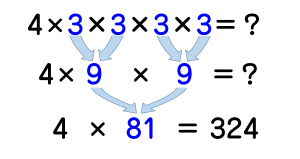
4×81とまとめることが出来ます。
4×81は繰り上がりがないので、比較的楽に暗算できますね。
答えは324です。
慣れてくると、3秒かからずに計算できるようになります。
考え方は他にもいろいろあります。
3が4つある!と感じる人もいれば、3×27=
12×9×3と分解して108×3=
このように、上級者は、偶数×5の倍数に限らず、因数分解を使っ
ずるい!
塾の先生の暗算が速い秘密は、日ごろから因数分解を使い、
因数分解をつかえばつかうほど、
みなさんもどんどん数字で遊んで、上級者を目指してください!
<まとめ 因数分解を利用してかけ算を簡単にするコツ>
①かけ算をみたら因数分解すべし
②やりやすい計算から先にやろう
③「偶数×5の倍数」はオイシイ