 ニュートン算とは
ニュートン算とは
ニュートン算は仕事算の応用的な問題ですが、仕事算とは、「ある一定の仕事を与えられた時、それを終える時間を求める問題」です。
主に「仕事を処理するスピードが異なる人が複数で一緒に行った際の時間」や、「人数が異なる際にかかる時間の違い」などを求める問題が多いです。
仕事算の例
ある与えられた仕事を終えるのに3人なら6時間かかる場合、5人なら何時間何分で終えられるか。
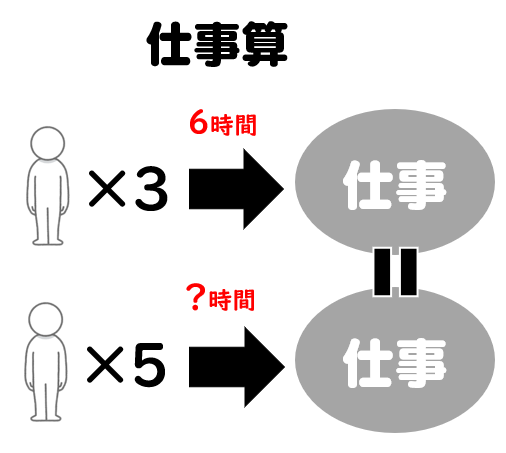
仕事量が不明なので、まずは「仕事=書類作成18枚」など、計算しやすい値で定義してあげるのがポイントでした。解き方についてはこちらに詳しく解説しています。
これに対しニュートン算は、時間とともにやるべき仕事が増えていきます。
ニュートン算の例
最初に与えられた仕事に加え、時間ととも一定の量だけ増えていく仕事をすべてすませるのに3人なら6時間、5人なら2時間かかる。では4人なら何時間かかるか。

仕事算に比べて不明な値が多く、情報量も多いため、解き方を知らなければ何からすればいいのか悩んでしまうでしょう。
他にも「人」と「仕事」をそれぞれ「牛」と「草」に置き換えて『牛が草を食べ終わる時間を求める問題』

『水が湧き出る井戸の中をポンプで空にするのにかかる時間』や『チケット売り場に並ぶ人すべてをさばき切る時間』など、様々なパターンがあります。
ではニュートン算の解き方について解説していきます。
ニュートン算の解き方
では上で示した例題を使ってニュートン算の解き方を解説していきます。
ニュートン算の例
最初に与えられた仕事に加え、時間ととも一定の量だけ増えていく仕事をすべてすませるのに3人なら6時間、5人なら2時間かかる。では4人なら何時間かかるか。
ニュートン算でも仕事算と同様、仕事量がわからないのが厄介なので、まずは計算しやすいように仕事量を定義します。
この問題ではすべての人が同じスピードで仕事をこなすので、1人が1時間でこなす仕事を「1」と定義しましょう。より具体的に考えるために「1枚の書類作成」とします。

このように定義すると、3人で6時間働けば3×6=183×6=18で18枚の書類が、5人で2時間働けば5×2=105×2=10で10枚の書類が作成できることが分かります。
そしてこれらとともに、問題文の情報を数直線にまとめます。

最初に与えられた仕事はどちらも同じなので、「18枚」と「10枚」という両者の仕事量の差は、時間とともに増えた仕事量によるものです。

4時間(6時間-2時間)で8枚(18枚-10枚)の書類が増えたので、1時間で増える仕事量は8÷4=28÷4=2で「2枚の書類作成」です。
ここから、6時間で増える仕事量は2×6=122×6=12より「12枚の書類作成」というのが分かるので、最初に与えられた仕事は18−12=618−12=6で「6枚の書類作成」というのが分かります。

では4人で仕事をする場合について考えてみましょう。
最初に書類作成×6の仕事が与えられ、1時間で4枚の書類が作成できますが、作成しないといけない書類は1時間で2枚ずつ増えていきます。

増える仕事量と減る仕事量の差し引きを考えると、最初の6の仕事が1時間で2ずつ減っていくので、6÷2=36÷2=3で4人だと3時間後にすべての仕事が終えられることが分かりました。
以上がニュートン算の問題の解き方です。
はじめは仕事算と同じように仕事量を定義することからはじまりますが、最後は増減する仕事量から単位時間あたりの変化に着目するので、この部分は「追いつき旅人算」と考え方が同じです。
たえば、以下のような問題。
Aくんが分速100m100mで家を出発した55分後に、Bくんがそれを追いかけて分速150m150mで家を出たら何分後に追いつくか。
移動している人を追いかける場合にかかる時間は、それぞれの速さから単位時間あたりの変化を考えましたね。

ニュートン算は『仕事算』+『追いつき旅人算』の問題なので、これらの問題が解けないならニュートン算も解けないでしょう。まずは仕事算と旅人算をしっかりと抑えた上でニュートン算にチャレンジするのをオススメします。
 ニュートン算とは
ニュートン算とは

























