円と正多角形 家長のお父さんが家族を守る

今回は「円と正多角形」をテーマに平面図形のトレーニングについてお話いたします。
たとえば、次の正六角形とおうぎ形を組み合わせた図を見てください。

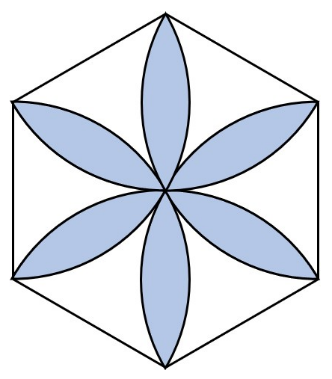
問題は「色を付けた部分のまわりの長さは何cmか」です。

正六角形の1辺の長さは6cm、円周率は3.14としましょう。
円のまわりの長さの学習が済んでいない学年のお子さんは円何周分の長さか考えてもらってもかまいません。

この図の様子を見抜けた人は多いかもしれませんね。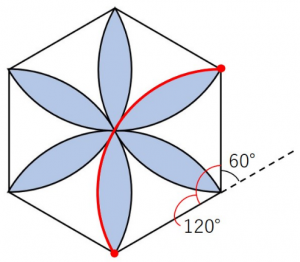

半径6cm、中心角120度のおうぎ形の弧が6本ありますので、
6 × 2 × 3.14 ×  × 6 ＝ 75.36
より、75.36cmとなります。

6つのおうぎ形を合わせると720度分になるので、円2周分と考えられれば問題ありません。

さて、次の図はどうでしょうか？
正五角形とおうぎ形を組み合わせた図です。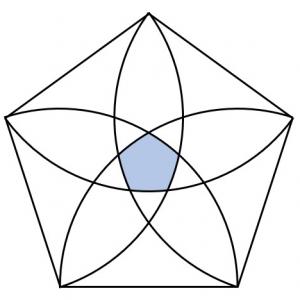

こちらの図についても、正五角形の1辺の長さを6cmとして、色を付けた部分のまわりの長さは何cmか考えてみましょう。

先ほどの図よりも細かく考える必要が出てきました。

この問題をふまえて、今後どのようにトレーニングをすると効果的か、先にお伝えします。
「図形はセンス」と一刀両断されてしまうことがありますが、問題を解く上ではセンスより知識の方が重要です。なかなか問題が解けないからといって、闇雲に練習量を増やしても問題を解く上で重要な着眼点は見えてきません。

まずは、図形の性質を知識としてしっかりと押さえましょう！
今回であれば、鍵を握っているのは、

①円やおうぎ形⇒半径を2本使って三角形をつくると二等辺三角形になる。
②正多角形⇒外角の和は360度なので、１つの内角は180−360÷（角の個数）で求められる。

という、２つの知識です。
全体を形作っている基本図形がおうぎ形と正多角形ですので、それに関する知識を使おうという姿勢で図を観察しましょう。その知識が使える部分を見つけたら、具体的な計算を進めて答えの数値を求めましょう。
答えまでの道筋が一気に見えるときもあれば、少しずつ特徴が生かされて答えにたどり着く場合もあります。

１．各図形の性質や特徴を知識として身に着ける。
２．身に着けた知識を使える部分はないか観察する。
３．使える部分を見つけたら、知識にしたがって計算を進める。

この３つのステップが問題の解き方およびトレーニング手順となりますが、せっかく知識をもっているのに、それを使える部分を探すという観察するときの姿勢が抜けてしまっている人が多いように思えます。

さて、先ほどの図について具体的に考えてみましょう。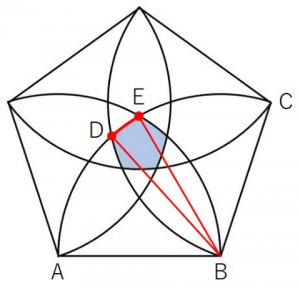

求める長さは弧DE５つ分の長さとなりますが、その長さを求めるために中心角にあたる角DBEの大きさが必要になります。この角の大きさを考えることが解答までの大筋になります。

知識を使うという姿勢で観察していると、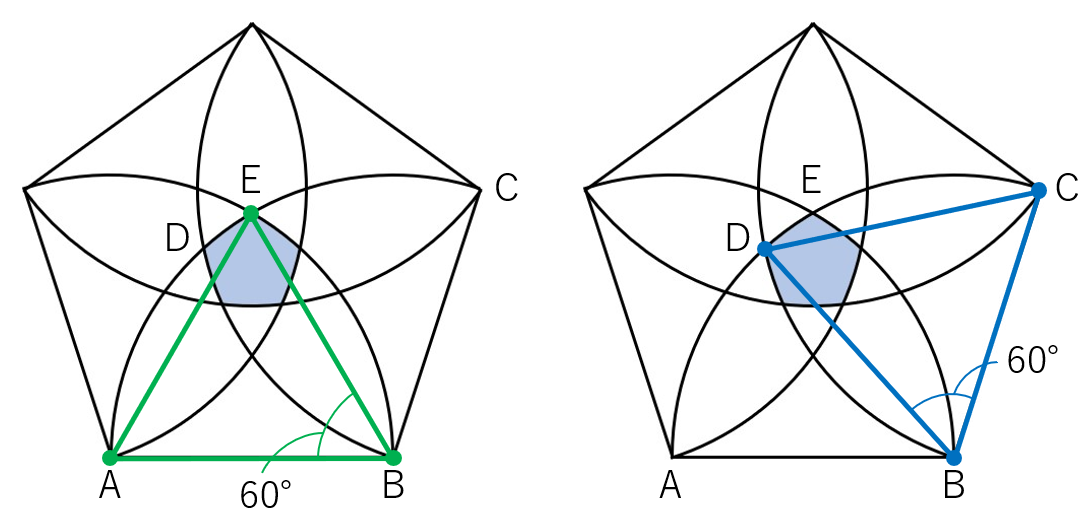次のような特徴が見えてきます。

今回は3辺の長さが等しくなるため、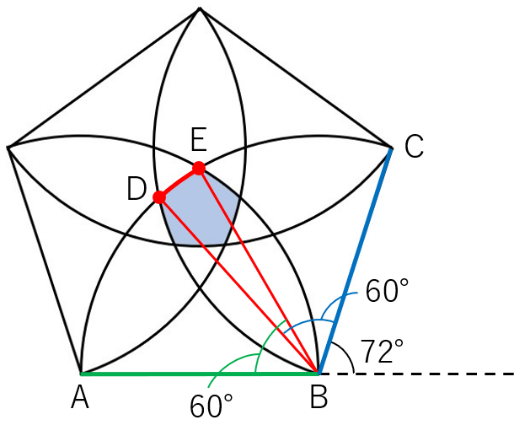三角形ABEと三角形BCDが、二等辺三角形からさらに発展して正三角形となることが見えてきますね！正三角形の1つの角の大きさは60度ですので、このことをもとの図形にあてはめると、

ちょうど、2つの60度の角が重なった部分が角DBEの大きさといえます。
ここで、正五角形の１つの外角の大きさは360÷5＝72より72度ですので、
1つの内角の大きさは180−72=108より、108度です。

さあ、ここまで来ればあと一歩です。

角ABDの大きさは、角ABC－角DBC＝108－60＝48より48度
よって角DBEの大きさは、角ABE－角ABD＝60－48＝12より12度です。

最後に解答は、
6 × 2 × 3.14 ×  × 5 ＝ 6.28
より、6.28cmとなります。
または、12×5＝60より、60度分の長さにあたると考えるとこができれば大丈夫です。

もとになる正多角形の角の個数が変わっても使用する知識は同じですので、同じように「知識を使う」という姿勢で問題を見るトレーニングを積みましょう。その他の図形の問題も、基本的なトレーニング方法は同じですが、またの機会にお話しいたします。

目指せ、図形マスター！
それでは、またお会いしましょう！